新的最优非对称量子纠错码的构造
2023-03-08孙麒麟王立启
孙麒麟, 王立启
(合肥工业大学 数学学院,安徽 合肥 230601)
0 引 言
文献[1]给出了利用经典纠错码构造非对称量子纠错码的CSS构造法,并指出研究非对称量子纠错码的重要性,但没给出非对称的本质;文献[2]通过物理实验证明,量子比特翻转错误比量子相位翻转错误发生的概率大很多,由此引发了人们对非对称信道中的量子纠错码研究。学者们通过各种方法设计构造高性能的非对称量子纠错码,特别是LDPC码和BCH码被广泛应用于非对称量子纠错码的构造[3-5];文献[6]利用代数几何码构造非对称量子纠错码,并得到了一些参数较好的非对称量子纠错码;文献[7]在F4上迹厄米特内积意义下,给出了加性码构造非对称量子纠错码的通用方法。此后,各种类型的新的非对称量子纠错码被构造出来[8-10]。文献[11]利用经典的负循环码构造了2类最优的非对称量子纠错码;文献[12]和文献[13]分别利用经典的常循环码构造了6类和2类最优的非对称量子纠错码;文献[14]利用经典的常循环码构造了2类长为(q2+1)/5的最优非对称量子纠错码;文献[15]利用准循环码构造了一些最优的非对称量子纠错码;文献[16]利用经典的常循环码构造了几类长为n=(q2+1)/a的新的量子MDS码。
受上述工作启发,本文通过Fq2上的常循环码构造了2类长为n=(q2+1)/a的新的最优非对称量子纠错码,其中q为奇素数的方幂,a=(m2+1)/2,m≥3为奇数。
1 基础知识
设Fq2是含有q2个元素的有限域,其中q是素数的方幂。给定任意向量
x=(x0,x1,…,xn-1),
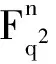
其厄米特内积定义为:

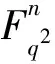
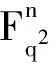
若Fq2上长为n的线性码C满足C⊆C⊥H,则称C为厄米特自正交码。
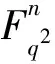
引理1(Singleton界)[17]设C是Fq2上的[n,k,d]线性码,则k≤n-d+1;特别地,若等号成立,则称其为MDS码。
容易验证,Fq2上η-常循环码的厄米特对偶码C⊥H是η-q-常循环码。设ω是Fq2中的本原元。假定gcd(n,q)=1,取η=ωq-1,从而有ηηq=1,因此,Fq2上η-常循环码的厄米特对偶码C⊥H是η-常循环码。η-常循环码存在确定其距离的BCH界。
引理2(常循环码的BCH界)[18]假设gcd(q,n)=1,设C=〈g(x)〉是Fq2上长为n且g(x)的根为{δ1+ir|0≤i≤d-2}的η-常循环码,其中δ是rn次本原单位根,则C的极小距离至少为d。
记Ω={1+ir|0≤i≤n-1},对于任意的j∈Ω,令Cj是包含j的模rn的分圆陪集,则mi(x)=Πh∈Cj(x-δh)是xn-η在Fq2上的首一不可约因子。每一个Cj对应xn-η在Fq2上的一个不可约因子。设C是Fq2上由多项式g(x)生成的长为n的η-常循环码,则集合Z={j∈Ω|g(δj)=0}称为C的定义集。显然C的定义集是模rn的q2-分圆陪集的并集,且dim(C)=n-|Z|。
下面给出非对称量子纠错码的定义和相关性质。

对于一个参数为[[n,k2,dz/dx]]q2的CSS非对称量子纠错码,其参数n、k、dz和dx之间的关系有下面的结论。
定理2[4]若存在一个参数为[[n,k2,dz/dx]]q2的CSS非对称量子纠错码Q,则Q满足非对称量子Singleton界,具体为:
k≤n-dz-dx+2。
特别地,当k=n-dz-dx+2时,称Q为最优码或非对称量子MDS码。
2 最优非对称量子纠错码的构造
本文将利用经典的常循环码构造2类长度为n=(q2+1)/a的最优非对称量子纠错码,其中q为奇素数的方幂,a=(m2+1)/2,m≥3为奇数,易知此时a|(q+m)或a|(q-m)。以下分这2种情形进行讨论。
2.1 最优非对称量子纠错码的构造Ⅰ
本节讨论当a|(q+m)时,最优非对称量子纠错码的构造,先给出一个重要的引理。

定理3 设q是奇素数的方幂,a|(q+m),a=(m2+1)/2,m≥3为奇数,n=(q2+1)/a,则存在参数为[[n,n-2(s+t+1),(2s+2)/(2t+2)]]q2的非对称量子纠错码,其中s、t为正整数,且0≤t≤s≤(mq-1)/2a-1。

{k-(q+1)t,…,k-(q+1),k,k+(q+1),
…,k+(q+1)t},
由引理1知,C2的极小距离至少为2t+2。根据引理2可得,C2的极小距离为2t+2。因此,C2是参数为[n,n-(2t+2),2t+2]q2的q2-元ωq-1-常循环码。

定理3中的非对称量子纠错码满足dz+dx=2s+2t+4=n-k+2。由定理2可知,参数为[[n,n-2(s+t+1),(2s+2)/(2t+2)]]q2的非对称量子纠错码达到非对称量子纠错码的Singleton界。因此这些非对称量子码是最优的。
例1 设m=5,q=31,则n=74。假设ω30-常循环码C1的定义集为Z1=C481={481},则C1是参数为[74,73,2]961的MDS码。假设ω30-常循环C2的定义集为:
Z2=C481∪C449∪C417∪C385∪C353∪
C321∪C289∪C257=
{481,289,321,353,385,417,449,
481,513,609,641,673,705},
则C2是参数为[74,59,16]961的MDS码。由定理3可知,存在参数为[[74,58,16/2]]961的最优非对称量子纠错码。通过赋予C1和C2不同的定义集,得到最优非对称量子纠错码,见表1所列。

表1 长为74的961元最优非对称量子纠错码
2.2 最优非对称量子纠错码的构造Ⅱ
本节讨论当a|(q-m)时,最优非对称量子纠错码的构造,先给出一个重要的引理。

类似定理3的讨论,可得如下结论。
定理4 设q是奇素数的方幂,a|(q-m),a=(m2+1)/2,其中m≥3为奇数。设n=(q2+1)/a,则存在参数为[[n,n-2(s+t+1),(2s+2)/(2t+2)]]q2的非对称量子纠错码,其中s,t为正整数,且0≤t≤s≤(mq+1)/2a-1。
定理4中的非对称量子纠错码满足
dz+dx=2s+2t+4=n-k+2。
由定理2可知,参数为[[n,n-2(s+t+1),(2s+2)/(2t+2)]]q2的非对称量子纠错码达到非对称量子纠错码的Singleton界,因此这些非对称量子纠错码是最优的。
例2 设m=7,q=57,则n=74。假设ω56-常循环码C1的定义集为Z1=C1 625={1 625},则C1是参数为[130,129,2]3 429的MDS码。假设ω56-常循环码C2的定义集为:
Z2=C1 625∪C1 567∪C1 509∪C1 451∪C1 393∪
C1 335∪C1 227∪C1 219=
{1 219,1 227,1 335,1 393,1 451,1 509,1 567,
1 625,1 683,1 741,1 799,1 857,1 915,1 973,2 031},
则C2是参数为[130,115,16]3 429的MDS码。由定理4知,存在参数为[[130,114,16/2]]3 429的最优非对称量子码。通过赋予C1和C2不同的定义集,得到最优非对称量子纠错码,见表2所列。

表2 长为130的3 249元最优非对称量子纠错码
3 结 论
本文利用有限域上Fq2上的经典常循环码构造了2类长为n=(q2+1)/a的最优非对称量子纠错码,其中q为奇素数的方幂,a=(m2+1)/2,m≥3为奇数。具体如下。
(1)当a|(q+m)时,存在参数为[[n,n-2(s+t+1),(2s+2)/(2t+2)]]q2的最优非对称量子纠错码,其中0≤t≤s≤(mq-1)/2a-1,s、t均为正整数。
(2)当a|(q-m)时,存在参数为[[n,n-2(s+t+1),(2s+2)/(2t+2)]]q2的最优非对称量子纠错码,其中0≤t≤s≤(mq+1)/2a-1,s、t均为正整数。
