棉氨混纺织物纤维含量测定的不确定度评定

娄 亿，王佳云，肖 雁，茅沈杰

（江苏省纺织产品质量监督检验研究院，江苏 南京 210007）

测量不确定度简称不确定度，根据所用的信息，表征赋予被测值分散性的非负参数[1]。纺织品纤维含量分析是纺织品检验的重要项目，国家标准GB/T 29862—2013《纺织品 纤维含量的标识》对混纺产品的纤维含量允差有明确规定[2]。为满足检测工作的需要以及客户的要求，尤其需要监督抽查纤维含量检测结果的判定过程。纺织品纤维含量二组分混纺比的测量是一种间接测量，在测量过程中，引起测量不确定度的因素较多。测量系统的概念不局限于测量仪器、测量设备，还有对测量赋值的人、机、料、法、环等因素的综合考量[3]。实验室对每一项有数值要求的测量结果都要进行测量不确定度评估。

纺织品纤维含量是指组成纺织产品面料的纤维类别以及每种纤维的质量比例，以某种纤维的量占产品或产品某部分纤维总量的质量百分率表示。纤维含量是决定纺织产品使用性能的重要指标，纺织产品的耐久性、穿着舒适性、保暖性、外观保持性等都与纤维含量密切相关。因此，消费者选购纺织产品时，产品明示的纤维含量是比较重要的参考依据之一[4]。严格控制纺织品纤维含量，保证产品质量，通过不确定度分析和处理结果具有非常重要的意义。本实验以棉氨混纺织物为例，分析测量不确定度的来源，对测量结果的不确定度进行评定。

1 实验方法

1.1 检验原理

对于已鉴别出纤维组分的纺织品，采取适当的方法去除非纤维物质后，采用手拆分解的方法分解纺织品中不同种类的纤维，并对纤维进行干燥、冷却、称重，计算每一种纤维的质量分数[5]。

1.2 实验仪器

AL204电子分析天平（最小示值为0.1 mg，最大量程为220 g，标准证书的称量误差为0.1 mg，梅特勒-托利多仪器有限公司），YG747恒温烘箱（南通宏大实验仪器有限公司）。

1.3 检测过程数学模型

由GB/T 2910.1－2009附录B可知，纤维净干质量分数计算公式如下：

式中：P1、P2分别为第一组分、第二组分净干质量分数，%；m1、m2分别为第一组分、第二组分净干质量，g。

1.4 不确定度

1.4.1 不确定度的含义

不确定度是指实际检测过程中存在的对测量结果不能绝对肯定的程度，反映了测量误差的存在原因，同时也代表着测量数据结果的可信程度，是评价测量结果质量的重要指标[6]。测量结果与被测量的真实值越接近，不确定度越小，数据的可靠性就越高，准确度高；反之，不确定度越大，测量结果的质量越低，数据的可靠性低，准确度不高。

1.4.2 不确定度的来源

本研究采用手工分解法测试纤维含量，测试程序：产品含量定性分析→对试样预处理→制备定量测试样品→手拆法分解处理→纤维各组分称重→代入公式计算结果。

通过数学模型和经验分析，测试结果的不确定度来源主要如下：操作过程的重复性引入的不确定度，包括试样的代表性、操作人员预处理、取样拆分等；测量样品质量时由天平引入的不确定度；数据修约、d值和纤维公定回潮率等可能导致的不确定度等[7]。

1.4.3 不确定度分类

（1）A类不确定度。对在标准规定测量条件下测得的数值用分析统计的方法评定测量不确定度分量，用Ua来表示[8]。

（2）B类不确定度。采用不同于测量不确定度A类评定的方法评定测量不确定度分量，通过实验的方法或者其他信息来估计，有主观鉴别纤维的成分，用Ub表示。

（3）合成标准不确定度，是由在一个测量模型中各输入量的标准测量不确定度得到的输出量的标准测量不确定度。合成标准不确定度的自由度称为有效自由度，表明所评定的合成标准不确定度的有效程度，用Uc表示。

（4）扩展不确定度。表述校准检测能力时，通常没有测量结果，而是仅给出测量设备的扩展不确定度。其中当然不包含被校准测量仪的示值重复性，用U表示。

2 测量不确定度的评定分析

2.1 A类不确定度评定分析

当纤维含量需要做不确定度评估时，通过公式（3）（4）可以看出，检测多份试样可以提高结果的准确性[9-10]。因此，做不确定度评估时，应检测多份试样。可以用统计方法评定不确定度分量，即A类分量。

对同一块棉/氨纶包芯牛仔服装面料随机取一组10个样品，按照标准要求测量各组分的纤维含量，结果如表1所示。

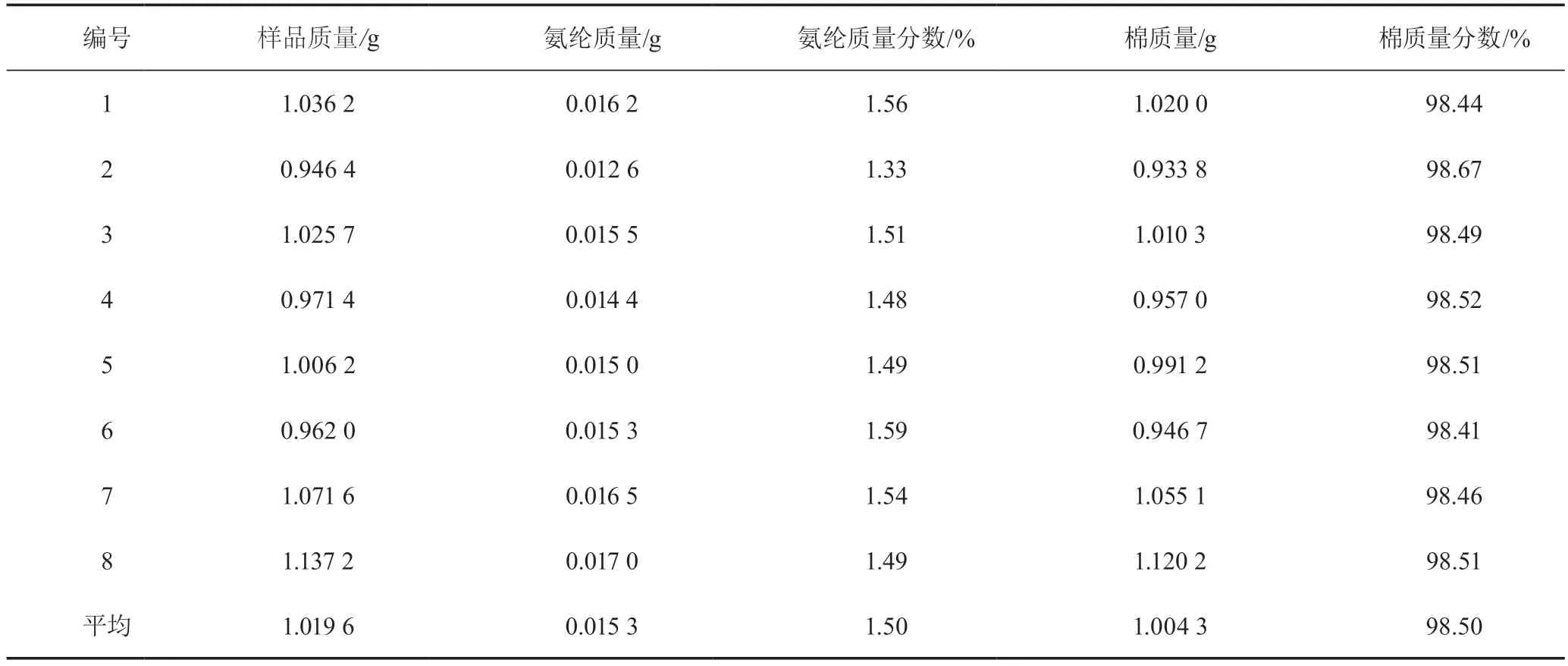
表1 棉氨手工拆分各组分的纤维净干质量分数

式中：n为测量次数；v为自由度，等于n－1；xi为每次测量值；x为样本平均值；S为测量值标准差；Ua为测量不确定度。

根据公式（3）（4），取置信区间p=95%，按该置信区间下的有效自由度Veff（p）=7，查t分布临界值t0.95（7）=2.36，得S=0.078 1%，Ua=0.069 7%。

2.2 B类不确定度评定

纤维含量的B类不确定度主要为样品质量测量时天平引入的不确定度；进行手拆法实验时，试液的体积、温度等对检测结果没有影响，因此，只考虑天平引入的不确定度。

测量纤维含量所用的电子分析天平符合一级标准，最大误差为±0.05 mg，采用矩形分布；而对于1.0 g样品来说，相对不确定度为0.028 9/1 000=0.000 028 9。

由已做的二组分纤维产品手工分离定量分析不确定度评定方案可以看出，所用天平符合一级标准，不确定度较小。根据微小误差准则，在计算合成不确定度中求“方和根”时，若某一平方值小于另一平方值的1/9，则这一项可以忽略不计。当B类不确定度的值小于A类不确定度的1/3时，可忽略，所以B类不确定度忽略。

2.3 合成标准不确定度评定

合成标准不确定度评定的一般原则是两类不确定度平方加和再开方就得到合成不确定；若数据所涉及的数学模型为积或商的形式，此时要用合成相对标准不确定度来表示。

若B类不确定度忽略的话，可不计算合成不确定度，此时Uc=Ua。

2.4 扩展不确定度评定

在合成标准不确定度后，乘以一个包含因子，取置信区间p=95%，按Veff（P）=7，查t分布临界值t0.95（7）=2.36，则扩展不确定度U=Ua×2.36=0.069 7%×2.36=0.16%。

2.5 测量结果的表述

依据GB/T 2910.1—2009附录B，对同一个棉氨纶混合样品进行手工分解法测量纤维含量，检验结果如下：棉的质量分数为98.50%±0.16%，氨纶的质量分数为1.50%±0.16%。

3 结语

计算结果表明，运用手工分解法实验过程中的重复性对总的不确定度贡献较大，因此，应加强对实验过程中随机性因素的控制，确保取样、拆分、称量等过程符合标准要求，实验重复性不确定度在可接受范围内。