基于二阶SiamRPN多重交并比回归的无人机视觉导航

朱良彬，陈 宇

(中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

0 引言

无人机具有飞行自主、灵活性高、功能扩展性强和造价低廉等优点，在国防、农业、测绘等行业中具有广泛的应用前景[1]。准确的导航以及精准的定位是无人机实现众多功能的基础。目前无人机定位导航技术主要依赖全球导航卫星系统(Global Navigation Satellite System, GNSS)，但是GNSS信号不稳定，容易受到电磁环境与干扰技术的影响，自主性差。因此，探索GNSS失效环境下的无人机自主导航技术，对无人机的安全使用具有重要意义[2-3]。

随着视觉传感器、深度学习的发展，基于景象匹配的无人机视觉导航技术引起了广泛关注。视觉导航技术通过无人机实时采集目标区域的航拍图像，与预存储的基准卫星图像进行匹配，以获取当前的具体位置[4]。视觉导航能同时兼顾准确性和自主性，可以作为独立导航系统，也可以扩展其他导航技术进行联合导航[5]。基于卷积神经网络(Convolutional Neural Network, CNN)的计算机视觉方法已经在目标检测、图像检索等任务中表现出了优异的性能，被作为通用的特征提取器广泛应用于视觉导航定位中。袁浩等[6]使用长短时记忆网络和深度强化学习进行了目标驱动的视觉导航，取得了良好的识别效果和收敛速度。Bertinetto等[7]首次使用全卷积孪生网络(Fully-Convolutional Siamese Network)，通过权值共享的方式将网络分为搜索支和模板支，然后进行特征图的相关操作，匹配出响应最大的区域确定位置信息。孪生网络(Siamese Network)结构简单，可以进行端到端的训练，兼具了匹配精度与速度，因此出现了一系列基于孪生网络的改进算法，例如DSiam，SA-Siam等均取得了良好的效果[8]。Li等[9]在孪生网络的基础上，引入区域建议网络(Region Proposal Network, RPN)构建了SiamRPN，在一个阶段内实现了端到端的目标跟踪，同时提升了网络的匹配精度与速度。但无人机由于高度高、视野大，而目标物体占有的像素少(通常数量级为102)，因此图幅中包含的相似干扰物较多，从背景中区分出目标的难度较大。另外无人机在行进中，实时图像容易产生运动模糊、尺度变化和几何形变等问题，进一步增加了图像中目标识别与定位的困难。

针对以上问题，本文提出了基于二阶SiamRPN多重交并比(Multiple Intersection over Union，MIoU)回归网络的无人机视觉导航算法。通过在孪生框架的CNN提取层引入归一化协方差增加二阶信息，增强特征对边缘的表征能力，提高孪生网络对特征的提取效果。使用区域建议模块对匹配位置进行分类和锚定，并在网络优化过程中提出MIoU损失函数，在一个阶段内实现精确的端到端的特征提取与匹配过程，并在旋翼型无人机搭建平台进行框架验证。

1 相关工作与原理

1.1 深度孪生框架

孪生网络将目标匹配的问题视为相似性学习，由2个分支组成，一个模板支用于提取参考图像T的特征信息，另一个搜索支用于提取当前图像I的特征信息，最终学习到一个相似性度量函数S(T,I)，原理性框架如图1所示。相似性函数返回模板T与输入I对应位置的相似度，并标记相似度最高的部分为匹配目标。经典的SiamFC与其深度改进算法，2个特征提取分支均为权值共享的CNN，通常为AlexNet，ResNet和DenseNet等。然后使用2支特征进行互相关联运算得到相似性得分：

S(T,I)=f(T)⊗f(I)+bl，

(1)

式中，S(T,I)为模板图像T与输入图像I的相似性得分；f(·)表示经过CNN提取到的深度特征；表示相关操作；bl表示当前位置像素的取值。

1.2 区域建议网络

RPN首次在Faster-RCNN网络中提出，在特征图中以锚点(Anchor point)为中心，生成不同尺度的9个锚框(Anchor boxes)并进行前景-背景判断，最终通过边框回归输出目标物体的位置和物体参考分数[10]。多个锚框在深度特征图上以滑动的方式进行枚举，对一个特征图同时进行多个区域的建议，并将结果输入到框回归层与分类层。框回归层通过计算生成框与样本真实框之间的位移获得精确的物体位置坐标，而分类层通过计算锚框和样本真实框之间的交并比(Intersection over Union，IoU)进行前景-背景判断。RPN避免了传统的“选择性”搜索，对不同尺度的目标都有快速且良好的性能和效果。

2 基于二阶SiamRPN多重交并比回归网络的视觉特征点提取

基于视觉的导航技术是将无人机拍摄的实时图像与预存储的卫星图像进行对比，匹配出相似度最高的目标并标记目标的坐标位置。SiamRPN通过在孪生网络后接入RPN模块，能够在一个阶段内完成特征的提取与匹配。但文献[9]中SiamRPN的特征提取主干使用Alexnet，是传统的层数较浅的一阶网络，对图像的特征提取不够充分。而在RPN模块中，使用smooth-l1损失函数约束边框中心、长、宽、高，不具备处理非重叠边框问题的能力，容易产生错位与梯度消失。因此，SiamRPN对大视角内中、小尺度的目标特征提取能力有限。

本文提出基于二阶SiamRPN的MIoU回归算法，通过使用ResNet50[11]替代AlexNet增加网络深度，同时在ResNet50中引入归一化协方差增加特征的二阶信息，充分利用不同分辨率和不同阶特征对目标边缘的提升[12]。算法的优化过程中提出MIoU，增加了对边框尺度和边框中心点之间的约束项目，增强了算法在实时图像非理想状态下的鲁棒性。

2.1 整体框架

图2展示了本文提出的基于二阶SiamRPN MIoU回归网络的框架，由孪生网络和RPN两部分组成。

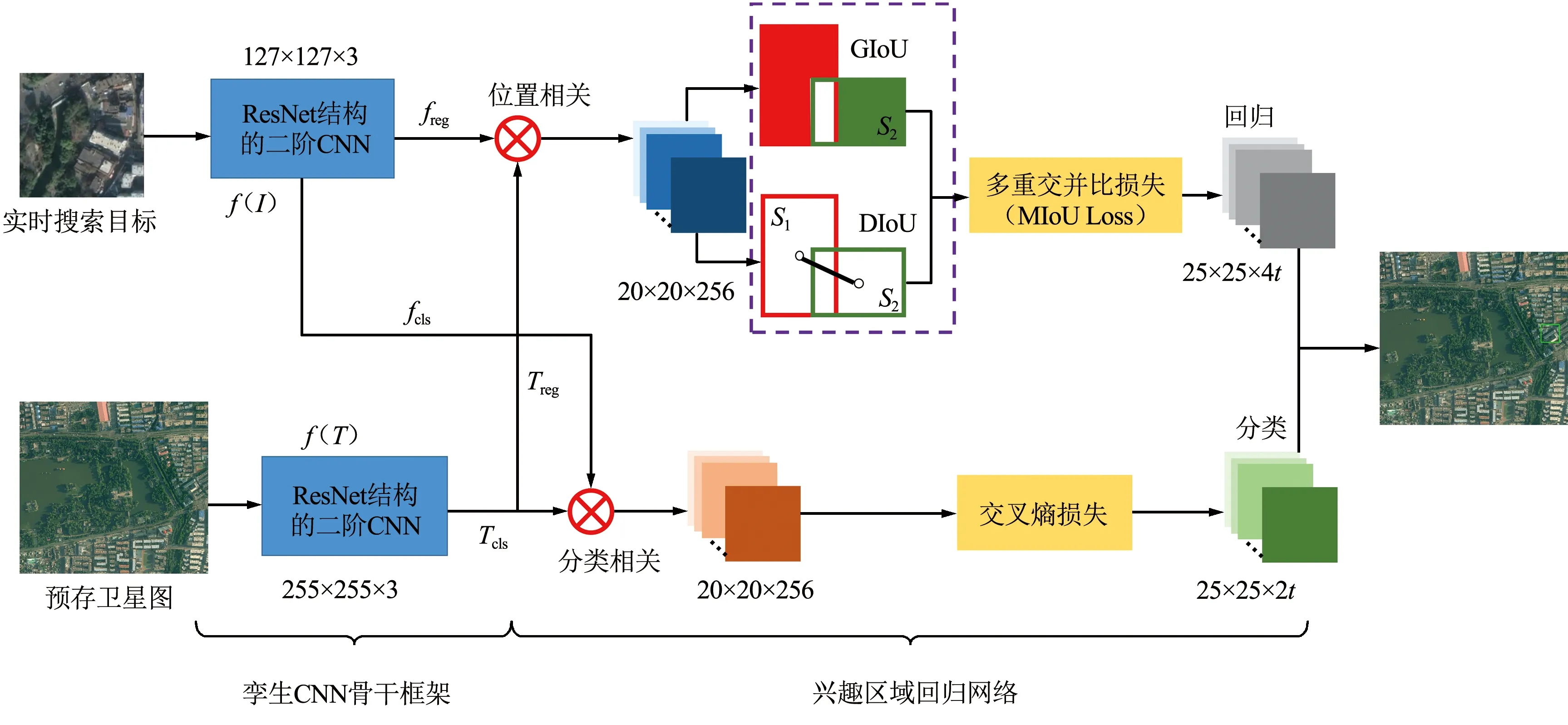
图2 二阶SiamRPN MIoU回归网络框架结构Fig.2 Second-order SiamRPN MIoU regression network framework

孪生网络由2个权值和结构完全相同的ResNet50构成模板支和搜索支，同时在最后一组残差模块嵌入基于归一化协方差的二阶信息，与一阶残差特征相加构成多阶特征信息用于识别与检测。搜索支的输入为255×255×3并包含待匹配的目标物，模板支为127×127×3。2个分支同时对图像的特征进行提取，随后深层特征经过卷积相关后分别进入RPN网络，然后进行相关操作进行类别与位置的预测：

(2)

(3)

式中，Cor表示相关操作后得到的特征，维度分别为w×h×2k和w×h×4k；Tcls和Treg是模板支输入RPN的特征；fcls与freg为搜索支的输入RPN的特征；表示卷积操作。在RPN模块定义了新的MIoU回归边框调节方法，从2个边框非重叠面积与边框中心点2个角度进行联合约束，使预测框与样本真实框靠近。

2.2 基于归一化协方差的二阶特征

将CNN主干网络替换为ResNet网络，一定程度上增加了网络深度，提高了特征的语义表示，但其本质上仍为一阶特征。对于小目标边缘的描述，需要二阶特征的辅助。在残差模块中添加基于归一化协方差的二阶信息，将其设计为嵌入网络的模块化层次，如图3所示。本小节主要介绍归一化协方差的二阶信息的生成方法。

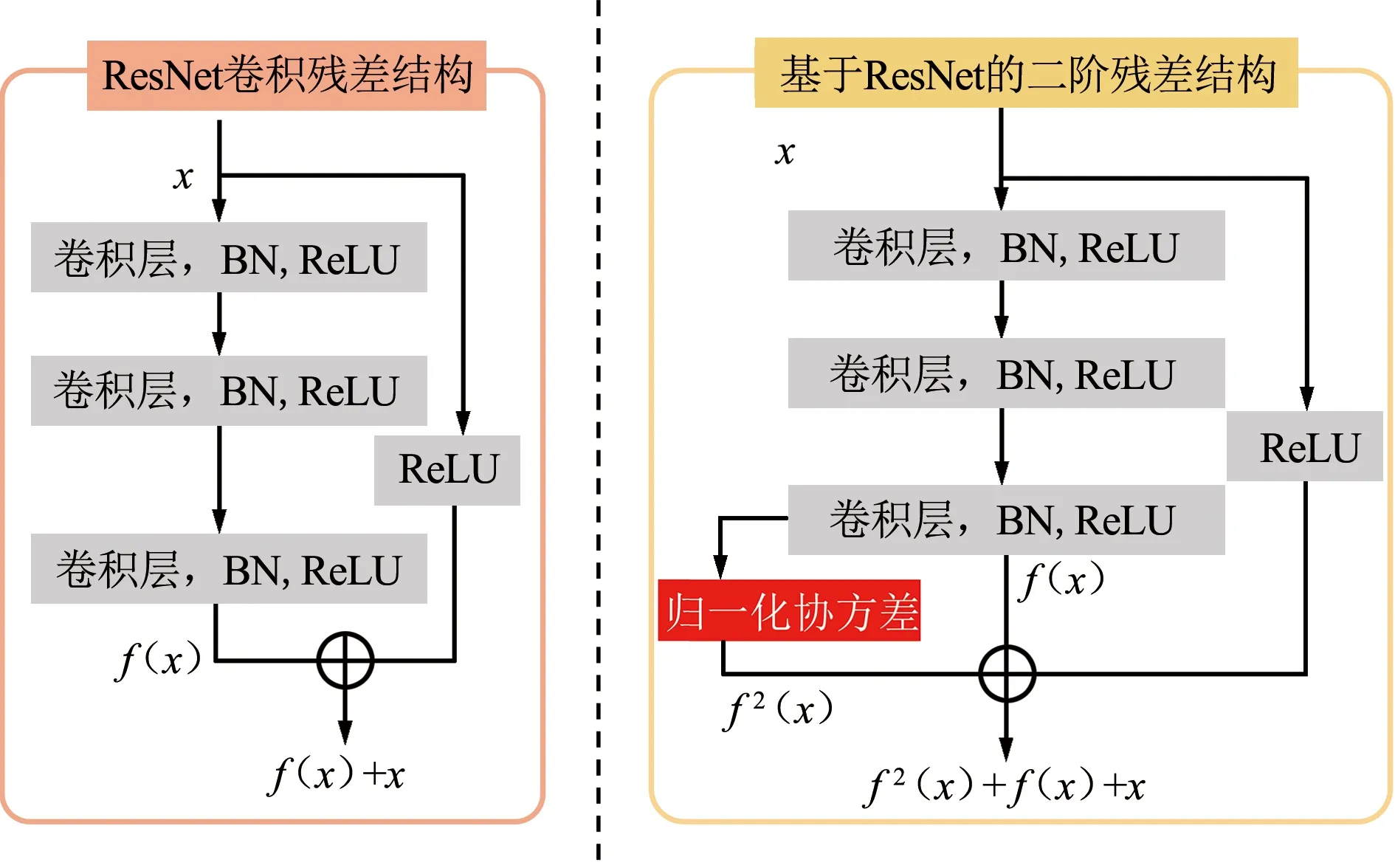
图3 二阶残差信息生成模块Fig.3 Second-order residual information generation module

将图像输入孪生框架后，经过ResNet50提取后获得一组一阶特征fi∈h×w×c，将其转置外积计算后获得了通道间交互的二阶协方差矩阵C：

(4)

式中，fi为提取的一阶特征；I是单位矩阵；ε为一个小正数。但此时得到的协方差矩阵是高维度的小样本，属于黎曼流型结构，模型不能对其进行直接的鲁棒估计。因此对C进行基于特征值分解的归一化处理，如图4所示。

图4 归一化协方差Fig.4 Normalized covariance

因为协方差矩阵C是对称正定的，因此可以进行奇异值分解：

C=UΛUT，

(5)

式中，C为对称正定的二阶矩；Λ=(λ1λ2…λi)是由特征值λi构成的对角矩阵；U=[u1u2…ui]是其对应的特征向量ui组成的n维方阵。由式(5)可知，对于协方差C矩阵幂归一化处理可以表示为特征值的幂运算：

Cα=UΛαUT。

(6)

当α=0.5时，即为矩阵的平方根规范化。由于GPU对矩阵分解的计算速度很慢，为了满足导航实时高的需求，使用迭代计算矩阵的平方根[13]。设有矩阵Z，令C=Z2，则：

F(Z)=Z2-C=0。

(7)

使用Denman-Beavers公式对式(7)迭代求解[14]：

(8)

(9)

式中，给定迭代初始值Y0=C，Z0是单位阵I。则Yk和Zk分别全局收敛于C1/2与C-1/2。

归一化协方差二阶结构作为残差块中的嵌入层，是分段可微的，能够通过反向传播和矩阵计算进行端到端的训练。损失函数L对C的偏导数由链式法则可知，能够表示为：

(10)

式中，L为损失函数；C为二阶特征矩阵；Λ为由特征值构成的对角矩阵；U为由特征向量组成的n维方阵；K为交错矩阵，表示如下：

(11)

式中，kij表示矩阵元素λi对应的特征值，由此可得：

(12)

(13)

(14)

2.3 基于MIoU损失函数的区域建议模块

以SiamRPN结构为框架的算法其损失函数L可以分为2部分，一部分为使用交叉熵损失表示的分类损失Lcls，用于优化目标分类的过程：

Lcls(yi,pi)=-(yi·ln(pi)+(1-yi)·(1-pi))，

(15)

式中，Lcls为损失函数值；yi为样本标签值；pi为该样本对应的概率。由于一个目标仅为一个类别，则式(15)可以简化为：

(16)

(17)

LIoU=-pln(IoU)-(1-p)ln(1-IoU)，

(18)

式中，IoU为交并比比值；LIoU为对应的损失函数；S1为预测锚框；S2为样本真实框；p为其对应的概率。IoU表示2个边框的重叠关系，显然取值为[0,1]。但这种方式没有考虑边框不重叠的情况。使用MIoU对预测框的回归进行多重优化，设计更完整的损失函数，其中包含广义交并比(GIoU)与距离交并比(DIoU)。

GIoU主要关注2框的非重叠部分，其目标是从最小化非重叠面积的角度出发使得2个框无限接近，如图5(b)所示[17]。

图5 不同IoU示意Fig.5 Comparison of different IoU

GIoU首先找到能够完全包裹S1，S2的最小边框，再计算不包括2框占据的区域，即：

(19)

(20)

式中，GIoU为广义交并比比值；S1为预测锚框；S2为样本真实框；S3为完全包裹S1，S2的最小边框。当预测框S1和样本真实框S2没有发生重叠(即IoU=0)，此时GIoU≠0，确保了损失函数的梯度可以反向传播。但当S1包含S2时，GIoU退化为IoU，无法进行准确的回归计算。因此引入DIoU，可视化如图5(c)所示[18]。DIoU在回归中加入对S1，S2中心距离的约束，更好地表征重叠信息，计算过程如下：

(21)

(22)

式中，DIoU为距离交并比比值；IoU为交并比值；d(S1,S2)为2个框中心点的距离；R为包含2个框的最小矩形的对角线。不同IoU之间的示意如图2紫色框中所示。因此基于MIoU的回归损失函数Lreg为GIoU的DIoU的组合：

(23)

式中，Lreg为回归分支的损失函数；α与β为超参数。则整体框架的损失函数Loss可以表示为:

Loss=Lcls+Lreg，

(24)

即：

(25)

3 实验结果及分析

3.1 实验设置与实验环境

本实验选用旋翼型无人机为实验载机，数据集为无人机采集的3 960张地形匹配图，经过平移、缩放、模糊和翻转等数据增强处理扩充为10 000张，地形涵盖山地、森林、河流、湖泊、海岸线、城市十字路口、操场、工厂楼房、独栋楼房、小区楼房、高架桥、公园、不带绿化带的马路以及带绿化带的马路等类别。

本文使用PyTorch框架搭建网络，训练的epoch为50，batch size为128，采用随机梯度下降算法进行网络优化，设置动量因子为0.9，权重衰减为0.000 1，前5个epoch使用Warmup预热学习率从0.005增加到0.01，之后学习率以指数衰减方式从0.01到0.005。前10个epoch不训练backbone只训练模型剩余部分，10个epoch后训练整个模型。超参数α与β经多次实验后分别为0.41与0.53。实验使用的CPU为Intel-Core i7-8700K@3.70 GHz，GPU为NVIDA RTX3090显卡，显存为24 GB。

为验证二阶SiamRPN MIoU回归框架的有效性，使用精确度(Precision)、成功率(Success)和运行速度(FPS)对算法进行定量评价。Precision的像素阈值选择20，Success采用重叠率作为标准。同时，使用目前匹配定位效果优异的算法SiamFC[7]，SiamRPN[9]，CFNet[19]进行了对比。

3.2 实验结果

本文提出的二阶SiamRPN MIoU回归算法与其他基准算法的Precision和Success曲线如图6和图7所示，均使用曲线下面积作为标准。结果表明，二阶SiamRPN MIoU回归比结构相同的基准SiamRPN的精确度与成功率分别提升了0.023和0.022，运行速度基本持平，远高于其他结构的算法框架，如表1所示。

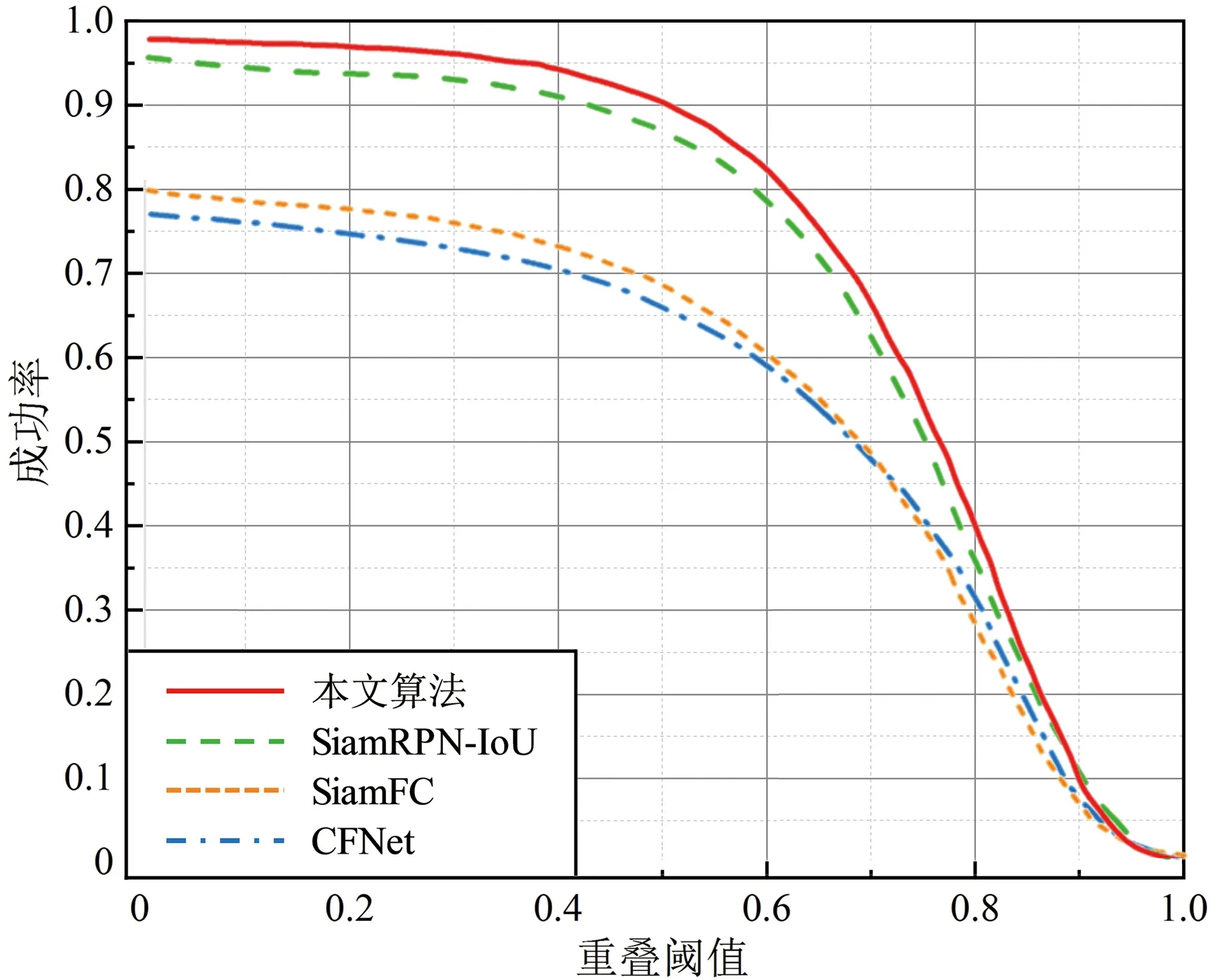
图6 成功率曲线Fig.6 Success curve chart

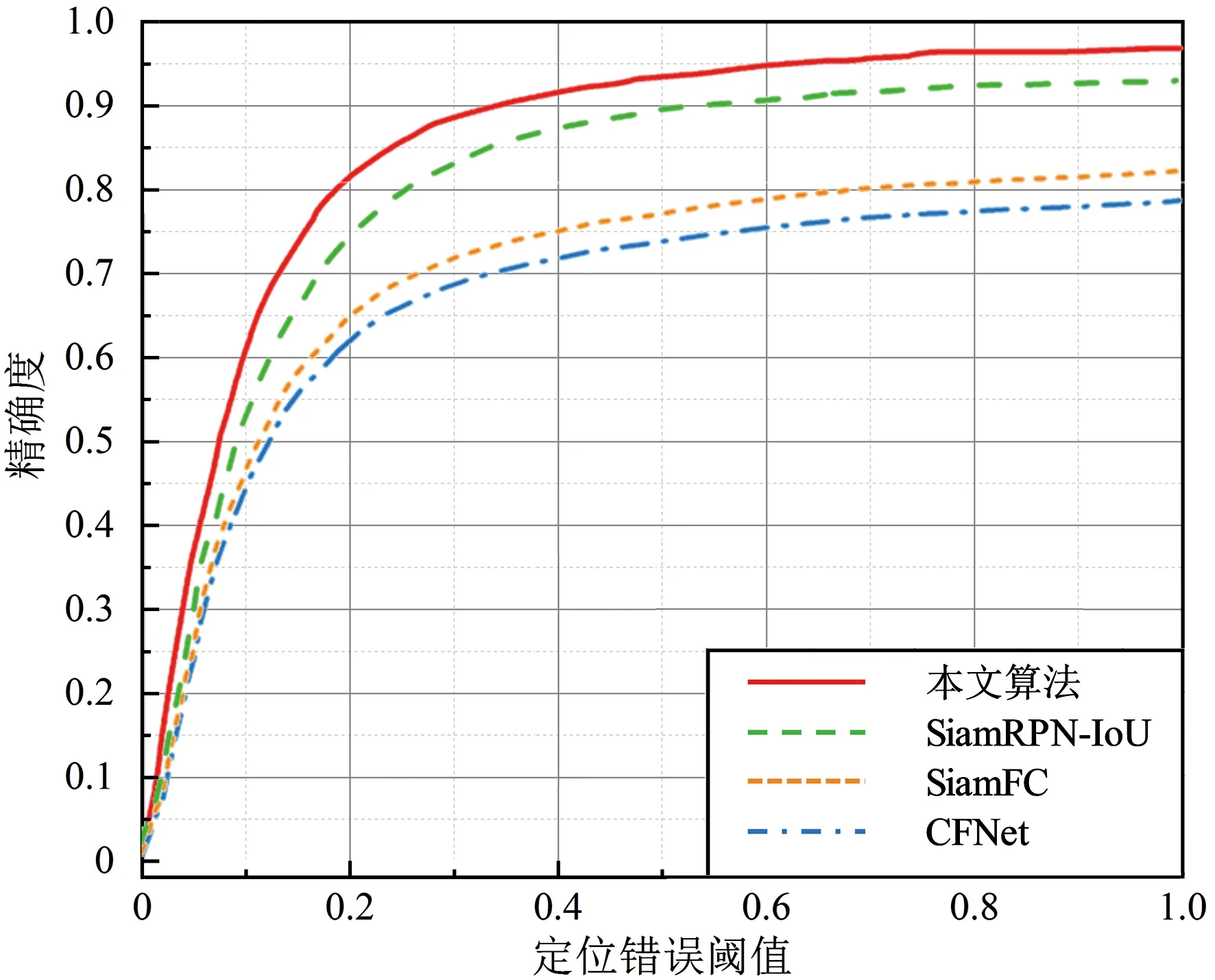
图7 精确度曲线Fig.7 Precision curve chart

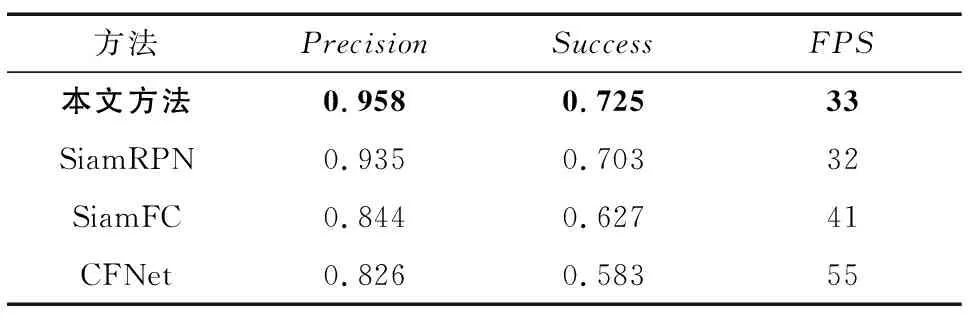
表1 二阶SiamRPN MIoU回归算法性能比较Tab.1 Performance comparison of second-order SiamRPN MIoU regression network with other methods

为了验证所提MIoU的有效性，使用二阶SiamRPN框架与多种Loss函数的组合，分别为二阶SiamRPN+smooth-l1，二阶SiamRPN+IoU，二阶SiamRPN+GIoU，二阶SiamRPN+DIoU以及二阶SiamRPN+MIoU。其在自建数据集上的中心误差值比较如表2所示，本文所提方法显著好于其他组合。

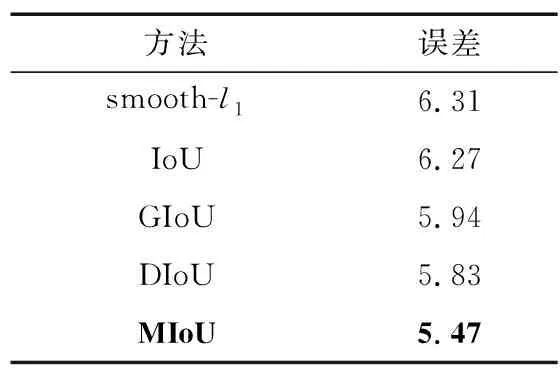
表2 MIoU与其他损失函数平均中心误差对比Tab. 2 Comparison of the mean central error of MIoU and other loss functions

图8展示了本文所提二阶SiamRPN MIoU回归算法和SiamRPN算法对部分样本的定位结果。其中，第1列为无人机实时航拍采集的图像，第2列为本文所提算法匹配结果，第3列为SiamRPN算法匹配结果。

(a)本文所提方法与基准SiamRPN均定位正确样本

(b)本文方法定位正确，但基准SiamRPN定位错误样本图8 无人机实时定位结果Fig.8 Real-time location results of the UAV

图8(a)展示了正确匹配并定位的结果，可以看出当图像中出现比较明显的特征(例如鲜艳的颜色、特殊的边缘)，2种方法都有优异的效果。但当检索图像中目标比较模糊或与周围有相似轮廓时，传统的SiamRPN比较容易发生错误定位，而二阶SiamRPN MIoU回归方法依然能正确定位，如图8(b)所示。算法性能的提升主要在于二阶协方差信息的融合，使骨干CNN对目标物体特征的提取更加充分，对模糊边缘的可分性增强。另外，由于MIoU损失函数纳入了多重回归因素，锚框的定位更加准确。

4 结束语

目前，基于深度学习的视觉导航在GNSS拒止条件下给无人机提供导航定位。但无人机由于高度高、视野大，在行进中有抖动，实时图像中存在目标物体像素少、运动模糊、尺度变化、几何形变和部分遮挡等问题，需要特征提取与定位能力强的算法框架。为此本文提出了基于二阶SiamRPN MIoU回归算法，包括双流孪生特征提取模块、二阶协方差信息生成模块、多重约束的兴趣区域产生模块。通过Res50主干网络对模板图像和搜索图像的特征进行提取，同时生成二阶协方差信息对特征进行描述，提升网络对模糊边缘的表征能力；将孪生框架的信息进行交互操作，分别进入分类与定位分支；设计基于GIoU和DIoU双重约束的MIoU损失函数对RPN的定位回归进行优化，同时提高了定位精度和成功率。最后搭载旋翼型无人机，自制数据集进行验证测试，分别与当前先进的多种算法进行了对比，验证了本文所提算法的有效性。未来的工作将进一步研究提升基于深度学习的视觉导航实时性与轻量化，推动机载导航硬件部署的一体化。