多跨连续梁-刚构桥地震易损性分析

2023-03-07张卓航班亚云

郑州大学学报（工学版） 2023年1期

梁岩, 张卓航，班亚云，王艳

(郑州大学土木工程学院，河南郑州 450001)

公路桥梁是交通工程的重要组成部分，近年来国内外桥梁抗震性能评价、加固改造实践和震害经验表明，对公路桥梁进行抗震性能评价，并对不满足评价要求的桥梁采取适当的抗震加固改造对策，是减轻地震灾害的重要途径[1]。桥梁地震易损性分析是桥梁抗震性能评价的重要依据[2]，可预测在地震作用下，结构达到或超越某一损伤指标的概率。易损性分析方法在考虑地震动随机性及结构损伤不确定性的同时，能够有效地将桥梁在地震中的失效概率和桥梁的承载能力建立起某种概率上的联系。户东阳[3]基于往年收集的渝昆高铁沿线实测地震动记录资料，研究了不同形式支座的抗震性能，以及桥墩的地震易损性。王君[4]、陈伟等[5]均以国内典型的高速铁路桥梁为工程背景，采用地震时程分析方法(IDA)对桥梁的地震易损性进行分析。Basoez等[6]同样根据收集的震害资料，依据逻辑回归法，分析地震作用下桥梁构件的易损性。

随着国内高烈度区公路桥梁的建造，多跨连续梁-刚构桥逐渐增多，研究该桥型地震易损性对其抗震性能评估有重要意义。而国内外对桥梁地震易损性的研究多集中于桥墩，对于耐久性损伤下桥墩抗震性能的研究仅针对带支座的桥墩，未考虑墩顶约束作用，未重视服役期内材料性能的退化，且忽略了桥梁系统的损伤概率与单一构件的损伤概率之间的差异性，仅以构件的损伤概率分析地震作用下桥梁整体的损伤，导致结构存在安全隐患。

本文基于地震易损性分析理论对某多跨连续梁-刚构桥梁构件(桥墩、支座、桥台)进行易损性研究，分析桥梁构件在地震作用下的失效概率，并采用界限法评估整个桥梁系统的抗震性能。

1 非线性有限元模型建立

OpenSEES可对结构进行模态分析、动力非线性分析以及结构体系在地震作用下的可靠性分析[7]。基于OpenSEES建立某连续梁-刚构桥非线性有限元模型。该桥长6×60 m，桥型如图1所示。

图1 算例桥梁计算简图 (m)Figure 1 Diagram of the example bridge (m)

主梁等高(3.35 m)，采用C50混凝土。桥面宽度为12.2 m。桥墩1#、4#及5#为分离式菱形实体墩，采用C40混凝土；2#、3#墩采用C50混凝土，为墩梁固接桥墩。纵筋为32 mm带肋钢筋，屈服强度335 MPa；箍筋为16 mm光圆钢筋，屈服强度235 MPa。该桥实际工程所处位置墩底主要为弱风化岩，Ⅱ类场地。所处区域7度抗震设防，地震分组为第一组。各构件在不同损伤状态下用以评估的损伤指标Sc和不确定性βc见表1。

表1 桥梁不同构件的损伤指标及不确定性Table 1 Damage index and uncertainty of different bridge components

采用OpenSEES材料库中的Concrete 01本构和Steel 02本构分别对混凝土材料和钢筋材料进行模拟。桥墩非线性特征采用Nonlinear Beam Column模拟，桥梁上部结构采用Elastic Beam Column模拟，桥台球型支座采用非线性连接单元模拟及ZeroLength Element模拟。依据本课题组前期所做钢筋混凝土柱试验[8]建立模型，采用相同加载方式加载，对比模型模拟结果与实际试验结果如图2所示。试验结果与计算结果较为吻合，验证了建模方法及建模参数的可靠性。

图2 滞回曲线对比Figure 2 Hysteretic curve comparison

根据算例桥梁所处区域的地质条件，基于抗震设计规范[9]生成目标反应谱。依照所生成的反应谱，从PEER强震库中合理选取地震强度等级均为7级的地震动记录，用作非线性动力分析的原始地震动。所生成的目标反应谱以及整合后的均值反应谱如图3所示。

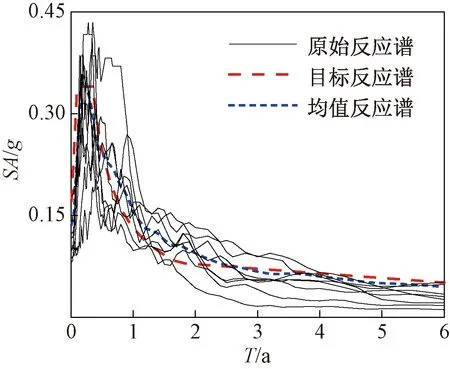
图3 地震动反应谱 (ξ=0.05)Figure 3 Seismic response spectrum (ξ=0.05)

地震反应谱加速度SA对地震动拟合效果较好[10]。选取SA作为地震动强度指标，以桥梁第一阶周期1.012 s所对应的实测SA为基准调整，使其均匀分布于0.1g～1.0g，形成10组共150条不同等级的地震数据，对有限元模型进行非线性动力时程分析。IDA分析中地震动的调幅公式：

ag(i)(t)=kia(t)。

(1)

式中：ag(i)(t)为第i次调幅后地震动；a(t)为原始地震动；ki为调幅系数。

2 关键构件易损性分析

分析桥梁各构件在模拟地震动下的易损性，得到在不同强度等级的地震作用下桥台、支座、桥墩达到各损伤指标状态的超越概率。

根据易损性分析理论，对模型输入所选取的150条地震动并进行非线性动力分析，采用IDA分析方法，调幅地震动，得出计算样本数据点，用对数线性回归分析方法整合数据点，得出各构件在地震作用下需求响应值与反应谱SA的对数拟合函数。结合表1给出各构件的损伤指标参数，根据式(2)计算构件失效概率[11]：

(2)

式中：Pf为失效概率；IM为地震动强度参数；βd为结构在地震作用下最大反应的对数标准差，参见式(3)取值[12]：

(3)

分别计算各构件(桥墩、支座、桥台)在不同强度地震作用下，所产生轻微损伤、中等损伤、严重损伤以及完全破坏下的超越概率并绘制曲线，对比分析其易损性曲线，评估桥梁各构件的抗震性能。

2.1 桥墩易损性分析

取各桥墩的150个不同强度地震(0.1g～1.0g)作用下的响应值和对应的地震动反应谱加速度SA，采用对数线性回归方法，得到各桥墩的地震响应值与SA的对数回归分析结果，将结果代入式(2)，从而得到各桥墩的易损性函数式。

为计算桥墩的地震易损性损伤指标，通过弯矩-曲率分析，计算桥墩钢筋屈服时曲率值并计算其等效屈服曲率φ′y及混凝土应变εc=0.004 时的曲率φc4，将曲率值代入并得到桥墩不同损伤状态时的损伤指标界限值μcy1、μcy、μc4、μcmax：

(4)

(5)

(6)

(7)

μcmax=μc4+3。

(8)

式中：Δcy为桥墩屈服时墩顶相对位移；Δc4为混凝土截面最外侧应变εc达到0.004时墩顶相对位移；Lp为等效塑性铰长度；L为悬臂桥墩墩高。

所得桥墩损伤状态指标如表2所示。1#、3#和5#桥墩易损性曲线如图4所示。

表2 桥墩损伤状态指标Table 2 Damage status index of pier

图4 桥墩地震易损性曲线Figure 4 Seismic fragility curve of the pier

在不同损伤状态下，各桥墩的超越概率随SA的增大明显升高；对比各桥墩发生在轻微损伤、中等损伤、严重损伤、完全破坏的易损性曲线，前3种较为接近，且随着地震强度增大其超越概率在0.2～0.7之间上升较快，0.7之后趋于平稳；同一地震强度下，桥墩出现完全破坏的概率明显低于其他损伤的概率。

为分析桥墩类型对自身易损性的影响，各桥墩不同损伤状态下的超越概率曲线见图5。

图5 桥墩在不同损伤状态下的地震易损性曲线Figure 5 Seismic fragility curves of the pier in different damage states

对于1#与4#桥墩，谱加速度SA=0.6g时，轻微损伤、中等损伤以及严重损伤状态的超越概率大于80%，完全破坏概率较小，约为20%；5#桥墩在谱加速度SA=0.6g发生轻微损伤、中等损伤、严重损伤以及完全破坏的概率分别为60%、45%、34%、1%；2#和3#桥墩在谱加速度SA=0.6g出现轻微损伤、中等损伤、严重损伤概率小于9%，完全破坏概率较小。

由于桥墩延性变形能力与桥墩高度呈现正相关，且1#、4#及5#桥墩混凝土采用C40，比2#与3#桥墩C50强度低，同时由于上部梁体对刚构墩的固结作用，在相同损伤状态下，1#与4#桥墩出现损伤概率较大，5#桥墩次之，2#和3#桥墩的概率最小，随着墩高增加，桥梁变形能力增大，其地震易损性逐渐减小。

由于1#和4#墩高度接近且均为支座墩，易损性曲线基本相同；2#和3#墩高度接近且均为墩梁固结，易损性曲线基本相同。桥墩易损性与材料强度、墩高、墩梁连接方式及墩顶荷载等有关。

2.2 支座、桥台易损性分析

易损性分析方法与桥墩相同。支座位移损伤指标和桥台位移损伤指标如表3所示。支座易损性曲线未单独绘制，将与其他构件共同分析。左、右桥台易损性曲线见图6。

表3 支座和桥台损伤状态指标Table 3 Damage status index of support and abutment

图6 桥台地震易损性曲线Figure 6 Seismic fragility curves of the abutment

桥台不同损伤状态下的易损性曲线斜率较大，在SA=0.4g时，发生轻微和中等损伤状态的概率均高于90%，在SA=0.6g时，严重损伤和完全破坏的超越概率分别为69%、30%；左右桥台发生同一损伤的易损性曲线无明显差别。

3 耐久性损伤桥墩时变地震易损性分析

本文基于桥址位置并参考《混凝土结构耐久性评定标准》(CECS 220—2007)[13]，以5#桥墩为例，分析近海环境下其氯离子侵蚀致使钢筋锈蚀的变化规律，得到不同服役期钢筋各项参数值，见表4。

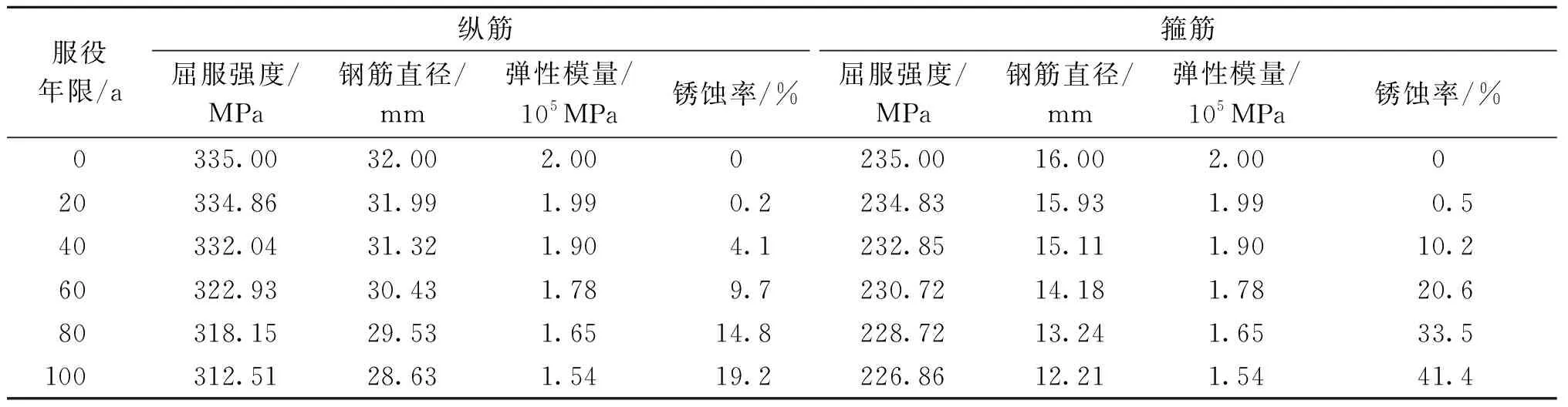
表4 不同服役期的钢筋特征值Table 4 Characteristic values of reinforcement in different service periods

为研究不同服役期钢筋的锈蚀率对桥墩地震响应的影响，首先计算桥墩在0、20、40、60、80、100 a服役期力学性能，基于已建立的OpenSEES非线性有限元模型，对比分析不同服役期内易损性曲线如图7所示。

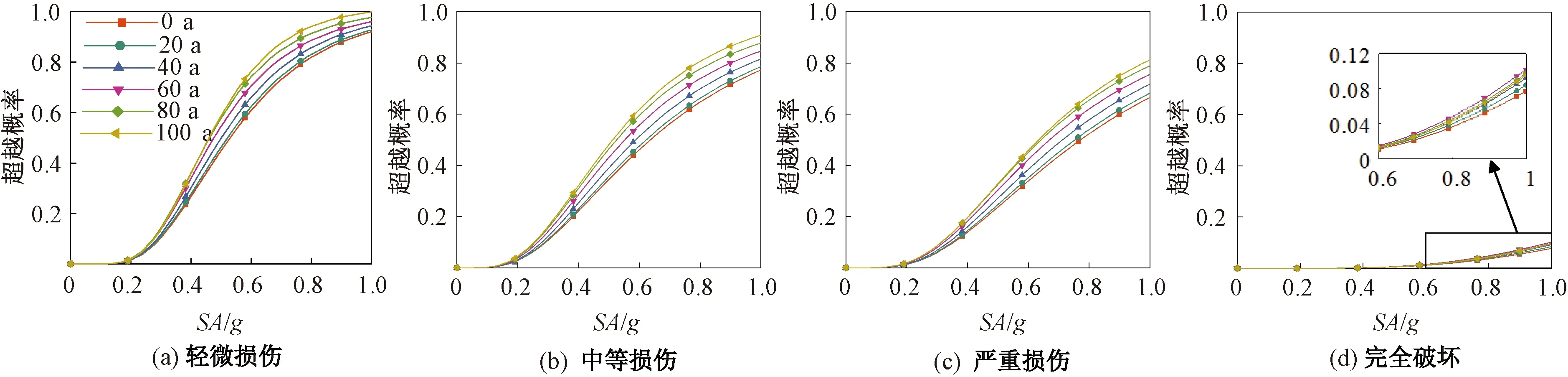
图7 桥墩时变易损性曲线Figure 7 Time varing fragility curve of pier

结果显示，在同强度地震作用下，5#桥墩在4种状态的易损性随着服役期增加而逐渐升高。相比于0 a钢筋未锈蚀的桥墩构件，20、40、60、80、100 a服役期的超越概率在中等损伤状态下，分别增大3.1%、11.3%、20.9%、29.1%、34.1%；严重损伤状态下，分别增大3.9%、13.5%、25.1%、33.4%、35.4%。

4 桥梁系统易损性分析

桥梁结构理论中串联体系和并联系统的失效概率[14]可用以下公式计算：

Psys=P(F1∪F2∪F3∪…∪Fn)

(9)

图8 桥梁系统在不同损伤状态下的地震易损性曲线Figure 8 Seismic fragility curves of the bridge system in different damage states

(10)

式中：Psys为整个系统失效的概率；Fi(i=1,2,…,n)表示结构第i个构件失效。

根据各个构件的易损性函数从而建立整个工程结构系统的易损性函数，即界限估计法。一阶界限法通过假定桥梁构件失效模式的正相关性 (ρ=0和ρ=1)，评估桥梁系统的最大与最小失效概率，从而确定系统失效概率的上限值和下限值，可表示为[15]

(11)

式中：Pi为第i个构件发生破坏的概率；m为构件数目。

一阶界限法上限值的计算公式为

(12)

根据桥墩、支座和桥台的地震易损性分析结果，桥梁系统在各损伤状态下的易损性曲线界限值如图8所示，汇总桥梁各构件以及桥梁系统易损性曲线于图9。

图9 桥梁系统与各构件在不同损伤状态下的地震易损性曲线Figure 9 Seismic fragility curves of the bridge system and each component in different damage states

由于桥梁各构件的最大超越概率决定了系统易损性的下限值，相比于单个构件，桥梁系统超越概率更大，SA=0.6g时发生严重损伤的超越概率已经达到95%以上。若忽略各主要构件对全桥系统抗震性能的影响，以单个构件的易损性来评估桥梁系统的易损性，会高估桥梁抗震性能。

桥梁不同构件的易损性存在较大差异。对于本文实际工程，2#和3#支座最易发生轻微破坏，其次是桥台，2#和3#刚构墩发生轻微破坏的概率最小；中等损伤状态下，两个桥台易损性最大，其次为1#和4#桥墩，对于2#和3#桥墩以及4#支座最不易发生中等损伤；1#和4#桥墩最易发生严重损伤，其次是两个桥台，SA=0.6g时桥台发生严重损伤的超越概率为60%，2#、3#桥墩以及4#支座严重损伤概率较小，SA=0.6g时，1#、5#支座较2#、4#支座发生严重损伤的超越概率增大25%；两个桥台和5#支座完全破坏的概率较大，2#和3#桥墩发生完全破坏的概率较小。整体而言，该桥梁两个桥台相对薄弱，2#、3#桥墩以及4#支座在相同损伤状态下的超越概率低于其他构件。