推进轴系纵向高承载准零刚度隔振器的研究

任志英， 邱 涛， 刘扭扭， 白鸿柏， 尧杰程， 梁 翼

(1.福州大学金属橡胶与振动噪声研究所,福建 福州 350116; 2.福州大学 机械工程及自动化学院, 福州 350116)

船舶运行过程中，推进轴系产生的纵向振动会严重影响船舶可靠性与静谧性[1]。相较于主动隔振，被动隔振方案可靠性更高、结构简单，更适用于推进轴系的纵向隔振。Goodwin[2]在上世纪60年代首先利用共振转换器来减小推进轴系的纵向振动，并取得了良好的效果。随后国内外相关学者对共振转换器的轴向隔振性能进行了更深入的研究[3-7]，在推进轴系纵向振动的控制中取得了较好的成果，但是难以满足实际中越来越严格的低频隔振要求。

1 准零刚度隔振器布置方案

图1为碟簧-螺旋弹簧并联实现的准零刚度隔振器。当碟簧的压缩量达到Δf时，碟簧在该平衡点附近产生的负刚度正好抵消螺旋弹簧的正刚度，机构的总刚度为零，此时可以有效隔离低频振动。

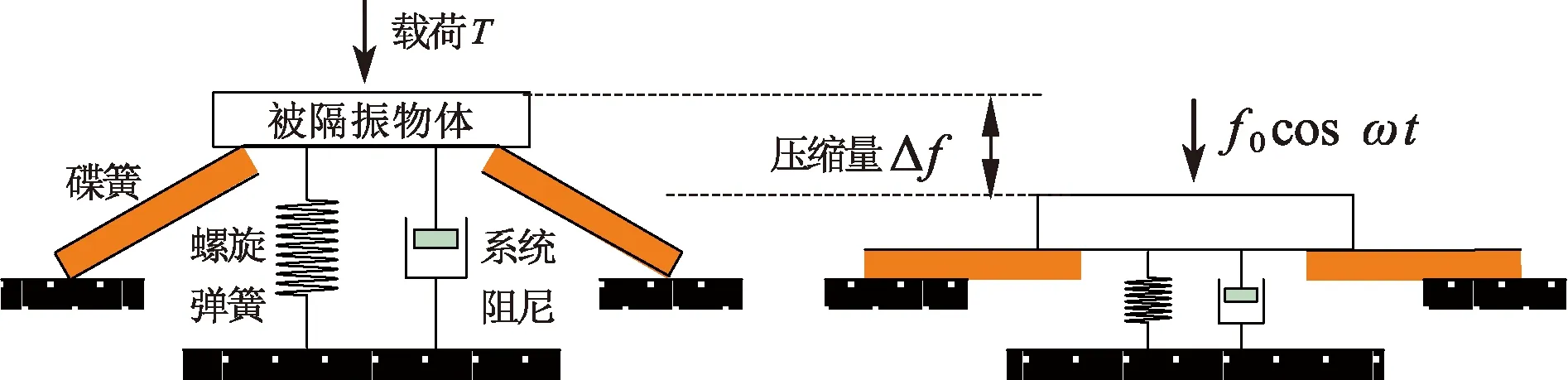
图1 碟簧-螺旋弹簧并联示意图Figure 1 Schematic diagram of parallel connection of disc spring and coil spring

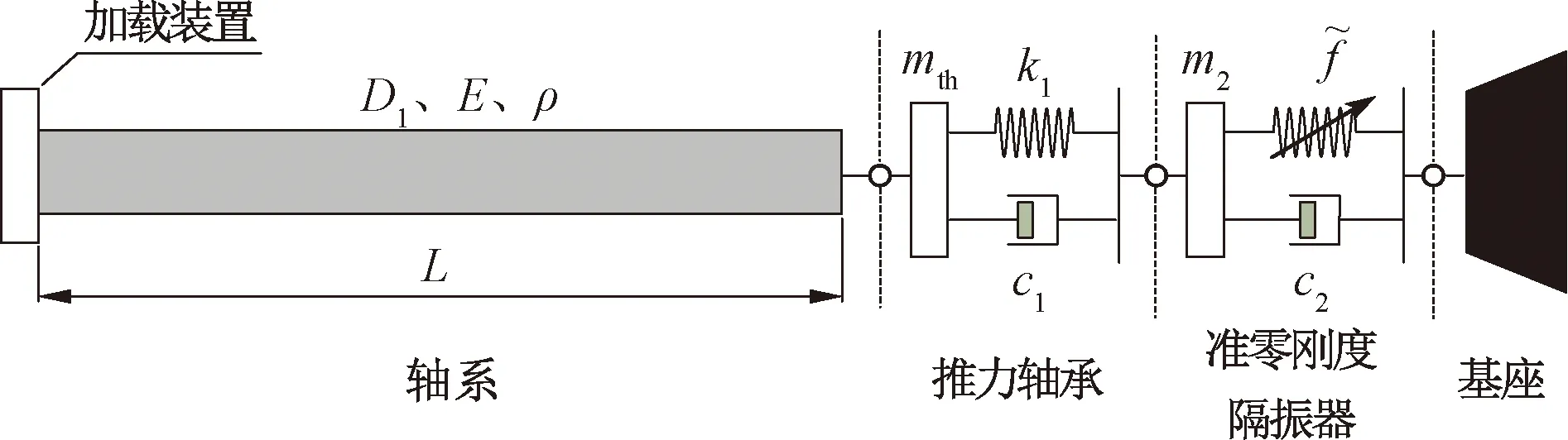
图2 推进轴系纵向低频隔振示意图Figure 2 Schematic diagram of longitudinal low frequency vibration isolation of propulsion shafting

2 轴系纵向动力学分析

2.1 动力学方程建立与求解

根据图2建立了轴系-准零刚度隔振器的动力学模型，如图3所示。在研究低频范围内轴系纵向振动时可以将其简化为单自由度，用质量m1表示；在平衡位置处，准零刚度隔振器的回复力与位移可以近似为三次方关系，并用kqzs表示非线性刚度；由于基座刚性大，因此可以将基座视为固定端；其他符号意义与第1节相同。

图3 轴系-准零刚度隔振器动力学模型Figure 3 Shafting-quasi-zero stiffness isolator dynamic model

图3的动力学方程可写成：

(1)

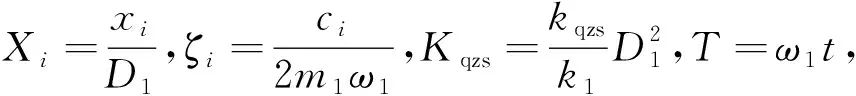
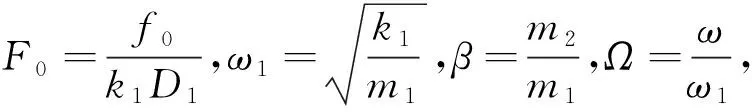
(2)

设该系统的稳态响应解为

(3)

将式(3)代入式(2)中，采用谐波平衡法进行求解，仅保留一次谐波项，并令各谐波项系数相等可得

(4)

解析解可通过求解式(4)获得。

2.2 求解有效性的验证

本文中轴系结构参数L=3 m，D1=0.08 m，E=206 000 MPa，ρ=7 800 kg/m3，并取kqzs=1×1013N/m3、f0=75 N、ζ1=0.02、ζ2=0.02、β=0.1来验证解析法求解的有效性。用四阶龙格-库塔法求解方程(2)，x2的幅值用A2表示。解析解与数值解的结果对比如图4所示，可以看出数值解与解析解的吻合度高，说明用谐波平衡法进行求解是可行的。

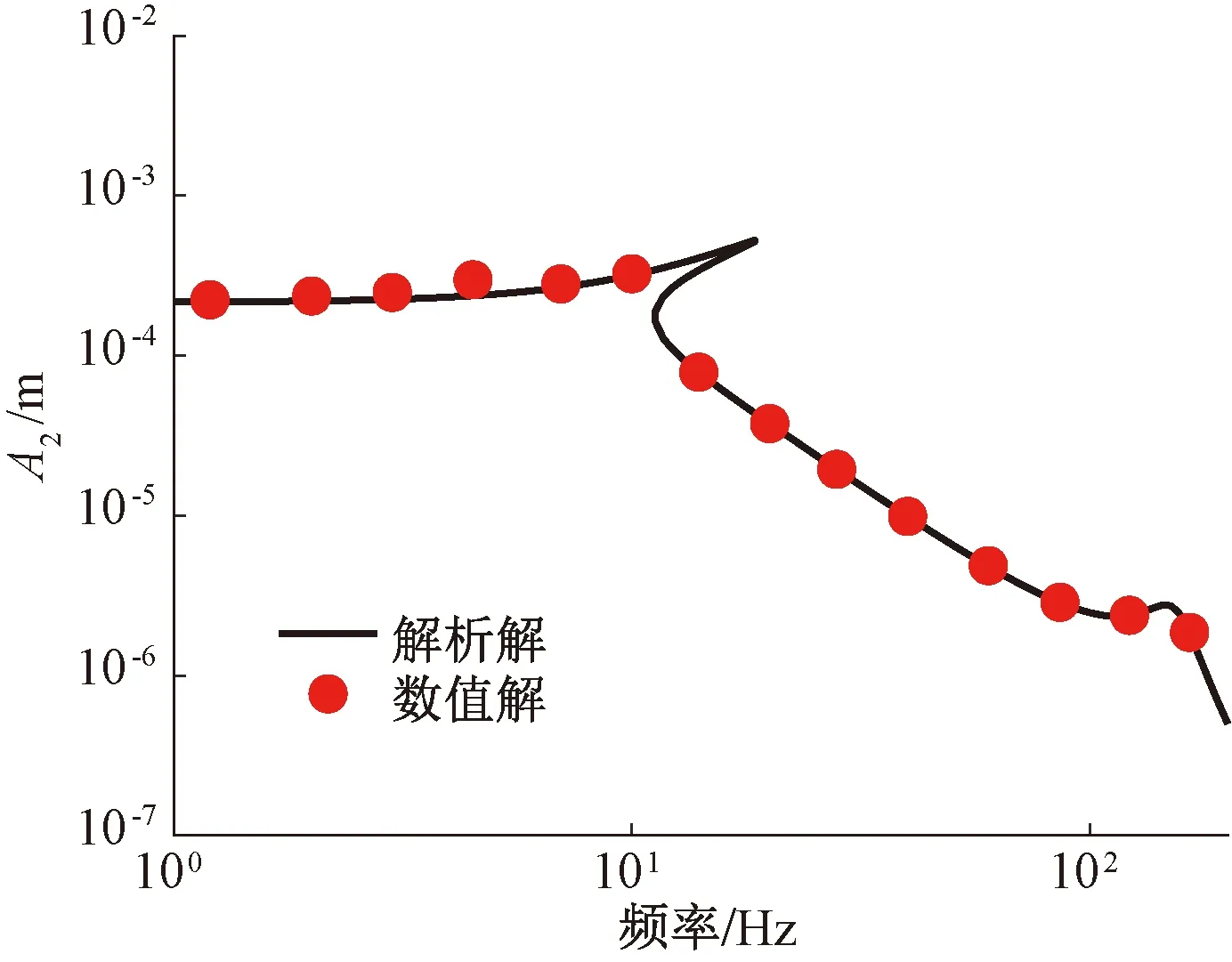
图4 解析解与数值解对比Figure 4 Analytical solutions compared with numerical solutions

2.3 系统力传递率曲线

用力传递率来评价准零刚度隔振器的隔振性能。力传递率定义为Tf=ft/f0，其中ft为传递到基座上的力，f0为激励力幅值，并将传递率转换为分贝的形式，即20lgTf,无隔振器系统与加入隔振器系统的力传递率曲线如图5所示，无隔振器系统的起始隔振频率为65.7 Hz；加入隔振器的系统的起始隔振频率为18.5 Hz，且在18.5～200 Hz频段内力传递率相较于无隔振器系统大幅降低。

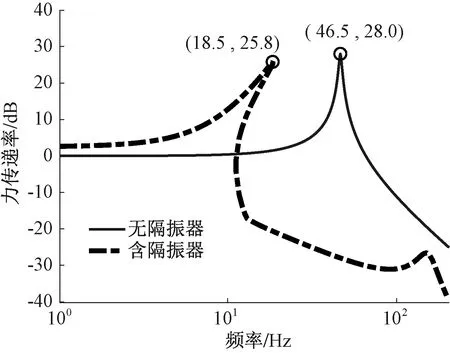
图5 力传递率曲线Figure 5 Force transmission rate curve

3 准零刚度隔振器参数对系统稳定性的影响

准零刚度隔振器具备优秀的低频隔振性能，但在实际运用中，其非线性特点可能会影响实际的隔振效果，因此，分析系统的稳定性是十分有必要的。对式(2)求得的稳态解施加一个小扰动，方程的解可以写成：

(5)

式中:Xi表示方程(2)的稳态解，i=1，2。

将式(5)代入式(2)中并忽略高阶的非线性项，得到如下关于小扰动ui的线性化方程：

(6)

设方程(6)的解为如下形式：

(7)

将式(7)代入方程(6)中并保留一次谐波项，令其各谐波项的系数等于0可得如下方程：

(8)

将式(8)写成矩阵形式A[a1b1a2b2]T=0，若矩阵A的行列式Δ<0，则系统的响应是不稳定的。

3.1 非线性刚度对系统稳定性的影响

讨论不同非线性刚度对系统响应稳定性的影响时，取阻尼比ζ2=0.03进行分析。图6(a)、6(b)、6(c)分别表示不同非线性刚度下，系统的幅频响应与不稳定区间，其中虚线为系统的不稳定边界，边界内部为系统的不稳定区间。图6(d)表示激励力幅值为75 N时，系统的幅频响应随非线性刚度变化的曲线。

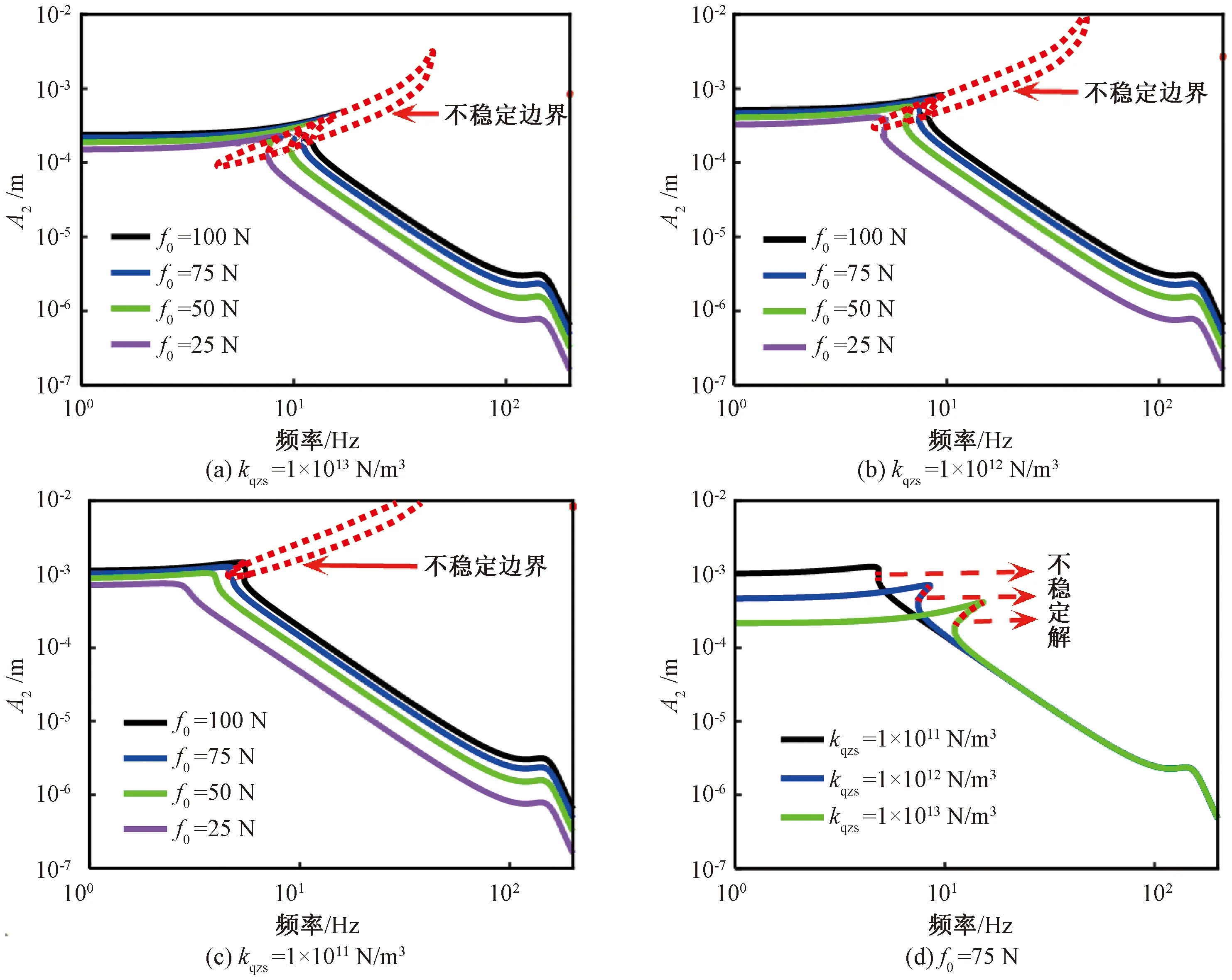
图6 不同非线性刚度幅频响应与稳定性图Figure 6 Amplitude-frequency response and stability diagram of different nonlinear stiffness

由图6可知，当非线性刚度一定时，激励力幅值越小，系统幅值的响应越小，且起始隔振频率也越低。此外系统不稳定解的区间也会随着激励力幅值的减小而减小。激励力幅值一定时，系统的非线性刚度越大，对应的起始隔振频率也越高，不稳定的跳跃现象越明显，较小的非线性刚度能避免系统的响应出现过大的不稳定区间。但在实际中考虑到艉轴承密封的要求，推进轴系的轴向静变形有一定限制[17]，这表明非线性刚度不宜选取过小。综上所述，选取非线性刚度为1×1012N/m3。

3.2 碟簧与螺旋弹簧的设计

确定非线性刚度后，可根据相关静力学理论设计碟簧与螺旋弹簧结构参数。碟形弹簧示意图如图7所示。

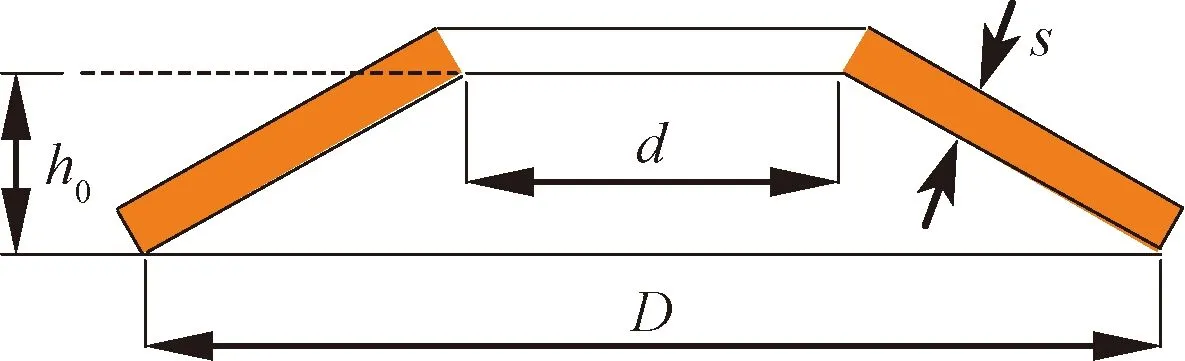
图7 碟形弹簧示意图Figure 7 Schematic diagram of disc spring

常用碟簧的载荷-位移曲线可以根据A-L解[18]近似求出：

(9)

式中：E为弹性模量，MPa；μ为泊松比；f为碟簧的压缩量，mm；D、d分别为碟簧外径与内径，mm；s为碟簧厚度，mm；h0为自由高度，mm；M的表达式见式(10)，其中C为外径与内径之比。

(10)

式(9)对位移f求导，得刚度-位移表达式：

(11)

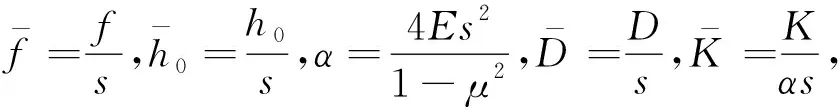
(12)

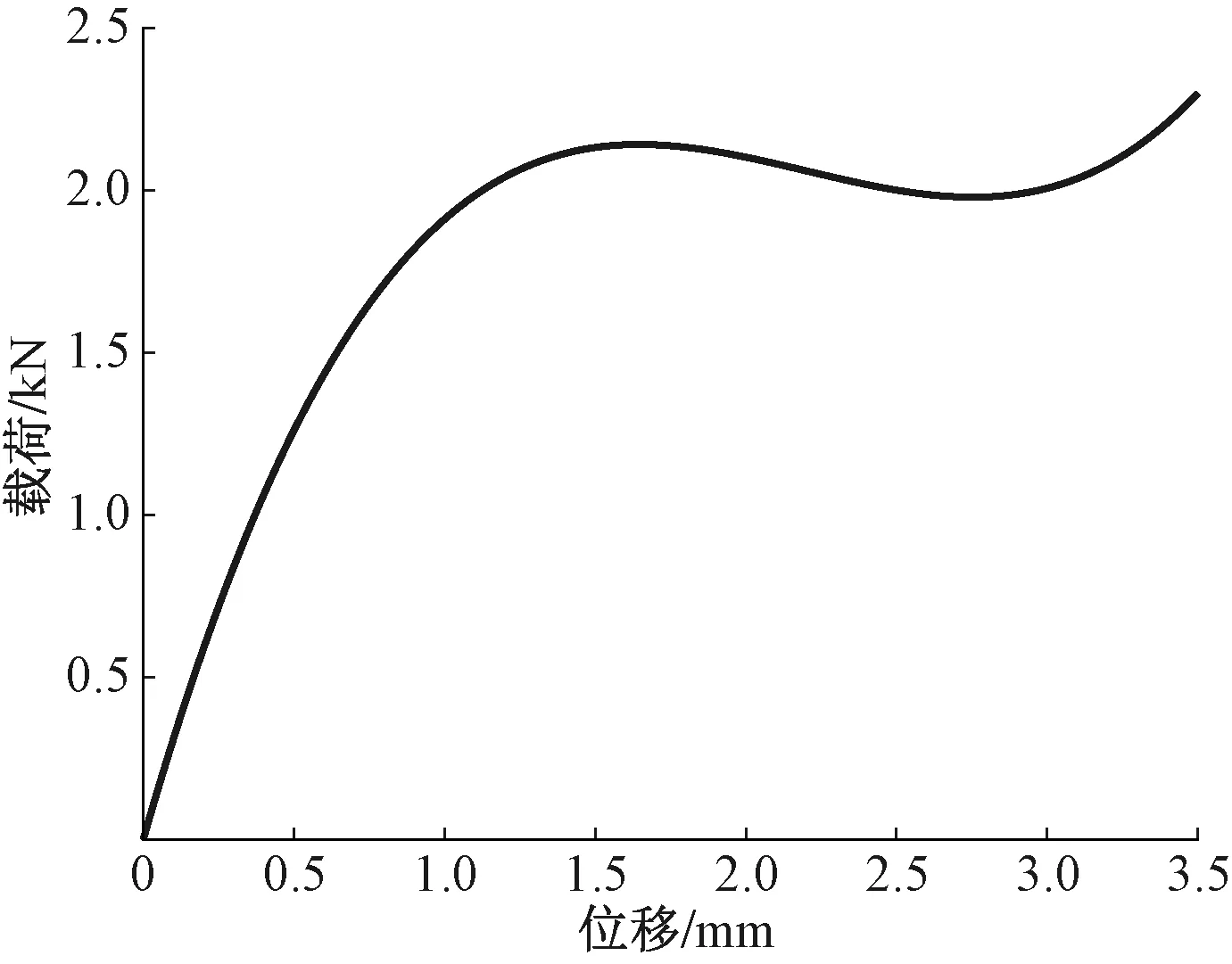
图8 单片碟簧载荷-位移曲线Figure 8 Single disc spring load-displacement curve

由图1可知，准零刚度隔振器受到载荷时，隔振器的回复力Fqzs由螺旋弹簧与碟簧的变形共同提供，此时系统的回复力表达式如下：

(13)

式中:Kv为螺旋弹簧的刚度。

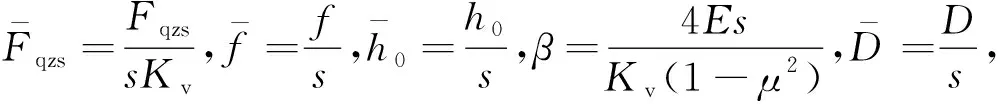
(14)

根据分析，设计一个刚度为200 000 N/m的螺旋弹簧与碟簧并联，构建单个准零刚度隔振器，并将4个准零刚度隔振器嵌入推力轴承，进行推进轴系的纵向隔振。图9为准零刚度隔振器载荷-位移的设计曲线与仿真曲线对比，曲线的吻合度好，因此设计的碟簧与螺旋弹簧并联后，准零刚度隔振器的非线性刚度值能达到预设的1×1012N/m3。

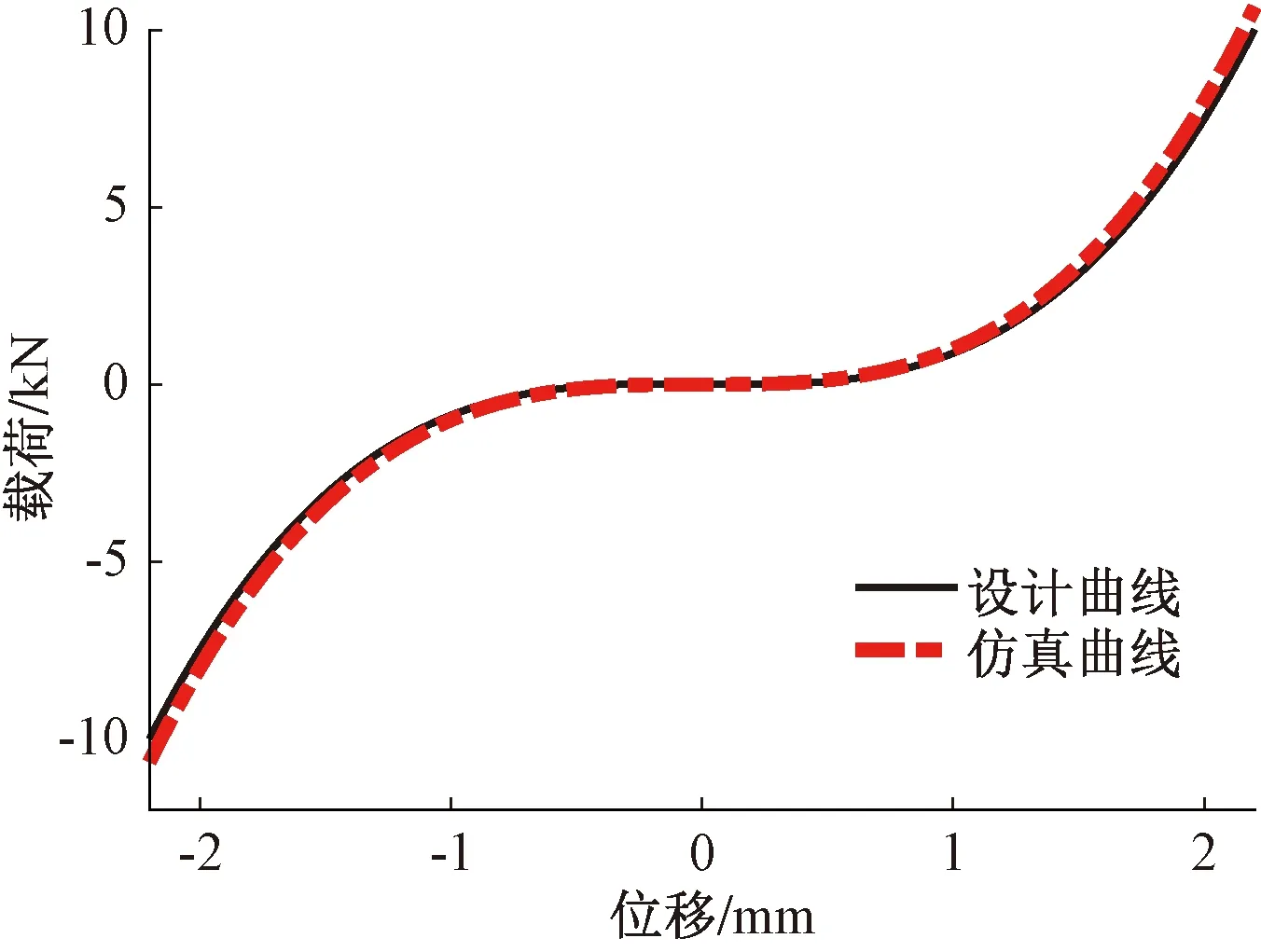
图9 准零刚度隔振器载荷-位移曲线Figure 9 Quasi-zero stiffness isolator load-displacement curve

3.3 阻尼比对系统稳定性的影响

确定非线性刚度参数后，进一步分析不同阻尼比ζ2对系统响应稳定性的影响，如图10所示。图10(a)、10(b)、10(c)分别表示了选取不同阻尼比ζ2时，系统的幅频响应与不稳定区间。图10(d)表示激励力幅值为75 N时，系统的幅频响应随阻尼比ζ2变化的曲线。

由图10可知，阻尼比ζ2越大，系统幅频响应曲线与不稳定区间的交集越小，当阻尼比ζ2取0.05并且激励力幅值小于75 N时，系统的幅频响应曲线不再出现不稳定的区间，这表明此时系统不会出现跳跃现象而影响隔振效果。此外在激励力幅值一定时，增大阻尼比能有效抑制共振峰的峰值，并且降低起始隔振频率。因此选取阻尼比ζ2为0.05。

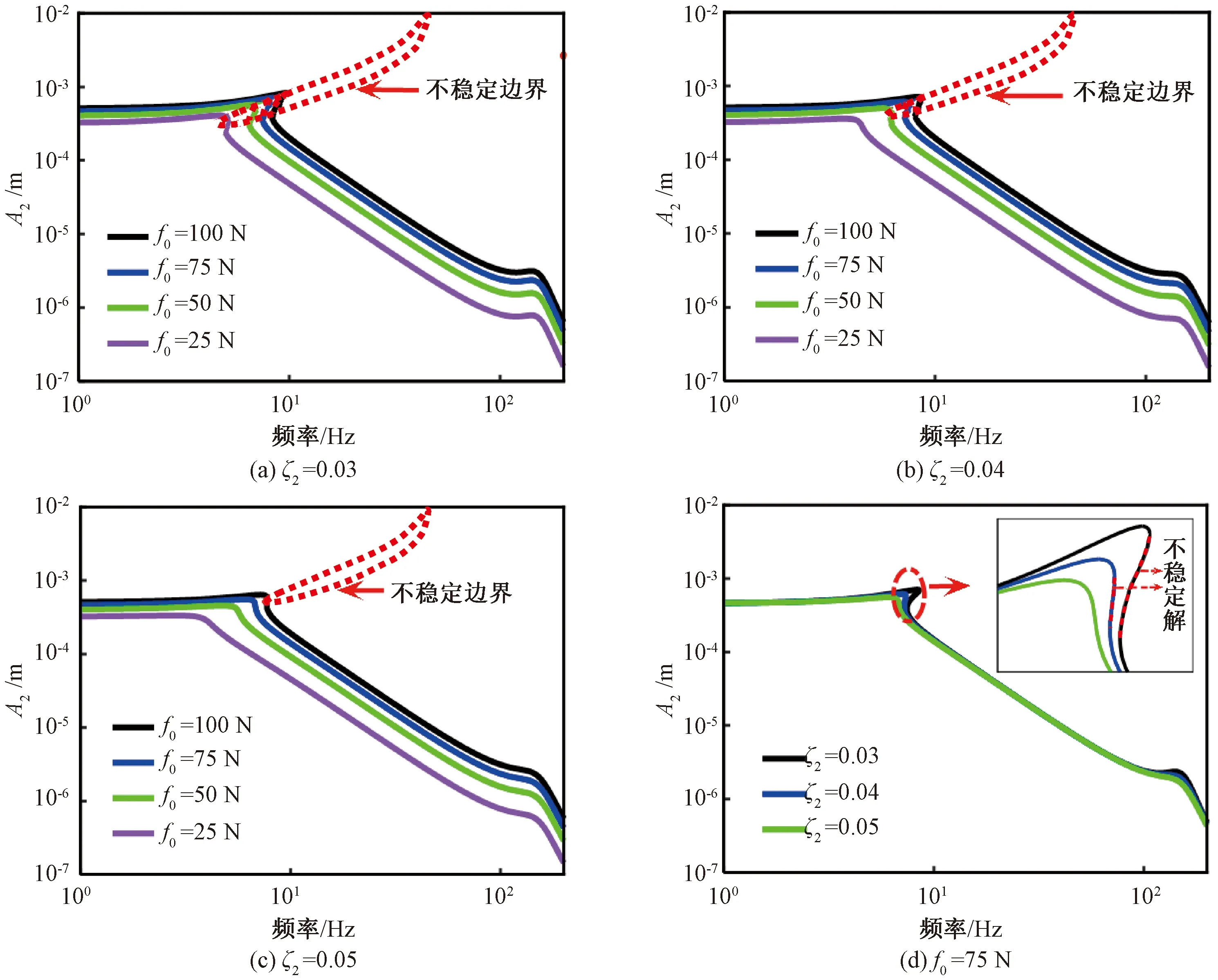
图10 不同阻尼比幅频响应与稳定性图Figure 10 Amplitude-frequency response and stability diagram of different damping ratios

4 隔振性能分析

准零刚度隔振器的非线性刚度与阻尼比分别取1×1012N/m3、0.05时系统的力传递率曲线如图11实线所示，图11中虚线表示无隔振器系统的力传递率。

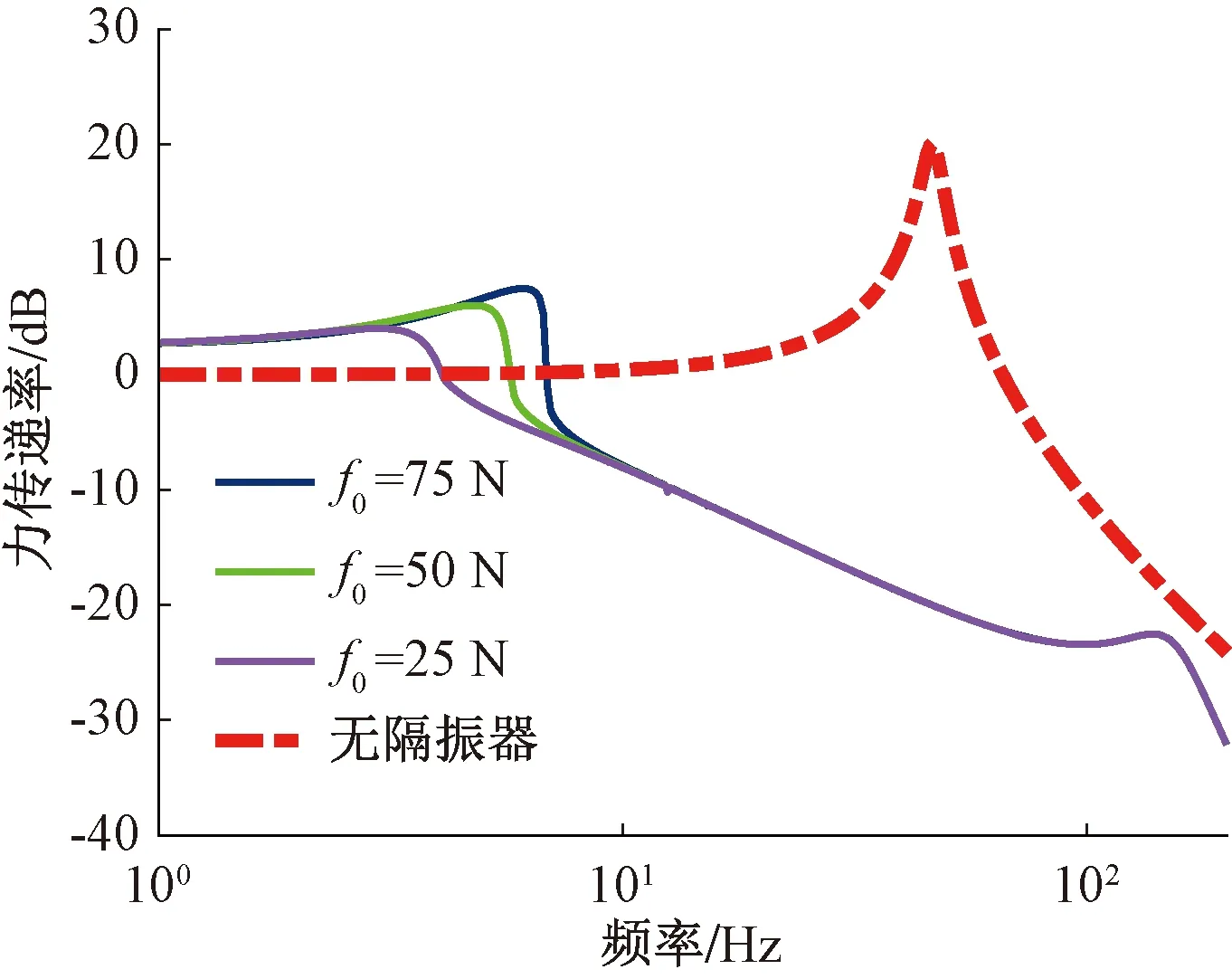
图11 不同激励力幅值条件下系统力传递率曲线Figure 11 System force transmission rate curve in different excitation force amplitude conditions

由图11可知，对于无隔振器的线性系统而言，其力传递率与激励力幅值无关；而对含准零刚度隔振器的系统而言，减小激励力幅值，其力传递率响应峰值与一阶固有频率均减小。将激励力幅值控制在较小范围内时，准零刚度隔振器能够有效隔离10～200 Hz的振动，并且力传递率曲线不再出现跳跃现象。这说明设计的准零刚度隔振器具有高承载、低频隔振性能好的优点。

5 结论

针对船舶推进轴系纵向低频隔振难的问题，将准零刚度隔振器内嵌入船舶的推力轴承。在设计准零刚度隔振器时，综合考虑系统响应的稳定性与轴系纵向静变形的限制，确定了准零刚度隔振器的具体参数。通过静力学分析获得了碟簧与螺旋弹簧相应的结构与力学参数，得出以下结论：当准零刚度隔振器的非线性刚度与阻尼比分别为1×1012N/m3、0.05时，系统稳态响应的解在200 Hz内都是稳定的；在承受10 000 N载荷时，可以有效隔离10～200 Hz的振动。