基于BP与PSO的河口双边界条件逆向推求方法

易 梓 杨，郦 建 锋，钱 进，陆 卞 和，张 语 航，李 丰 铎

(1.河海大学 环境学院，江苏 南京 210098； 2.河海大学 浅水湖泊综合治理与资源开发教育部重点实验室，江苏 南京 210098； 3.中国电建集团华东勘测设计研究院有限公司，浙江 杭州 311122； 4.浙江省华东生态环境工程研究院，浙江 杭州 311122)

0 引 言

台风期的强降雨与天文潮会给中国东部沿海河口地区带来严重的洪涝灾害，造成大量经济损失[1-2]。为保证河口地区的防洪安全，水利部门经常会采用数学模型来预测河口地区的水文过程。MIKE 11模型以其简单干净的数据处理界面、可靠的边界条件输入、模拟板块的多样化等特点在水文模拟中被广泛应用[3-5]。在河口地区水文模拟的过程中，一般是以上游流量和下游潮位为出发点，探究双边界条件对河口地区的影响[6-9]，而以限制河口计算区间某一断面水位为出发点，逆向推求双边界(上游流量、下游潮位)条件的研究较少。然而在逆向推求河口双边界条件时，基于MIKE 11软件的传统试算法是通过手动调节双边界条件来完成该任务，搜索随机性、效率、时间成本成为传统试算法亟待解决的问题。

反馈式神经网络模型，即BP(Back Propagation)神经网络模型是最成熟及应用范围最广的人工神经网络模型，适合解决模拟软件计算效率低的问题[10]。粒子群优化(Particle Swarm Optimizer，PSO)算法是一种新型的全局随机优化算法，其优点是结构简单、全局搜索能力强、鲁棒性好、易于实现和优化效率高[11]。BP神经网络和PSO算法以其网络结构优良和搜索效率高在各种复杂的优化问题中得到广泛应用。例如，赵文刚等[12]基于BP神经网络与PSO算法通过相关性分析和因子贡献率分析，建立西洞庭湖南咀水文站月平均径流预报模型，实现了在保障拟合精度的前提下确定影响径流预报因子最少个数，相比于传统试算法，提高了计算效率；何胜男等[13]以调蓄池截污总量最大为优化目标，以污水处理厂处理规模和可用征地为约束条件，耦合BP神经网络与PSO算法推求各调蓄池的优化截污率，实现了满足占地面积和污水处理厂处理规模下的截污效率最大化，极大节约了计算时间。

本文基于BP神经网络与PSO算法，提出一种在河口某一断面水位确定条件下逆向推求双边界(上游流量和下游潮位)条件的优化方法，并以晋江河口为例，将该方法的计算结果与传统试算法的计算结果进行对比分析。

1 传统的河口双边界条件逆向推求过程

MIKE 11水动力模型由于特有的数据输入格式与数据集成平台的限制，只能根据输入边界得到输出结果，为得到河道水位首先需要将上、下游边界的数据修改成MIKE 11可识别的dfs0时间序列文件，然后将时间序列文件导入MIEK 11的边界文件，最后运行模型得到河口沿程水面线计算结果文件[14-16]，计算效率较低。

因而，以河口某一断面限制水位为约束条件，采用传统试算法逆向推求双边界条件，首先需确定河口下游高潮位，接着根据下游高潮位对上游最大流量不断地进行调整，并且在MIKE 11模型中一一计算，直到求得满足该断面水位条件的上游最大流量，最后输出上游流量、下游潮位双边界条件，具体计算流程如图1所示。由于下游高潮位是一个变化的区间，因此试算法需要根据下游高潮位的变化反复调整上游最大流量，搜索效率低，灵活性较差。

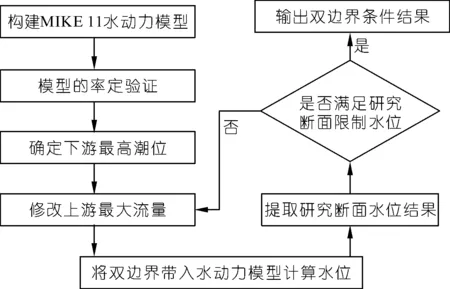
图1 传统试算法逆向推求河口双边界条件流程Fig.1 Flow chart of traditional trial algorithm for inverse derivation of estuarine double boundary conditions

2 基于BP神经网络和粒子群优化算法的河口双边界条件逆向推求过程

MIKE 11水动力模型从输入双边界条件到输出某一断面水位结果是一个繁琐的过程，因此采用BP神经网络建立输入双边界条件与某一断面水位的非线性映射关系。非线性映射关系建立后，从边界条件输入到水位结果输出的时间大大减少。同时为了改进试算法手动修改边界、手动计算不同工况等重复性工作，引入粒子群优化算法，以某一断面水位为优化目标，根据下游高潮位的变化自动搜索上游最大流量进而提高搜索效率。

2.1 BP神经网络建立输入与输出的非线性映射关系

BP神经网络是人工神经网络的一种，主要由输入层、隐含层和输出层组成，具有多层前馈网络和误差反向传播的学习机制[17-18]，图2为建立的河口双边界与某一断面水位的BP神经网络结构图。BP神经网络具有高度的非线性映射能力和较强的泛化能力，其基于梯度下降法原理，预测精度高[19-20]。只要隐含层和隐节点足够多，可以以任意精度逼近一个非线性映射关系[21]。

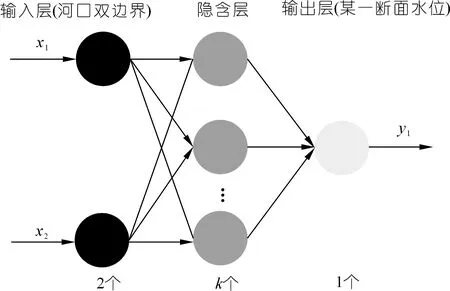
图2 BP神经网络模型结构Fig.2 Diagram structure of BP neural network model

BP神经网络结构的拟合精度受样本数量和样本代表性的影响。样本数量根据实际情况确定。为提高样本数据的代表性，对双边界条件采用拉丁超立方抽样的方法，防止抽取数据过于集中[22]；接着将抽取的样本用MIKE batch模块并行计算；最后利用MATLAB提取指定断面的水位结果，进而得到双边界条件和指定断面水位的离线数据库。

BP神经网络的训练函数选取的是L-M(Levenberg-Marquardt)算法的training函数，设置BP神经网络学习率μ，训练误差为δ。将离线数据库分为训练集和验证集。BP神经网络结构的建立分为两部分：① BP神经网络的训练。通过BP神经网络各层之间的权值与阈值，不断调整训练集中预测输出与期望输出的偏差，直到误差小于预设值δ，训练结束。② BP神经网络的验证。将验证集的双边界条件带入BP神经网络得到预测输出，对比预测输出与期望输出的差异以评价网络结构的优良性。采取MSE(均方误差)、R2(相关系数)来评判BP神经网络的拟合效果。

2.2 粒子群优化算法实现河口双边界条件的逆向推求

根据BP神经网络建立的河口双边界条件与指定断面水位的映射关系，引入粒子群优化算法，实现对边界条件的自动搜寻，提高搜索效率[23-24]。PSO是科学家研究鸟类捕食行为而得出来的一种算法结构，其原理为：PSO初始化为一组随机粒子(随机解)，在每次搜寻过程中粒子通过两个极值(Pbest，Gbest)来更新自己的位置[25]，各个粒子根据对比自身最优解与群体最优解来调整自己的位置和速度，直至到达预设的精度或者预设的算法迭代次数[26]。

通过对PSO变量中初始种群数、学习因子、迭代次数以及对河口某一断面水位(优化目标)的设定，构建PSO算法结构。设置河口某一断面水位为优化目标，初始化的粒子随机分布在样本空间中，粒子不断调整自身空间位置以搜索满足优化目标的最优解。

2.3 优化方法与传统试算法对比

图3为优化方法与传统试算法的计算流程对比图。优化方法相比于传统试算法，主要从两个方面进行了改进：① 基于BP神经网络构建河口双边界条件与某一断面水位的非线性映射关系，从边界条件的输入到断面水位结果的输出只需要几秒，提高了传统试算法的计算效率；② 基于粒子群优化算法，通过优化目标的设定，实现双边界条件的自动搜索，提高了传统试算法的搜索效率。

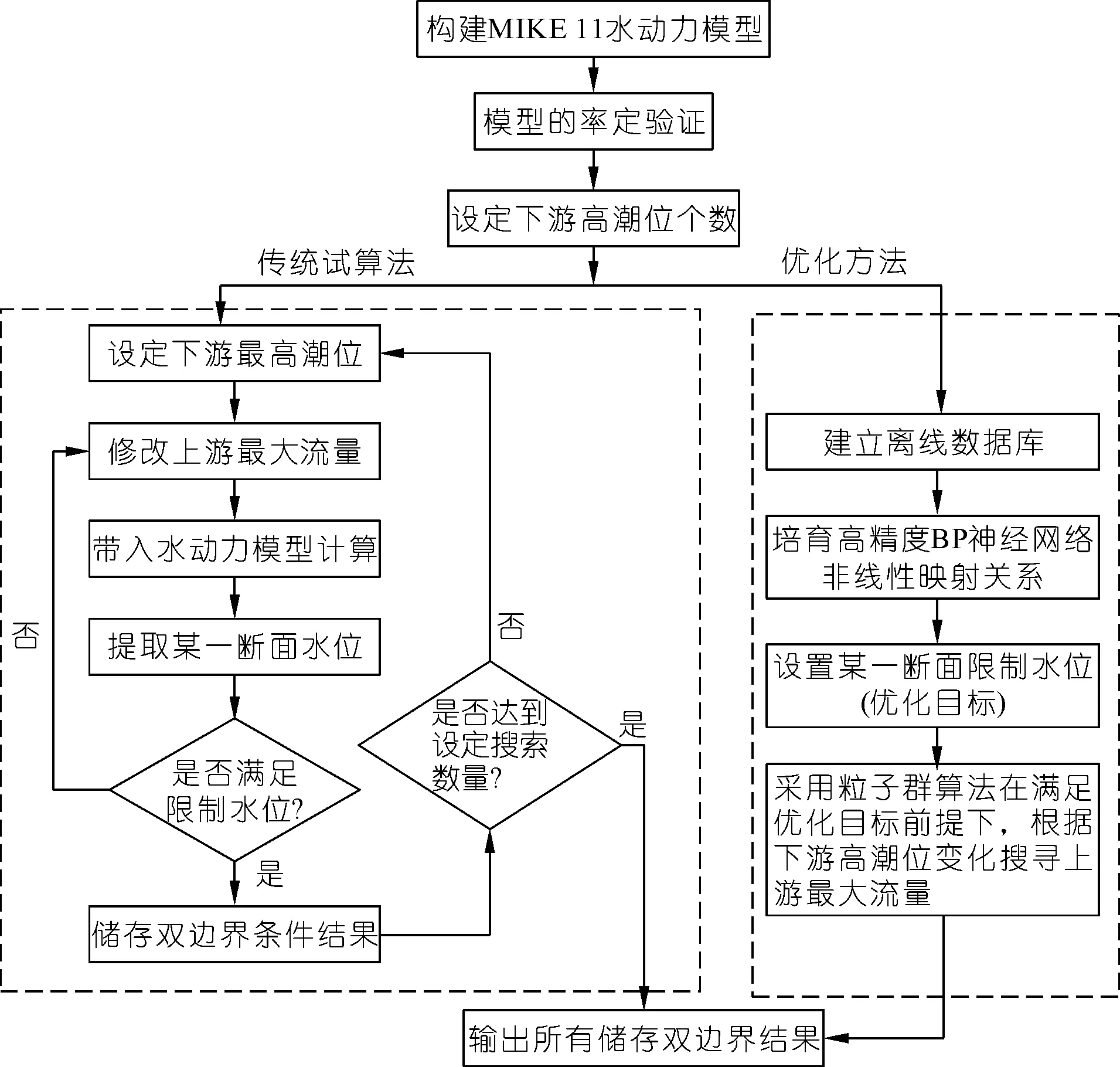
图3 优化法与传统试算法计算流程对比Fig.3 Comparison of the calculation processes of the optimization method and the traditional trial method

3 实例应用

3.1 研究区域概况

晋江位于福建省东南沿海，是中国台风登陆的主要路线之一，台风活动极为频繁，多发生在7～9月。如遭遇天文大潮，其危害性更大。晋江作为主要的泄洪通道，在雨水频繁期，承载着巨大的泄洪压力。查阅晋江水文资料，金鸡水闸100 a一遇的洪峰流量为11 100 m3/s；前浦站100 a一遇的最高潮位为5.16 m，多年平均最高潮位为4.00 m。本次研究范围从金鸡水闸到前浦站，共19.30 km，具体如图4所示。

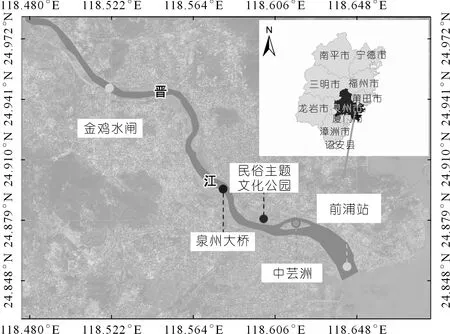
图4 研究区域概况Fig.4 Overview of the research area

为了保证晋江河口两岸人民的安全，需要限制防洪安全空间不足地区的最高水位。根据福建省水利水电勘测设计研究院2020年编制的《晋江下游防洪标准复核报告》可知，晋江河口地区民俗主题文化公园处的防洪措施最为薄弱。在100 a一遇洪水和100 a一遇潮位的情形下，民俗主题文化公园处计算水位为7.832 m。为了给民俗主题文化公园预留足够的防洪空间，本文以民俗主题文化公园水位6.832 m为优化目标，对双边界条件进行逆向推求。

3.2 水动力模型构建

以MIKE 11为计算平台，对研究区域建立水动力模型，概化河长为19.30 km，从金鸡水闸到前浦站，共概化断面55个。为保证模型计算时的稳定性，根据河道水位的实测值，设置初始水位为2.00 m。

泉州大桥(桥下)水位站为国家基本水文站，有逐日水位观测数据。晋江下游沿程设有水尺，自动化记录水位数据。2016年9月15日为晋江下游近年来最大洪水，2019年6月3日为当年最大洪水，根据水文站及水尺的记录数据，采用2016年9月14～16日测量水位数据对建立的水动力模型进行率定，选择2019年6月2～5日测量水位数据对率定的水动力模型进行验证。模型率定的结果表明：河道主槽糙率在 0.036～0.040之间，滩地糙率在0.042～0.050之间。模型验证的结果表明：河道沿程水位的实测值与计算值拟合较为良好，水位绝对误差小于5 cm(见表1)；泉州大桥(桥下)水位站实测水位与计算水位的绝对误差小于8 cm(见图5)。水利部颁布的SL 483-2017《洪水风险图编制导则》[27]规定，水位允许绝对误差不应超过20 cm。因此，本文建立的水动力模型的精度满足实际应用需要。

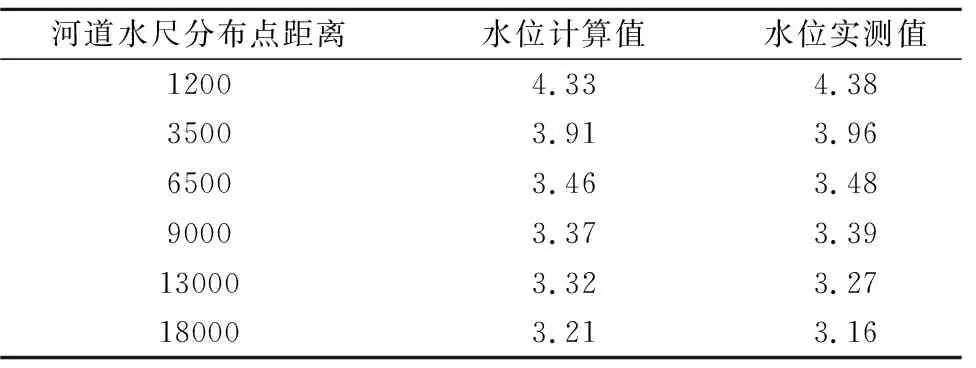
表1 沿程水位计算值与实测值比较Tab.1 Comparison of calculated and measured values of water levels along the course m

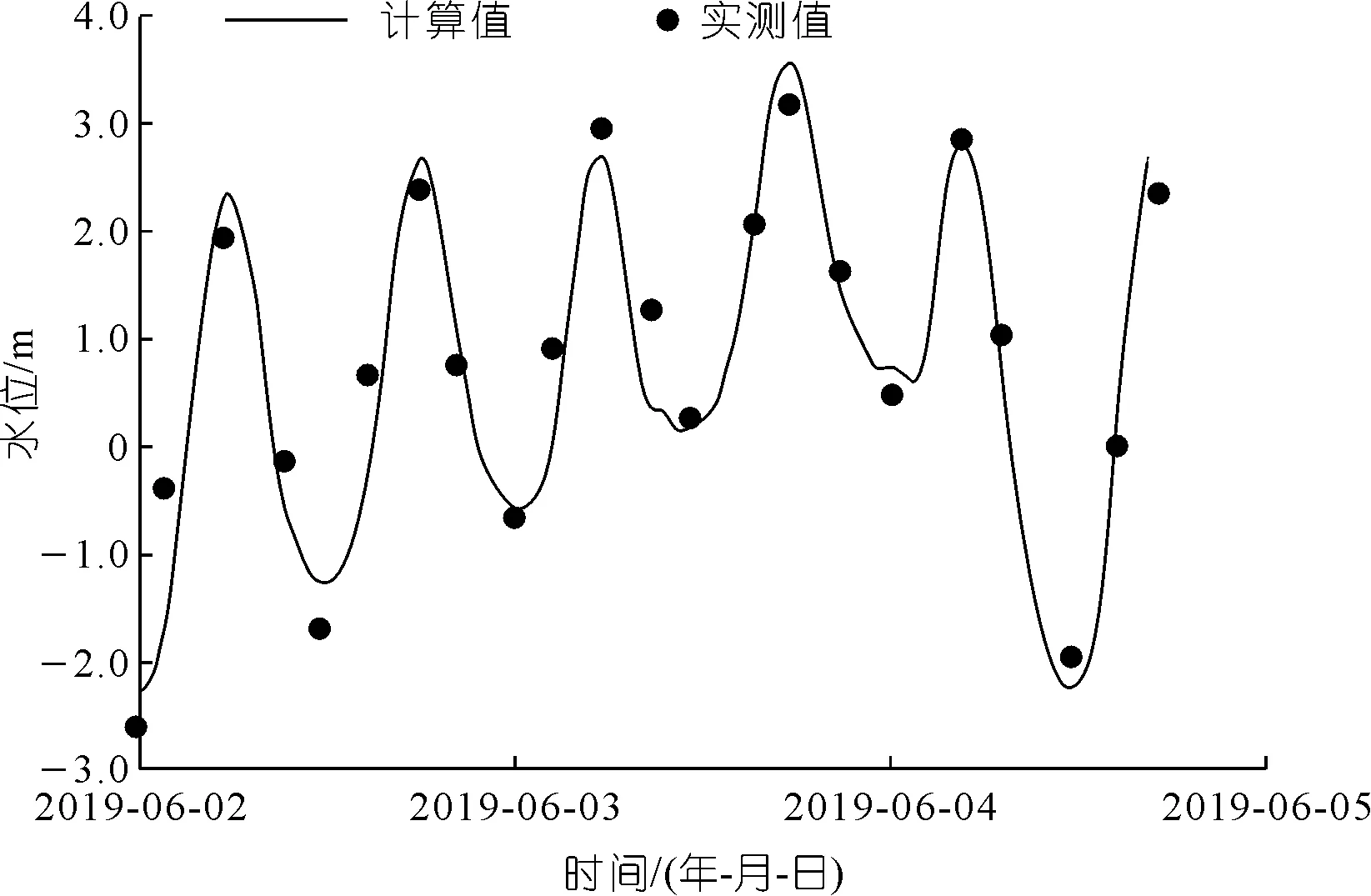
图5 泉州大桥(桥下)水位站水动力模型验证结果Fig.5 Hydrodynamic model validation results of Quanzhou Bridge (under bridge)water level station

3.3 计算结果

3.3.1传统试算法计算结果

为了保证民俗主题文化公园最高水位小于6.832 m，通过已率定验证后的MIKE 11水动力模型逆向推求上游流量和下游潮位边界条件。选取前浦站100 a一遇最高潮位5.16 m、50 a一遇最高潮位5.04 m和多年平均高潮位4.00 m为典型情况逆向推求上游最大下泄流量。逆向推求过程及结果如表2所列。为保证民俗主题文化公园处于防洪安全位置，下游最高潮位为5.16 m时，上游最大流量为8 160 m3/s；下游最高潮位为5.04 m时，上游最大流量为8 300 m3/s；下游最高潮位为4.00 m时，上游最大流量为9 210 m3/s。由表2可以看出，试算法计算精度有限，随机性大，花费的时间长，搜索效率较低。

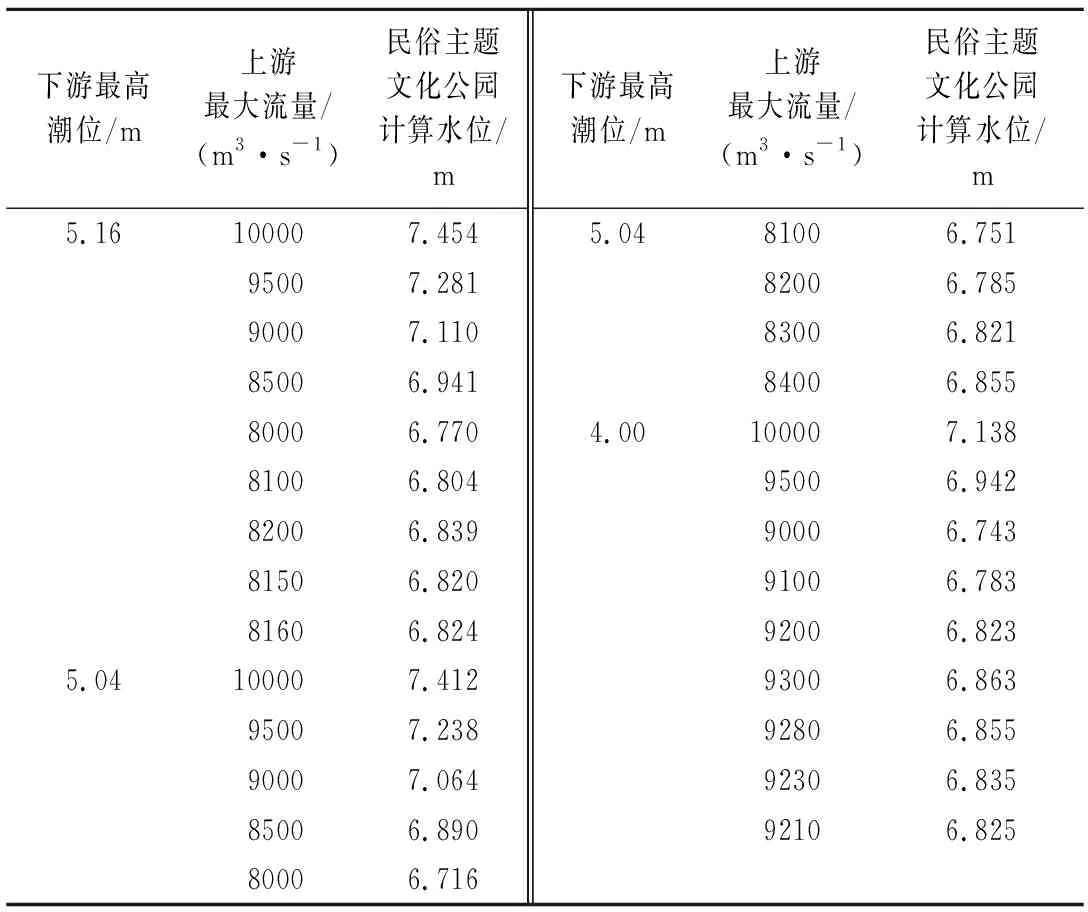
表2 传统试算法逆向推求双边界条件结果Tab.2 Results of traditional trial algorithm for inverse derivation of double boundary conditions

3.3.2优化方法计算结果

根据晋江水文资料，选取100 a一遇最高潮位与多年平均潮位作为潮位样本空间最大值与最小值，选取100 a一遇最大洪峰流量作为流量样本空间的最大值，流量样本空间在不影响计算效率的同时应尽可能广，以对应下游潮位的变化，根据计算设定流量样本空间的最小值为7 000 m3/s。因此设置样本空间为上游最大洪峰流量7 000～11 100 m3/s，下游最高潮位为4.00～5.16 m。利用拉丁超立方抽样在区间范围内抽取1 000 组上、下游边界，然后采用MIKE batch模块将得到的1 000组边界数据进行并行计算，利用MATLAB批量提取民俗主题文化公园水位结果，进而建立双边界条件与民俗主题文化公园水位的离线数据库。基于MATLAB平台搭建BP神经网络，具体参数设置为：输入层2个，隐含层9个，输出层1个，迭代次数1 000 次，学习率0.001，训练误差达到10-6级。

选取750组数据作为训练集，250组数据作为验证集。BP神经网络预测水位输出结果与期望水位输出结果如图6所示，MSE=1.36×10-6、R2为0.996。由此判断BP神经网络拟合效果较好，预测精度高。

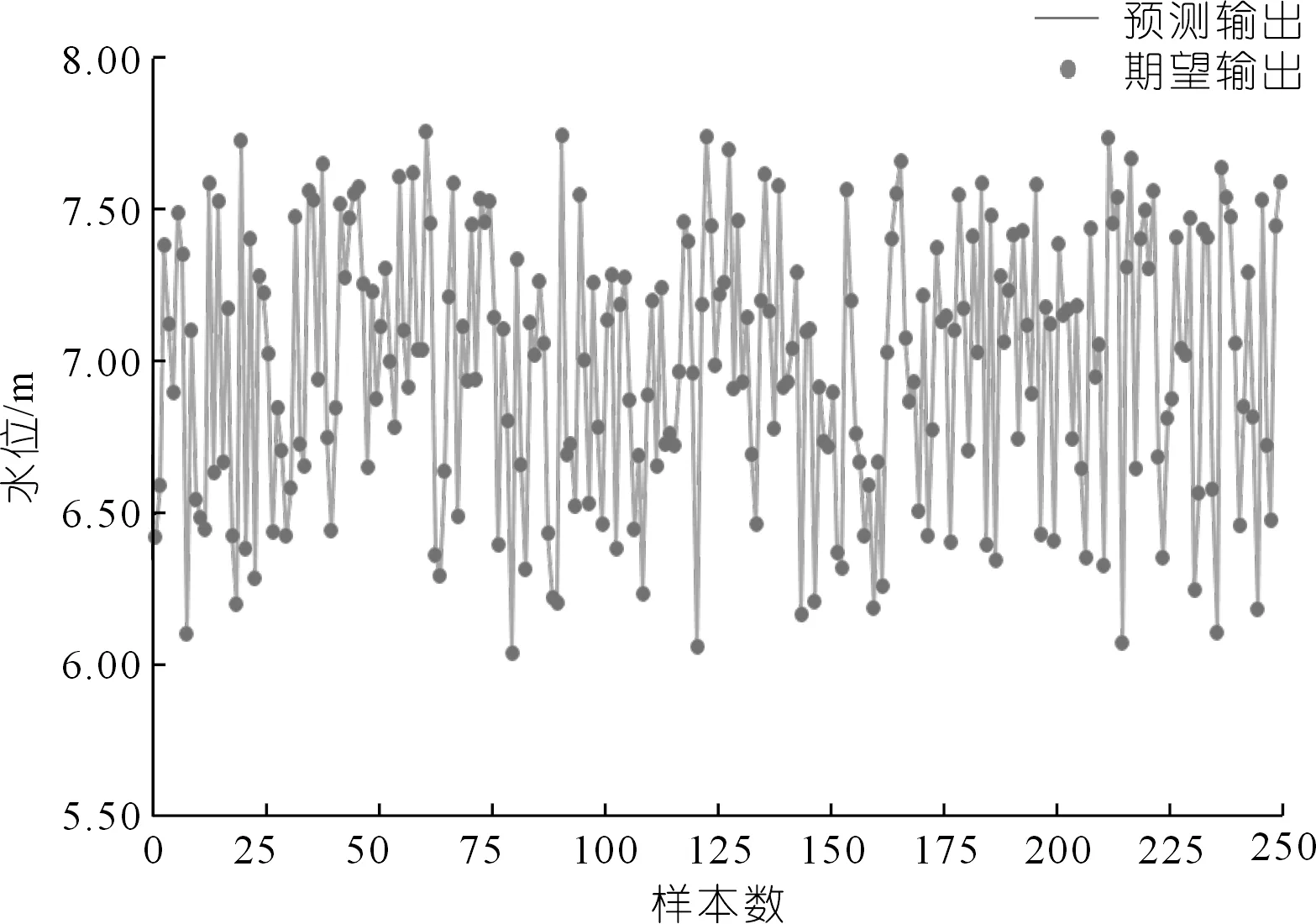
图6 BP神经网络预测输出与期望输出水位对比Fig.6 Predicted output versus desired output water level by BP neural network

粒子群优化过程中，惯性权重C1=0.8，自我学习因子C2=2.0，群体学习因子C3=2.0，迭代次数为400次，种群规模为30。搜索空间为上游最大流量7 000～11 100 m3/s，下游最高潮位4.00～5.16 m。潮位搜索间隔为0.04 m，总共29种工况。

以民俗主题文化公园最高水位6.832 m为优化目标，逆向推求满足优化目标的双边界条件映射关系。计算得到的上游最大下泄流量与下游高潮位之间映射关系如图7所示。根据PSO算法计算结果，在100 a一遇最高潮位为5.16 m时，上游最大下泄流量为8 181.00 m3/s；在50 a一遇最高潮位为5.04 m时，上游最大下泄流量为8 332.51 m3/s；在多年平均最高潮位为4.00 m时，上游最大下泄流量为9 222.72 m3/s。对上游最大下泄流量随下游高潮位的变化关系选择二次函数进行拟合，x为下游高潮位，y为上游最大下泄流量。最终拟合公式为y=6195.1091+2028.2287x-318.2523x2，R2计算值为0.999 87，拟合效果较好。拟合公式可以很好地反映上游最大下泄流量随下游最高潮位的变化情况，可为晋江金鸡水闸的调度提供依据。根据下游潮位的变化，金鸡水闸可相应调整最大下泄流量，以保证民俗文化主题公园处于防洪安全空间，实用参考性强。

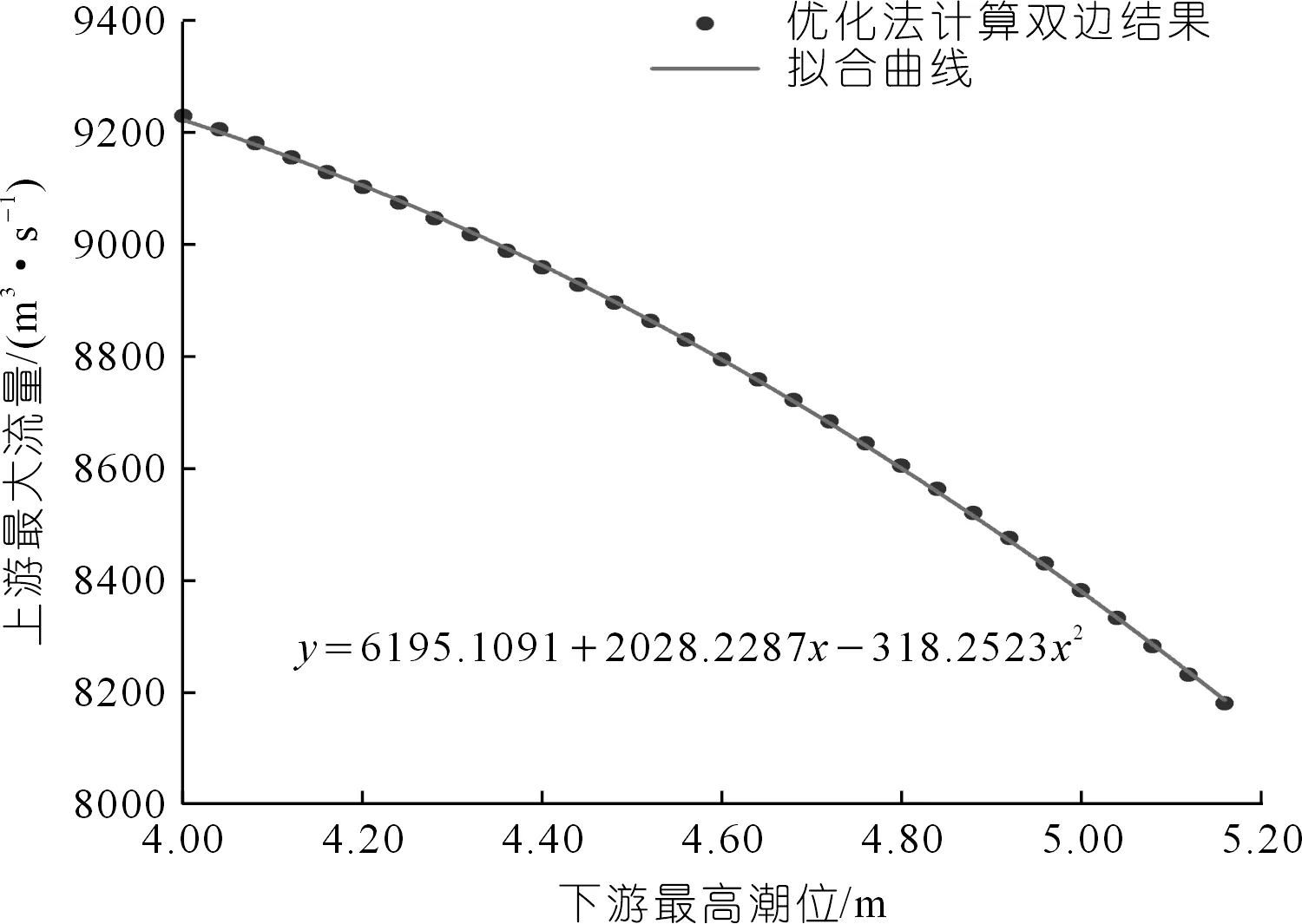
图7 上游最大下泄流量随下游最高潮位变化Fig.7 Variation of upstream maximum flow with downstream maximum tide level

3.4 对比分析

选取下游最高潮位为100 a一遇、50 a一遇和多年平均3种典型情形进行计算，传统试算法与优化方法计算结果对比如表3所列。在3种情形下，传统试算法计算民俗主题文化公园水位与目标水位均存在一定偏差，但优化法计算水位与目标水位一致，在计算精度上优化法略大于传统试算法；传统试算法推求过程中实验次数随机性强，需要人工操作时间长，逆向推求一组满足优化目标的双边界条件所需时间约为10 min，优化方法逆向推求一组满足优化目标的双边界的时间约为1 min，在计算效率上优化法相比于传统试算法提升了约10倍。因此，优化方法计算精度和计算效率均优于传统试算法，更适合解决河口地区双边界的逆向推求。

表3 传统试算法与优化法计算结果对比Tab.3 Comparison of the results of the traditional trial method and the optimization method

4 结 语

本文为解决传统试算法逆向推求河口双边界条件(上游流量、下游潮位)计算效率与搜索效率低、时间成本高的问题，提出基于BP神经网络与PSO算法逆向推求边界条件的优化方法。研究表明：基于BP神经网络与PSO算法的优化方法相比于传统试算法，在保障计算精度的前提下，计算时长约减少至原来的十分之一。优化方法科学、高效且适用范围广，更适合河口地区双边界条件的逆向推求，同时可为河口地区防洪调度提供技术支持。