水电站生态机组装机容量确定方法研究

范 仕 虎，杨 曼，王 朋

(1.河南省水利第二工程局，河南 郑州 450016； 2.郑州大学 水利科学与工程学院，河南 郑州 450001； 3.河南郑大水利科技有限公司，河南 郑州 450001)

0 引 言

由于历史原因，中国大部分小水电在建设规划时未充分考虑对河流生态的影响，导致其机组与河流生态流量匹配性差，尤其是河床式或坝后式水电站，在机组正常运行发电时，发电用水基本可以满足下游生态流量要求，而在来流较小时段，机组不开机运行，下游河流则处于脱流状态，无法满足生态要求[1-2]。随着绿色小水电的持续推进，国家和地方前后出台多项政策，明确要求强化小水电生态流量的泄放、监督和管理，以保障河流的生态功能要求[3-4]。对于小水电而言，装设生态机组实现生态流量的持续下泄，是常见的绿色电站改造方案。

对于改造的河流生态电站，合理确定其装机容量是关键。朱蒙恩[5]提出将生态流量作为生态机组的额定流量确定装机容量；吴文涛等[6]提出将生态流量作为生态机组最大发电水头对应的流量，以此确定装机容量；彭小东等[7]提出将生态流量作为生态机组任一运行工况下均能达到的流量，并结合水头变化确定装机方案。上述生态电站装机方案通过生态流量确定生态电站装机容量，在进行装机容量确定时，未充分考虑不同装机方案在发电效益、机组利用效率、弃水、投资等方面的优劣，装机容量的确定未充分反映生态电站的不同目标的需求，存在一定的局限性，无法有效指导生态电站装机的确定。

层次分析法是一种层次权重决策分析方法，能够通过对多指标决定的问题进行分析，以优先等级的形式对备选决策进行排序，适用于解决难以定量分析、多目标、多准则等复杂决策问题。基于此，本文引入层次分析的方法，通过生态流量初选装机方案，选择发电效益、机组利用效率、弃水和投资4部分作为目标层，构建生态电站装机方案的层次分析模型，通过模型求解，实现生态电站装机方案的最优确定。

1 河流生态流量计算方法

随着河流生态保护理论的发展，河流生态流量的计算方法也日益丰富。目前，生态流量的计算方法大致可以分为：水力学法、历史流量法、栖息地定额法、整体分析法[8-10]；为了从不同角度反映河流对生态流量的需求，本文选择不同规则下的生态流量计算方法，通过对不同计算方法进行筛选对比，最终确定合理的河流生态流量值。本文在计算河流生态流量时，采用年内展布计算法、Tennant法以及7Q10法进行分析计算：

(1) 年内展布计算法。该算法基于历史径流资料，以年最小径流总量与多年平均径流总量二者之间的比值，得到各月生态流量与各月多年平均径流量之间的关系，以此来确定生态流量。

(2) Tennant法。该方法不需要河流的地形地质资料，也不需要河流生物环境资料，仅根据水文径流资料，即可进行生态流量的估算[9]。在计算时，以河道多年平均径流量作为基础，根据设定的需水情况以及来水情况，选取一定的频率计算得到河道生态流量。

(3) 7Q10法。对于河流最小流量的设计值，国外通常采用90%的保证率连续最枯7d的平均流量，中国通常采用最近10 a最枯月平均流量或者90%的保证率最枯月平均流量[10]。采用该算法计算时可以通过采用不同的保证率达到相应的生态标准。

2 河流生态流量与装机容量确定的关系

生态电站多根据现有建筑物增设生态机组，当站址确定后，可以认为机组的水头已经确定，其装机容量可以近似与其可用流量有关。考虑生态流量一般较小，电站原机组装机容量较大，为了匹配较小流量，一般仅设置一台小机组作为生态机组进行流量匹配[5-7，11]。生态流量Q可以作为该生态机组的最小开机流量、保证流量、设计流量，分析河流生态流量与装机容量确定关系如下：

(1) 作为机组最小开机流量。当河流生态流量作为机组最小开机流量时，机组设计流量Qs会明显大于Q，机组可以充分利用生态流量以上流量；对于生态泄流大于生态流量Q时，机组仍可以开机运行，且效率提高，适用于水量充沛、生态流量长期处于较高水平的河流；但当河流按照生态流量下泄时，电站虽然可以开机运行，但机组运行效率较低。

假定机组设计流量为

Qs=aQ

(1)

则电站的装机容量为

N=KQsH=aKQH

(2)

式中：K为综合出力系数，可依据相关规范标准或设计手册进行选择；Qs为机组设计流量；H为发电净水头；Q为机组最小开机流量，也即河流生态流量；a为大于1的计算参数，与机组运行特性有关，一般可取1.5～2。

(2) 作为机组保证流量。当河流生态流量Q作为生态机组保证流量时，该流量对应的即为生态机组保证出力，由于河流下泄流量均应大于等于河流生态流量Q，因此，河流生态流量Q的保证率为100%；考虑生态机组可利用的流量为区间流量，其设计保证率可小于100%，因此生态电站对应的保证流量Qb应大于等于Q，即：

Qb=bQ

(3)

增设生态电站的装机基本为1台[5-7，11]，其装机容量可确定为：

N=KQbH=bKQH

(4)

式中：Qb为保证流量；b为大于1的计算参数，设计保证率越高，b越接近1，一般可取1.05～1.20。

(3) 作为机组设计流量。当河流生态流量Q为机组设计流量时，此时电站装机容量计算为

N=KQH

(5)

对上述3种方法进行对比评价，结果如表1所列。

表1 不同装机确定方法的对比Tab.1 Comparison of different determination methods

3 层次分析法

3.1 模型结构

层次分析法主要涉及系统科学的决策问题，需要将决策问题置于系统中，并将相互影响的因素及问题层次化，形成多层次的分析模型[12]；利用数学分析和定性分析结合的形式进行排序和分层，通过获得每种方案的权重值来指导决策[13-14]。其结构模型如图1所示。

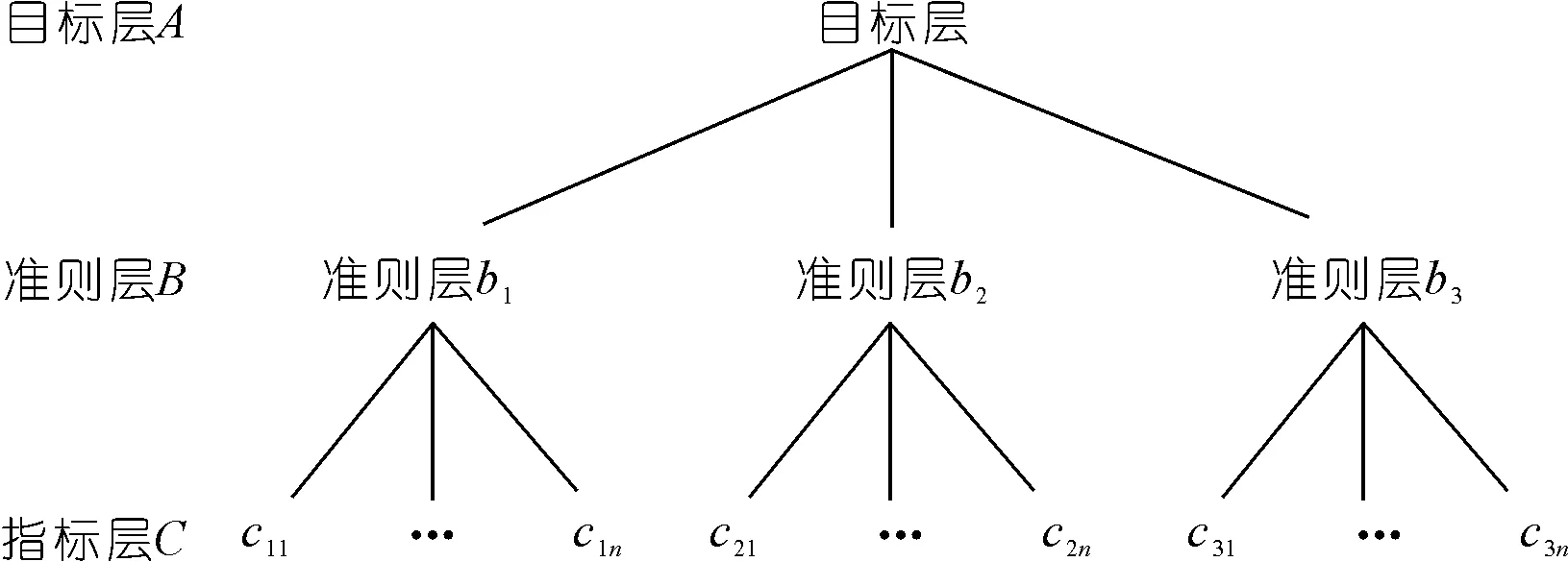
图1 层次分析法结构Fig.1 Structure of AHP

3.2 求解流程

(1) 构造判断矩阵。依据指标层Cij(i=1，2，…n；j=1，2，…，m)对准则层bi(i=1，2，…，n)的重要度，以1～9作为比较的标准，两两进行相比，利用Delphi法给出矩阵的元素值。有关1～9标度及其内容见表2。

表2 判断矩阵(1～9)标度及其内容Tab.2 Scoring and content of judgment matrix

(2) 计算指标权重。设判断矩阵D=dij(i=1，2，…，n；j=1，2，…，m)，则：

(6)

(7)

(8)

w=(w1，w2，…，wn)

(9)

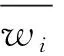
(3) 判断矩阵一致性。

(10)

CI=(λmax-n)/(n-1)

(11)

CR=CI/RI

(12)

式中：λmax为判断矩阵最大特征值；CI为判断矩阵D的一致性指数；CR为随机一致性比率；RI为判断矩阵的随机一致性指标(见表3)[13-14]。

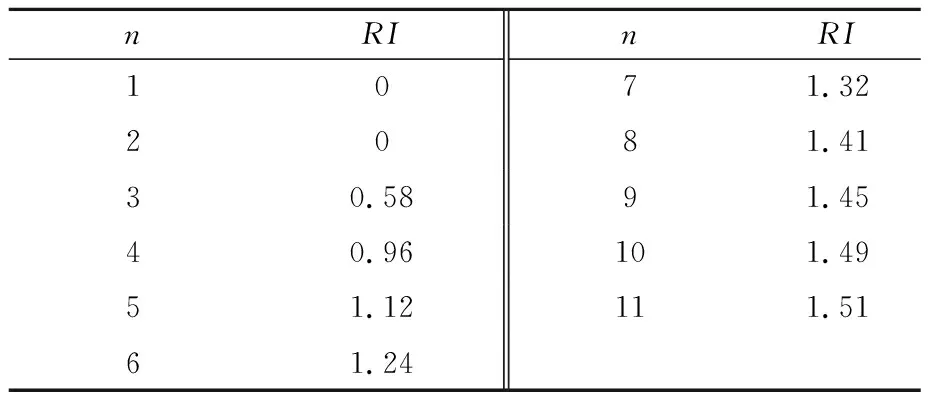
表3 判断矩阵的随机一致性指标Tab.3 Random consistency index of judgment matrix

若CR<0.1，则认为D具有满意的一致性，否则须重新构造D，直至有满意的一致性。

(4) 综合权重的计算。将上述得到的单项权重进行相应组合，得到评价指标对于构造目标层的综合权重。

(13)

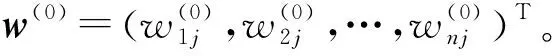
4 实例分析

4.1 基本资料

以汉江支流唐白河流域鱼网系水电站为例开展实例验证。该水电站现有装机为6 000 kW(2×3 000 kW)，设计水头为21 m，机组设计流量为14.57 m3/s，最小开机流量约8.2 m3/s，与河流生态流量不匹配，当需要下泄小于8.2 m3/s时，电站往往不开机运行，造成下游缺水；或虽然开机运行，但电站通过长距离引水渠引水发电，造成河流局部河流段脱水，河流生态遭到破坏，生态流量不能保障。针对现有问题，拟在原电站引水渠渠首处增设生态电站，通过新建机组对生态流量进行匹配，考虑该处河流生态流量较小，此次考虑新建1台机组。

河流电站处1965～2018年共54 a的年平均径流量及月平均径流量如图2～3所示。

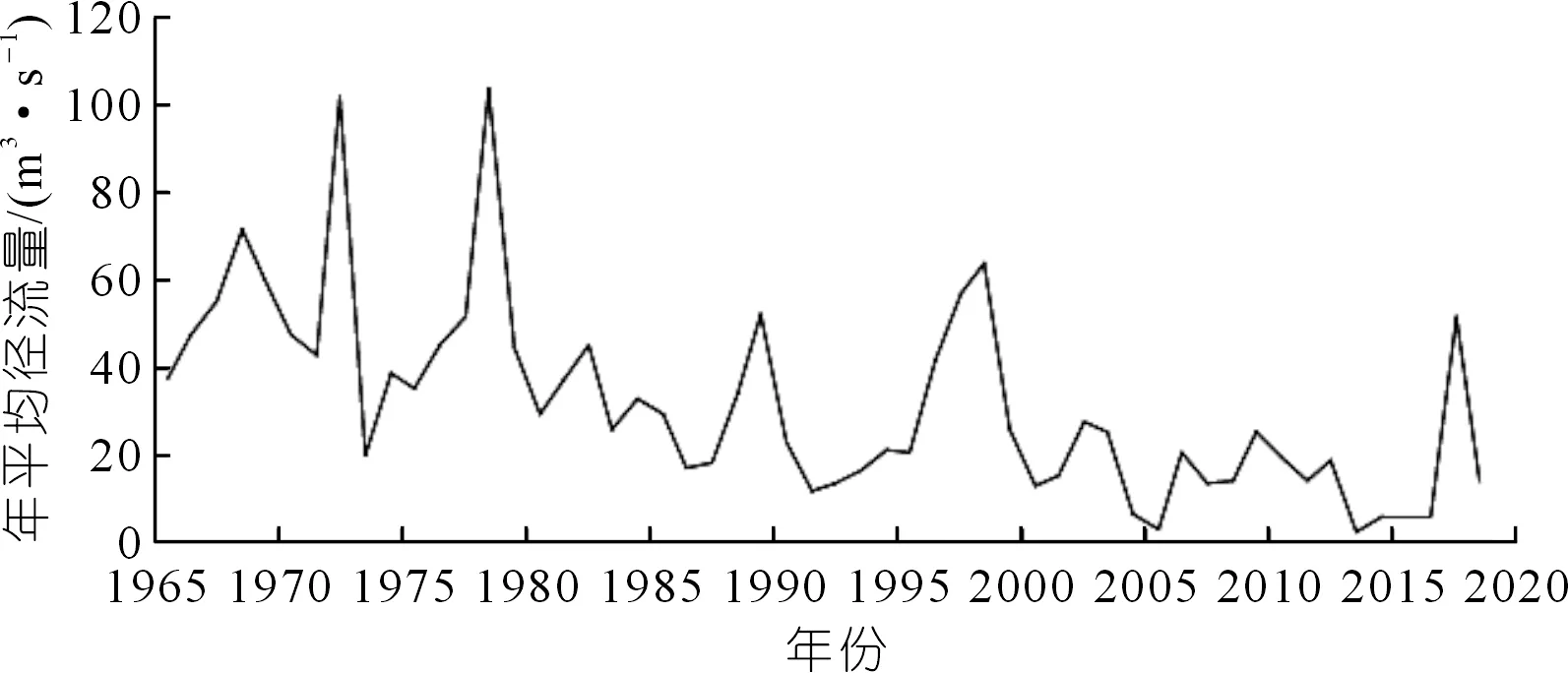
图2 多年平均径流量Fig.2 Average annual runoff

图3 多年月平均径流量Fig.3 Average monthly runoff

4.2 生态流量计算及确定

按照年内展布计算法、Tennant法以及7Q10法分别对河流生态流量进行分析计算，计算结果如表4所列。

表4 河流生态流量计算成果Tab.4 Results of ecological flow by different methods m3/s

通过分析可知，上述3种方法计算的河流生态流量差别较大，其中Tennant法计算的生态流量最大。考虑下游生态环境、河流净化等功能，最终确定河流生态流量按照Tennant法计算，即10月至次年3月份下泄流量为3.19 m3/s，4～9月份下泄流量为6.38 m3/s。

4.3 生态电站装机容量确定

按照本文的3种方法，分别计算装机容量。

(1) 生态流量作为机组最小开机流量。以3.19 m3/s作为机组最小开机流量；此时，装机容量N=a×9.8×21×3.19=a×657 kW；按照21 m水头机型效率曲线，最小开机流量与设计流量比可取1.5～2；按照a=1.8，计算电站装机容量为1 182 kW，按照机组标准图谱，选择1 200 kW装机。

(2) 生态流量作为保证流量。按照设计保证率80%计算，对多年径流资料进行统计，对于10月至次年3月份来流量小于3.19 m3/s，取3.19 m3/s，对于4～9月份下泄流量小于6.38 m3/s取6.38 m3/s；进行统计排频，找出出现频率在80%的流量值为4.76 m3/s，从而得到保证流量，计算装机N=9.8×21×4.76=980 kW，按照机组标准图谱，选择1 000 kW装机。

(3) 生态流量作为机组设计流量。计算装机N=9.8×21×3.19=656 kW，按照机组标准图谱，选择700 kW装机。

4.4 方案对比分析

假定河道按照上述生态流量进行下泄，且所有下泄流量均通过生态电站，按照上节计算得到的1 200，1 000 kW和700 kW 3种方案分别对河流生态电站的发电情况及弃水情况进行分析，如图4～5所示。

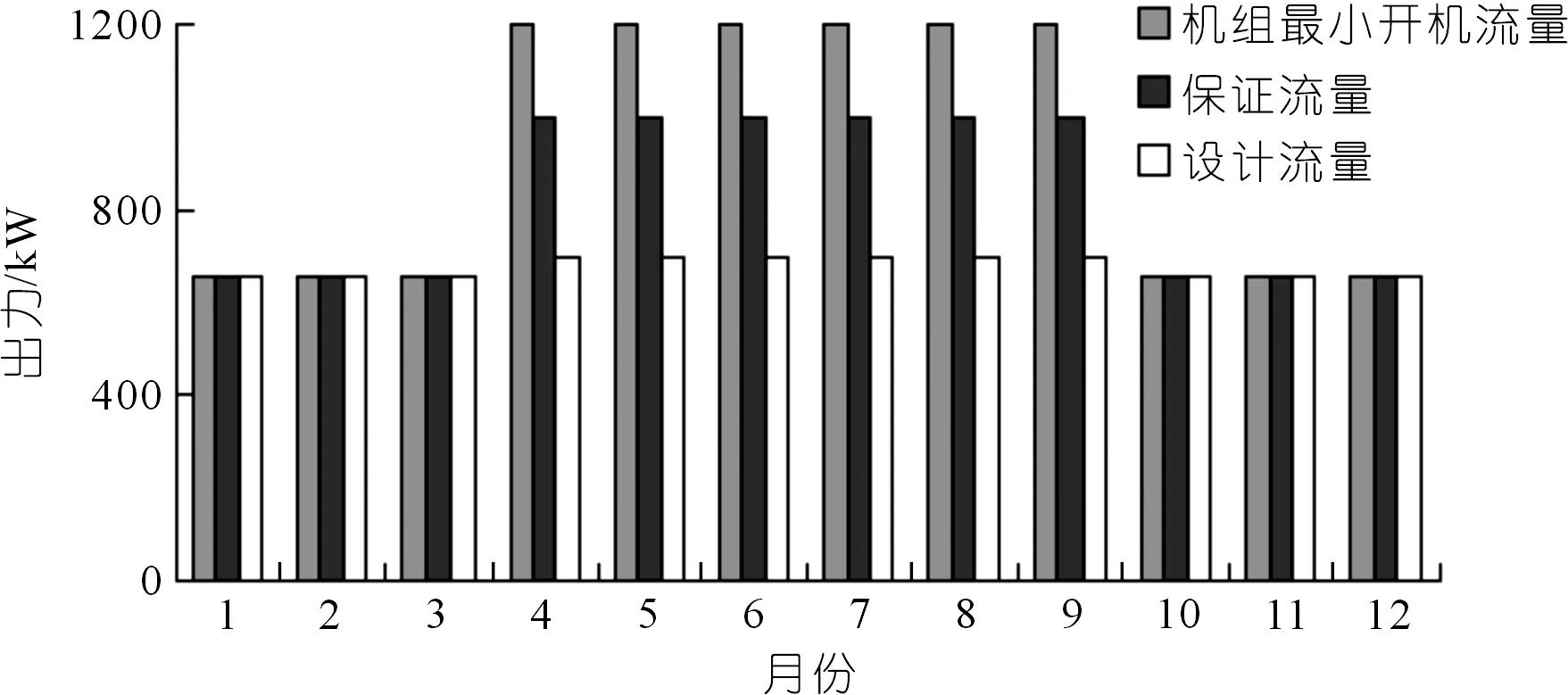
图4 不同方案的出力比较Fig.4 Outputs of diffenent schemes

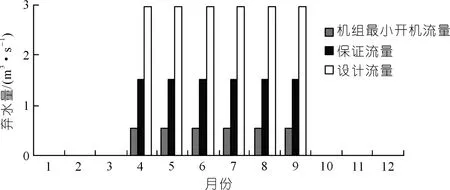
图5 不同方案的弃水比较Fig.5 Abandoned water volumes of different schemes

通过对图4～5进行分析可知，3个方案均可以在4～9月满发，其出力分别可以达到1 200，1 000 kW和700 kW；其弃水均发生在4～9月，弃水流量为0.55，1.52 m3/s和2.98 m3/s。上述3个方案均可以对10月至3月的小流量进行有效利用，而此时1 200 kW机组虽然可以开机，但是其机组效率相对较低；面对大于4～9月的大流量时，其利用程度存在较大的差异。

不同的3个方案均可以满足生态流量的调度，对于发电效益、机组利用效率、投资、施工难度等方面均还存在一定的差异，按照定性分析，对其进行对比，如表5所列。

表5 不同装机方案的技术比较Tab.5 Comparison of the technics of different schemes

4.5 层次分析法

根据上节对不同的方案进行技术比较，拟定生态电站的层次分析结构如图6所示。

图6 层次分析结构Fig.6 Hierachieal stucture

按照发电效益重要度最高，机组利用效率、投资次之，弃水最次的重要度，构造装机容量原始矩阵见表6。

表6 原始矩阵Tab.6 Original matrix

不同方案的权重表如表7所列。

表7 不同方案的权重Tab.7 Weights of differeut schemes

其中，不同方案对发电效益、机组利用效率、弃水和投资的原始权重矩阵分别如表8～11所列。

表8 不同方案下发电效益的权重矩阵Tab.8 Weight matrix of power generation benefit under different schemes

表9 不同方案下机组利用效率的权重矩阵Tab.9 Weight matrix of unit utilization efficiency under different schemes

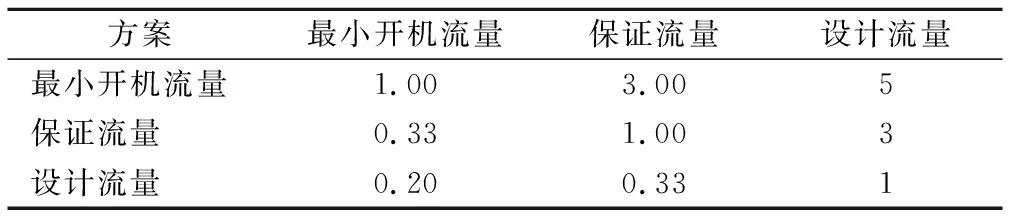
表10 不同方案下弃水的权重矩阵Tab.10 Weight matrix of abandoned water under different schemes

表11 不同方案下投资的权重矩阵Tab.11 Weight matrix of investment under different schemes

上述权重矩阵表的CR分别为：0.012，0.003 6，0.028，0.037，0.001 5，均小于0.1，满足一致性条件。

利用本文构建的层次分析法，最小开机流量、保证流量、设计流量3种方案的得分分别为0.42，0.27，0.31。

经过计算，按照发电效益>机组利用效率>投资>弃水重要度进行计算，可知，以生态流量作为最小开机流量确定的装机方案(1 200 kW)为最优方案。这主要是由于该方案可以充分利用4～9月的大流量，虽然机组利用效率较低，但是发电效益较大，弃水较少，符合实际情况。

若按照机组利用效率>发电效益>投资>弃水的重要度重新进行计算，最小开机流量、保证流量、设计流量3种方案的得分分别为0.36，0.37，0.27。

按照该重要度进行重新计算可知，其最优方案为以生态流量作为保证流量(即1 000 kW)的方案。该方案发电效益虽然有所减少，但是其对10月至次年3月的小流量利用较为充分，可以在满足机组利用效率的同时，提高发电效益，减少弃水。

5 结 论

随着绿色小水电建设工作的不断推进，水电站需要通过生态机组进行生态流量泄放，合理确定生态电站机组的装机容量成为关键。本文结合河流生态流量计算方法，构建了河流生态电站装机的确定模型，为水电站绿色改造中装机容量的论证决策提供必要的理论指导。 本文的主要研究成果如下：

(1) 分析了生态流量与装机容量确定的关系，明确了不同确定方法的适用性。

(2) 根据决策者的决策目标，选择发电效益、机组利用效率、弃水和投资4个部分为目标层，构建了生态电站装机方案的层次分析模型，该模型可以较好地解决生态流量装机方案确定的问题。