基于锚形谐振腔的等离子体波导特性研究
2023-03-06陈致远董兴法孙好
陈致远,董兴法,孙好
(苏州科技大学 电子与信息工程学院, 苏州 215009)
0 引言
表面等离子体激元(Surface Plasmon Polaritons,SPPs)是一种沿着金属和电介质界面传播的电磁波。SPPs具有将电磁波能量约束在半个波长区域的性质[1],可以突破传统光学中的衍射极限,被广泛应用于亚波长光学器件设计[2-3]。为激发SPPs,波导一般设计为介质-金属-介质(Insulator-Metal-Insulator, IMI)或金属-介质-金属(Metal-Insulator-Metal,MIM)结构。IMI波导损耗较低,但约束光传播的能力较弱。与之对应的,MIM结构具有较宽的频谱范围,在亚波长支持高群速模式,而且可实现长距离传播中精确的光调控[4],被广泛应用于纳米量级先进光学器件的设计,例如纳米级相干光源中的纳米腔[5]、矢量全息的双原子超表面[6]、T型带支节分束器[7]、定向耦合器[8]与红外窄谱增强传感器[9]等。
滤波器中的谐振腔具有波长选择性,利用SPPs与谐振腔耦合共振可以实现光的波长调控[10]。近年来,很多学者通过设计谐振器结构,制作了各种高性能滤波器,例如L形谐振腔滤波器[11]、方形凹环结构谐振器[12]与拱型谐振腔滤波器[13]等。
本文设计了一种基于锚形谐振腔的MIM波导滤波器,对该结构进行仿真,分析其传输特性。仿真结果表明,随着弧形结构角度θ、矩形结构高度H和弧形结构半径R的变化,共振波长处的滤波效果变化非常明显,且能够通过调整参数拟合数据得到对应关系精确控制滤波效果。若在锚形谐振腔内充入不同介质,由于SPPs对谐振腔内介质折射率敏感,可用于设计折射率传感器。
1 原理与数据仿真
1.1 模型建立与理论分析
本文设计的锚形谐振腔MIM结构滤波器示意图如图1,此滤波器由轴对称的弧形结构和垂直于波导的矩形结构组成,金属层为金属银。为使得谐振腔内只存在TM模式[13],将波导宽度和谐振腔宽度(包括弧形结构和矩形结构)固定为d=50 nm[14],直波导与锚形谐振腔的耦合距离固定为ω=10 nm。矩形结构高度为H,弧形结构半径为R,与波导垂线夹角为θ。波导和谐振腔(假定填充空气)介电常数εwaveguide=εcavity=1,金属银的介电常数采用Drude模型[15]计算
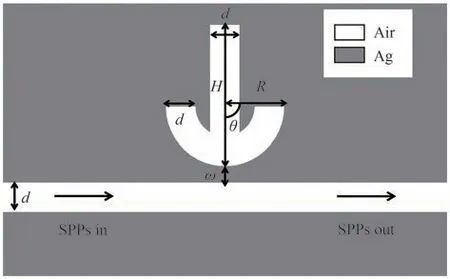
图1 锚形谐振腔MIM结构滤波器示意图Fig.1 Schematic diagram of anchor resonator MIM structure filter
式中,ε∞为无穷频率处的介电常数,ωp为等离子体共振频率,γ为电子碰撞的阻尼频率,ω为真空中入射光频率。计算时ε∞=3.7,ωp=1.38×1016Hz,γ=2.37×1013Hz。
波导左端为光入射端口,光功率为Pin,右端为光出射端口,光功率为Pout。使用透射系数T=Pin/Pout,评价光进入波导后的传输特性。在波导结构中,横向磁场传播模式的电磁场方程为[16]
式中,κ和d为波导传播的电磁波波矢和波导宽度。本文设计的波导由同一种金属组成,则p=q,αc=αs。p=εair/εAg,αc=[k02(εair-εAg)+κ]1/2。自由空间电磁波波矢k0=2π/λ0。计算得到波矢κ后,计算波导有效折射率neff=[εAg+(κ/k0)2]1/2,波导中传播的SPPs波长为λSPPs=λ0/Re(neff)。
2.2 仿真设置及结果
使用COMSOL Multiphysics仿真时设置上下表面为完美匹配吸收层以减少边界反射的影响。网格剖分时使用物理场控制网格,选择极细化以保证网格最大为波长的1/5。研究时需要在一个较宽的波长域进行遍历,精度和计算量的平衡显得尤为重要。经过反复测试,波长域定为400 nm~1 800 nm,遍历步长为5 nm时得到较为清晰的传输特性曲线。
引入品质因数Q的概念来评价滤波器的优劣,品质因数Q=λr/ΔFWHM[12]。其中,ΔFWHM为传输频谱的半峰全宽。当H=300 nm,θ=75°时锚形谐振腔滤波器传输特性如图2(a)。此结构参数下,波导存在4种共振模式如表1。

表1 当H=300 nm,θ=75°时,波导存在的4种共振模式Table 1 Four resonance modes of the waveguide when H=300 nm,θ=75°
图2(b)是相同尺度下的水平放置矩形谐振腔和L形谐振腔透射谱线。对比图2(a)可以发现锚形滤波器谐振波长处的透射率更低,半峰全宽更窄,品质因数更高,滤波效果更好。为进一步研究锚形谐振腔内的共振模式,计算4种模式下SPPs波在波导中的电场分布如图3。当SPPs耦合到锚形谐振腔,在谐振腔内形成稳定的驻波需要满足共振条件
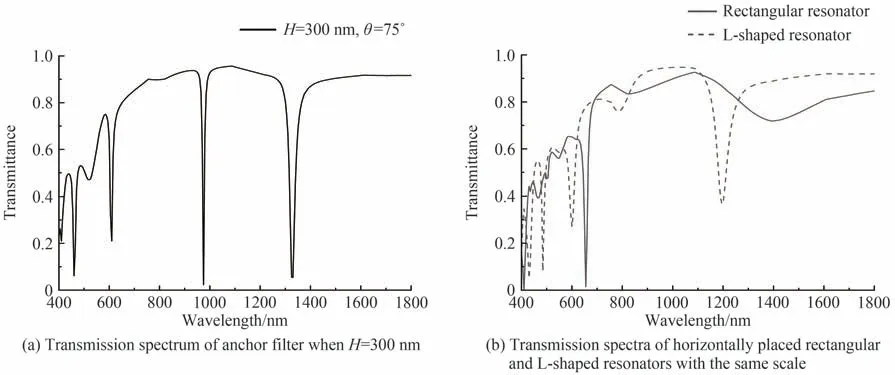
图2 不同谐振腔的滤波器透射谱线Fig.2 Transmission spectrum of filters with different resonators
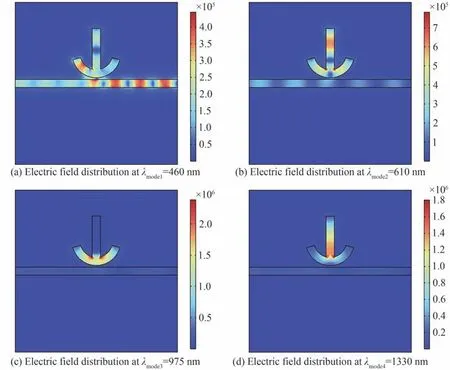
图3 各波长下的电场分布情况Fig.3 Electric field distribution at each wavelength
式中,φr为锚形谐振腔右侧面和上面的光束反射的反射相位;m为在锚形谐振腔形成驻波的波腹数;βm为腔内形成的m阶共振模式对应的SPPs的传播常数。在模式1中m没有正整数解,可见模式1中并没有在锚形谐振腔内形成稳定的驻波,SPPs与锚形谐振腔耦合后依然保持电场强度周期性变化,出现透射谱低谷是因为出射端口恰好位于电场强度谷值。模式2,3,4均满足共振条件,但电场分布不同。模式2中电场集中在弧形结构和矩形结构中,模式3中电场集中在弧形结构内,模式4中电场集中在矩形结构内。对比拱形谐振腔[13],本文结构在保证滤波效果的同时易于优化滤波器特征参数并且没有增加制造工艺难度。
2 结构参数影响分析
2.1 结构参数θ对传输特性的影响
为探究结构参数对波导传输特性的影响,进一步优化滤波结构,对结构参数θ进行分析,这里引入共振条件方程来解释谱线移动,共振条件为[17]
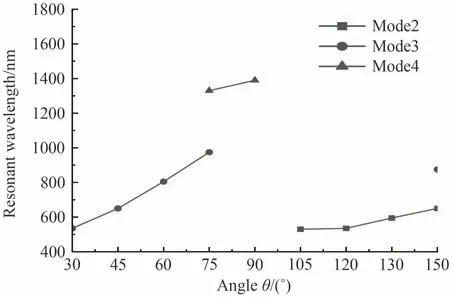
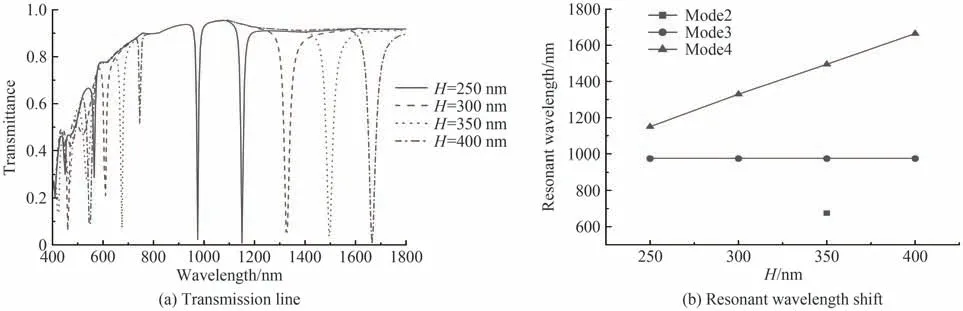
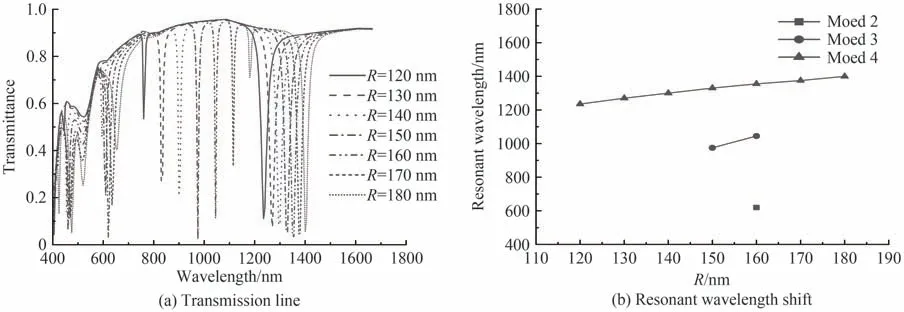
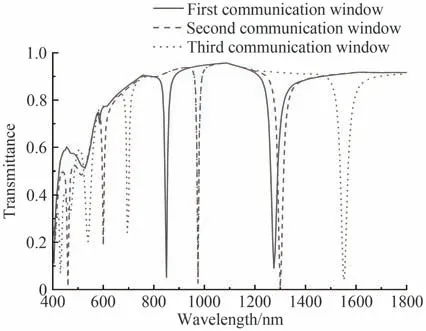
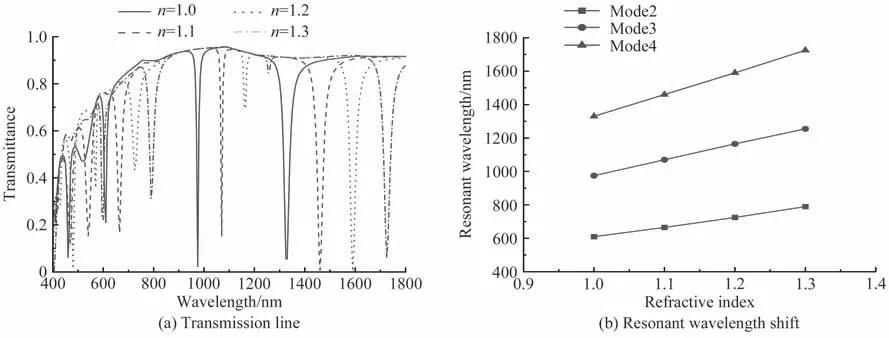
式中,Leff是锚形谐振腔的有效长度,λr是谐振腔的共振波长,N表示为模式数,neff是锚形谐振腔的有效折射率。当H=300 nm,R=150 nm时,角度θ对透射谱线的影响如图4。根据电场分布,模式1不属于滤波模式,模式2、3、4随夹角θ的增大,透射光谱发生红移并且透射低谷透射率出现变化。本文将透射低谷透射率大于0.1,滤波器明显失去滤波效果的情况排除,绘制了共振波长随夹角θ变化关系如图5。使用模式2设计滤波器时,夹角θ应该控制在105°~150°之间,拟合结果为λrmode2=2.8θ+220.5;使用模式3时,夹角θ应该控制在30°~75°之间,拟合结果为λrmode3=9.83θ+225;使用模式4时,夹角θ应该控制在75°~90°之间,拟合结果为λrmode4=4θ+1 030。拟合结果中函数斜率kmode2 图4 当H=300 nm,R=150 nm时θ变化时的透射谱线Fig.4 Transmission line with changing θ when H=300 nm and R=150 nm 图5 角度变化时共振波长变化谱线Fig.5 Spectrum of resonance wavelength with changing θ 在θ=75°,R=150 nm的情况下,研究结构参数H对传输特性的影响,结果如图6所示。由于模式2中强电场分布在弧形结构和矩形结构中,模式4中强电场大部分分布在矩形结构内,这两种模式随着H的增大,Leff随之增大,对应的共振波长λr发生红移。使用模式2设计滤波器时,只有当H=350 nm时满足滤波要求。模式3中强电场几乎全部分布在弧形结构内,H的变化不影响Leff,λmode3的偏移仅与θ有关。当θ=75°,R=150 nm时,共振波长λmode3始终为975 nm。模式4中拟合结果为λrmode4=3.42H+298.5,可以借此设计共振波长为675 nm、975 nm和1 150 nm~1 665 nm的窄带带阻滤波器。 图6 当θ=75°,R=150 nm,H变化时的透射谱线和共振波长偏移Fig.6 Transmission line and resonance wavelength shift with changing H when θ=75°,R=150 nm 在θ=75°,H=150 nm的情况下,探究结构参数R对传输特性的影响,结果如图7(a)所示。发现随着R从120 nm变化至180 nm,各模式均出现不同程度的谱线红移,其中模式3中红移现象最明显,与电场分布的分析结果一致。剔除明显不满足滤波要求的情况得到图7(b)。可以发现在模式2中,只有R=160 nm可以得到共振波长为620 nm的带阻滤波器。在模式3中,当R=150 nm~160 nm时,拟合结果为λrmode3=7R−75;在模式4中,当R=120 nm~180 nm,拟合结果为λrmode4=2.71R+916.4。根据上述拟合结果,可以设计波长为620 nm(模式2)、975~1 045 nm(模式3)、1 235~1 400 nm(模式4)的窄带带阻滤波器。 图7 当θ=75°,H=150 nm,R变化时的透射谱线和共振波长偏移Fig.7 Transmission line and resonance wavelength shift with changing R when θ=75°, H=150 nm 本节谈论了特定情况下的结构参数变化导致的传输曲线偏移,阐述了导致谱线红移的因素。综合考虑结构参数θ、H、R,利用拟合结果,可以设计特定波长的高性能窄带带阻滤波器。 将基于锚形谐振腔结构特性设计通信波长下的窄带带阻滤波器,以多模光纤的三个窗口为例进行设计。第一窗口使用模式3进行滤波,由图5得到当θ1=64°,H1=300 nm,R1=150 nm时满足要求。第二窗口和第三窗口使用模式4进行滤波,由图6(b)得到当θ2=75°,H2=293 nm,R2=150 nm和θ3=75°,H3=366 nm,R3=150 nm时达到对应的滤波效果,仿真结果如图8。仿真证明拟合公式精确描述了共振波长λr变化规律如表2。设计的三种通信窗口滤波器性能优越,与方形凹环结构MIM滤波器[9]相比(ΔFWHMmin=60 nm,Qmax=17.07)性能有明显提升,并且对一种窗口滤波时不会影响其他两种窗口的正常传输,实现了光通信中的通信窗口选择调控。 图8 通信窗口下带阻滤波效果Fig.8 Effect diagram of band stop filtering under communication window 表2 通信窗口下的窄带带阻滤波器性能参数Table2 Performance parameters of narrowband bandstop filter in communication window 研究共振波长λr对锚形谐振腔中介质折射率n的敏感特性,仿真得到不同折射率下透射光谱如图9(a)。图9(a)中发现随着介质折射率n增大,各模式共振波长均发生红移且透射波谷发生改变。模式4下共振波谷透射率T始终小于0.1且共振波长红移现象最为明显。传感器灵敏度是衡量传感效果的依据,灵敏度S=Δλr/Δn,其中Δλr为共振波长变化量,Δn为折射率变化量。9(b)中数据拟合得到=600 nm∙RIU−1,λrmode2=600n+7.5=933.3 nm∙RIU−1,λrmode3=935n+41=1 316.7 nm∙RIU−1,λrmode4=1 315n+14。MIM波导中的SPPs耦合对锚形谐振腔介质折射率敏感,可使用该特性制作传感设备。与L形谐振腔的MIM波导结构(Smax=1 166.7 nm∙RIU−1)相比,灵敏度有提升,更适合用于设计介质折射率传感器。 图9 锚形谐振腔内充入不同折射率n的介质Fig.9 Medium with different refractive index n filled in the anchor resonator 设计了一种基于MIM波导结构的锚形谐振腔滤波器,仿真分析表明,锚形谐振腔的结构参数θ、H和R会影响其滤波效果,实现了特定波长(通信窗口)下的窄带带阻滤波。在锚形谐振腔内充入不同折射率的介质,折射率增大引起了透射光谱红移,可为利用锚形谐振腔设计简单结构的介质折射率传感器提供理论依据。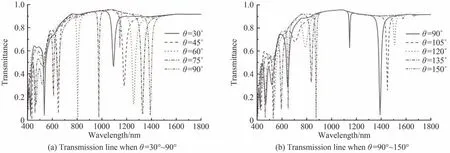
2.2 结构参数H对传输特性的影响
2.3 结构参数R对传输特性的影响
3 锚形谐振腔的应用
3.1 通信窗口下的窄带带阻设计

3.2 折射率传感特性
4 结论
