面向紧急避撞兼顾效率与舒适的变道轨迹规划方法研究

李洪硌，庞 海，夏红阳，黄永现，曾祥坤，徐 伟

（广东技术师范大学 汽车与交通工程学院，广东 广州 510665）

0 前言

轨迹规划在智能驾驶的决策过程中扮演着至关重要的角色，因此在国内外的科研领域备受重视.如何有效地规划车辆的路径，以确保它们在避开障碍物的同时平稳、舒适和安全地行驶，成为当前智能驾驶领域的研究热点[1].

针对局部路径的轨迹规划方法多种多样，各具特色.目前常见的轨迹规划方法包括基于侧向加速度的轨迹规划方法[2]、基于网络搜索的算法[3]、基于采样的规划方法[4]、人工势场算法[5-6].基于网络搜索的轨迹规划方法在进行较大面积区域轨迹规划时存在计算量过大的问题.基于采样的路径规划方法由于随机采样的原因存在计算量较大且规划出的轨迹不够平滑等问题.而人工势场轨迹规划方法在求解过程中容易出现局部最优解而造成死锁现象.

基于正反梯形侧向加速度的变道轨迹规划方法是根据变道时间要求，利用期望的侧向加速度便可以实现轨迹的规划，且期望的侧向加速度和侧向加速度率可结合车辆的动力学特性来确定，这使得该方法比较灵活，从而得到了广泛的应用.此外，该方法还可以通过对变道时间进行优化使得规划的轨迹曲线不受限于变道终点位置的局限，这也为实现不同行驶车速工况下的实时变道轨迹规划提供了可能.Li H L 等人[2]采用了基于侧向加速度的方法来研究直线变道情况下的变道轨迹规划.他们通过建立多目标函数，考虑了侧向加速度、横摆角速度、变道时间和变道距离等指标，以优化得到最佳的变道轨迹曲线.Guo L[7]等基于该方法进行了车辆在弯道进行变道的轨迹规划研究，并考虑了变道过程中的纵向和侧向运动学的耦合和弯道的内外侧道路不同曲率半径的特点，使得规划出的轨迹能较好的反映实际情况.

本研究在充分考虑本车不同行驶车速下进行变道操作的实际工况，基于正反梯形侧向加速度方法提出了一种兼顾安全性与舒适性并能适应不同行驶车速的变道轨迹规划方法.通过对多目标函数的优化求解得到侧向加速度和侧向加速度率的最优解，为实现基于该方法的变道轨迹的最优规划提供了新的解决方案.

1 正反梯形侧向加速度方法及目标函数建立

1.1 正反梯形侧向加速度方法

正反梯形侧向加速度方法是从变道车辆的侧向加速度出发，假设车辆在直线道路上变道操作过程中车辆侧向加速度的形状由一正一反两个大小相等的梯形组成，如图 1 所示，再通过对侧向加速度的两次积分得到变道轨迹曲线.对应期望的侧向加速度和侧向加速度率的数学表达式如式(1)和(2)所示[8-9].

式(2)中，a为侧向加速度，amax为最大侧向加速度；J为侧向加速度率，Jmax为最大侧向加速度率.

由此可以求得：

式中，dw为变道过程中的侧向位移，本文假定为车道宽，取3.5m.

由以上(3)(4)可以推出，侧向加速度值与侧向加速度率均可由时间t1、t2两个变量组成的表达式来表示，即：

故只需将变道过程中的侧向加速度与侧向加速度率进行约束，即可将轨迹规划问题转化为在满足侧向加速度和侧向加速度率最大值约束的条件下，针对相同的变道侧向移动距离dw=3.5m，求整个变道时间最短的数学非线性规划问题.

1.2 目标函数的建立及优化

衡量变道过程优劣的指标为变道过程中反映行驶安全性与乘坐舒适性的侧向加速度、反映方向盘转角变化率大小的侧向加速度率、反映车辆行驶稳定性的横摆角速度以及表征变道迅速性的变道时间和表征变道过程安全性的变道距离.综合考虑上述变道指标，建立变道过程的多目标函数.表达式如式（8）所示.

式中，ωi,i=1,2,3,4,5 分别代表各分项的权重系数，其取值可根据不同换道需求进行分配；aymax表示换道过程中的最大侧向加速度；Jmax表示换道过程中最大侧向加速度率；ωrmax表示换道过程中的最大横摆角速度；tc表示换道过程中的换道时间；latx表示换道过程中的行驶距离.

根据线性二自由度车辆模型，在线性区内汽车的侧向加速度和横摆角速度对转向盘转角的增益与车速的关系如下：

式中，δ表示前 轮转角,rad；νx表示车 速,km/h；m表示车辆质量,kg；L表示车辆轴距,m；lf表示质心至前轴距离,m；lr表示质心至后轴距离,m；Cr表示后轮侧偏刚度,N/rad；Cf表示前轮侧偏刚度,N/rad。

再根据公式(6)，可以得到最大横摆角速度ωrmax的表达式：

且变道时间可以表示为：

变道距离可以表示为：

则由公式（6），（11），（12）和（13），可以将式（8）所示的目标函数转化为：

式中，aymax-为aymax(m/s2)的左边 界；aymax+为aymax(m/s2)的右边界.此外，优化变量t1、t2还需要同时满足不小于 0 的下限条件.

1.3 目标函数的约束条件设定

变道过于激烈会使车辆侧向加速度过大，从而导致侧翻[10-11].为保证车辆在变道过程中的安全性，在轨迹规划时必须对最大侧向加速度aymax进行约束，如图2 所示.

（1）车辆行驶过程中侧向加速度只需达到0.8 倍的静态侧向加速度阈值就会侧翻，参考轿车准静态侧翻的平均值为1.41g[12]，则平均动态侧翻阈值aymax为1.128g(g=9.8m/s2) 故将此值作为紧急情况下的最大侧向加速度许可值.

（2）已有研究表明，在变道过程中，侧向最大加速度是影响乘坐舒适性的关键因素[13].在其研究中招募了不同性别以及不同晕车易感性的乘客进行实验并收集调查数据.数据结果表明，乘客评价没有不适时的平均最大侧向加速度为0.2g，约等于1.96m/s2.故当变道情形非紧急时，所规划变道正反梯形侧向加速度应小于等于1.96 m/s2.

（3）车辆在变道过程中主要关注最大侧向加速度的值（如图3 所示），在以舒适性为目的规划变道路径时，从理论上来说侧向加速度可以尽可能的小，以保持更加舒适的乘坐体验.但过小的侧向加速度会导致车辆变道效率变低，而车辆的变道效率也是影响整体交通效率重要指标，若车辆变更车道用时过长，则易导致整体交通拥堵，从而降低出行效率.变道持续时间的研究表明，在不拥堵的非高峰道路上最长变道时间不宜大于 9.7s，而当考虑变道效率时，变道时间t的最优解应小于等于平均变道时间 3.6s[14].

1.4 权重系数的取值范围

在式（14）中，ωi,i=1,2,3,4,5 分别代表各分项的权重系数，ω1表示换道过程中最大侧向加速度的权重系数，ω2表示换道过程中最大侧向加速度率的权重系数，ω3表示换道过程中的最大横摆角速度的权重系数，ω4表示换道过程中的换道时间的权重系数，ω5表示换道过程中的行驶距离的权重系数.为了能够通过控制单独一个变量从而调整变道轨迹偏向舒适或偏向效率.本文将变道过程中都视为变道乘坐舒适性的衡量指标的侧向加速度与横摆角速度权重等值为ωc，代表舒适性的权重系数，令ω1=ω3=ωc；将视为变道高效性的衡量指标的侧向加速度率、变道时间与变道行驶距离等值为ωe，代表效率性的权重系数，令ω2=ω4=ω5=ωe.再将代表舒适性的ωc与代表变道效率性的ωe的比值用字母ω表示，对应表达式如式(16)所示.

由式（16）可知，ωc越大，则ω值越大，变道轨迹越偏向舒适.反之，ωe越大，则ω值越小，变道轨迹越偏向效率，故ω值的大小可以表示变道轨迹的舒适倾向或者效率倾向，因此，通过改变ω值的大小即可改变变道轨迹的舒适倾向或者效率倾向.

1.5 通过曲线拟合实现权重系数自适应变化

在现实行车环境中，变道时遇到的情况往往是复杂多变的.在车速相对较慢且与前车车距相对较大时，所规划的变道轨迹可以偏向变道舒适性，使车辆以较小的侧向加速度以及横摆角速度进行变道.根据式（16），此时需要ω值偏大.而当车速相对较快且与前车车距相对较小时，所规划的变道轨迹可以偏向变道高效性，使车辆以更短的时间和变道距离进行变道，此时需要ω值偏小.故ω值的偏大或偏小取决于与前车的相对速度和与前车的相对距离，也就是与前车的碰撞发生紧急程度.目前车辆与前车发生碰撞的紧急程度主要由安全距离和安全相对速度判断[15].

TTC（Time-to-Collision）预碰撞时间是一个用于交通工程和机动车辆安全的概念，用来估算车辆之间在碰撞之前所需的时间[16].通常，TTC 是在自动驾驶系统和车辆安全系统中使用的一个重要参数，以确定车辆安全状态.TTC 的计算与自车、前车的行驶状态信息（自车行驶速度v0、加速度a0、前车行驶速度v1、加速度a1）有关[17].例如，在行驶过程中，车辆之间的距离过短、相对车速或加速度过大，都会导致Tttc值变小从而表 示碰撞 的风险变大.TTC 关 于v0、a0、v1、a1、drel的函数F(v0、a0、v1、a1、drel)为

其中，相对速度v0-v1设为vrel、相对加速度a0-a1设为arel,所以预碰撞时间与相对距离drel、相对加速度arel和相对速度vrel有关.

在计算预碰撞时间时，需要考虑前车与自车的运动状态.

当自车速和加速度均小于前车时，（vrel≤0,arel≤0），两车不会发生碰撞.

曲线拟合是一种数学和统计方法，用于从已知数据点集合中找到一个平滑的曲线并用函数表示，以近似地表示这些数据点的趋势或关系.由于此方法不依赖于被控对象的精确数学模型，在非线性系统控制中具有良好的鲁棒性等优势，在科学研究、工程领域和数据分析中都有广泛的应用.本文采用该方法对权重系数进行自适应调节，方法步骤如下.

（1）预先完成一系列不同TTC 下的测试，将不同TTC 与其对应满足舒适性或安全性（测试车辆与障碍车最小纵向距离为8m）的ω值数据记录.

本文取变道时TTC 范围0.4s-0.8s，并以0.05秒作为间隔进行测试，在平直道路下进行测试得到数据集如表1 所示.

表1 测试数据集

（2）将数据导入MATLAB 中进行函数拟合，得到曲线与关系函数.在三阶拟合后，所得函数曲线图像与数据集图像基本吻合，如图4.

得到的拟合函数为：

（3）建立控制器，将TTC 作为输入，通过控制器中拟合函数进行运算，输出ω值.再将ω值带入多目标函数中进行优化求解，即可得到理想正反梯形侧向加速度变道轨迹.

2 仿真验证

2.1 联合仿真平台搭建

为实现对所提方法的验证，本研究利用罗技G29 基于MATLAB 与Carsim 的联合搭建了联合仿真平台（如图5 所示）.将拟合的函数作为控制器，Carsim 输出的本车车速、相对距离、前车车速数值经运算得到TTC 后作为控制器输入，并得到ω值.将ω值代入多目标函数进行最优化求解即可得出最优正反梯形侧向加速度即可控制车辆进行变道试验.

2.2 车辆模型及变道场景搭建与测试

仿真试验所选用的车型是Carsim 自带车辆模型中的E-class,Sedan,变道时巡航速度为120km/h，障碍车辆车速为80km/h.路面为五车道高速路.变道情形为当本车与前车的预碰撞时间等于0.5 秒时与0.8 秒时分别执行变道操作.即在变道情况相对紧急与相对舒缓时进行仿真测试.记录变道时车辆的侧向加速度与变道时间，验证变道规划在紧急变道时的安全性与高效性，和在舒缓变道时的舒适性.

（1）TTC 为0.5s（变道情况相对紧急，需高效变道），将此信息输入至拟合函数，对应得到权重系数为ω=15.77.经仿真实验得到在此权重系数下变道的最大侧向加速度为3.25m/s2；变道时间为2.5s.

（2）TTC 为0.8s（变道情况相对舒缓，需舒适变道），将此信息输入至拟合函数，对应得到权重系数为ω=100.1.经仿真实验得到在此权重系数下变道的最大侧向加速度为1.03m/s2；变道时间为4.1s.

由以上仿真结果曲线图（图7 和图8）可以得出，在不同的预碰撞时间情况下，优化得到的变道轨迹不同.当TTC 数值较小，变道较为紧急时，规划出的变道轨迹侧重效率性，变道时间较小，而侧向加速度仍远远小于车辆可能发生侧滑失控的临界加速度（11.05m/s2）.故在紧急情况下既保证了变道的高效性，避免与前方障碍物发生碰撞，又保证了安全性，即变道过程中不会发生侧滑甚至侧翻.而当TTC 数值较大，即变道较为舒缓时，规划出的变道轨迹侧重舒适性，变道时的最大侧向加速度远远小于理论上认为舒适的加速度.即保证了充分的舒适度，虽变道时间有所增加，但仍远小于最长变道时间（9.7s）.

为进一步验证不同预碰撞时间下（对应不同碰撞紧急程度）的变道轨迹规划的效果，又在假定车辆保持某一确定车速行驶（以 100km/h 车速为例）的条件下，通过改变不同TTC 值进行仿真分析.仿真得到的不同权重系数下变道过程最大侧向加速度与变道时间的关系曲线如图11所示.可以看出，在TTC 较小时（即变道情况较为紧急时），变道时间较小，即此时所提方法规划的变道轨迹侧重变道迅速性.而当TTC 较大时（即变道情况较为舒缓时），所提方法规划的变道时间有所延长，而最大侧向加速度显著减小，即侧重乘坐舒适性.这也非常好的贴合了实际驾驶员的驾驶意图，为解放驾驶员实现智能驾驶提供了可能.

图1 正反梯形侧向加速度示意图

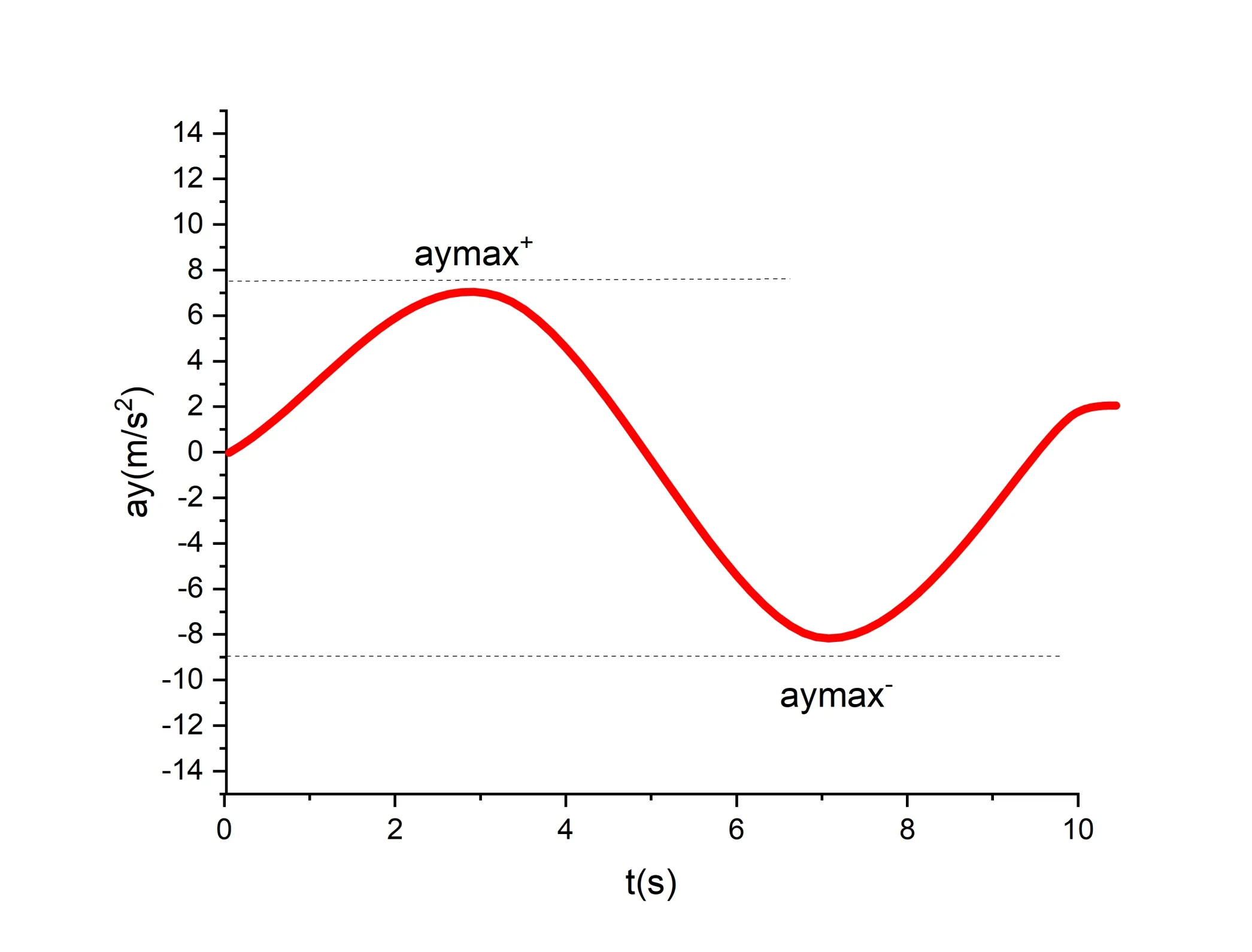
图2 侧向加速度上下边界约束示意图

图3 车辆变道时侧向加速度变化示意图

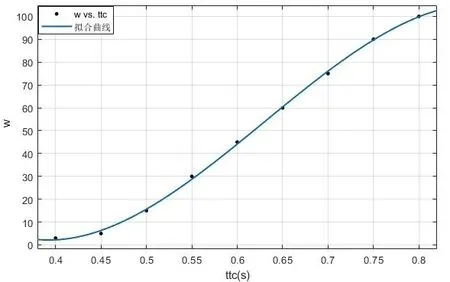
图4 拟合曲线

图5 MATLAB/Carsim 联合仿真平台

图6 仿真测试场景

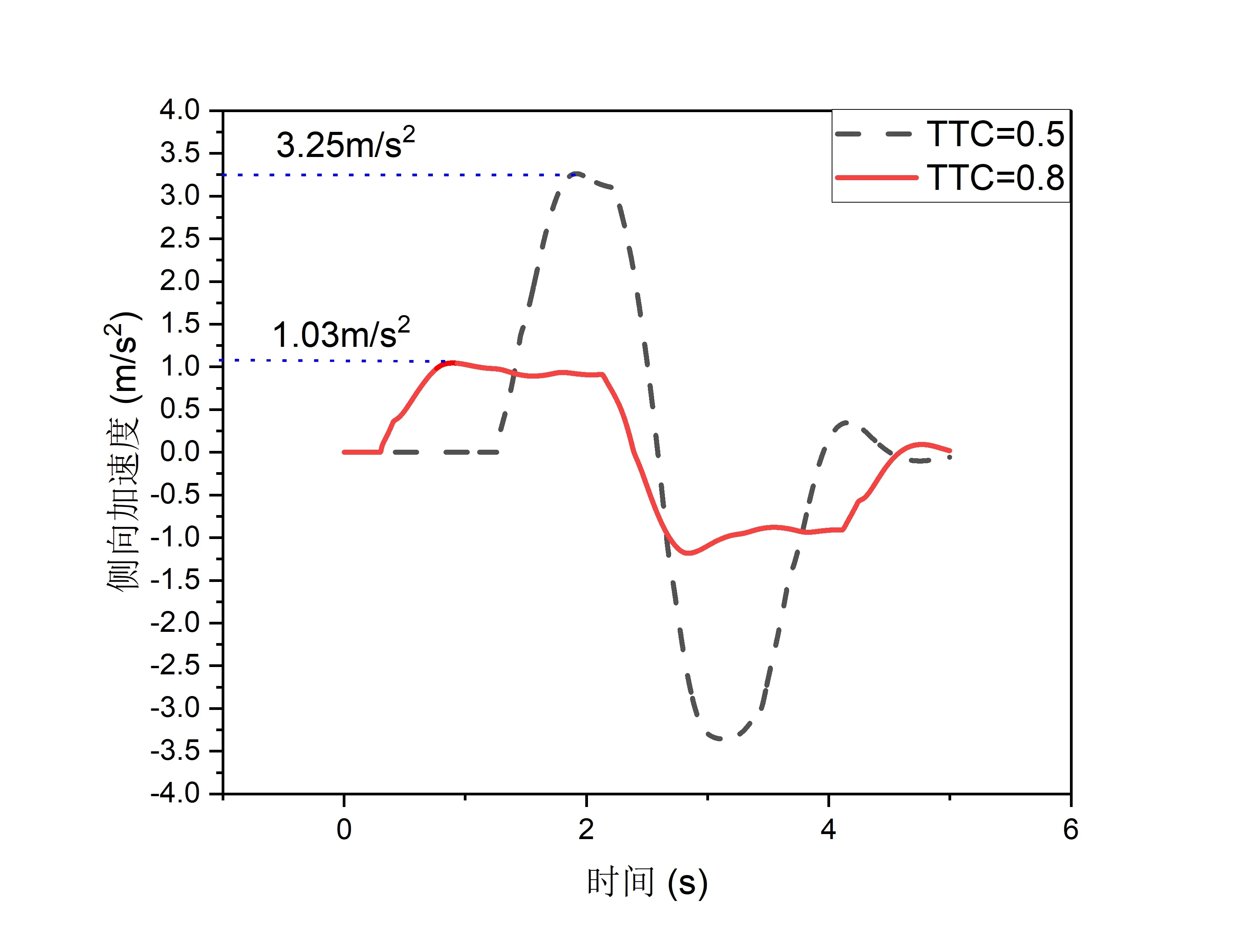
图7 侧向加速度曲线对比图

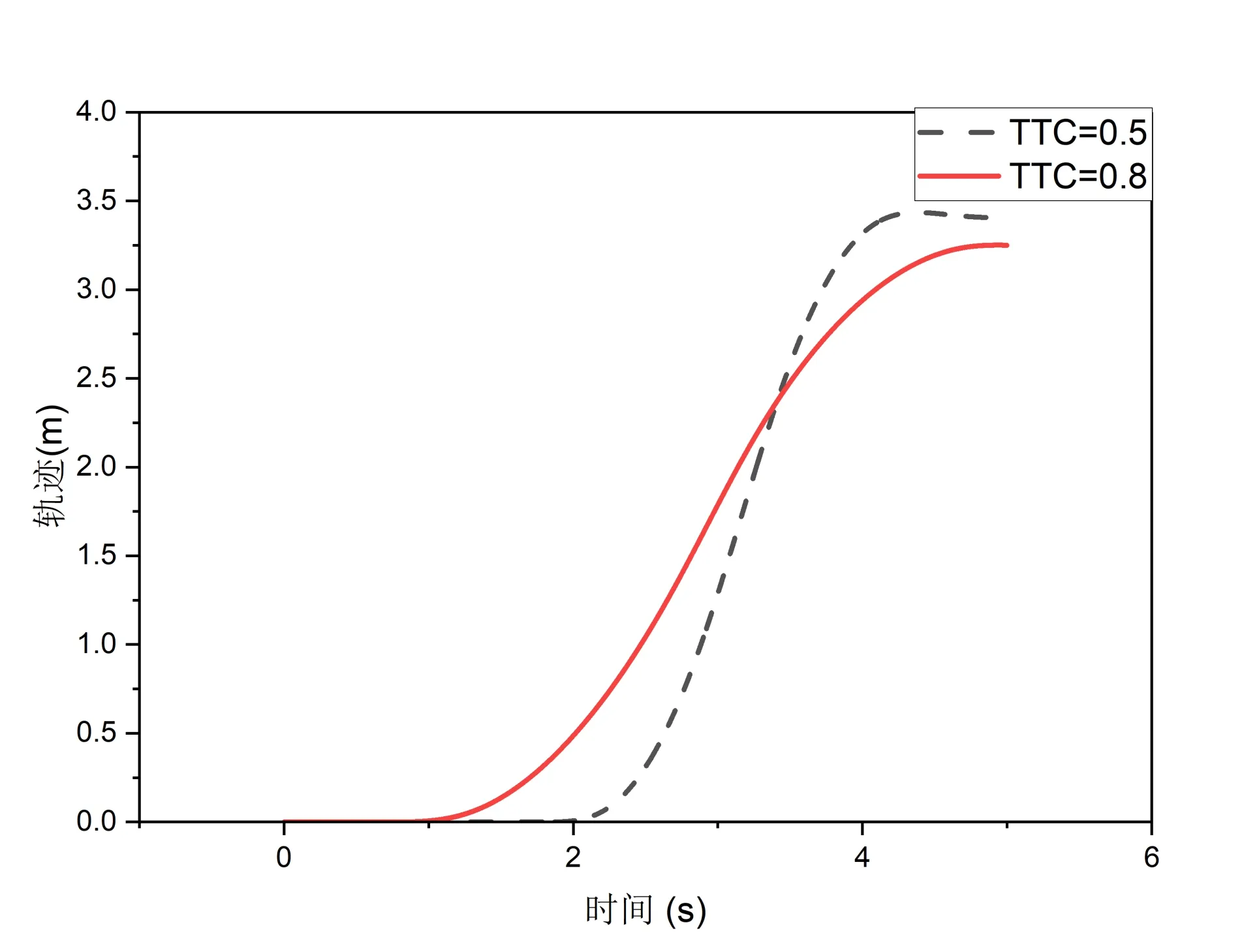
图8 变道轨迹曲线对比图

图9 ω=15.77 时变道效果图

图10 ω=100.1 时变道效果图

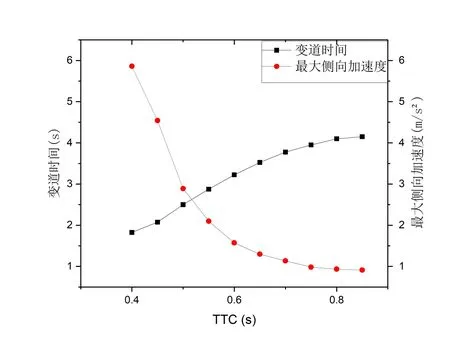
图11 不同预碰撞时间下的变道时间与最大侧向加速度关系图

2.3 曲线函数拟合方法通用性验证仿真测试

本文为实现自适应ω值所提出的基于函数曲线拟合方法具有广泛的适用性以及较强的通用性.在实际运用中，使用者可以在收集不同TTC 所对应的ω值数据集合时，根据实际车型、实际道路情况与预期变道效果自行调整及标定ω值，（例如，规定测试车与障碍车最小纵向距离不得小于12m），或可缩短测试TTC 最小间隔时间以提高曲线精度，得到符合自身要求的曲线，最终得到符合要求的函数图像.故该方法可以适用于不同的变道需求，并实现在不同需求下规划出最安全高效的变道轨迹.

在通用性验证仿真测试中，更改安全标定，将与前车最小纵向距离设置从前文测试时的8m扩大为12m，故可将最小TTC 扩大并更改ω值标定，其余条件不变，收集到测试数据集如表2所示.

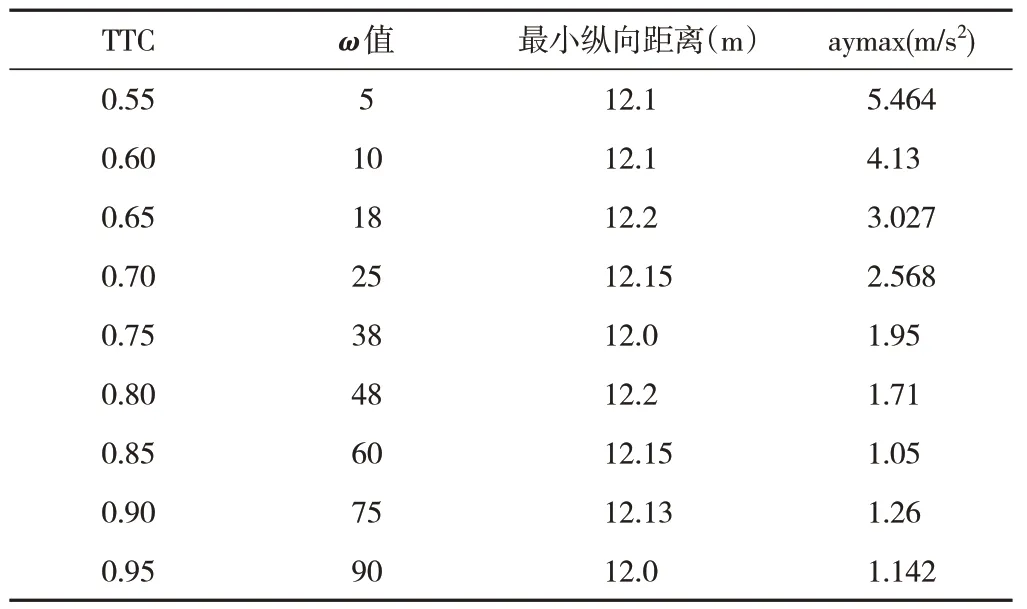
表2 测试数据集

将数据导入MATLAB 中使用cftool 工具进行函数拟合，得到曲线与关系函数.在3 阶拟合后，所得函数曲线图像与数据集图像基本吻合，如图12 所示.

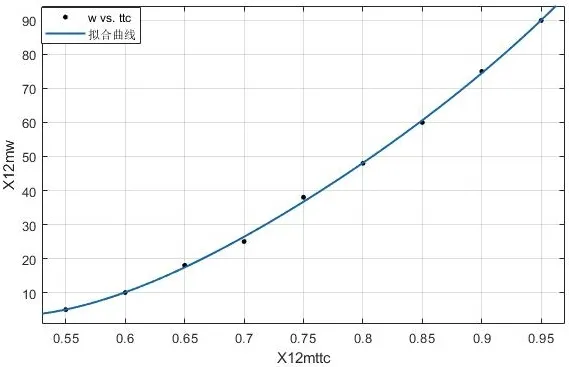
图12 更改标定后的拟合曲线

得到的拟合函数为：

为证明方法有效性，将以函数（20）作为控制函数的轨迹规划结果作为实验组，而以函数（19）作为控制函数的轨迹规划结果作为对照组进行测试对比.验证不同的标定下所规划出的变道轨迹和变道效果是否有显著区别，并观察试验组车辆与障碍车的最小纵向距离是否变化且满足要求（大于12m）.

测试情形均为试验车保持110km/h 与障碍车保持60km/h 在五车道高速公路上同向行驶，且在TTC=0.72s 时开始变道.

由图13 和图14 可以看出，不同的ω值标定下的控制函数在相同的TTC 下有着明显不同的与前车最小纵向距离和变道轨迹.实验组所规划的变道轨迹目标是使得变道过中与前车最小纵向距离约为12m，而测试结果得出与前车最小纵向距离为12.3m，极其接近目标距离，很好的适应了目标变道需求.与此同时测得最大侧向加速度为2.306m/s2，远远小于安全侧向加速度边界，并且保持了一定的舒适性.

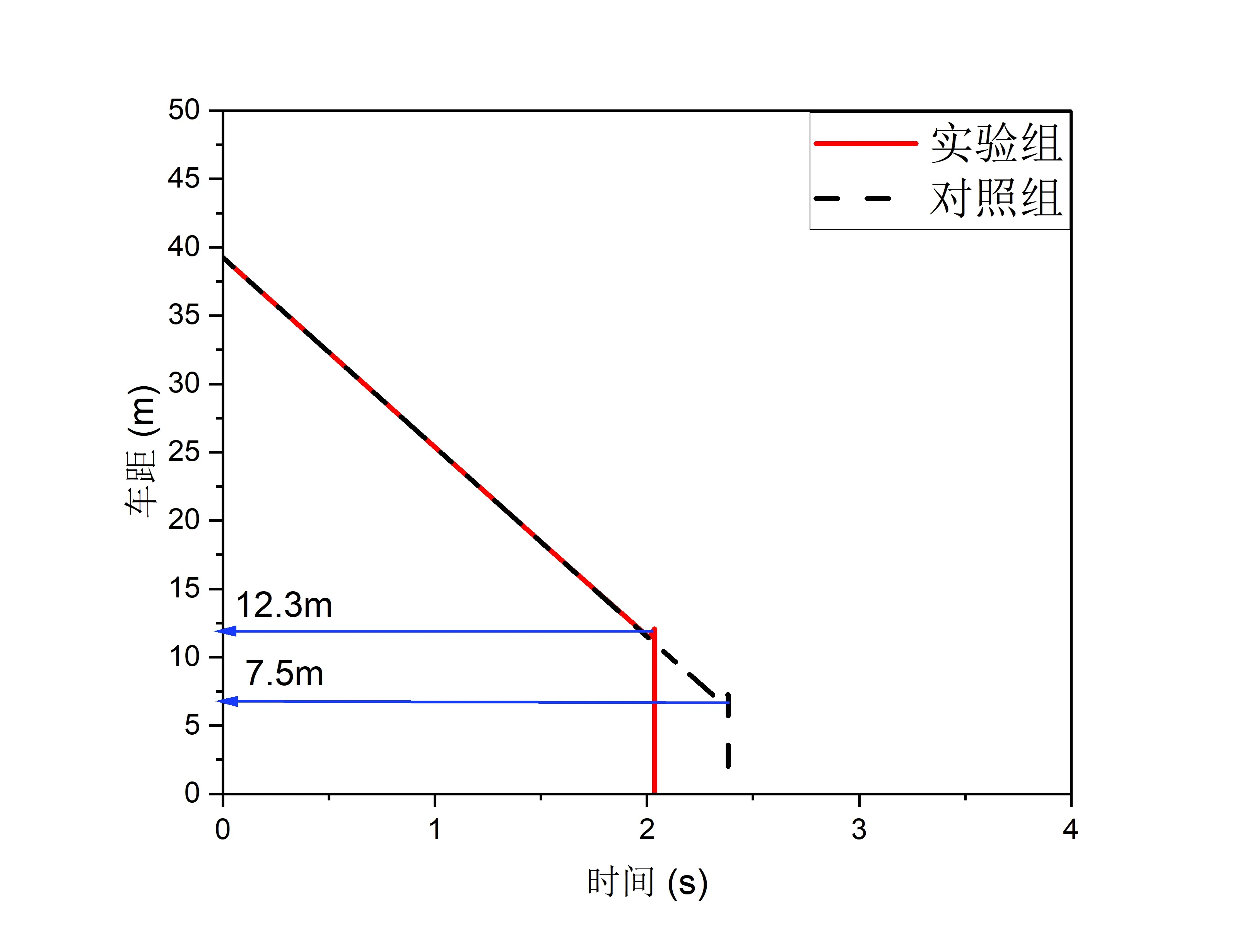
图13 对照组与实验组变道最小车距对比图

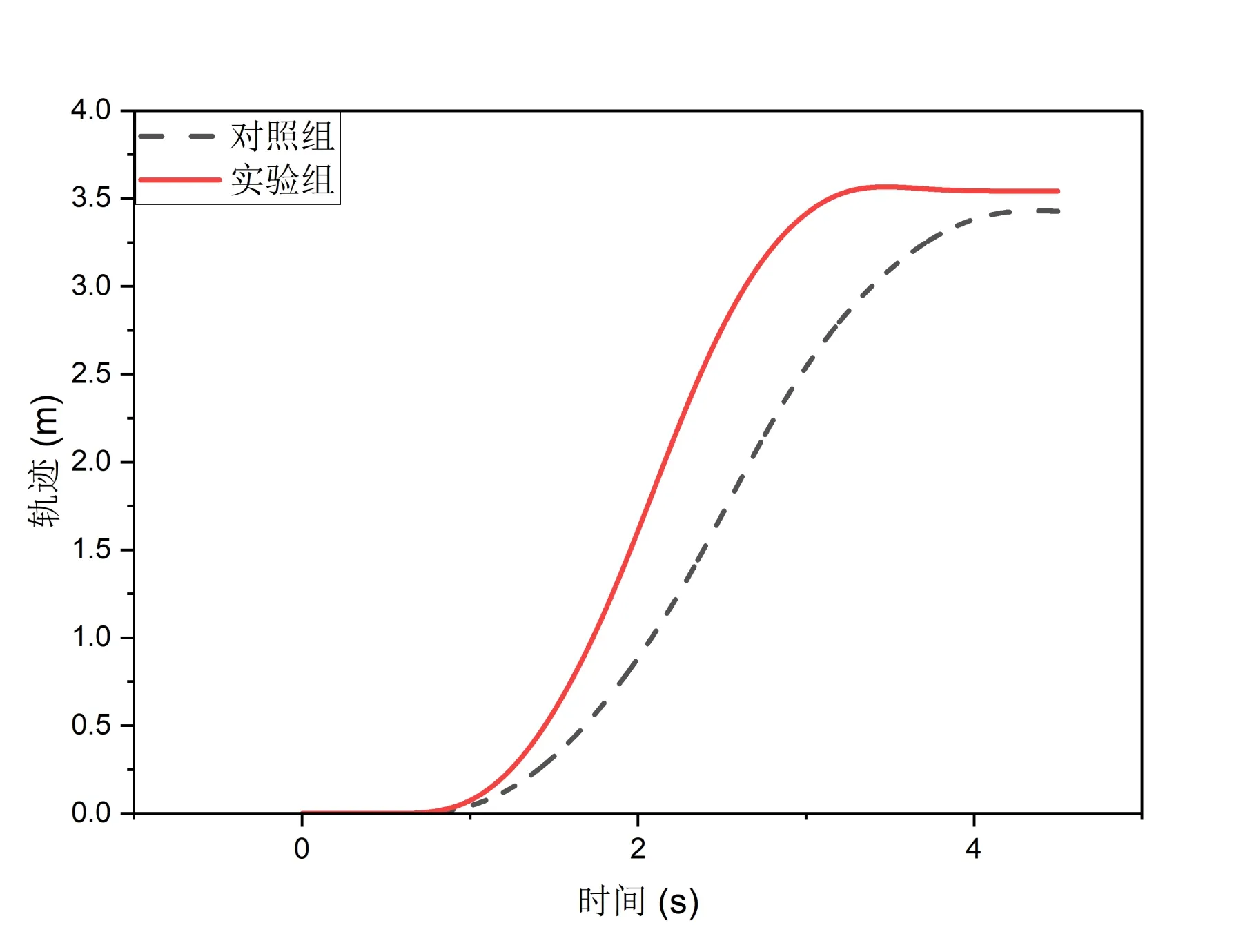
图14 不同ω 值标定控制函数在相同TTC 时间变道轨迹对比图

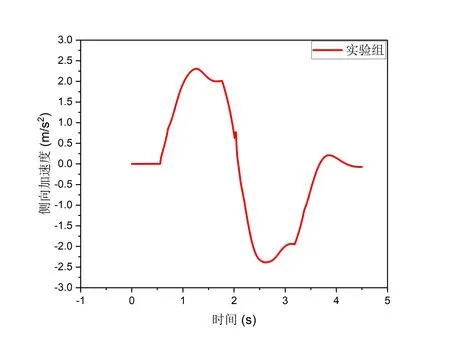
图15 实验组控制下侧向加速度图

综上仿真结果可得本文所提利用函数曲线拟合的变道轨迹规划控制方法能个性化的满足广泛的变道需求及目标，并在确定变道轨迹控制函数后能够做到自适应控制ω值以保证车辆的变道安全性、高效性以及舒适性.

3 总结

本研究针对紧急避撞工况提出了一种兼顾效率与舒适性的自适应轨迹规划方法.首先，基于正反梯形侧向加速度的轨迹规划方法，以影响变道舒适性的车辆侧向加速度、侧向加速度率、横摆角速度，以及影响变道效率的变道时间和变道距离作为目标建立多目标函数，并建立舒适度与效率的权重系数变量.然后，针对侧向加速度与变道时间界定边界，通过对多目标函数的优化求解、实验测试以及拟合函数，得出了一种可以个性化设定变道需求，同时在不同预碰撞时间的条件下得出自适应权重系数值以规划出优化变道轨迹的方法.最后，通过MATLAB/Carsim 联合仿真平台对所提方法进行了仿真验证.结果表明，所提方法在不同预碰撞时间条件测试下都能够规划出理想的变道轨迹.