集中载荷作用下双模量矩形截面梁的弹性解

李 政,肖 珍,吴 晓

(常德学院智能建筑学院,中国 常德 415000)

双模量材料结构已开始在工程实际中被广泛应用,例如纳米吸波材料石墨/环氧树脂复合材料就是典型的双模量材料,其拉伸区的弹性模量是压缩区的弹性模量的4倍。因此,研究双模量材料结构的文献逐渐增多。文献[1]采用蚁群算法求解了二维拉压不同模量反问题,文献[2]研究了基于敏度分析的拉压不同模量桁架问题的数值分析,文献[3]研究了不同拉压特性的厚壁球壳分析,文献[4]基于应力球张量法的不同模量陶瓷梁有限元分析,文献[5]研究了基于双模量理论的均布载荷下简支梁的解析解及数值分析,文献[6]给出了拉压弹性模量不同曲梁的弹性解,文献[7]采用弹性理论研究了拉压弹性模量不同矩形截面杆的弯曲,文献[8]研究了拉压弹性模量不等材料简支梁的线性振动问题。但是,文献[1-8]均没有研究集中载荷作用下双模量矩形截面简支梁的弯曲变形。本文借鉴文献[9]和[10]的半逆解方法研究了集中载荷作用下双模量矩形截面简支梁的弯曲变形,以完善双模量材料梁弹性计算理论,为工程计算设计提供理论依据。

1 弯曲应力表达式

以图1所示双模量矩形截面简支梁为例,研究其弯曲变形。

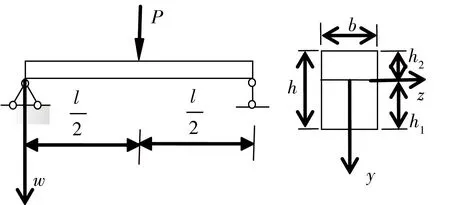
图1 集中载荷作用下简支梁

由弹性理论可知,梁的应力可用应力函数表示为

(1)

式中,φi为应力函数,i=1表示拉伸区,i=2表示压缩区。

由文献[7]可知双模量梁弯曲时,拉伸区、压缩区距离中性轴的高度分别为

(2)

式中,E1,E2分别为拉伸区、压伸区弹性模量。

对于图1所示简支梁忽略体力作用时,剪应力在梁上下表面均为零,且沿x方向无变化。参阅文献[9-10]并结合式(1)可令应力函数为

φi(x,y)=x(Aiy3+Biy2+Ciy)+Hiy3+Kiy2。

(3)

把式(3)代入式(1)中可得

σxi=x(6Aiy+2Bi)+6Hiy+2Ki,σyi=0,τxyi=-(3Aiy2+2Biy+Ci)。

(4)

图1所示简支梁应力边界条件为

x=0,y=0,σx1=σx2=0,

(5a)

y=h1,τxy1=0,

(5b)

y=-h2,τxy2=0。

(5c)

图1所示双模量简支梁中性层连续条件为

y=0,σx1=σx2=0,τxy1=τxy2。

(6)

利用式(1)及式(5a)可得

σx1=6H1y,σx2=6H2y,K1=K2=0。

(7)

由于图1所示简支梁在x=0处,梁截面弯矩为零,因此梁截面拉压弯曲应力也为零,由式(7)可知

H1=H2=0。

(8)

再利用式(4)和式(6)～(8)可知

B1=B2=0。

(9)

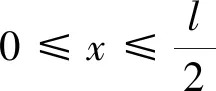
(10)

利用式(4)和(5b)可得

(11)

把式(4)和(11)代入式(10)可得

(3)1∶25 000水系沉积物测量较1∶50 000水系沉积物测量结果更佳。不仅对异常的反应更准确，而且更有利于指导下一步找矿。

(12)

把式(7)～(9)和式(12)代入式(4)中可得图1所示简支梁拉伸、压缩区应力表达式分别为

(13a)

(13b)

当E1=E2时,式(13)皆退化为材料力学给出的应力公式。

2 挠曲线表达式

由弹性理论可知图1所示双模量简支梁应力与应变关系为

(14a)

(14b)

(14c)

式中,ui为梁轴向位移,wi为梁弯曲挠度,μi为泊松比。

把式(13)代入式(14a)中可求得拉伸区、压缩区的轴向位移为

(15a)

(15b)

把式(13a)拉伸区应力分量代入式(14b)中可得拉伸区、压缩区的弯曲挠度为

(16a)

(16b)

把式(15a)和(16a)代入式(14c)中可得

(17)

把式(15b)和(16b)代入式(14c)中可得

(18)

由式(17)可以求得

(19a)

(19b)

(20a)

(20b)

图1所示双模量简支梁的边界条件为

x=0,y=0,u1=w1=0,

(21a)

y=0,w1=w2,

(21b)

(21c)

x=0,y=0,u2=w2=0。

(21d)

利用式(15)和(16)、式(19)和(21)可以得到图1所示简支梁拉伸区、压缩区的轴向位移挠度表达式及弯曲挠度表达式分别为

(22a)

(22b)

(22c)

(22d)

式(22)即为集中载荷作用下双模量简支矩形截面梁拉伸区、压缩区的轴向位移及弯曲挠度表达式。

3 讨论分析

本节讨论集中载荷作用下双模量简支矩形截面梁的弹性理论解和把集中载荷作用下双模量简支矩形截面梁作为各向同性材料梁材料力学解的误差。

材料力学方法给出了把图1所示集中载荷作用下双模量简支矩形截面梁作为各向同性材料梁弯曲应力公式为

(23)

材料力学方法给出了把图1所示集中载荷作用下双模量简支矩形截面梁作为各向同性材料梁的中性轴挠曲线表达式为

(24)

利用式(13)和(23)可以得到本文方法求得的任意梁截面最大弯曲应力公式与材料力学方法求得的任意梁截面最大弯曲应力公式的误差表达式为

(25a)

(25b)

(25c)

利用式(22)和(24)可以得到,当Ei=E1,Ei=E2时,本文方法得到的中性轴处弯曲挠度与材料力学方法得到的中性轴处弯曲挠度的误差表达式分别为

(26a)

(26b)

下面把式(25)和(26)计算的误差值均列在表1～5中以便讨论分析。具体计算数值可见表1～5。

表1 拉应力误差 δ1 单位:%

表2 压应力误差 δ2 单位:%

表3 剪应力误差 δ3 单位:%

表4 弯曲挠度误差 δ4( Ei=E1 ) 单位:%

表5 弯曲挠度误差 δ5 ( Ei = E2) 单位:%

由以上推导计算可知,式(22)给出了集中载荷作用下双模量简支矩形截面梁拉伸区、压缩区的轴向位移及弯曲挠度表达式,这说明双模量梁截面任意点的弯曲挠度都不相同,而材料力学方法仅能推导出集中载荷作用下双模量简支矩形截面梁的中性轴挠曲线表达式。

对表1～5进行分析可以知道:对于集中载荷作用下双模量简支矩形截面梁,当0.91.1时,双模量梁拉伸区、压缩区的弯曲应力与把双模量简支矩形截面梁作为各向同性材料梁的弯曲应力的误差皆大于5%。当0.6

4 结论

(1)本文方法给出了集中载荷作用下双模量简支矩形截面梁拉伸区、压缩区的轴向位移及弯曲挠度表达式,这说明双模量梁截面任意点的弯曲挠度都不相同。

(2)当0.9

(3)双模量简支矩形截面梁中性轴处弯曲挠度对n值变化很敏感,原则上建议计算双模量简支矩形截面梁中性轴处弯曲挠度应采用弹性理论。