Fe 掺杂对Ni-Mn-Ti 全d 族Heusler 合金马氏体相变和磁性能影响的研究*

金淼 白静† 徐佳鑫 姜鑫珺 章羽 刘新 赵骧 左良

1) (东北大学材料科学与工程学院,材料各向异性与织构教育部重点实验室,沈阳 110819)

2) (东北大学秦皇岛分校资源与材料学院,河北省电介质与电解质功能材料重点实验室,秦皇岛 066004)

Ni-Mn-Ti 基全d 族Heusler 合金因具有良好的力学性能和弹热效应而成为金属功能材料领域的研究热点,然而此类合金具有临界应力和滞后较大的问题限制了其实际应用.有研究学者发现Ni-Mn 基合金掺杂Fe 不仅可以降低相变滞后,还可以大幅提高合金力学性能.鉴于此,本文采用第一性原理计算系统地研究了Fe 掺杂对Ni50—xMn37.5Ti12.5Fex(x=3.125,6.25,9.375)全d 族Heusler 合金的相稳定性、马氏体相变和磁性能的影响.结果表明随着Fe 掺杂量的增多,奥氏体的晶格常数逐渐减小;相稳定性随着Fe 掺杂量的增加而逐渐降低,但在不同成分下,马氏体始终比奥氏体更稳定,表明合金可以发生马氏体相变.合金的奥氏体相为铁磁性,磁矩主要由Mn 原子提供,而马氏体相由于正常占位的Mn(MnMn)原子与占据Ti 位的富余Mn(MnTi)原子的磁矩反平行排列而表现为反铁磁性.Fe 取代Ni 使Ni50—xMn37.5Ti12.5Fex 合金系奥氏体和马氏体之间的能量差ΔE、电子浓度e/a 和电子密度n 都呈现减小趋势,表明合金的马氏体相变温度随着Fe 原子掺杂量的增多而下降.本文旨在为新型Ni-Mn-Ti-Fe 合金的成分设计和性能优化提供指导.

1 引言

Heusler 型形状记忆合金由于拥有种类众多、物理性能丰富和通过掺杂不同元素可以精细调节合金性能等优点而备受研究者的关注,成为近期凝聚态物理和材料学领域的研究热点[1].Ni-Mn-X基Heusler 合金是一类新型智能材料,兼具大磁致应变[2,3]、大输出应力[2]和高的响应频率[4],且伴随发生在马氏体相变和磁性转变点附近的可逆磁热效应[5-+],以及磁性转变点之上的弹热效应[8-+].这些优异的综合性能使其在制动器[11]、传感器[12]、能量收集装置[13]和固态制冷[7,14]等技术的应用方面具有潜在的优势.

传统的Ni-Mn-X(X=Ga,In,Sn,Sb 等)Heusler 合金具有高度有序的原子占位,其中主族元素X提供的p 层电子与过渡族元素Ni 和Mn提供的d 层电子形成共价键.尽管传统Heusler 合金有许多优点,但由于其特有的p-d 键合导致本征脆性大,极大地限制了该合金投放到实际应用中.中国科学院物理研究所刘恩克等[15]于2015 年开创性地提出了以Ni-Mn-Ti 为代表的全过渡族(又称“全d 族”)Heusler 合金,为Heusler 家族开拓了新的研究方向[16,17].与传统Heusler 合金母相高度有序的L21结构不同,Ni-Mn-Ti 合金的母相为部分无序的B2 结构.正是由于原子占位的部分无序性,使得该体系合金的奥氏体和马氏体均呈现反铁磁性,因此不能像传统Ni-Mn 基Heusler 合金那样在马氏体相变过程中产生磁-结构耦合转变,即不具备磁热效应.

为此,国内外的研究人员利用第四组元掺杂和改变合金制备工艺对其进行了优化.Wei 等[18]发现向Ni-Mn-Ti 合金中掺杂一定量的Co 元素可以使合金奥氏体母相从反铁磁态转变成铁磁态.并发现Ni35Co15Mn35Ti15合金在温度为253 K、强度为120 kOe 磁场的作用下产生2400×10—6的应变,在磁场变化量为50 kOe 的情况下Ni35Co15Mn35Ti15样品还测得了18 J·kg—1·K—1的磁熵变[19].Guan 等[20]在5 T 磁场的室温下发现了Ni36Co14Mn35Ti15非织构多晶合金的最大磁化强度变化和磁熵变化分别达到106 emu/g 和19.3 J·kg—1·K—1,铸态合金的最大抗压强度和塑性分别超过1220 MPa 和15%.Liu 等[21]发现Ni37Co9Fe4Mn35Ti15合金在3 T 的外加磁场下可以产生最大为8.4 J·kg—1·K—1的磁熵变,该合金还能够在400 MPa 的单轴应力下产生6.3 K 的绝热温变[10],在300 MPa 的应力下加载卸载循环上千次仍然没有断裂.Taubel 等[22]发现当Ni37Co13Mn34Ti16合金在2 T 的磁场变化下表现出38 J·kg—1·K—1的等温熵变,并且该成分合金处于253 K 的温度时,表现出—3.5 K 的最大绝热温变.Li 等[23]开发了一种价格低廉的(Ni50Mn35.5Ti14.5)99.8B0.2多晶高温形状记忆合金,该合金表现出完美的超弹性,在423—553 K 的宽温度范围内具有高达7.1%的完全可恢复应变,并且具有最大可恢复应变6.0%的双向形状记忆效应[2,24,25].

到目前为止,研究主要集中在掺杂Co 和B 元素[26,27],掺杂Co 可以激活Ni-Mn-Ti 合金的磁热效应,微合金化元素B 可以增强合金的弹热效应循环稳定性和提升其力学性能[28].而对Ni-Mn-Ti 合金掺杂Fe 的研究较少,而Fe 作为铁磁性元素掺杂进Ni-Mn-Ti 合金会对合金的马氏体相变、磁性能和力学性能产生重要影响.鉴于此,本文采用第一性原理计算的方法研究了不同含量的Fe 掺杂对Ni50—xMn37.5Ti12.5Fex合金马氏体相变、磁性能和电子结构的影响,旨在为新型Ni-Mn-Ti-Fe 合金的成分设计和性能优化提供指导.

2 计算方法

利用Vienna Ab-initio Simulation Package(VASP)软件包进行了基于密度泛函理论(DFT)下的第一性原理计算[29].离子与电子的相互作用用投影增强波(PAW)方法描述,交换关联势采用PBE-GGA 方法处理[30].涉及元素的电子构型为Ni-3d84s2,Mn-3d64s1,Ti-3d34s1和Fe-3d74s1.平面波基矢的截断能设为351 eV.布里渊区通过 Monkhorst-Pack 方法进行采样[31].奥氏体和马氏体的K 点网格分别为10×10×5 和7×7×11.在结构优化过程中,总能量和原子间力的收敛标准分别被设定为1 meV 和0.02 eV/Å,外压力在±3 kbar(1 bar=105Pa)之内.

计算所使用的Ni-Mn-Ti 合金具有部分无序的B2 结构奥氏体母相(A)和L10结构的非调制马氏体相(NM).为了保证在第一性原理计算时各相中掺杂的Fe 原子浓度相同,B2 奥氏体相和L10马氏体相均采用包含32 个原子的超胞进行计算.为便于描述,铁磁性和反铁磁性的奥氏体和马氏体分别命名为FA,AFA,FM 和AFM.

在Ni50—xMn37.5Ti12.5Fex(x=3.125,6.25,9.375)合金系中,形成能(Ef)[20]的计算用(1)式描述:

其中E0是化合物经过结构优化后的总能量,NNi,NMn,NTi和NFe分别是晶胞中Ni,Mn,Ti 和Fe原子的数目,ENi,EMn,ETi和EFe分别是一个Ni,Mn,Ti 和Fe 原子在其块状纯元素下单个原子的基态能量.

3 结果与讨论

3.1 相稳定性与晶格常数

为了准确描述Fe 的掺杂量对Ni50—xMn37.5Ti12.5Fex(x=3.125,6.25,9.375)合金系物理性能的影响情况,首先对Fe 原子在Ni50—xMn37.5Ti12.5Fex合金奥氏体相中的分布情况进行了研究,对聚集分布和离散分布这两种Fe 原子的分布方式进行计算讨论,见图1(b1)和图1(b2)所示.这两种分布情况下的形成能分别为—95.37 meV/atom 和—94.93 meV/atom,表明Fe 原子在Ni50—xMn37.5Ti12.5Fex(x=3.125,6.25,9.375)合金系中更倾向于聚集分布.

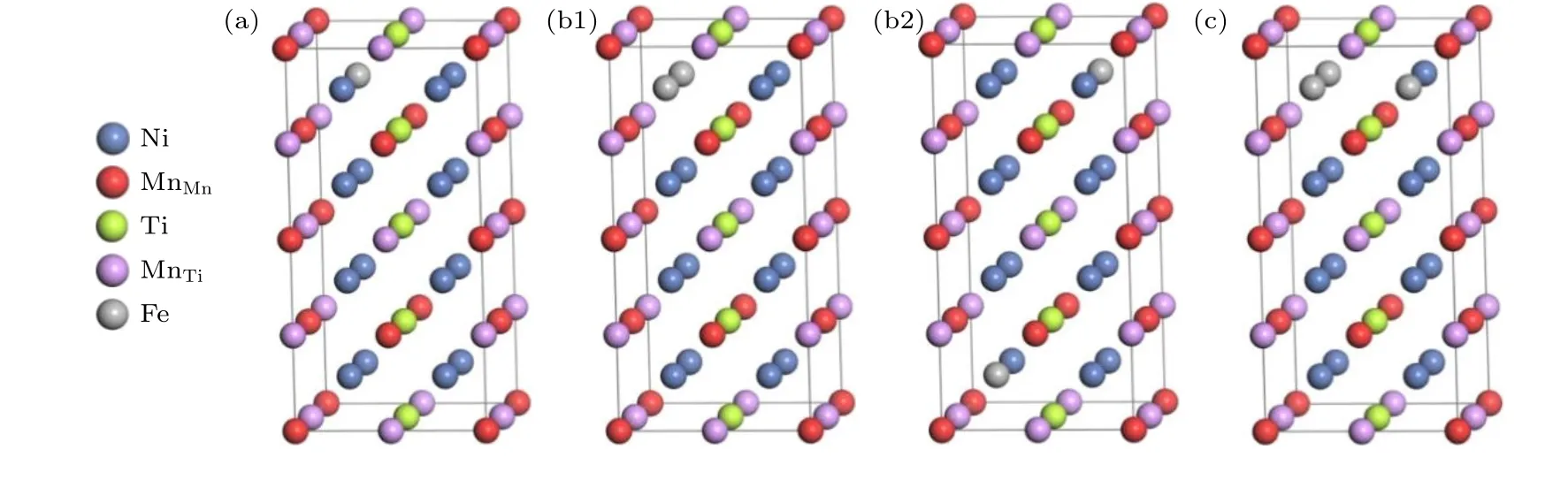
图1 Ni50—xMn37.5Ti12.5Fex (x=3.125,6.25,9.375)合金系奥氏体相的原子占位方式 (a) x=3.125;(b1) x=6.25,聚集分布;(b2) x=6.25,离散分布;(c) x=9.375Fig.1.Atomic occupancy of austenitic phase in Ni50—xMn37.5Ti12.5Fex (x=3.125,6.25,9.375) alloys: (a) x=3.125;(b1) x=6.25,aggregated distribution;(b2) x=6.25,distant distribution;(c) x=9.375.

由于马氏体相变为无扩散式共格切变,可知马氏体相变前后原子间的近邻关系不变,即在奥氏体相中Fe 的原子位置确定后,马氏体相中的原子位置关系也随即确定.为了更加直观的表现Fe在Ni50—xMn37.5Ti12.5Fex合金系中的占位情况,不同掺杂浓度的Fe 原子在Ni50—xMn37.5Ti12.5Fex合金系奥氏体中的分布模型如如图1(a)、图1(b1)和图1(c)所示.

为了确定合金系奥氏体和马氏体相的磁性状态,计算了不同磁性状态下的奥氏体相和马氏体相的形成能,在计算过程中考虑了铁磁性和反铁磁性两种情况.如图2 所示,随着Fe 掺杂量的增加,FA的能量始终低于AFA,表明Ni50—xMn37.5Ti12.5Fex(x=3.125,6.25,9.375)合金系的奥氏体相倾向于呈现铁磁性,此时奥氏体相中的MnMn原子的磁矩与MnTi原子的磁矩呈现平行排列.对于马氏体相,FM 的形成能始终高于AFM,表明马氏体将会以反铁磁态的形式存在,马氏体相中的MnMn磁矩与MnTi磁矩呈现反平行排列.因此,后续的所有计算均是针对铁磁性奥氏体和反铁磁性马氏体开展.

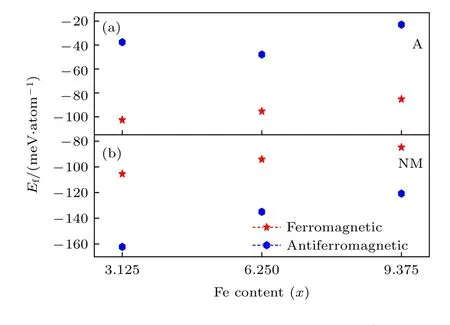
图2 Ni50—xMn37.5Ti12.5Fex (x=3.125,6.25,9.375)合金系在铁磁性和反铁磁性下的形成能 (a) 奥氏体相;(b) 马氏体相Fig.2.The Ef for Ni50—xMn37.5Ti12.5Fex (x=3.125,6.25,9.375) alloys in ferromagnetic and antiferromagnetic: (a) Austenite;(b) martensite.

形成能是固态物质相稳定性的表征方法[32],被定义为化合物的基态总能减去相关元素在它们的纯金属块体参考态下的总能,并将所有的能量归一化.为了确定Fe 原子的掺杂量对Ni50—xMn37.5Ti12.5Fex合金系奥氏体和马氏体相稳定性的影响情况,计算了合金系奥氏体与马氏体相的形成能,结果如图3(a)所示.奥氏体相和马氏体相的Ef均随着Fe 原子掺杂量的增加而逐渐增大,说明Fe 原子的掺杂将会降低奥氏体和马氏体的相稳定性.由于掺杂原子与基体原子的半径和电负性等因素的差异,第四组元Fe 的掺杂必然会导致局部的晶格畸变.在结构优化的过程中,为了保持原有立方结构,形成能逐渐增大,导致合金相稳定性将逐渐降低.另外,在不同成分下,马氏体相的形成能都远低于奥氏体相,说明马氏体相比奥氏体相更稳定,Ni50—xMn37.5Ti12.5Fex(x=3.125,6.25,9.375)合金系可以发生从铁磁性奥氏体到反铁磁马氏体的磁-结构耦合转变,这为调控合金的磁热效应奠定了坚实的基础.

本文进一步计算了Ni50—xMn37.5Ti12.5Fex合金系的奥氏体与马氏体相之间的能量差ΔE、电子浓度e/a和电子密度n以衡量马氏体相变驱动力的大小并揭示马氏体相变温度随成分的变化规律[33],如图3(b)所示.随着Fe 掺杂量的增加,能量差ΔE呈现下降趋势,说明马氏体相变驱动力不断减小;但ΔE始终为正,这表示在研究范围内的合金成分始终能够发生马氏体相变.ΔE对马氏体相变温度的变化趋势具有预测作用,即ΔE越小,对应的马氏体相变温度越低.另外,Fe 原子的价电子数小于Ni 原子,随着Fe 掺杂量的增加,Ni50—xMn37.5Ti12.5Fex合金系的电子浓度e/a呈现下降趋势.与成分相关的马氏体相变温度与电子浓度e/a几乎呈线性关系[34].然而,由于电子浓度e/a并非是影响马氏体相变温度的唯一因素,Chen 等[35]提出了电子密度来综合说明电子浓度e/a、单胞内的原子数N和晶胞体积Vcell对马氏体相变温度的影响.如表1 所列,随着Fe 掺杂量的增加,电子浓度e/a和电子密度n的减小意味着马氏体相变温度的下降,这与ΔE相变驱动力的预测结果一致.

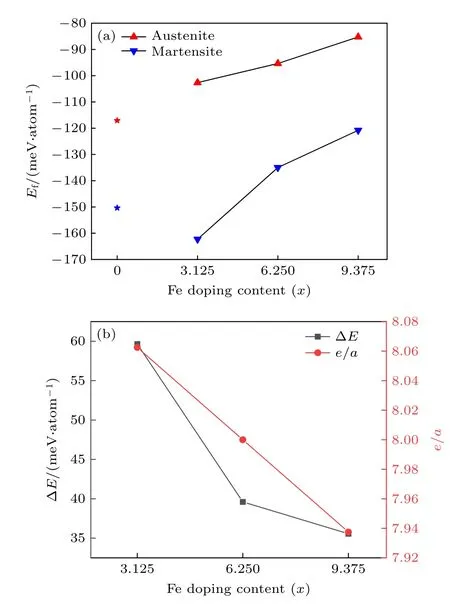
图3 (a) Ni50—xMn37.5Ti12.5Fex (x=3.125,6.25,9.375)合金系的形成能随Fe 掺杂含量的变化趋势;(b) Ni50—xMn37.5 Ti12.5Fex (x=3.125,6.25,9.375)合金系奥氏体和马氏体的能量差ΔE 和电子浓度e/a 随Fe 掺杂量的变化Fig.3.(a) Ef of Ni50—xMn37.5Ti12.5Fex (x=3.125,6.25,9.375)alloys;(b) variation of energy difference ΔE and e/a of Ni50—xMn37.5Ti12.5Fex (x=3.125,6.25,9.375) alloys with Fe doping content.

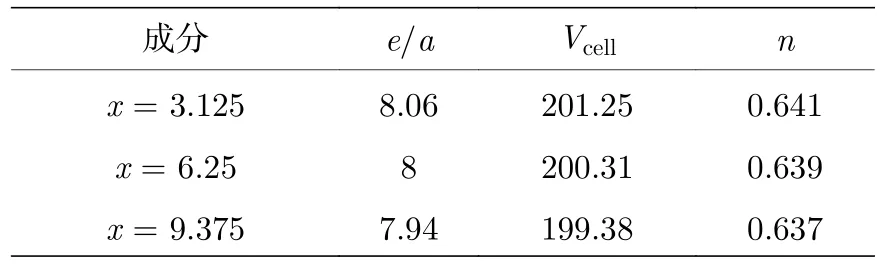
表1 Ni50—xMn37.5Ti12.5Fex (x=3.125,6.25,9.375)合金系的电子浓度e/a、晶胞体积Vcell 和电子密度nTable 1.Electron concentration (e/a),the cell volume (Vcell),and density of electrons (n) of Ni50—xMn37.5 Ti12.5Fex (x=3.125,6.25,9.375) alloys.

在确定了奥氏体相与马氏体相的磁性状态以及马氏体相变情况后,计算了合金系铁磁性奥氏体和反铁磁性马氏体的晶格常数和原子间距,计算结果分别见表2 和图4.如表2 所列,Ni50—xMn37.5Ti12.5Fex合金系奥氏体相的晶格常数随着Fe 掺杂量的增加而减小,尽管Fe 的原子半径(1.26 Å)略大于Ni 的原子半径(1.24 Å)[36],但Fe 原子的磁矩远大于Ni 原子的磁矩,在磁性与原子半径两个因素的共同作用下,奥氏体中Mn-Mn 和Mn-Fe 之间的原子间距明显减小,如图4(a)所示,导致奥氏体相晶格常数的减小.这种现象在Fe 取代Ni 的Mn2NiGa 合金中曾被报道[36].

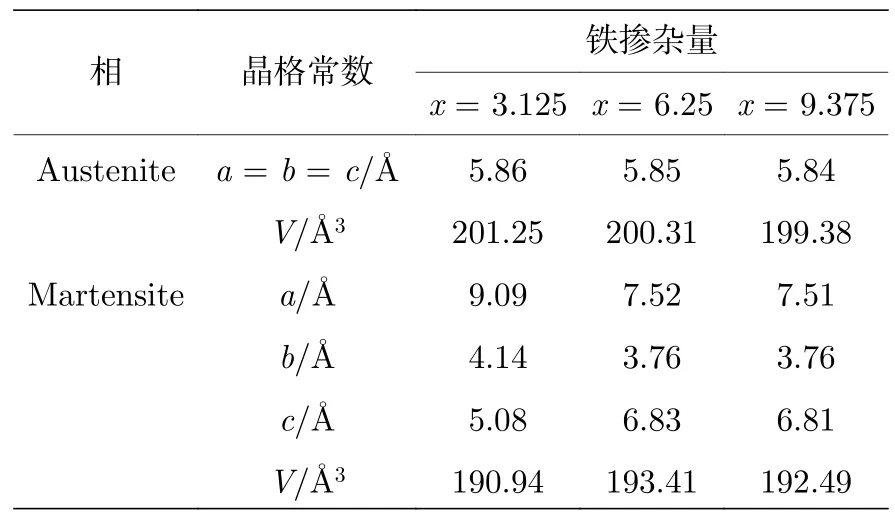
表2 Ni50—xMn37.5Ti12.5Fex (x=3.125,6.25,9.375)合金系的平衡晶格常数Table 2.Equilibrium lattice parameters of Ni50—xMn37.5 Ti12.5Fex (x=3.125,6.25,9.375) alloys.

从表2 中可知,Ni50—xMn37.5Ti12.5Fex合金系的马氏体相的晶格常数a,b随着Fe 掺杂量的增多而呈现减小趋势,晶格常数c增大,导致四方畸变度c/a和c/b升高.马氏体的体积则随着Fe 掺杂量的增多先增大后减小,而马氏体相中的Mn-Mn 间距呈现先增大后减小的趋势,如图4(b)所示,这是由于Mn 原子具有较大的原子半径(1.27 Å),同时也具有较大的磁性,对晶格体积的影响较大.此外,Ni50—xMn37.5Ti12.5Fex(x=3.125,6.25,9.375)合金系奥氏体相的体积均大于对应成分马氏体相的体积,表明在马氏体相变过程中合金体积发生了收缩将产生宏观形变.

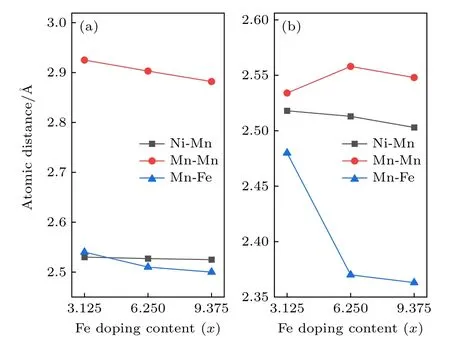
图4 Ni50—xMn37.5Ti12.5Fex (x=3.125,6.25,9.375)合金系的原子间距 (a) 奥氏体;(b) 马氏体Fig.4.Atomic distance of Ni50—xMn37.5Ti12.5Fex (x=3.125,6.25,9.375) alloys: (a) Austenite;(b) martensite.

3.2 磁性能

为了揭示Ni50—xMn37.5Ti12.5Fex(x=3.125,6.25,9.375)合金系奥氏体和马氏体相的磁性能随合金成分的变化规律,本节详细地计算了合金系两相的总磁矩以及原子磁矩,如图5 所示.奥氏体相为铁磁性,其磁矩约为6.3µB/f.u.,马氏体相为反铁磁性,其磁性几乎为零.奥氏体和马氏体相的总磁矩随着Fe 掺杂量的增加基本保持不变,表明两相的磁性受Fe 原子的影响较小.铁磁奥氏体相的磁矩远大于反铁磁马氏体相的磁矩,表明在马氏体相变过程中伴随大的磁化强度差ΔM,大的ΔM有利于Ni50—xMn37.5Ti12.5Fex合金在较低的磁场下获得磁热效应.

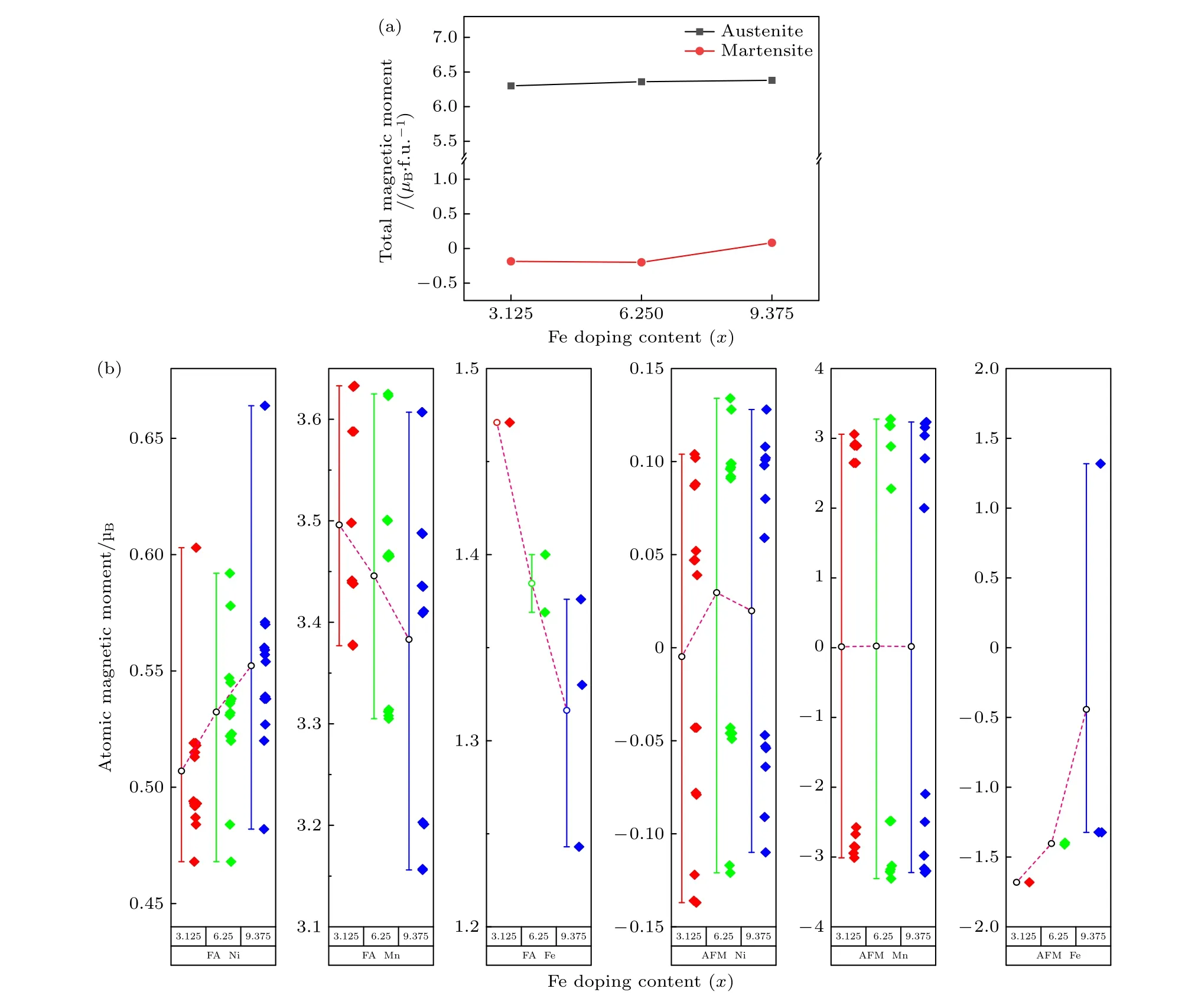
图5 (a) Ni50—xMn37.5Ti12.5Fex (x=3.125,6.25,9.375)合金的总磁矩;(b) Ni50—xMn37.5Ti12.5Fex (x=3.125,6.25,9.375) 合金的原子磁矩Fig.5.(a) Total magnetic moments of Ni50—xMn37.5Ti12.5Fex (x=3.125,6.25,9.375) alloys;(b) atomic magnetic moments of Ni50—xMn37.5Ti12.5Fex (x=3.125,6.25,9.375) alloys.

Ni50—xMn37.5Ti12.5Fex合金系的Mn-Mn 原子间距示于图4 中.从图4 可知,铁磁性奥氏体相中的Mn-Mn 原子间距为2.925—2.882 Å,而反铁磁马氏体相中的Mn-Mn 原子间距为2.558—2.534 Å.可以看出,合金磁性的改变与Mn-Mn 间距密切相关.当Mn-Mn 间距减小时,Mn-Mn 3 d 轨道电子交互作用增强,将会导致MnMn原子和MnTi原子间出现反铁磁耦合现象,这也是Ni50—xMn37.5Ti12.5Fex合金系的马氏体相呈现反铁磁性的本质原因.

从图5(b)可以看出,在奥氏体相中,随着Fe含量的增加,Ni 的原子磁矩增加.这主要是由Ni-Mn 原子间距减小导致的.Ni-Mn 间距减小,导致Ni 3d 和Mn 3d 轨道电子的耦合作用增强,进而导致Ni 原子磁矩增大.奥氏体中Mn 的平均原子磁矩约为3.4—3.5µB,并且MnMn与MnTi的原子磁矩呈现平行排列方式,使得Mn 原子能够表现出较强的磁性.而在马氏体相中,MnMn原子与MnTi原子的磁矩呈现反平行排列,导致Mn 原子的平均磁矩几乎为零.而Ni 的原子磁矩是由Mn 磁矩诱导的,平均磁矩为0 的Mn 环境使得Ni 原子磁矩也近乎为0.这些因素共同导致Ni50—xMn37.5Ti12.5Fex合金系的马氏体相呈现为反铁磁性,总磁矩几乎为零.

3.3 电子结构

为了探究Ni50—xMn37.5Ti12.5Fex合金系的磁性能和马氏体相变的起源,本节对合金系中奥氏体和马氏体相的电子结构进行了详细的研究,使用布洛赫四面体法[37]计算了合金系两相的总电子态密度(TDOS)和分波电子态密度(PDOS),结果如图6和图7 所示.

图7 Ni50—xMn37.5Ti12.5Fex (x=3.125,6.25,9.375)合金系的分波电子态密度 (a) x=3.125;(b) x=6.25;(c) x=9.375Fig.7.PDOS of Ni50—xMn37.5Ti12.5Fex (x=3.125,6.25,9.375)alloys: (a) x=3.125;(b) x=6.25;(c) x=9.375.

合金的磁矩主要由费米面以下的自旋向上和自旋向下的电子数之差决定.从图6 可以看出,随着Fe 掺杂量的增加,奥氏体和马氏体相的TDOS中的电子分布基本没有变化,奥氏体相TDOS 的自旋向上和自旋向下部分的对称性低,使奥氏体相TDOS 的上下自旋部分的电子数之差大,从而导致奥氏体相具有强铁磁性.马氏体相TDOS 的自旋向上和自旋向下的部分对称性高,使马氏体相TDOS 的上下自旋部分的电子数之差接近0,这也是马氏体相磁性表现弱磁性的根本原因.

图6 Ni50—xMn37.5Ti12.5Fex (x=3.125,6.25,9.375)合金系的总态密度 (a) x=3.125;(b) x=6.25;(c) x=9.375Fig.6.TDOS of Ni50—xMn37.5Ti12.5Fex (x=3.125,6.25,9.375) alloys: (a) x=3.125;(b) x=6.25;(c) x=9.375.

为了探究Ni50—xMn37.5Ti12.5Fex合金系的马氏体相变情况受Fe 掺杂量影响的本质,对Ni50—xMn37.5Ti12.5Fex合金系的奥氏体和马氏体相在费米面处的TDOS 进行更加详细的比较.奥氏体相的TDOS 在费米面附近自旋向下的部分存在态密度的凸起,这样的电子结构代表较低的结构稳定性,众多研究数据表明,在费米面附近的态密度峰是马氏体相变的重要诱因[38-40].奥氏体转变为马氏体相的过程中伴随着态密度在费米面附近自旋向下部分的态密度峰发生劈裂的现象,使马氏体相的费米面处于态密度波谷中,导致马氏体相的电子结构比奥氏体相更稳定,这就是Jahn-Teller 劈裂效应.图6 中马氏体相的TDOS 在费米面附近自旋向下部分的峰值强度始终低于奥氏体相的峰值强度,表明在Ni50—xMn37.5Ti12.5Fex合金系中能够发生马氏体相变,这与上文通过形成能结果所得结论一致.

为了揭示Ni50—xMn37.5Ti12.5Fex合金系相稳定性和磁性能随Fe 掺杂量的变化机理,对合金系奥氏体相和马氏体相的Ni,MnMn,MnTi以及Fe 原子的3 d 电子分波态密度进行了详细的研究,结果如图7 所示.奥氏体相中各原子的自旋向上与自旋向下的电子分布对称性差,使奥氏体相表现为铁磁性.奥氏体相的TDOS 在费米面以下的自旋向下部分的电子分布主要由Ni 和Fe 的3 d 电子贡献,而自旋向上部分的电子分布主要由Ni,Mn 和Fe 的3 d 电子共同贡献,并且Ni 原子与Mn 原子在—1 到—2 eV 范围内发生明显的杂化现象,证明Ni原子与Mn 原子之间存在强烈的d-d 键合作用.值得注意的是,奥氏体相的TDOS 在费米面以上部分的电子分布主要由MnMn原子与MnTi原子贡献,并且两种Mn 原子的电子分布一致,说明MnMn原子与MnTi原子的磁矩平行排列,使Mn 原子具有强铁磁性.

在马氏体相中,Ni 原子的自旋向上和自旋向下部分的电子分布对称性较高,使Ni 原子磁矩近乎为0.MnMn原子和MnTi原子的电子分布则完全相反,导致了MnMn原子和MnTi原子的磁矩呈现反平行分布.Fe 原子的自旋向上和自旋向下部分的电子分布对称性较差,使其具有一定磁性,但是Fe 原子在合金中的掺杂量较少,无法对马氏体相的磁性状态产生较大影响.

4 结论

本文采用第一性原理计算的方法研究了Ni50—xMn37.5Ti12.5Fex(x=3.125,6.25,9.375)合金系奥氏体相和马氏体相的晶格常数、形成能、磁性能和电子结构,得到的主要结论如下: 在Ni50—xMn37.5Ti12.5Fex合金系中,随着Fe 掺杂量的增多,奥氏体的晶格常数逐渐减小;奥氏体和马氏体相的稳定性均随着Fe 掺杂量的增加而逐渐降低.在不同成分下,马氏体始终比奥氏体形成能更低,表明合金可以发生马氏体相变;合金两相的能量差ΔE、电子浓度e/a和电子密度n都呈现减小趋势,表明马氏体相变驱动力降低,对应的马氏体相变温度将会随着Fe 原子掺杂量的增多而下降.合金的奥氏体呈现铁磁性,马氏体表现为反铁磁性.在马氏体相变后,Mn-Mn 原子间距减小,MnMn原子与MnTi原子磁矩呈反平行排列导致总体磁性几乎为0.两相的磁性受Fe 原子掺杂量的影响均较小;马氏体相在费米面处的电子态密度峰值低于奥氏体相,表明马氏体相拥有比奥氏体相更稳定的电子结构.奥氏体相向马氏体转变的过程中,在费米面附近自旋向下的态密度的峰值存在Jahn-Teller 劈裂效应.

感谢山西省超级计算中心“天河二号”提供的技术支持.