基于改进蝙蝠算法的装配式施工安全风险优化
2023-03-04常春光代宾宾邓云兵卢禹先
常春光,代宾宾,邓云兵,卢禹先
(1.沈阳建筑大学管理学院,辽宁 沈阳 110168;2.上海宝冶集团有限公司,上海 201941)
国家发展战略打开了建筑工业化发展的新局面,使装配式建筑得到了良性发展,但施工安全风险问题也随之而来,安全风险的存在可能会造成人员和经济的双重损失。因此,实现装配式建筑施工安全风险的有效控制是建筑工业化进程中亟待解决的难题。在工程建设中,管理人员要结合实际分析每个施工阶段风险要素,尽可能减少施工过程中的安全隐患,实现事前控制、事中监管、事后反馈的全周期安全管理。
国内外学者对装配式建筑施工的优化进行了大量研究,马辉等[1]以装配式建筑吊装施工空间冲突为研究对象,构建优化模型,实现了对装配式建筑吊装施工空间的优化管理。LI等[2]分析了可能对装配式建筑的施工进度产生重大影响的风险因素,并对不同的利益相关者提出相应的决策以降低装配式建筑的施工进度风险。
蝙蝠算法作为一种新型智能算法广泛应用于处理工程优化、模型识别等方面,但其存在易陷入局部极值、收敛精度低等缺点。近年来,国内外学者采取多种方式对其进行改进,以达到增强算法性能的目的。裴宇航等[3]为了加快蝙蝠算法的收敛速度和寻优精度,提出一种动态调整惯性权重的自适应蝙蝠算法。RAMLI等[4]通过修正维数和提供惯性权重来改进蝙蝠算法,发现改进蝙蝠算法在寻找最优解方面更有效,同时提高了结果的质量和收敛速度。
在对基本蝙蝠算法进行系统研究基础上,研究提出一种加入了logistic混沌映射和指数递减的惯性权重的改进蝙蝠算法,将其运用到解决装配式建筑施工安全风险优化问题中,通过将实际装配式工程项目代入到模型中来验证模型与算法的适配性,最后为装配式建筑施工安全管理提供更好的决策方案。
一、装配式施工安全风险识别量化
1.装配式施工安全风险的识别
风险识别是进行风险量化的前提,是实现风险管理的重要基础[5],装配式建筑施工过程技术要求较高,风险产生的可能性较大,在进行装配式建筑施工安全风险识别时要考虑各个阶段的每个方面,多角度地对风险目标进行识别。因此,选用工作分解结构-风险分解结构(Work Breakdown Structure-Risk Breakdown Structure,WBS-RBS)法进行风险识别能够精准识别出风险因素。
利用WBS-RBS法对装配式建筑施工安全风险进行识别时,主要有以下3个步骤:
(1)构建WBS。根据装配式建筑的施工特点,将整个施工过程分为16项工序。即A1为构件入场及施工准备、A2为放线及测量定位、A3为预制墙体吊装、A4为斜支撑安装、A5为套筒灌浆、A6为节点区钢筋绑扎与支模、A7为现浇墙体钢筋绑扎与支模、A8为现浇梁钢筋绑扎与支模、A9为预制叠合板吊装与支撑、A10为预制楼梯吊装及搭接处理、A11为预制阳台吊装及接缝处理、A12为预制空调板吊装与接缝处理、A13为现浇板底钢筋绑扎、A14为水电线管预埋、A15为梁板面筋绑扎、A16为结构钢筋混凝土浇筑。
(2)构建RBS。将装配式建筑施工安全风险按照人为风险、物的风险、技术风险、环境风险、管理风险筛选出22个风险因素[6]。R1为人员素质水平、R2为人员安全意识、R3为预制构件验收、R4为构件运输与存放规范程度、R5为机具选择、R6为临时支撑及防护情况、R7为构件质量、R8为材料性能、R9为拉节点可靠程度、R10为吊装连接强度、R11为施工组织设计、R12为措施搭拆技术、R13为安装技术成熟度、R14为搭接精度、R15为临时固定措施、R16为工艺技术操作水平、R17为平面布置合理性、R18为地质条件勘察情况、R19为预埋节点定位准确度、R20为施工现场环境、R21为测量计划合理性、R22为安全管理制度。
(3)构建WBS-RBS耦合矩阵。以WBS为行、RBS为列建立耦合矩阵,识别出每项施工工序中的具体风险因素(见表1)。

表1 施工工序风险因素
2.装配式施工安全风险的量化
风险的量化是由风险发生概率与风险带来的影响共同实现,其中风险带来的影响用风险损失值来表示。
(1)模糊贝叶斯网络图
贝叶斯网络图是以贝叶斯概率为基础的有向无环图,包括变量节点及连接这些节点的有向边组成的网络化图形和表达节点之间关系强度的条件概率表。设R1、R2为工程项目的两个风险源,每个风险源具有两种状态(发生和不发生),R1、R2共同影响工程项目A1阶段产生的风险,则R1、R2和A1之间产生的关系如图1所示。
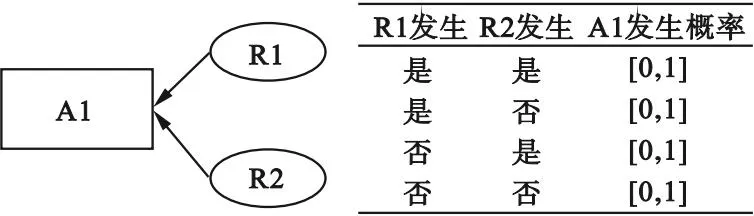
图1 贝叶斯网络示意图
由于风险因素的状态难以通过数据直接得到,因此采用三角模糊数[7]求解风险因素(根节点)的先验概率和施工工序(中间节点)的条件概率。通过对专家问询有关装配式施工过程中的风险发生可能性,设置发生概率分别处于[0,20)、[20,40)、[40,60)、[60,80)、[80,100]时所对应的语意变量分别为“很小可能发生”“较小可能发生”“可能发生”“较大可能发生”“很大可能发生”,并设计相应的问卷分数与三角模糊数值,得出风险发生概率的语意变量(见表2)。
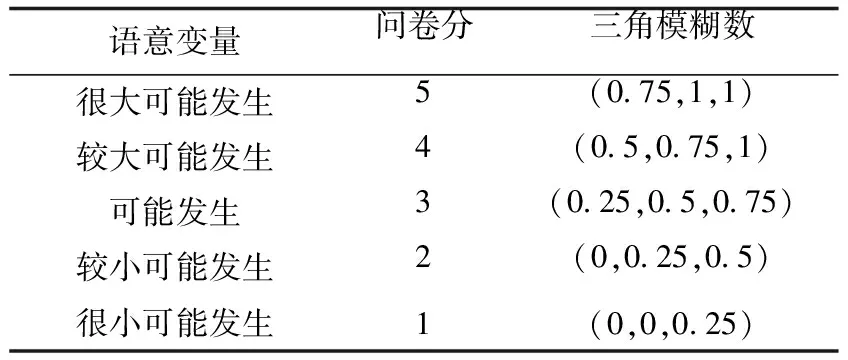
表2 事件发生概率的语意变量
为了得出相对合理的模糊概率,利用算术平均法求出多位专家的评判结果。
(1)
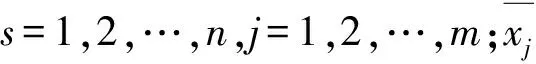
根据式(2)对获得的节点模糊概率进行解模糊,将各节点从模糊数转化为明确数。
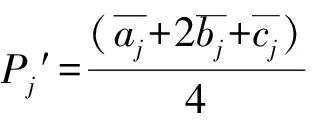
(2)
式中:Pj′为第j个节点去模糊化的明确概率。
(2)基于施工网络计划图的风险传递
任何一个施工项目从开始到结束的过程是由若干道工序构成的网络结构,各道工序之间存在着密切联系。施工过程中的风险会随着网络结构中的链式结构传递给下一道工序,在装配式建筑施工过程中,风险的传递通过施工网络计划图来实现(见图2)。
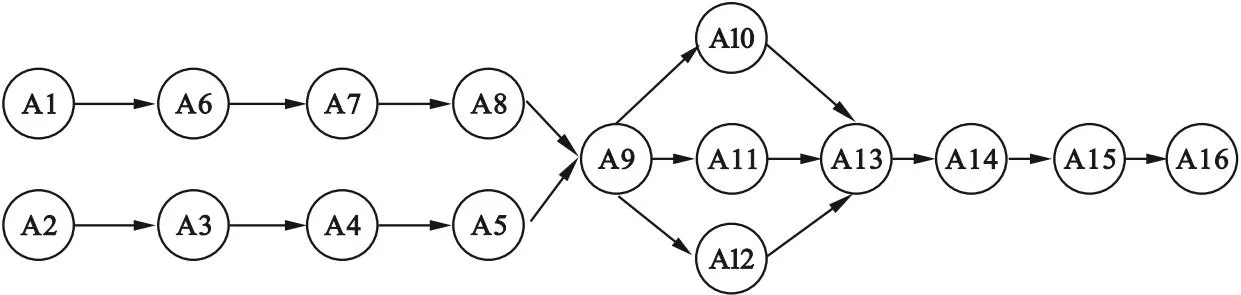
图2 施工网络计划流程
除首道工序外,其后的每道工序的风险均包括两部分:一是自留风险,即本道工序由于自身所处环境而产生的风险;二是转移风险,即相邻上道工序的风险传递给本道工序的风险。每道工序的风险一部分自留,另一部分通过链式结构传递给下一道工序。计算公式为
Pi=Pi-1×λi+Pi′×(1-λi)
(3)
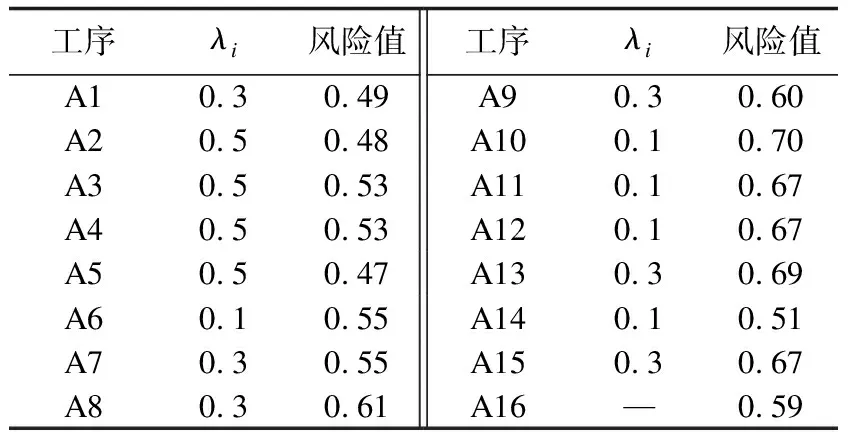
式中:Pi为第i项工序考虑了风险传递后的风险发生概率值;Pi′为第i项工序未考虑风险传递后的风险发生概率值;λi为风险系数,该系数通过构建模糊评价集确定得出(见表3)。

表3 λi模糊评价集
(3)风险损失值的构造
风险损失值的构造采用多属性风险损失比例函数[8]。对于多属性效用函数来说,在每个单属性的效用达到最优时,该多属性效用函数发挥的作用就最大。因此将此思维逆向应用到多属性风险损失比例函数之中,即在工期最长、成本最大、质量最劣时风险损失值最大,反之产生的风险损失值最小,因此通过构造多属性风险损失比例函数就可将风险损失值L与工期T、成本C、质量Q联系在一起。针对工序i,Li=L(Ti,Ci,Qi),其中,工期Ti、成本Ci和质量Qi为多属性变量,可以采用如式(4)~ 式(7)所示的加式分解形式。
Li(Ti)=ai+bi(Ti-Timax)2
(4)
Li(Ci)=hi+di(Ci-Cimax)2=hi+
(5)
Li(Qi)=ei+fi(Qi-Qimin)2=ei+
fi(μi×(Qimax-βi×(Ti0-Ti)2)+
(1-μi)Qimax-Qimin)2
(6)
L=Li(Ti,Ci,Qi)=kT×Li(Ti)+
kC×Li(Ci)+kq×Li(Qi)=kT×(ai+
bi(Ti-Timax)2)+kC×(hi+
kQ×(ei+fi(μi×(Qimax-βi×(Ti0-Ti)2)+
(1-μi)Qimax-Qimin)2)
(7)
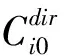
二、安全风险优化模型的构建
1.问题描述
装配式建筑施工过程中成本的投入量与工期的长短都影响着风险的发生程度。低成本的投入会使得施工过程中的风险值上升。缩短工期可能带来质量问题,而质量问题出现将直接带来风险损失。因此在实现装配式建筑施工安全风险控制的过程中,要考虑整个施工过程工期、成本和质量的约束,即在合理范围内将风险损失值控制在最小。
2.模型构建
(1)参数与变量设置
(2)模型的建立
建立以实现风险损失值最小为目标函数,以控制工期-成本-质量的投入为约束条件的装配式建筑施工安全风险控制模型,如式(8)、式(9)
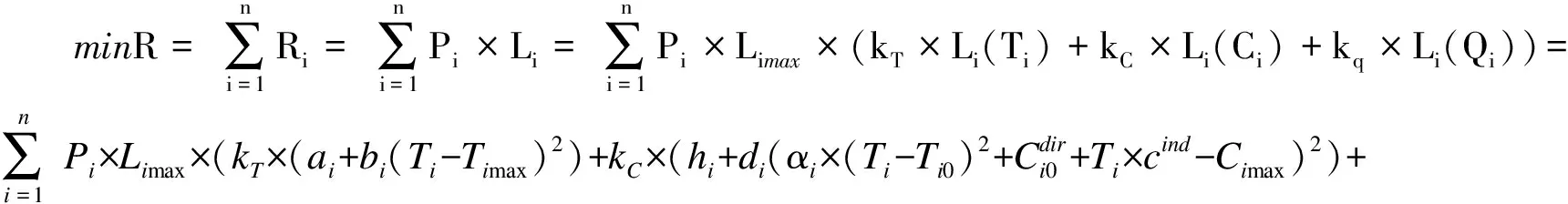
(8)
(9)
式中:式(8)为目标函数,表示风险损失值最小;式(9)每行分别为第i项工序的施工工期范围、第i项工序的施工成本范围、第i项工序的施工相对质量水平范围、整个项目的施工工期上限、整个项目的施工成本上限、整个项目的施工相对质量水平下限。
3.罚函数对约束条件的处理
罚函数[9]是解决约束优化问题的一种有效方法。其惩罚策略是:在无约束的情况下对违反约束条件的迭代点赋予很大的数,使得其目标函数值很大,之后在不断寻找最小解的过程中把违反约束条件的值舍去,直到收敛到原来约束最优化的极小值点。利用罚函数将安全风险优化模型转化为无约束的模型如式(10)~式(19)
(10)
g1(T)=Timin-Ti
(11)
g2(T)=Ti-Timax
(12)
Ti×cind
(13)
Ti×cind-Cimax
(14)
g5(T)=Qimin-(Qimax-βi×
(Ti0-Ti)2)
(15)
g6(T)=Qimax-βi×(Ti0-Ti)2-Qimax
(16)
(17)
Ti×cind-Cn
(18)
βi×(Ti0-Ti)2)+(1-μi)Qimax)
(19)
式中:σ为惩罚因子,是一个正数;gi(T)为变量T违反约束的程度。
三、蝙蝠算法及其改进
1.蝙蝠算法
蝙蝠算法是Yang 基于群体智能提出的启发式的搜索算法,模型简单、参数少,收敛速度快,因此常用来解决优化问题。
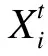
fi=fmin+(fmax-fmin)β
(20)
(21)
(22)
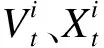
当蝙蝠个体局部寻优时,在当前搜索到的最优解附近实施局部搜索,生成[0,1]之间的随机数rand,若rand>ri(蝙蝠i的脉冲发射率),则实施如下局部搜索策略,产生新解Xnew如式(23)
Xnew=X*+εAt
(23)
式中:ε为[-1,1]之间的均匀分布的随机数;At为整个群体在t时刻的平均响度;Xnew为群体中产生的新局部解。
(24)
(25)
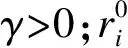
2.蝙蝠算法的改进
(1)logistic混沌映射初始化种群
混沌是自然界所特有的一种无周期现象,由于混沌的遍历性,它能够不重复地将变量随机均匀地映射到优化空间。蝙蝠算法中初始种群个体的生成具有较大的随机性,因此利用混沌变量进行优化搜索比盲目无序的随机搜索更具优越性。由于logistic方法原理简单,优化能力强,故多用其进行种群的初始化,数学表达式如式(26)~式(27)
Yn+1=a*Yn(1-Yn)
(26)
Xi=Lb+(Ub-Lb)*Yn
(27)
式中:Yn∈[0,1]为混沌变量;a∈[0,4]为logistic参数;Xi为蝙蝠i的位置;Lb为搜索空间的下限;Ub为搜索空间的上限。
(2)加入指数递减惯性权重
根据蝙蝠算法的速度更新公式可以看出速度项系数恒定为1,因此迭代前期蝙蝠搜索的敏感性较差,很容易在前期陷入局部极值,短时间内无法跳出,从而导致算法在进行全局搜索和局部搜索时缺乏平衡性。
因此选取指数递减惯性权重[11]对基本蝙蝠算法速度更新公式进行改进如式(28)、式(29)
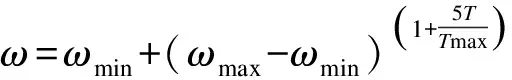
(28)
(29)
式中:ωmax和ωmin为ω的最大和最小值;T为迭代次数;Tmax为最大迭代次数。
设置参数:ωmax=0.9,ωmin=0.4,Tmax=500,ω-T函数图像如图3所示。
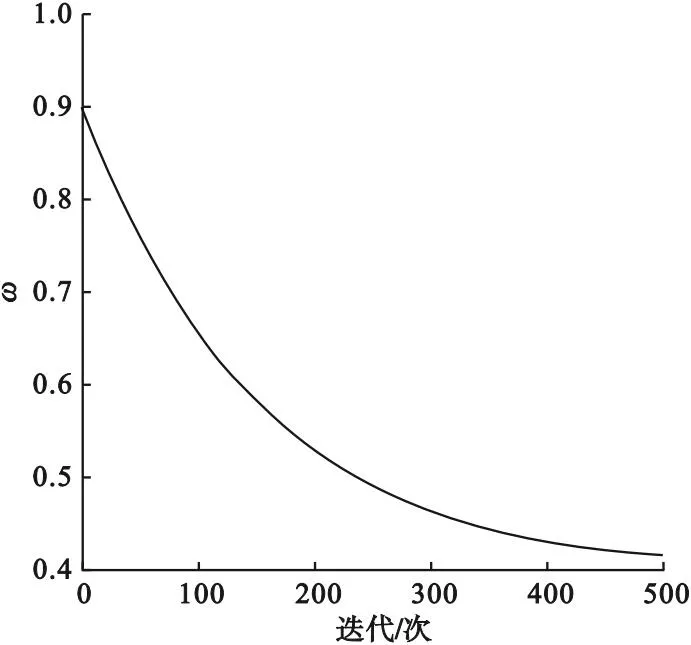
图3 ω-T函数图
该策略使惯性权重ω在迭代初期以较快速度减小,使算法迅速收敛,而在迭代后期使ω以较慢速度减小,有利于算法局部精确搜索。
3.改进蝙蝠算法的流程步骤
①设置参数:蝙蝠的种群规模N,最大迭代次数Tmax,脉冲频率范围[fmin,fmax],初始脉冲响度A0,初始脉冲发射速率r0,音量衰减系数θ,脉冲频度增强系数γ,最大和最小惯性权重ωmax和ωmin;
②利用式(26)、式(27)进行logistic混沌映射的结果作为蝙蝠种群初始位置Xi根据适应度函数f(x)寻找出最优值,并计算当前全局搜索最优位置解X*;
③根据式(20)、式(22)、式(28)、式(29)更新蝙蝠的速度和位置;
④产生一个随机数rand,如果rand>ri,则代入式(23)在局部搜索过程中产生一个新解;
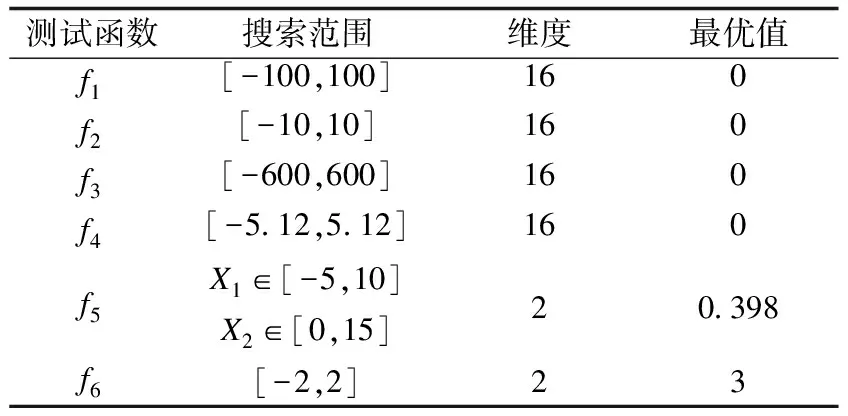
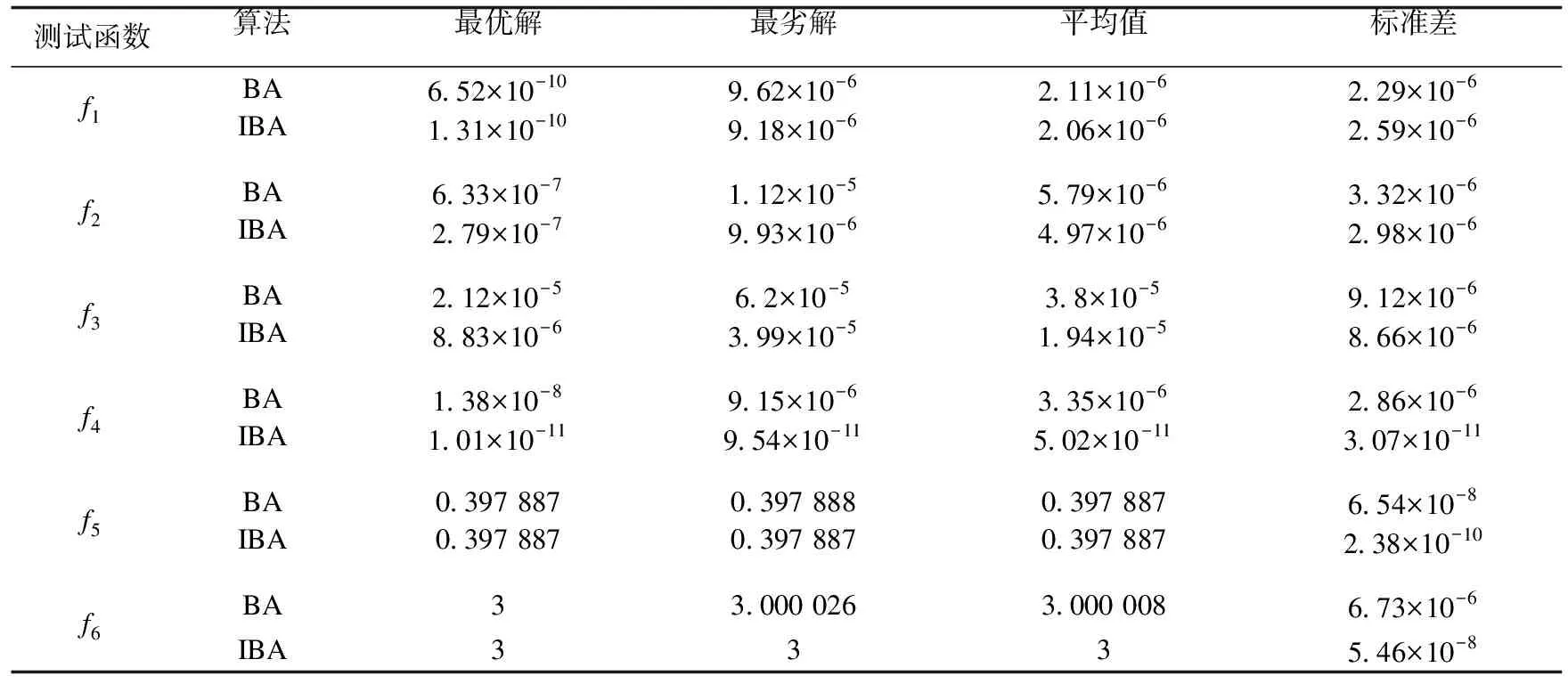
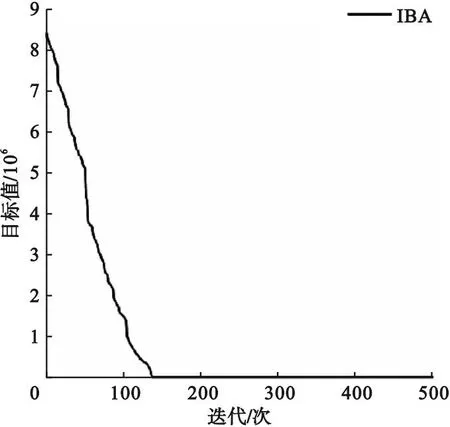
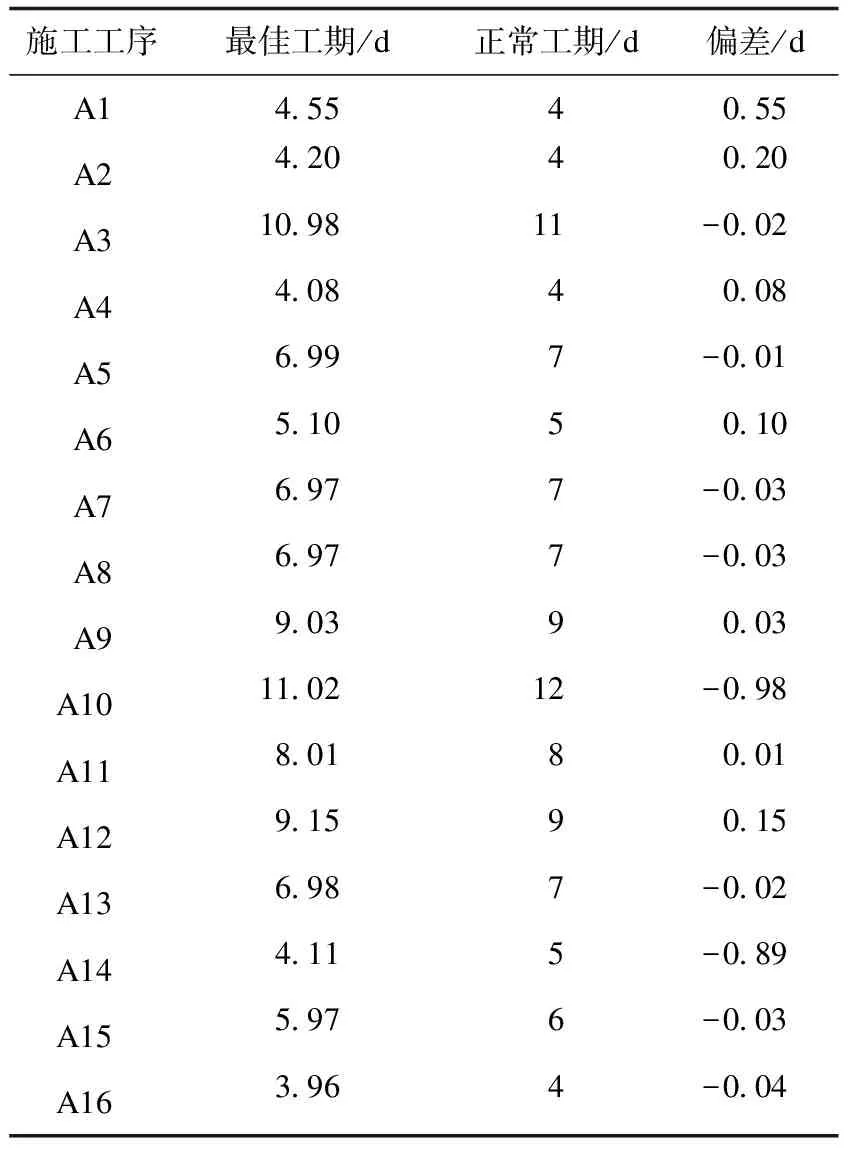
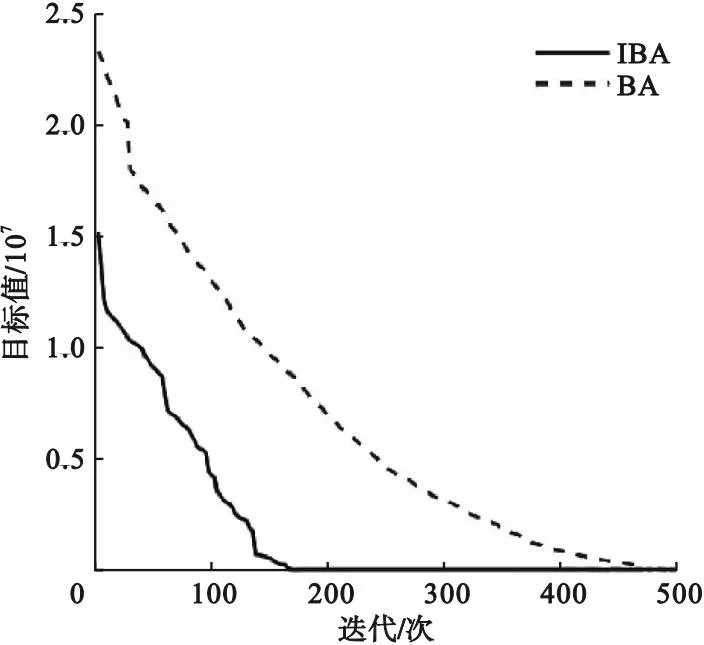
⑤产生一个随机数rand,如果rand ⑦重复步骤②~⑥的迭代过程,直到找到满足搜索精度的最优解或达到最大迭代次数; ⑧输出全局最优解。 为了验证改进蝙蝠算法具有更好的寻优性能,笔者选取了6个标准测试函数(见表4)来对改进蝙蝠算法进行测试,并与基本蝙蝠算法进行比较,对其寻优精度进行分析。6个标准测试函数分别为f1(Sphere)、f2(Schwefel′s problem)、f3(Griewank)、f4(Rastrigin)、f5(Branin)、f6(Goldstein-Price)。 表4 标准测试函数相关参数 为了更加直观地比较算法之间的性能,对基本蝙蝠算法(BA)和改进蝙蝠算法(IBA)设置统一的参数,迭代500次,种群数量为20,为了避免偶然性的误差,重复运行每个标准测试函数的程序30次,记录实验所得的最优解、最劣解、平均值和标准差,并进行算法的寻优性能评价,测试结果如表5所示。 表5 BA与IBA求解测试函数的结果 从表5中可以看出当对每个测试函数进行调试时,IBA的最优解、最劣解、平均值都要优于BA,表明IBA的寻优精度更好。运用IBA进行测试时得到的标准差更小,说明稳定性较好,有利于帮助个体跳出局部最优。综上所述,IBA相比较BA的寻优精度得到了较好的改善。 首先进行风险发生概率的求解。根据三角模糊数求出风险因素的发生概率以及施工工序的条件概率表,利用GeNIE软件构建风险因素贝叶斯网络图,并用施工网络计划图实现施工工序风险的传递。通过调查该装配式建筑施工项目的资料,利用模糊评价集确定各项施工工序的风险传递系数λi,得到考虑风险传递性的各项施工工序风险概率值(见表6)。 表6 施工工序最终风险概率 (1)优化模型求解与结果分析 用IBA求解案例时,首先设置具体参数信息,A0为[0,2]内的随机数,r0为[0,0.05]内的随机数,θ为[0,1]之间的随机数,γ为大于0的随机数,故设置N=40,A0=1,r0=0.05,θ=0.9,γ=0.9,fmax=2,fmin=1,Tmax=500,ωmax=0.9,ωmin=0.4。为了避免结果的偶然性,重复运行程序30次后得到模型最佳施工工期(见表7),得到了目标函数的收敛图(见图4)。 图4 目标函数收敛图 表7 最佳工期 从表7可以看出每项施工工序的最佳工期与正常工期的偏差都是在1 d以内,由于存在成本和质量约束,因此最佳施工工期会与实际施工工期存在一定的偏差。当实际工程项目按照表8中的工期进行实际的施工进度安排时,可以使得产生的风险损失值达到最小。 表8 风险损失值对比 从图4可以看出,IBA在运行到第137次时,寻找到了该目标函数的最优解。目标函数的收敛图的收敛速度很快,利用该算法进行求解实际案例能够快速寻找到近似最优值。 (2)与基本蝙蝠算法求解结果的对比 在同一设置环境下分别用BA和IBA算法进行求解,最后得出风险损失值(见表8)和目标函数收敛图(见图5)。 图5 BA与IBA目标函数收敛图 从表8中可以看出,未优化的风险损失值大概是优化后的2.53倍,因此该数学模型能够在一定程度上实现对风险的优化,降低风险损失值。同时用IBA求出的最优解要比BA求出的最优解小0.72,因此利用IBA求解出的施工工期进行施工,能够降低项目的风险损失。 从图5可以看出,IBA在迭代50次左右就寻找到了最优解,而BA在迭代150次后才寻找到最优解,并且IBA的前期收敛速度明显快于BA,因此采用IBA更有效率和优势,能在较短的时间内寻找到最优解,且更准确、精度更高。 (1)利用logistic混沌映射和加入一种指数递减的惯性权重来进行蝙蝠算法的改进,增加了种群的多样性,提高了基本蝙蝠算法的收敛速度和寻优精度,使得求解性能更加优质高效。 (2)利用改进后的蝙蝠算法求解装配式建筑施工安全风险控制模型,得到了一组最佳施工工期和最小风险损失值,因此在进行实际施工时,可以参考该结果进行装配式施工,合理分配资源。4.实验仿真与结果分析
四、案例分析与模型验证
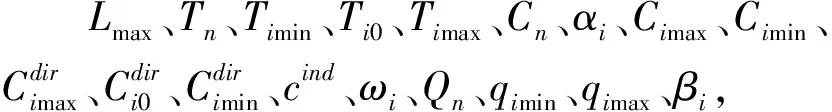
1.风险发生概率的定量分析
2.基于改进蝙蝠算法的案例求解

五、结 论
