不同经济周期中国失业保险最优给付模式探究
2023-03-04徐佳茜
吴 越,徐佳茜
(中央财经大学 保险学院,北京 102206)
一、引言
从2002年的非典型病原体肺炎到2009年蔓延到214 个国家和地区的甲型H1N1 流感,再到2020年的新冠肺炎疫情,21 世纪以来实体经济的发展不断面临着卫生突发事件的挑战。这些无法预料的外部不利冲击快速扰乱了经济秩序,引发了失业率上升、劳动力市场需求不足等问题。此时,政府能否采取科学的宏观调控措施显得尤为重要。失业保险作为社会保障体系的重要组成部分,是许多国家开展劳动力市场调控的核心手段之一。
中国的失业保险制度建立较晚①。截至2022年年底,中国失业保险参保人数仅有23 807万人②,且参保主体以城镇企事业单位职工为主,对拥有较高失业风险的农业生产者以及灵活就业者没有充分的保障。相比之下,瑞士、美国、加拿大等国家的失业保险几乎覆盖了所有受雇人群,对非全日制就业或临时就业人群亦有明确规定。失业保险金替代率(人均失业保险支出占在岗职工平均工资的比例)是国际上衡量失业保险保障水平的重要指标,国际劳工大会在1988 年通过的《促进就业和失业保护公约》中建议,该值不应低于50%。《中国统计年鉴》显示,2021 年我国城镇单位在岗职工月平均工资约为9 284元,而各省每月失业保险金在1 500元上下波动。据此来看,中国的失业保险金替代率距离50%仍有较大差距。
除了覆盖范围较窄与替代率较低等问题外,中国的失业保险制度还存在着给付水平与给付期限调整固化的问题。《失业保险条例》第十八条规定:失业保险金标准应按照低于当地最低工资标准,高于城市居民最低生活保障标准,由省、自治区、直辖市人民政府确定。在给付期限的确定上,我国目前采取的是按月发放形式,所能领取的期限从3 个月到24 个月不等。该期限仅与个人缴费年限挂钩,与失业者年龄、所处经济环境以及失业前的工资水平均无关。由此可见,我国不存在可以根据经济周期波动进行调节的失业保险给付制度。因此建立灵活调整的失业保险制度,讨论在不同经济周期下的失业保险最优给付模式是十分有必要的。
二、文献综述
ANDERSEN 和SVARER[1]的定量研究发现,依赖商业周期的失业保险制度可以有效地提高社会总福利水平。LANDAIS 等[2]也将经济波动加入到失业保险的设计中,建立了不同经济周期下的最优失业保险金模型。但是,不同国家由于其经济体制和失业保险发展水平不同,所采取的调节方式也应有所不同。POLLAK[3]使用生命周期模型对加拿大失业保险制度的研究表明,经济衰退时应该大幅提高失业保险金水平以维护社会稳定。LANDAIS等[4]研究表明最佳的失业保险金替代率是Baily-Chetty 替代率加上一个修正项,该修正项在经济衰退时期为正,而在经济繁荣时期为负,即最优的失业保险调整策略应遵循逆周期原则。BIRINCI等[5]通过构建一个具有总体风险和不完全市场的异质性代理求职模型,认为最优的失业保险金替代率应具有逆周期调节的特点,且其平均水平接近于美国的现行标准。然而MOYEN 和STÄHLER[6]发现这种逆周期政策虽然在美国有可行性,但在欧洲则不然。
与国外研究不同,国内研究主要集中在失业保险金与给付期限调整对失业人员再就业的影响上。这些研究以促进再就业为目的,提出失业保险金与给付期限的调整方向,很少将经济周期纳入分析中。失业保险水平的提高(包括失业保险金的提高与给付期限的延长)会对再就业产生两种方向相反的影响,即在失业者的基本生活得到保证后产生的促进再就业的收入效应和抑制再就业的替代效应。王元月和马驰骋[7]利用Cox 比例风险模型进行研究,结果表明在失业保险金不变时,给付期限与失业时间呈同向变动关系。杜凤莲和刘文忻[8]、马驰骋等[9]的分析证实了提高失业保险金水平对再就业具有负向激励作用。与此不同,梁斌和冀慧[10]利用“中国家庭金融调查”与“中国时间利用调查”数据考察了失业保险金变动对失业者求职努力程度的影响,并展示了失业保险在促进再就业方面的显著效果。邬思婷[11]基于工作搜寻理论发现,失业保险制度对农民合同制工人失业后的生活起到了一定的保障作用,有利于其再就业。而孙守纪等[12]使用Cox比例风险模型的实证分析表明,失业保险在城镇职工中存在着显著的再就业促进效应,但在迁移工人中存在着显著的再就业抑制效应。可见,使用不同调查数据和实证方法对两种效应的综合作用进行衡量会得出不同结论。国内也有少数学者考虑了经济周期因素,认为发挥失业保险的逆周期调节作用在中国尤为重要[13-15]。
综上所述,国外文献关于失业保险金最优调整方式的研究结果表明,不同国家所适用的调整方式可能不同。国内研究则很少将经济周期因素加入失业保险给付制度设计中。本文的边际贡献体现在以下两个方面。首先,本文将经济周期波动加入到最优失业保险给付模式的分析中;其次,本文通过相关文献分析发现,虽然失业保险金金额提高与给付期限延长都是提高失业保险水平的途径,但是两者带来的再就业影响却有所差异。因此,本文将失业保险给付模式分为失业保险金金额调整和给付期限调整两个方面,并将两者的调整结合起来给出优化策略。文章的安排如下:第三部分介绍理论基础;第四部分使用省级数据进行实证分析以确定失业保险金的最优周期性调整策略;第五部分使用动态均衡法对给付期限的调整进行分析;第六部分进行总结并提出政策建议。
三、理论基础
(一)最优失业保险金模型
1.模型假设
LANDAIS等[2]分别对劳动力、公司以及政府三个主体进行分析,推导出不同经济周期下的最优失业保险金模型。为了简化模型,首先本文将劳动力总数量标准化为1,并假设劳动力为同质化个体。对于处在t时刻的劳动者来说,其效用为ut=u(ct,Nt),ct为消费、Nt为就业。该个体一生的总效用可以表示为式(1),ρt为t时刻的贴现率。在给定失业保险金水平下,个体会以最大化自身期望效用为目标来决定其找工作的努力程度。
其次,同质化的公司将基于自身效用最大化,通过权衡招工成本和新工人带来的生产力收益决定是否提供新岗位。假设公司共有l名职员,其中n人负责提供生产力,即生产函数中的Nt部分。剩余部分员工负责招收新职员,τ(θ)表示人力部门员工数与其余员工数的比值。因此满足等式l=[1+τ(θ)]n,τ'(θ)>0,l'(θ)>0。公司的生产函数为式(2),其中α、β∈(0,1),Zt为生产力水平参数,Kt为资本投入量。假设提供一个新岗位的成本为cv,空缺岗位占比为Vt,则公司获得的总利润为Πt,可用式(3)表示,该利润会平均再分配给所有劳动者。
最后定义政府给予的失业保险金为b,就业者平均工资为w,则失业保险金替代率为T=。在不考虑个体投资的情况下,定义劳动力就业和失业状态下的消费水平差为Δc=c-cu(Δc >0),其中c=Π+w-λ,cu=Π+b。假设t时刻的失业率为Ut,正常情况下就业者比例远大于失业者,因此根据λ·Nt=b·Ut,人均需要缴纳的失业保险费λ远小于保险金b,故有T≈1-。在就业者平均工资不变的情况下,Δc=w-λ-b的变动可以反映失业保险金的反向变动。
2.匹配函数与劳动力市场均衡条件
3.最优失业保险金
(二)最优失业保险给付期限模型
MOYEN 和STÄHLER[6]假定劳动力存在就业、短期失业和长期失业三种状态。短期失业者可以领取政府提供的失业保险金b,占比为。如果该部分个体在一定时间内还未找到工作,超过给付期限后将转向领取金额较低的失业救济bl,占比为,则此时,在最优失业保险金模型中的s可代表个体从就业转为短期失业的概率。定义sl为个体由短期失业转向长期失业的概率,它与政府决定的失业保险给付期限呈负相关关系。sl满足式(6),其中ρl为平滑效应参数,衡量了在经济波动时期sl维持原状的能力,φy表示总产出的波动影响参数,φU表示失业率的波动影响参数。此时,劳动力市场的均衡还可以用式(7)~式(9)来表示。
劳动者的个人投资为It,市场利率为rt,资本折旧率为δ,平均再分配总利润为Πt。基于个体收支平衡原则得到预算约束式(10),左端为个体的总支出,右端为总收入。其中tt表示一次性税收支出,Kt满足Kt=()1-δ Kt-1+It。仅关注失业保险,政府的预算约束为式(11)。基于以上框架,第五部分分析了在外生冲击造成的经济波动下,政府如何调整失业保险给付期限才能同时提高就业者和失业者的效用。
四、最优失业保险金调整策略分析
(一)基准参数估计
首先对η、α、∈d、εm四个参数值进行估计。本文使用中国31 个省份2010 年—2016 年的面板数据进行个体固定效应回归得到η的估计值;使用中国1978 年—2019 年的时间序列数据(各指标均以1952 年为基期进行调整)进行二阶自回归OLS估计得到α的估计值④。SHIMER[16]的研究认为,只有找到工作的概率在0.65 以上时人们才会付出时间去寻找工作,且概率的波动导致的求职努力程度变化不明显,最多只会产生4%的变化。因此,为了简化模型可将∈d近似为0。
εm为失业保险金额的变化对失业者再就业的影响程度。短期内劳动力市场紧密程度不变,此时失业保险金的增加会提高失业者维持现有生活水平的能力,从而延长失业持续时间,导致失业率提高。因此短期弹性εm为正值。在保障水平极低或极高时,小幅度调节失业保险对个体寻找工作的决策不会产生很大影响,此时弹性取值较小。只有当保险保障水平恰好处于可以维持正常生活的临界值时,失业保险的调整才会对个体决策产生明显影响。美国失业保险金替代率处于临界水平,而我国失业保险金替代率仅为16%。因此参照LANDAIS等[2]设定美国的εm=0.5,合理假设我国εm=0.25。将表1 中的参数值代入式(5)中,最优失业保险金公式可化简为式(12)。

表1 参数估计值
此时,式(12)中的未知参数仅剩失业率对失业保险金变动的长期弹性与短期弹性的比值,令合理地假设k值的取值范围为k∈[-3,1]。根据式(12)选取不同的k值,做出1-随的变化图,见图2(0 ≤1-)。图2 横轴为经济周期的衡量变量,与经济形势呈正相关关系;纵轴1-表示最优失业保险金替代率,与失业保险金水平同向变动。从图中可以看出,最优失业保险金的调整方向与k值的符号有关。当k>0 时,随着经济下行,失业保险金应该向上调整,即采取逆周期调节方式;相反当k<0时,失业保险金应采取顺周期调节方式。
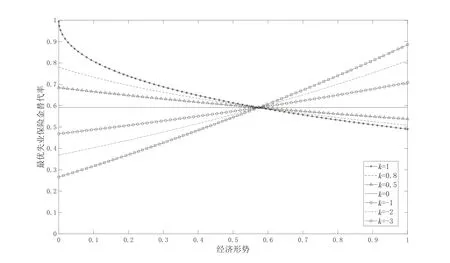
图2 最优失业保险金替代率随经济波动变化趋势图
(二)k值测算
k值的符号取决于短期内就业人员工资以及税收水平不变时,Δc的变化(失业保险金水平的反向变化)对市场紧密程度的影响。根据表2 的分析,本文通过对值的测算来估计k值符号,即估测失业保险金关于劳动力市场紧密程度弹性的符号。

表2 k值分析表
本文选取了中国30 个省份2010 年—2021 年共360 个数据进行值的实证分析⑤。被解释变量为劳动力市场紧密程度,由公共就业服务统计中登记招聘人数与求职人数之比表示。主要解释变量为失业保险金。根据奥肯定律提出的经济增长与失业率之间的关系以及菲利普斯曲线阐述的失业率与通货膨胀之间的联系,本文选取了地区名义生产总值指数和地区居民消费价格指数作为控制变量。此外,城镇就业人员结构、失业保险领取率和失业保险覆盖水平也会对市场紧密程度产生影响。城镇就业人员结构衡量了劳动力市场的流动性,使用国有单位就业人数占城镇非私营单位就业人数的比例衡量。失业保险领取率衡量了失业保险金领取的难易程度,定义为年末失业保险金领取人数与该年度参保人数之比。失业保险覆盖水平用失业保险参保人数与就业人数之比表示。对变量的描述性统计如表3所示。
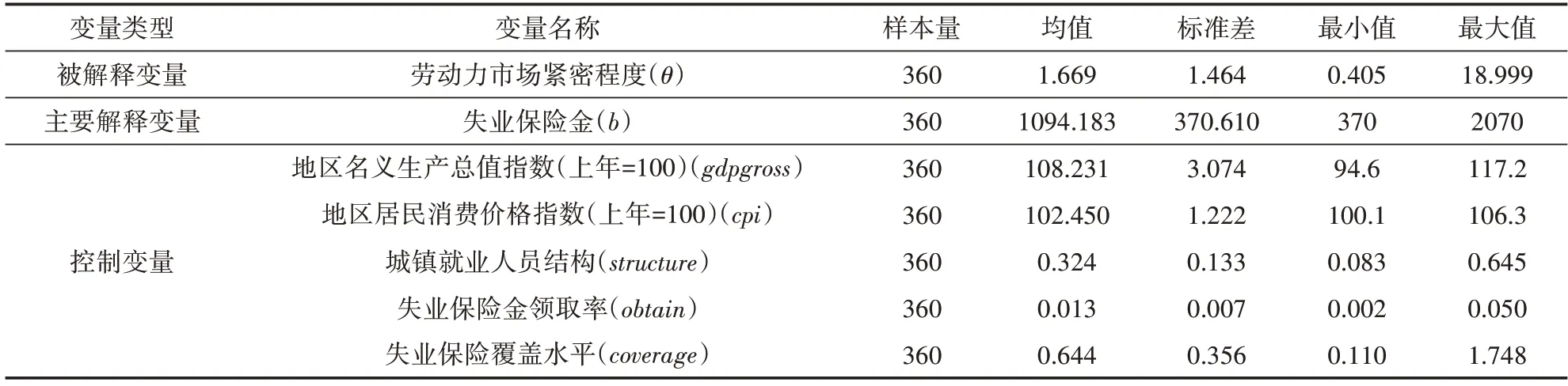
表3 变量描述性统计
1.基准回归
首先进行回归模型的选择。固定效应回归中输出的F 检验结果表明,固定效应回归明显优于混合回归。同时,对年份虚拟变量的F 检验不能拒绝“不存在时间效应”的原假设。因此,此处仅考虑个体效应,不考虑时间效应。个体效应的存在形式有随机效应和固定效应两种,通常使用Hausman检验进行选择。但是当存在异方差和序列相关时该检验会失效。表4 中的检验结果表明,模型存在组间异方差和组内自相关现象。因此选择使用基于过度识别检验的Wald统计量进行随机效应和固定效应的选择。该结果在1%的显著性水平下拒绝了原假设,表明固定效应优于随机效应。本文最终使用个体固定效应模型,并对模型进行最小二乘虚拟变量回归(LSDV)。由于存在组间异方差和组内自相关,在进行LSDV 回归时使用了聚类异方差稳健的标准误。同时,为了便于对的直观估计,对市场紧密程度与失业保险金进行了对数化处理。回归模型为式(13),μi为省际固定效应。
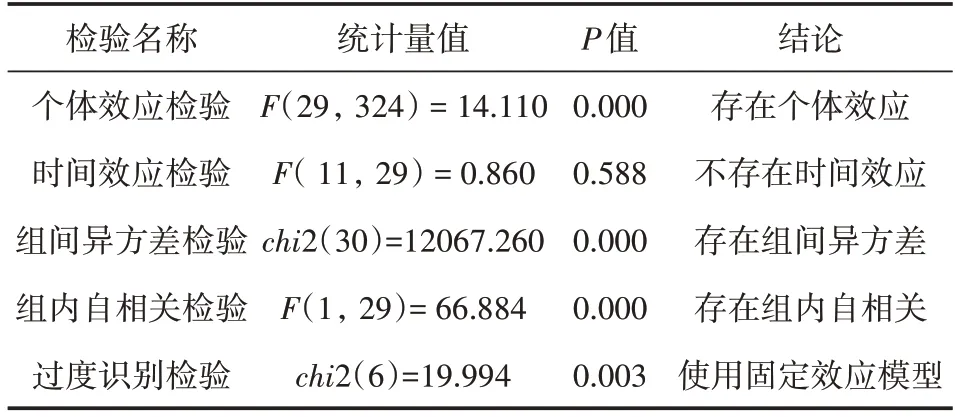
表4 各类基础检验结果
基准回归结果见表5。随着控制变量的不断加入,失业保险金的系数一直显著为正,且大小保持在0.5左右,说明在其他变量保持不变时,失业保险金水平每提高1%会使劳动力市场紧密程度提高0.5%。虽然我国的失业保险替代率水平较低,使得基于小基数失业保险金的变动不会对市场紧密程度产生很大影响,但是回归分析的结果证实了失业保险金提高在提高市场紧密程度方面的正向作用。同时,基准回归的结果与奥肯定律以及菲利普斯曲线所描述的情形一致。经济的增长会刺激就业,从而正向影响劳动力市场紧密程度。失业与通货膨胀之间也的确存在着一种交替关系。当通货膨胀率提高时,失业率下降,劳动力市场紧密程度提高。失业保险覆盖水平的提高也会使市场紧密程度得到提高,其作用原理和失业保险金的增加相同。
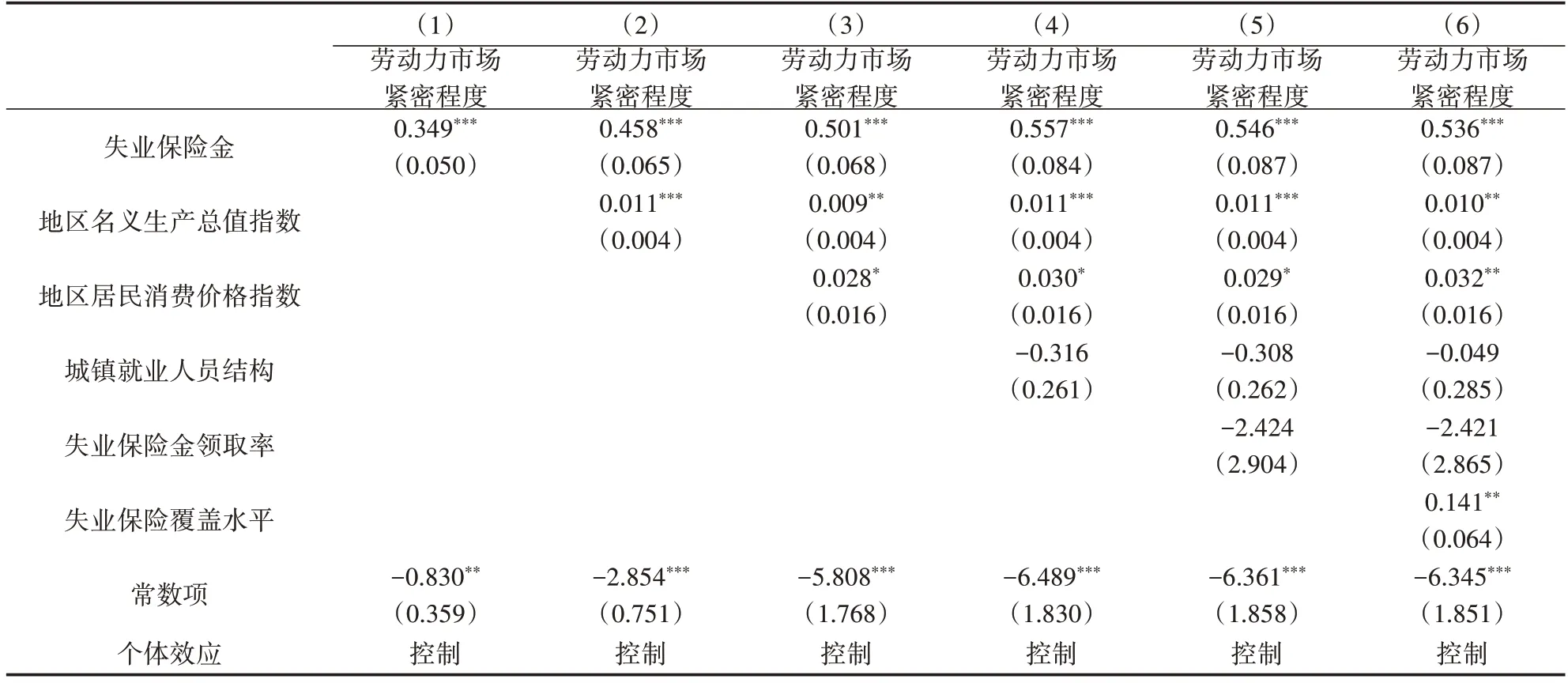
表5 失业保险金对劳动力市场紧密程度的个体固定效应回归
2.稳健性检验
当存在组间异方差与组内自相关问题时,除了可以使用可行广义最小二乘法(FGLS)进行估计,还可以使用面板校正标准误法(PCSE)进行回归。表6 展示的PCSE 回归结果较为稳健,失业保险金对于劳动力市场紧密程度的影响仍然显著为正。地区名义生产总值指数、地区居民消费价格指数等控制变量对市场紧密程度的影响也与LSDV 的回归结果保持一致。
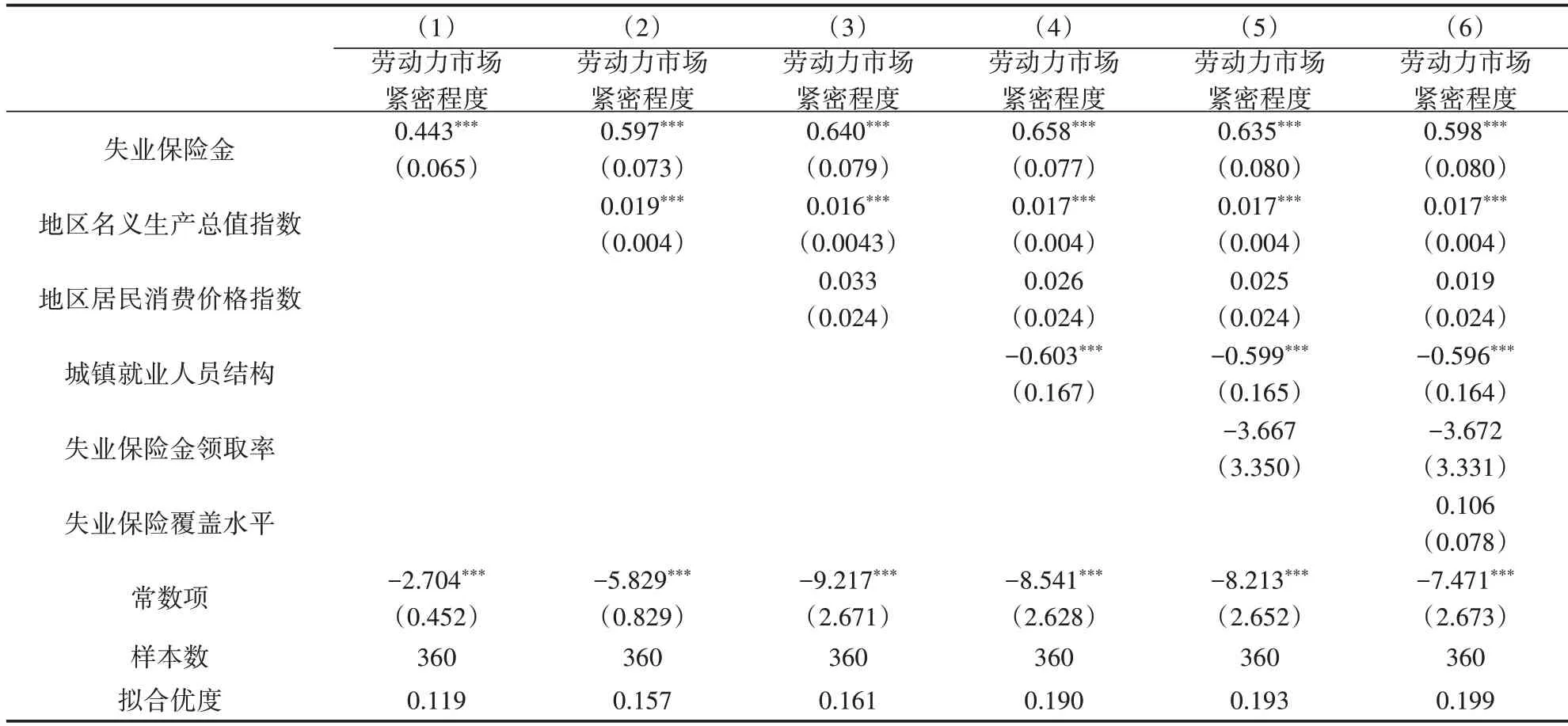
表6 稳健性检验——使用PCSE标准误
五、失业保险给付期限调整策略分析
依据第三部分的理论框架,本文首先分析社会总产出Yt下降10%对劳动力市场的影响。根据式(3)可知,当产出下降时,公司会为了实现利润提供更少的工作岗位。同时,生产规模下降带来的资本需求下降将导致市场利率rt下降。由于工作岗位Vt减少,每单位时间内的匹配的岗位数Mt=ptUt=qtVt随之下降。Ut不变的情况下失业者找到工作的概率pt随之降低。根据式(7)~式(9)可得N2<N1,U2>U1。在生产力持续保持低位的情况下,合理假设sl>s,即短期失业人员增长速率小于长期失业人员增长速率。该变化如图3 中(1)状态到(2)状态所示。
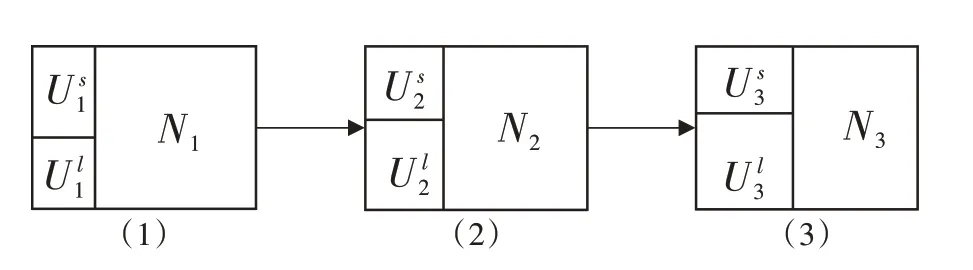
图3 劳动力市场动态变化示意图
其次分析政府在社会总产出下降时延长失业保险给付期限的影响。我国社会保障体系中不存在失业救济,所以bl=0。由于失业保险给付期限的延长,处于短期失业的个体占比增加,sl将降低,可以领取失业保险金的人员占比增加,失业人员人均收益Us·b∕()Us+Ul增加。根据式(11)可得,税收水平将升高。MOYEN 和STÄHLER[6]假定工资是由劳动者与企业间的纳什均衡决定的,则税率的上涨会使就业人员的税前工资增加,使公司经营成本更高。如果此时政府不提供专项政策补贴这项成本,公司将更偏向于不提供新岗位,导致失业率进一步升高。这一变化过程如图3 中(2)状态到(3)状态所示,N进一步减小,总失业率U进一步升高,且w3>w2。根据以上分析,延长失业保险给付期限会造成失业人员占比更高,即U3>U2,但失业人员人均福利上升(仍低于就业者工资w3),就业者工资水平也有所上升,整体人均消费c3与c2的大小关系无法确定。
无论是从以上视角分析还是从道德风险的角度分析,延长失业保险给付期限导致失业率升高都是必然结果。然而,从社会福利的角度来看,该项政策最终能否做到福利的提高,短期内仍需要考察u(c2,N2)和u(c3,N3)的大小,即c3与c2的大小。另外,在Yt逐渐回升至正常水平时期,劳动力市场各指标的变动方向与以上分析相反。此时缩短给付期限,失业人员人均收益减少,相应的税率降低会使得公司岗位成本降低,进一步降低失业率,但纳什均衡下的人均工资水平稍有下降。
综上所述,在经济下行时期,需要综合考虑延长失业保险给付期限带来的失业者福利的提高效应和因此导致的失业率上升带来的本应就业的失业者福利下降效应的大小。而在经济上行时期,如果考虑缩短失业保险给付期限,则一定会带来失业率的进一步降低。
六、结论与政策建议
(一)研究结论
本文在LANDAIS 等[2]构建的最优失业保险金模型与MOYEN 和STÄHLER[6]构建的最优失业保险给付期限模型的基础上,使用中国不同时间段的数据进行最优失业保险给付模式的探究。研究结果表明,首先,中国失业保险金的调整应该采取逆周期方式。当外部的不利冲击导致出现经济增长缓慢、失业率上升等问题时,政府应当提高失业保险金水平,但提高的幅度不应过大,以避免对失业人员再就业造成负面影响。而当经济过热时,可以适当下调失业保险金水平以促进就业。但总体来看,这些调控政策作为经济波动的熨烫器,仅适用于短期的宏观调控。从提高整体社会福利水平的角度来看,我国的失业保险金替代率水平还有很大的提升空间。其次,失业保险给付期限的调整与失业保险金额的调整策略略有不同。在经济下行时延长给付期限,虽然会提高失业保险领取人的福利,但是会引起失业率的进一步上升。因此,应充分考虑两种效应的综合作用进行给付期限的调整。在经济上行时期,可以考虑缩短给付期限以促进失业人员再就业。
(二)政策建议
总体来说,我国失业保险给付模式应遵循逆周期调节的原则。不过考虑到给付期限延长所带来影响的不确定性,在实际操作时,可以将失业保险金和给付期限的调整灵活地结合在一起,以达到社会福利最大化的效果。在经济下行时,可以在提高失业保险金水平的基础上适当地缩短给付期限或者维持给付期限不变。经济下行时,公司由于生产经营状况不佳不会提供大量岗位,所以失业者的寻职成本较高。失业保险金水平的提高正好可以降低失业者的寻职成本,同时给付期限的缩短也会刺激失业者加大其寻职努力程度。这样既可以保证失业保险领取者福利的提高,又可以避免失业率的进一步上升。而在经济上行时,则可以考虑降低失业保险金水平并缩短给付期限。一方面,在经济上行时期,失业者的寻职成本较低。此时,失业保险金水平不宜继续提高,应该和给付期限一起降低,从而促进失业者主动由失业状态转为就业状态,从本质上提高自身福利水平。另一方面,失业保险金水平的下降和给付期限的缩短也可以减少失业保险参与者所缴纳的保险费,从而提高就业者的福利。
[注 释]
①我国的第一部《失业保险条例》经1998 年12月16日国务院第11次常务会议通过,由国务院于1999 年1月22日发布并实施。
②数据来源于《2022 年度人力资源和社会保障事业发展统计公报》。
③数据来源于国家统计局官网和《中国劳动统计年鉴》。
④该回归结果在此处由于篇幅问题不予列出,感兴趣可联系作者查看。
⑤数据来源于《中国劳动统计年鉴》,各地区人力资源和社会保障部官网和国家统计局官网。
