基于尺度自适应CoF的红外与可见光图像融合算法研究

焦登辉，刘文波，刘伟峰，曹晓倩

(陕西科技大学 电气与控制工程学院，陕西 西安 710021)

0 引言

图像融合是信息融合领域的重要分支之一，其在国防军事[1]、城市交通[2]、医疗[3,4]、工业[5]、摄影等领域中得到了广泛的应用.其中，红外和可见图像融合作为一种可靠的侦察工具，在国防军事领域有迫切的应用需求.

红外传感器可以不受光照条件影响，在雨、雾、粉尘等恶劣环境条件下正常工作，但所得图像存在空间分辨率低、细节差、纹理缺失等明显缺点.相应地，可见光图像具有较高的空间分辨率和丰富的纹理细节，符合人类视觉感知.然而，可见光传感器在恶劣环境条件下成像效果显著下降.可见光图像和红外图像融合的关键是对二者间存在的互补信息相结合生成拥有高质量的细节融合图像，以助于实现对特定目标的全天候精准识别和监控.

根据现有研究成果，红外与可见光图像融合可以在像素层、特征层以及决策层三个不同层系进行.其中，像素层中的多尺度分析融合算法一直是最为活跃的算法，也被诸多研究学者进行改进和创新，如拉普拉斯金字塔(Laplacian Pyramid,LAP)[6]、离散小波变换(Discrete Wavelet Transform,DWT)[7,8]、曲线变换(Curvelet Transform,CVT)[9,10]和非下采样轮廓变换(Nonsubsampled Contour Transform,NSCT)[11]以及非下采样剪切波变换(Non-subsampled Shearlet Transform,NSST)[12]等.但是，红外和可见光图像在传统多尺度域融合规则下普遍存在容易损失图像边缘信息的问题，因此边缘保持滤波器便被作为图像预处理步骤被广泛应用到图像融合领域中.

目前，常用的边缘保持滤波算法主要包括双边滤波算法(Bilateral Filtering,BF)[13]、基于L0的梯度最小化算法(L0 gradient minimization,L0)[14]、双边纹理滤波算法(Bilateral texture filtering,BTF)[15]、相对总变异算法(Relative Total Variation,RTV)[16]、引导图像滤波(Guided Image Filter,GIF)[17]等.这些算法具有较好保留图像轮廓边缘信息的能力，并且能有效减少融合结果中边缘周围的光晕伪影,但这类算法均通过强度相似性和位置邻近程度对每个领域像素分配权重，根据权重的大小决定是否进行平滑操作以达到保留边缘的效果.但是纹理通常具有很高的相似性和相似的局部统计性，它们并不能区分纹理区域内的边缘和各纹理区域之间的边界，导致算法在应用中会将纹理细节与边缘同时平滑.为了解决这类问题，Jevnisek等[18]在2017年提出了共现滤波(Co-occurrence Filter,CoF)算法，该滤波器利用图像本身的共现信息[19]分配权重值，从而调整平滑程度，完成对纹理细节与边缘区域的区分.但是对于一些梯度较大且出现频率较高的边缘CoF会将其误认为纹理而对其进行平滑，影响对图像边缘信息的保留.

针对这一问题，本文提出一种基于梯度值变化的尺度自适应CoF，并将其与典型的多尺度域融合算法NSST相结合实现红外与可将光图像融合.目的是为了在保留结构，平滑纹理的基础上对图像中梯度值变化较为明显的、出现频率较高的边缘进行保留，提高融合图像的被认知和理解能力.

1 尺度自适应CoF

1.1 共现滤波器(CoF)

CoF是一个局部线性滤波器，其定义如下：

(1)

式(1)中：p和q为像素索引，且q为p的领域像素；Yp为输出图像的像素值；Xq为输入图像中像素p的领域像素q的像素值；ω(p,q)为邻域像素对目标像素贡献的权重.ω(p,q)表示为：

ω(p,q)=Gδs(p,q)·M(XP,Xq)

(2)

式(2)中：Gδs表示高斯滤波器定义为

(3)

式(3)中：d(p,q)表示像素p与像素q的欧几里得距离；δs是指定参数.

M是归一化共现矩阵，定义为：

(4)

式(4)中：C(a,b)是图像的共现矩阵，h(a)表示灰度值为a的像素点出现的频率，h(b)同理.对于一般灰度等级是0-255的灰度图像来说，归一化共现矩阵M(a,b)为256×256矩阵.C(a,b)表示为：

(5)

式(5)中：δ是高斯滤波参数；[*]表示如果命题*表示为真，则[*]=1，否则为0.

针对图1(a)所示棋盘格图像，采用原始CoF滤波器进行滤波，输出图像如图1(b)所示.由图中明显可见，棋盘格的内部纹理被严重模糊.其实这一点也是可以预见的：原始CoF通过像素点对之间的共现信息调整平滑的权重，而共现信息只与其图像像素点对之间的灰度值、距离以及灰度值出现的频率有关，这将直接导致图像中出现频率高且距离较近的细小边缘被平滑，正如图1(a)中的棋盘边缘被模糊.

图1 原始CoF与尺度自适应CoF的滤波结果

1.2 改进的尺度自适应共现滤波器

针对原始CoF存在上述容易模糊出现频率高且距离较近的细小边缘的问题，本文将图像梯度引入算法中，利用梯度值大小自适应调整滤波尺度，在保留CoF对背景平滑能力的基础上，实现对细小边缘的保留.

1.2.1 归一化梯度

由于不同图像的梯度值范围各不相同，故采取归一化梯度的方式以便后续对自适应滤波尺度的计算.

采用3*3窗口的标准sobel算子计算各像素点的梯度值：

(6)

gx=f(k+1,l-1)+2f(k+1,l)+f(k+1,l+1)-

f(k-1,l-1)-2f(k-1,l)-f(k-1,l+1)

(7)

gy=f(k-1,l+1)+2f(k,l+1)+f(k+1,l+1)-

f(k-1,l-1)-2f(k,l-1)-f(k+1,l-1)

(8)

式(6)～(8)中：k=1,2,…,K；l=1,2,…,L；(K,L)表示图像的宽与高；g(k,l)为图像(k,l)位置点的梯度值.

梯度归一变换：

G(k,l)=g(k,l)/gM

(9)

式(9)中：gM是图像中最大的梯度值.

1.2.2 自适应滤波尺度及尺度自适应CoF

利用归一化后的梯度值G进行非线性变换，得到自适应的滤波尺度为：

(10)

式(10)中：v为最大滤波尺度；u为最小滤波尺度；c为常数，在本文实验中固定为0.2.

利用自适应滤波尺度代替原始CoF中的固定滤波尺度，使之能够随着图像梯度值的变化而自适应的调整滤波尺度大小，也就是将原始CoF中的δs用δg代替，形成新的高斯滤波器：.

(11)

故尺度自适应CoF定义为：

(12)

图1(c)为图1(a)所示棋盘格图像经尺度自适应CoF滤波后的图像.对比图1(b)可见，经尺度自适应CoF滤波后，虽然对原始图像进行了一定的平滑，但棋盘特性依然清晰可见，大部分的细小边缘得到保留.

2 基于尺度自适应CoF的NSST融合框架

将提出的尺度自适应CoF作为预处理步骤，与传统多尺度域下红外与可见光图像融合算法相结合，有望提升融合算法的边缘保持能力，增强融合图像的可感知和可理解力.

基于NSST的红外与可见光的融合算法具备多分辨率性及平移不变性，能够克服图像边缘处的伪吉布斯现象等优越性能，是传统多尺度域下红外与可见光图像融合算法的典型代表.因此本文使用尺度自适应CoF与NSST相结合的方式对红外与可见光图像进行融合，整体融合框架如图2所示.

图2 尺度自适应CoF+NSST图像融合框架

首先，利用尺度自适应CoF对红外图像与可见光图像进行滤波，目的是为了尽可能保留源图像的边缘信息，以免后续操作造成的边缘丢失的情况.其次使用NSST算法对滤波后的图像进行高低频分解，然后利用不同的融合算法分别对高低频子带进行局部融合，最后使用NSST算法进行逆变换得到全局融合图像.

图3为尺度自适应CoF+NSST图像融合算法结果示意图.图3(a)和图3(b)分别为输入的原始可见光与红外图像，两者分别经尺度自适应CoF处理后得到图3(c)和图3(d)，然后使用NSST算法对图3(c)和图3(d)进行融合，得到融合后图像图3(e).

图3 尺度自适应CoF+NSST图像融合算法效果图

3 仿真实验及结果分析

本文仿真实验分为两个部分，第一部分是尺度自适应CoF的滤波性能评估实验，第二部分是尺度自适应CoF对NSST图像融合算法有效性的评估实验.

实验环境配置为：Intel(R)Core(TM)i5-10500 CPU @3.10 GHz 3.10 GHz的处理器，内存为32GB，Windows64位的操作系统，仿真软件为Matlab R2018a.并且此实验中的红外和可见光图像来自公开的TNO图像融合数据集，本文选取了其中两组图像.

3.1 尺度自适应CoF的滤波性能仿真结果及分析

本小节验证尺度自适应CoF对边缘保持方面有效性.为了评估其有效性，选择了L0以及RTV两种经典的算法作为对照算法.

本文实验中需要设置两个参数滤波最大尺度v与滤波最小尺度u.当梯度值较小时最大滤波尺度发挥平滑图像的作用，当梯度值较大时最小滤波尺度发挥保留纹理的作用，在本文中v值取4，u值取0.5.

实验结果如图4所示，图4(a)～(e)分别是原始输入图像、L0算法滤波结果、RTV算法滤波结果、原始CoF滤波结果及尺度自适应CoF滤波结果；从左至右分别是马赛克花草图像、三条鱼图像.从图4可见，本文提出的尺度自适应CoF在红框中大梯度纹理的保持以及对黄框中图像结构的保持和蓝框中梯度较小的纹理平滑上都优于其他对比算法.

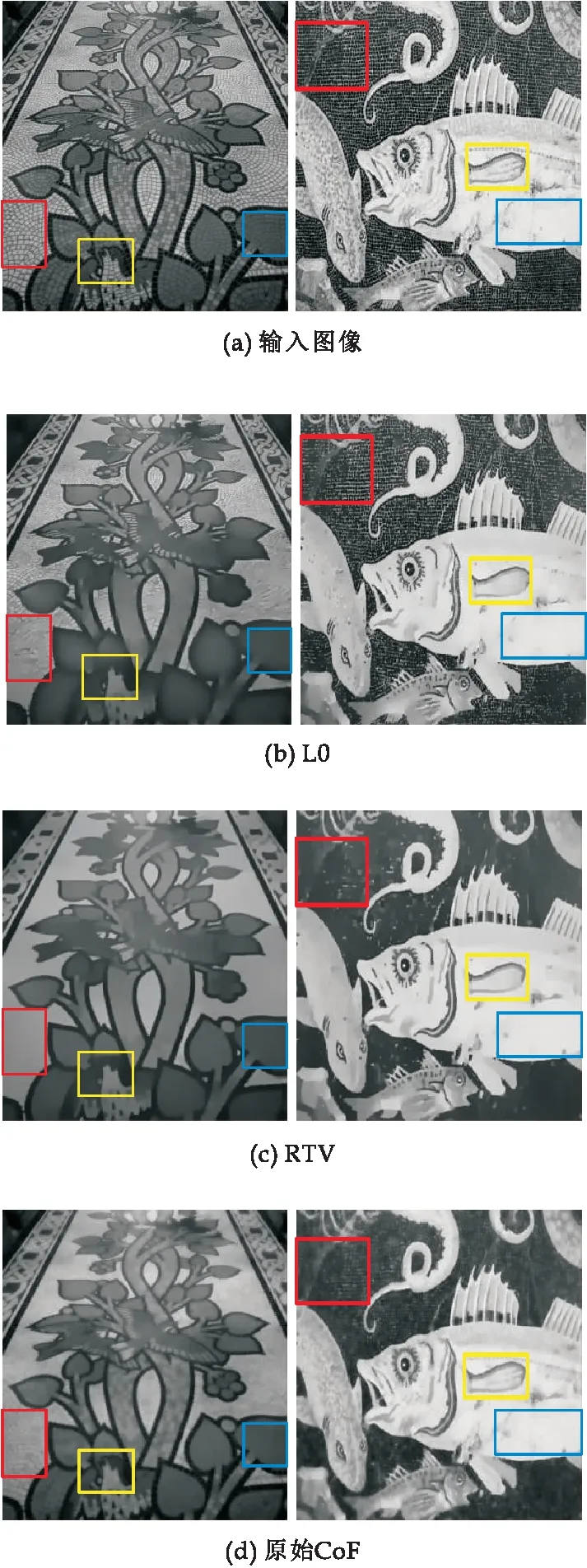
图4 边缘保持滤波算法对比图

3.2 基于尺度自适应CoF的NSST融合算法仿真性能及结果分析

为了验证尺度自适应CoF对NSST图像融合算法边缘保持性能提升的有效性，本小节将原始NSST算法、原始CoF+NSST算法、基于尺度自适应CoF的NSST算法性能进行对比分析.

实验结果如图5所示.图5(a)～(e)分别是输入的可见光图像、输入的红外图像、NSST算法融合结果、基于原始CoF的NSST算法融合结果和本文算法融合结果.从左向右依次为庭院中的人图像和户外中的人图像.

对比图5(c)、图5(d)与图5(e)可知，图5(e)中左图所示的结果对黄框中树枝纹理的保持以及对红框中地面纹理的保持上取得了更好的结果，图5(e)中右图所示的结果完整且清晰的保持了红框中人物轮廓信息，并且对黄框中树枝的纹理信息保持的更完整.总体来说，图5(e)整体轮廓信息较图5(c)和图5(d)更清晰，观感更好.

图5 尺度自适应CoF对NSST图像融合算法有效性对比图

为了客观的评估本文算法性能，本文采用视觉信息保真度融合指标(Visual Information Fidelity for Fusion,VIFF)、峰值信噪比(Peak Signal to Noise Ratio,PSNR)、结构相似性(Structural Similarity,SSIM)三种图像融合常用的评价指标对本文算法的性能进行评估.

其中VIFF是一种基于视觉保真度的多分辨率图像融合质量评价指标，该指标对图像质量的预测有很好的效果；PSNR描述了融合图像与参照图像之间对应像素点的差异，峰值信噪比越大，表明融合图像越理想；SSIM是根据人类视觉感知系统定义的图像质量评估算法，其反映两幅图像之间的结构相似度，值越大表明图像融合效果越好.

针对PSNR、SSIM评价指标，本文分别选取红外图像和可见光图像为参照图像，为了使结果更精准，均使用平均值反映二者与融合图像的综合指标.

表1所示为对图5中左右两组对照图像的客观评价结果，其中加粗的数值为最优值.从表中可以看到本文提出的基于尺度自适应CoF的NSST融合算法较直接使用NSST融合算法和使用基于原始CoF的NSST融合算法在这三项评价指标中取得了比较好的结果.其中本文算法在VIFF评价指标下情况最好，说明本文算法的融合结果与人眼视觉系统感受相近.在PSNR和SSIM的评价指标下也取得了不错的结果，说明本文算法与原图在结构相似度方面也较为接近.

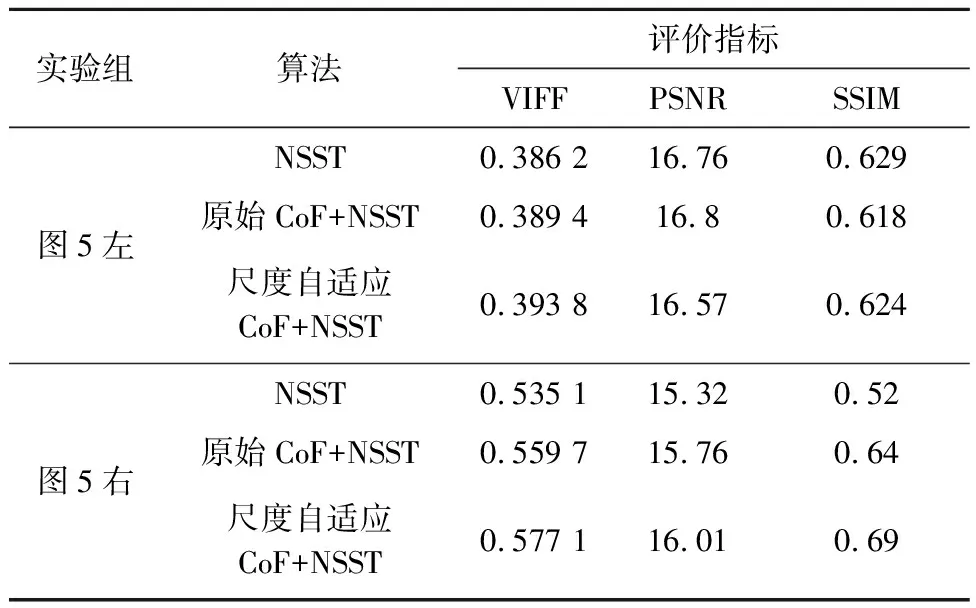
表1 两组对比图的客观评价

4 结论

针对红外和可见光图像在传统多尺度域融合规则下容易损失图像边缘信息的问题，本文提出将一种尺度自适应CoF与NSST相结合的融合框架.这种尺度自适应CoF将图像梯度引入滤波尺度中，然后通过自适应滤波尺度调整平滑力度，在保留原始CoF结构信息保持能力和去噪能力的基础上，保持密集的大梯度边缘信息，增强人们对滤波后图像的理解能力.实验表明：相对于原始的NSST算法、原始CoF+NSST算法，本文提出的尺度自适应CoF+NSST融合框架在边缘保持性能上具有更好的表现，客观评价指标也证明了算法的优越性.