考虑碳减排的多能源系统网格化优化调度方法

2023-03-04金红洋申永山张铁岩王泽镝

可再生能源 2023年2期

金红洋，申永山，滕云，张铁岩，王泽镝

（沈阳工业大学电气工程学院，辽宁沈阳 110870）

0 引言

随着我国能源绿色低碳转型进程的加速，以低碳甚至零碳为目标的多能源系统得到了快速发展[1]～[3]。多能源系统调度运行面临巨大挑战。一方面，具有能量异质性的多能源系统的形成和发展，使能量输运、存储和消费方式都发生了根本性转变；另一方面，具有不确定性的高比例可再生能源并网，使多能源系统调度从传统集中式确定性问题转变为分布式不确定性问题[4]，[5]。为应对上述挑战，多能源系统亟需新的考虑安全性、经济性和环保性等多维需求协同的灵活调度方法。

目前，国内外学者针对多能源系统的优化调度开展了大量研究。文献[6]以多能源系统调节能力提升为目标，提出基于电热氢储能协同的多能源系统优化调度方法，并通过仿真算例，验证了该方法对多能源系统灵活性提升和运行经济性提升的有效性。文献[7]提出了多能源电网集群运行优化方法，能够聚合热电联合响应和可再生能源等分布式资源，提升了多能源系统的功率调节响应能力，并减少了多能源系统的调节成本。文献[8]利用电氢耦合特性，面向无废充能服务区多源微网，提出多能源系统优化运行方法，该方法在保证系统经济性的同时，有效提升了多能源系统的调节能力。文献[9]利用分布式储能的集群优势，提出多能源系统网格化储能协调优化方法，提升了多能源系统新能源消纳水平，降低了多能源系统能量平衡调节成本。以上研究对多能源系统调度过程中面临的不确定性问题和分散性协同问题均给出了较好的解决方法。然而，随着风电、光伏等可再生能源渗透率不断加大，多能源系统不确定性增强，由不确定性导致的调节需求的增加和改变更为明显，传统调度手段难以快速支撑调节需求的增加和改变，如何高效地调整多能源系统运行方式，以应对具有不确定性的复杂调节需求变化，是未来低碳甚至零碳多能源系统优化调度的重点和难点问题。

为此，本文提出一种考虑碳减排的多能源系统网格化优化调度方法。首先，为提升多能源系统调节的灵活性，在研究多能源系统能量平衡模型的基础上，提出了多能源系统调度网格划分方法；然后，为保障系统安全性、经济性和环保性多目标之间的协同，提出了考虑碳减排的多能源系统网格化优化调度模型；最后，进行仿真算例分析，验证本文所提模型的有效性。

1 多能源系统能量平衡模型及网格划分方法

本文研究的多能源系统拓扑结构如图1所示，该系统是由电力系统、热力系统和天然气系统耦合形成的有机整体，包含电能、热能和天然气能的能源生产、转换、分配、存储和消费等环节。

图1 多能源系统拓扑结构Fig.1 MES topology

1.1 多能源系统能量平衡模型

（1）电力系统能量平衡模型

多能源系统中的电力系统网络模型包括可再生能源发电系统、燃气轮机、电锅炉、电制气装置、循环水泵、压缩机、储电装置、电负荷和电力传输线路等。在电力系统网络潮流模型中采用交流潮流模型来表示节点功率平衡，为了提升计算效率，采用直流潮流模型计算电力传输线路功率，并在电功率平衡模型的基础上，增加能源耦合设备功率平衡模型。电力系统能量平衡模型为

式中：P和Q分别为电力网络节点注入有功功率向量和无功功率向量；U.为节点电压向量；Y为节点导纳矩阵；p为电力传输线路功率向量；pMT，pRE，pES，pSW和pLOAD分别为燃气轮机出力、可再生能源出力、储电输出功率、能源耦合设备用电功率和电负荷向量；He为节点功率对电力传输线路的传输分配因子；PMT，i为燃气轮机输出功率；ηMT，e为燃气轮机的发电效率；HG，LHV为天然气的低品位热值；mg，i为燃气轮机的天然气进气量；PWP，i，，ΔPWP，i和PWP，i，max分别为风电实际出力、风电预测出力、风电出力预测误差和风电出力最大值，并且ΔPWP，i呈正态分布，其分布概率密度函数为fWP，i；PPV，i，，ΔPPV，i和PPV，i，max分别为光伏实际出力、光伏预测出力、光伏出力预测误差和光伏出力最大值，并且 ΔPPV，i呈正态分布，其分布概率密度函数为fPV，i。

（2）热力系统能量平衡模型

多能源系统中的热力系统网络模型包括热源、燃气轮机、电锅炉、循环水泵、储热装置、热负荷和传输管道等。热力网络模型采用水力-热力稳态模型，并在此基础上，增加能源耦合设备功率平衡模型。热力系统能量平衡模型为

式中：Ah为热力系统的节点-支路关联矩阵；m为热力传输管道流量；M为节点流入流量；Bh为热力系统的回路矩阵；ΔH为支路压头损失向量；ΔHb为热力传输管道沿程损失；Z为热力传输管道首末两端的位能差；Hpump为支路的水泵扬程；Ph为节点热功率向量；Cw为水的比热容；Ts和Te分别为热力传输管道始端温度和末端温度；Tenv为环境温度；λh为热力传输管道散热系数；Tx为距离热力传输管道始端x处的水温；mout和min分别为流出节点的流量和流入节点的流量；Tout和Tin分别为流出节点的工质温度和流入节点的工质温度；Pin为节点处注入的热功率；mpump为循环水泵输出流量；Ppump为循环水泵的用电功率；ηpump为循环水泵效率；Hpump为循环水泵扬程；PEBH，i为电锅炉热功率；ηEB为电锅炉的热效率；PMTh，i为燃气轮机的输出热功率；ηMTh为燃气轮机的热效率。

（3）天然气系统能量平衡模型

多能源系统中的天然气系统网络模型包括气源、燃气轮机、电制气装置、压缩机、储气装置、气负荷和天然气传输管道等。天然气网络模型采用天然气系统网络稳态流量模型，并增加能源耦合设备功率平衡模型。天然气系统能量平衡模型为

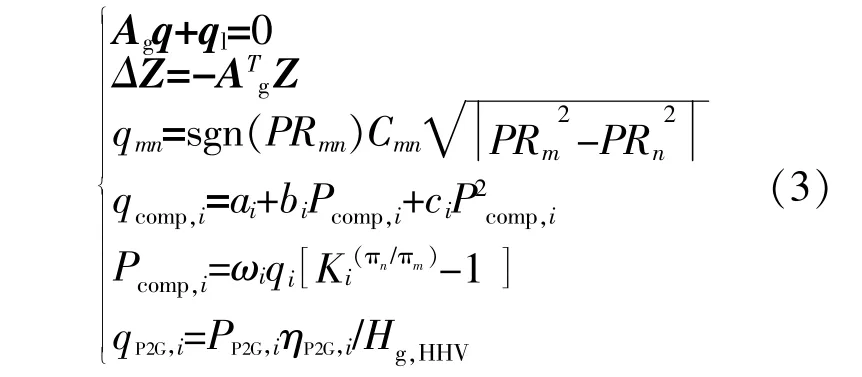
式中：Ag为天然气系统中节点和天然气传输管道的关联矩阵；q为天然气传输管道流量向量；ql为天然气系统中节点净负荷向量；ΔZ为天然气传输管道的压力降向量；qmn为天然气管道mn的流量；PRm，PRn分别为管道两端的压力；Cmn为与管道环境和天然气特性相关的常系数；sgn（PRmn）为方向指示函数，sgn（PRmn）=1表明m端压力大于n端压力，sgn（PRmn）=-1表明m端压力小于n端压力；qcomp，i为压缩机i等效流量；ai，bi，ci分别为压缩机的能源转换效率系数；Pcomp，i为压缩机的用电功率；ωi为压缩机运行温度常数；qi为流经压缩机的天然气的流量；Ki为压缩机加压比；πn和 πm分别为压缩机两端压力值；qP2G，i为电转气输出天然气流量；PP2G，i为电转气的用电功率；ηP2G为电转气的气效率；Hg，HHV为天然气的高品位热值。

1.2 基于能量输运支路传输容量指标的多能源系统网格划分方法

风电和光伏不确定性将导致多能源系统能量供需不平衡，而能量输运支路阻塞是多能源系统在供需不平衡状态下无法发挥多能耦合协调作用的主要影响因素。因此，为提升多区域集群多能源系统网格的调节能力，须要进行调度网格的划分。网格划分具有分解协调的优势，图2为多能源系统网格划分示意图。多能源系统网格划分问题可以转化为以能量输运支路阻塞风险指标作为边权重的无向赋权图的最小割问题。根据多能源系统能量平衡模型，利用图论理论，将多能源系统网络转化为由能量耦合节点和能量输运支路构成的图，多能源系统网络图为

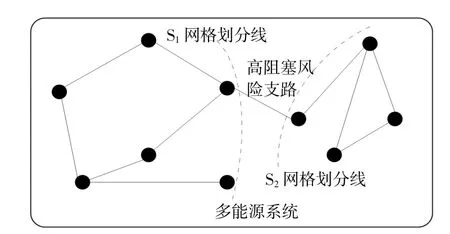
图2 多能源系统网格划分示意图Fig.2 The diagram of MES grid division

式中：Vmes和Emes分别为能量网络节点的点集和能量输运支路的边集；Emes=Ω{p，m，q}，p，m和q分别为电力传输线路功率、热力传输管道流量和天然气传输管道流量；邻接矩阵Ames∈Rn×n，用来表征多能源系统网络Gmes中节点间相邻关系的方阵。

多能源系统网格划分的最小割问题表达式：

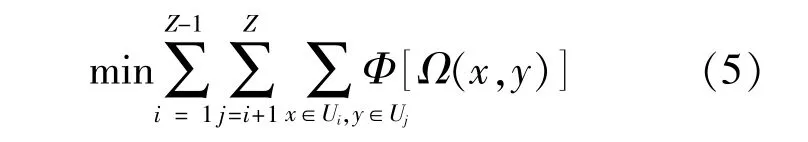
式中：x和y分别为不相交集合Ui和Uj中的节点，割边为 Ω（x，y），并且 Ω（x，y）∈Emes；Z为图Gmes的划分个数，Z取整数并且2≤Z≤；Φ为边权重函数，用能量输运支路阻塞的风险概率计算。

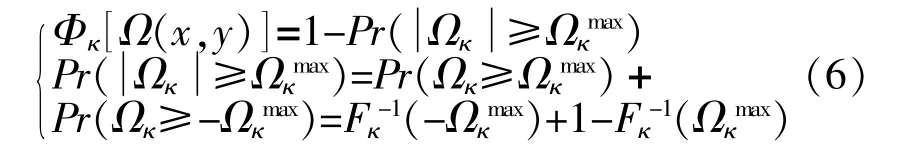
式中：Ωκ为能量输运支路 κ的实际值，包含电力传输线路功率p、热力传输管道流量m和天然气传输管道流量q，Ωκ可根据多能源系统网络模型进行计算；Pr（·）为能量输运支路发生阻塞的概率，可由风电、光伏不确定性的定义以及能量传输分配因子和热能、天然气能关联矩阵的相关公式进行计算；为能量输运支路κ的最大传输容量；Fκ为 Ωκ的累计分布函数，其反函数为。

基于经典图割算法的多能源系统网格划分算法步骤如下：

①初始化多能源系统网络参数，设置迭代次数i=1；

③对图Gmes=（Vmes，Emes）进行任意划分，得到子区域集合S={Si｜i=1，K，}，满足Si∈S和S=Gmes；

④在子区域Si中选取任意节点（x，y），满足（x，y）∈（VSi∩V），利用x和y之间的最小割，将Si划分为和；

⑥更新S={Si｜i=1，K，}，满足∈S，∈S；

⑦end for；

⑨输出基于图割算法的多能源系统网格最优划分结果。

2 考虑碳减排的多能源系统网格化优化调度模型

2.1 目标函数

多能源系统网格化优化调度目标函数应同时考虑多能源系统的运行成本和碳交易成本最小化。

（1）多能源系统运行成本

式中：f1为多能源系统总运行成本；Creg为多能源系统对外部源网的调节成本；Cope为多能源系统的运行成本；，和分别为外购电功率、热功率和天然气功率；，分别为出售电功率、热功率和天然气功率；ce，in，ch，in和cg，in分别为电、热和天然气的单位购能成本；ce，out，ch，out和cg，out分别为参与外部能源网调节的电、热和天然气单位补偿价格；cWP，cPV，cEB，cMT，cpump，ccomp，cP2G，cES，cHS和cGS分别为风电、光伏、电锅炉、燃气轮机、循环水泵、压缩机、电制气、储电、储热和储气的单位时间单位功率运行维护成本。

（2）多能源系统碳交易成本

式中：f2为多能源系统碳交易成本；Ccar_reg为多能源系统与外部能源网络的碳交易成本；Ccar_e为多能源系统内部碳交易成本；ccar_e，in，ccar_h，in，ccar_g，in，ccar_e，out，ccar_h，out和ccar_g，out分别为多能源系统与外部能源网络的碳交易价格；ζe，ζh和 ζg分别为能源联络线路的单位电量碳排放系数；ζMT为燃气轮机的单位电量碳排放系数；Wall（t）为多能源系统在t时刻的碳配额，可根据基准线排放因子法进行确定；ccar为碳交易价格；Wall_H（t）为多能源系统碳排放最高裕度，Wall_H（t）=βWall（t）；ccar_H为碳排放大于碳排放最高裕度时的罚金价格；B（t）为0-1变量，当多能源系统碳排放小于碳排放最高裕度时，B（t）=0，当多能源系统碳排放大于碳排放最高裕度时，B（t）=1。

2.2 约束条件

多能源系统网格化优化调度目标函数的约束条件如下。

除上述约束外，约束条件还应当包括如式（1）～（3）所示的多能源网络约束，并采用凸松弛等线性化技术对多能源网络能量平衡模型中的非线性部分进行转化，此处不再赘述。

3 算例分析

3.1 算例基础数据

本文以中国东北某多能源系统的运行数据和碳排放数据为基础，采用文献[1]建立的改进IEEE 39节点电力系统、14节点热力系统和20节点天然气系统耦合形成的多能源仿真系统进行算例分析。调度周期为24h，步长为1h。采用MATLAB平台编程实现调度模型的仿真，调用CPLEX对调度模型进行求解。

为对比分析多能源网格化优化调度与传统调度的多能源碳减排能力和协调运行能力，设置如下3种场景。场景1：多能源系统不进行网格划分，采用传统优化调度方法，风电容量占比为40%；场景2：多能源系统进行网格划分，采用本文所提方法，风电容量占比为40%；场景3：多能源系统进行网格划分，采用本文所提方法，风电容量占比为60%。设置不同的风电容量占比，是为验证在不同调节需求的前提下，本文所提方法的适用性。

3.2 调度结果分析

表1为场景2和场景3的多能源系统网格划分结果。由表1可知，本文所提算法能够根据系统实际拓扑连接情况以及能量输运支路阻塞风险，对多能源系统进行有效划分。由于风电容量的改变，导致多能源系统网格划分结果出现了差异，原因是风电不确定性风险与能量输运支路阻塞风险的对应关系能够通过能量平衡模型进行量化计算，从而改变能量输运支路阻塞风险指标值，由此得到准确的网格划分结果。图3～5为场景2、场景3采用网格化优化调度方法得到的结果。由图3～5可知，多能源耦合设备能够根据多能源系统的供需关系调整运行状态，如夜间风电功率增加时，电锅炉、电制气等能源耦合单元用电功率也随之增加，为热力系统和天然气系统供能。

图3 场景2、场景3电力平衡曲线Fig.3 Power balance curve of scene2and scene3

表1 多能源系统网格划分结果Table1 The MES meshing results of scene2and scene3

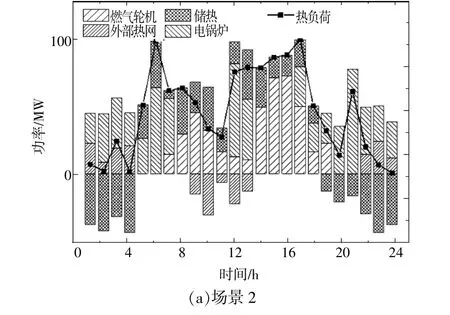
图4 场景2、场景3热力平衡曲线Fig.4 Heat balance curve of scene2and scene3

图5 场景2、场景3天然气平衡曲线Fig.5 Natural gas balance curve of scene2and scene3

表2为3种场景调度对比结果。由表2可知，与传统调度方法相比，本文所提方法能明显降低多能源系统的调度成本，降低碳排放，提高风电、光伏等可再生能源接纳能力。结合调度结果中的弃风率对比以及风光功率曲线，表明场景2、场景3网格化调度比场景1的传统调度的多能源系统的调节能力更强。场景3调度成本和弃风率略高于场景2，这是由于风电容量增加，导致能量传输通道阻塞风险提高，进而导致调度成本和弃风率整体略微增加。