基于Markov-switching GARCH模型的上证50ETF期权定价分析

闫海波,彭凤娇

(新疆财经大学统计与数据科学学院,新疆 乌鲁木齐 830012)

“十四五”规划中提出构建系列期货品种体系,丰富机构投资者种类,推动期货市场和现货市场更加密切联系。在经济快速发展时代,金融衍生品和市场监管体制显得格外重要,金融衍生品的增加对个人、机构甚至是国家都会带来益处,但金融衍生品中的波动率对股票市场会产生不同影响。

波动率的预测和建模有很多方法。1982年Engle[1]提出自回归条件异方差模型(ARCH模型)以解决方差恒定所产生的问题,但在实际应用中会出现自由的滞后分布，故1986年Bollerslev[2]在ARCH模型的基础上提出了广义自回归条件异方差模型(GARCH模型),此模型的优点在于能获取滞后信息,很大程度上解决滞后效应。从此国内外许多学者将GARCH模型与Black-Scholes期权定价模型(BS模型)结合起来开展相关研究。Black-Scholes期权定价模型[3]的提出使得金融衍生工具得到扩展,从而国际金融市场更富有效率。以期货股票市场为研究对象,将GARCH模型运用到BS模型中的文献有:瞿慧等[4-5]使用高频收盘价格建立GARCH模型,同时区分连续波动和跳跃波动,多重考虑跳跃波动和高频数据能获得最佳期权定价;周亮[6]利用动态条件相关自回归条件异方差模型(DCC-GARCH模型)计算各类股票行业指数,利用协方差矩阵的预测能力进行投资组合的动态变化,结果是协方差预测效果要比最小化方差风险预测好;郑尊信等[7]将含跳跃过程的模型运用进BS模型中,最后从多个方面论证了上证50ETF杠杆效应不显著;方艳等[8]利用蒙特卡罗模拟方式计算参数,证明方差无穷自回归条件异方差模型(IGARCH模型)比GARCH模型能更好地拟合波动率;张启文等[9]将中国平安股票数据应用GARCH模型预测的波动率和股票分红去修正BS模型,得到修正的BS模型具有实用价值;Liu等[10]将GARCH模型应用到BS模型的换手率应用到上市公司的股权激励,结果显示的换手率优于GARCH模型的换手率。在国内，对于GARCH模型对市场风险的影响也采取了不同的研究方法。张昱城等[11]利用GARCH模型和在尾部运用极值理论探究尾部风险影响,将斜率变点理论引入传统阈值,结果是产生的尾部风险与流动性风险呈现反比;杨蓦等[12]利用连接函数(Copula函数)和误差修正自回归条件异方差模型(ECM-GARCH模型)对3类农产品进行了套期研究,结果显示大豆产品更能体现该模型的优势,从而降低了市场的价格风险。

但是波动率中有不同的趋势,用GARCH模型提取的波动率中存在时滞效应,进而会区分不同状态,在不同波动情形下解决方案不同。对于不同状态,Stephen[13]提出马尔可夫结构转换GARCH模型(MS-GARCH模型)用概率积分消除条件方差对路径的依赖,但是由于积分难以计算而很难推广。Klaassen[14]改进了Gray的方法,给出预测的迭代公式,促使MS-GARCH理论得到快速发展。

国内外学者将理论应用到实证分析中,如Torre-Torres等[15]、Mozumder等[16]运用蒙特卡洛模型估计马尔可夫转换模型进行转换;Yoo等[17]利用跳跃的GARCH模型进行期权定价,结果显示含跳跃模型优于GARCH模型;魏立佳[18]利用MS-GARCH模型在T分布下,运用马尔可夫链蒙特卡洛算法(MCMC法)对该模型进行估计,结果显示MS-GARCH模型的拟合度优于单状态GARCH模型;Xiao[19]运用MS-GARCH、极值理论(EVT)和COPULA函数对中国股市进行研究,结果表明中国股市对东南亚有一定程度的影响;Ding等[20]运用GARCH模型和MS-GARCH模型与BS模型相结合,得到在稳定状态GARCH模型比MS-GARCH模型拟合要好,反之在波动状态下MS-GARCH模型比GARCH模型拟合要好;黄晓芝等[21]基于改进马尔可夫转换的GARCH模型即动态多维的条件修正波动率进而去预测;陈静思等[22]、华仁海等[23]等运用MS-GARCH模型研究了期权市场与现货市场之间的影响;MS-GARCH模型还可运用到石油[24]、人民币汇率[25-26]等中。

综上国内外学者运用MS-GARCH模型分别在石油、人民币汇率等方面展开研究,虽然Ding等[20]也运用MS-GARCH模型,但并没有分成3个状态。故在3种不同状态下进行回测并预测未来的期权价格,判断在不同时间状态下MS-GARCH模型是否优于GARCH模型。

1 模型介绍

1.1 GARCH模型

GARCH模型是对ARCH模型的重要拓展,它比ARCH模型需要更小的滞后阶数,并与ARCH模型有相类似的结构。GARCH模型定义为

yt=μt+εt,

(1)

εt=etσt,et～i.i.N(0,1)

(2)

(3)

其中:p≥0,q≥0,a0>0,ai≥0 (i=1,…,q),βi≥0(i=1,…,p)。

满足上述条件的模型称为GARCH(p,q)模型,而称{εt}服从GARCH(p,q)过程。当p=0时,GARCH(p,q)过程就称为ARCH(q)过程,当p=q=0时,{εt}为白噪声过程。

GARCH(1,1)是最简单的GARCH过程,它的条件方差函数为

(4)

其中:α0>0,α≥0,β≥0,当α+β<1时GARCH(1,1)就是平稳的。

1.2 MS-GARCH模型

(1) Markov-switching GARCH模型设定 假设GARCH模型的参数依赖于一组离散的状态变量St(St=1,2,…,k,代表过程所处的状态)。这一状态变量是不可观测的,状态之间的转移服从马尔可夫链,{St}满足无后效性,即

P(St=j|St-1=i,St-2=k,…)=P(St=

j|St-1=i)=pij。

(5)

对于i,j=1,2,…,k可得转移概率矩阵

(6)

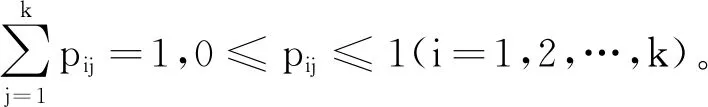
这样,通过转移概率pij,使过程在t时刻所处的状态信息体现在t-1时刻的信息集It-1中。

对于过程{yt}取作

(7)

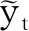
(8)

因此,模型结构变化通过误差项εst来实现,即

(9)

(10)

其中:p≥0,q≥0,a0>0,ai≥0(i=1,…,q),βi≥0(i=1,…,p)。

(2) 似然函数的计算 MS-GARCH-L(1,1)模型的待估参数为

θ=(α0,α1,ε,β1,v,p11,p12,…,pkk,

g1,g2,…,gk)T,

(11)

要进行循环计算。

(3) 基于全样本的平滑概率 “平滑”指在样本内所有观测值的基础上,对于包括t时刻以后的观测值的估计。基于全样本的平滑概率P(St=st|yτ,yτ-1,…,y1)和f(yτ|yτ-1,yτ-2,…,y1)。

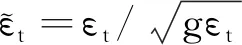
(12)

1.3 BS模型

在二叉树的期权定价模型中,如果标的证券期末价格的可能性无限增多时,其价格的树状结构将无限延伸,从每个结点变化到下一个结点(上涨或下跌)的时间将不断缩短。如果价格随着时间周期的缩短,其调整的幅度也逐渐缩小的话,在极限的情况下,二叉树模型对欧式权证的定价就演变为关于权证定价理论的经典模型——BS模型。

设金融资产价格为随机过程{S(t),t∈[0,T]},该金融资产价格模型为

(13)

则有

(14)

该金融资产的期望与方差为

E[S(t)]=S0eut,

(15)

(16)

欧式看涨期权定价公式为

C=s0N(d1)-Ke-rtN(d2)。

(17)

同理可得,欧式看跌期权定价公式为

P=Ke-rtN(-d2)-s0N(-d1),

(18)

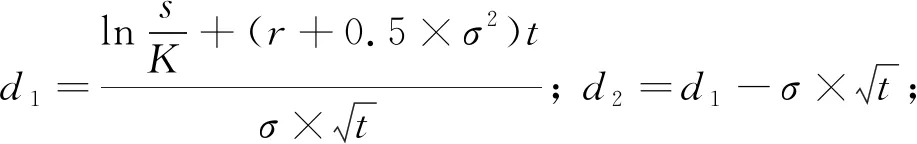
2 实证分析

采用BS模型与GARCH模型和MS-GARCH模型实现对上证50ETF期权定价的实证检验。利用不同模型下和不同状态下的条件方差代入BS模型后观察估计价格和期权价格之间的误差对比。

2.1 统计检验

收集上证50ETF从2015年2月9日到2021年12月31号的收益价进行统计检验，包括正态性检验、平稳性检验、自相关偏自相关检验、异方差检验等。

(1) 描述统计图 上证50ETF从2015—2021年整个收盘价的线性图如图1所示,查看整个收盘价的涨幅情况,同时计算出每日对数收盘率。

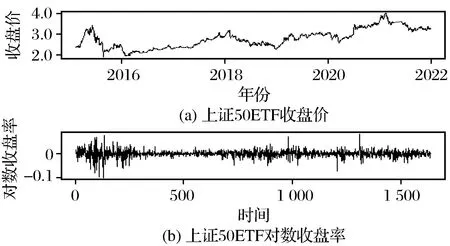
图1 收益序列时序图Fig.1 Revenue series sequence

图1(a)为收盘价在不同年限的涨幅趋势；图1(b)为对数收益率波动情况,在[0,300]、[750,1 200]之间对数收益率波动情况较大,在[500,700]、[1 200,1 500]对数收益率波动情况较小，这种现象称为波动现象且具有连续现象。

对数收益率的描述统计以及概率密度分布见图2。

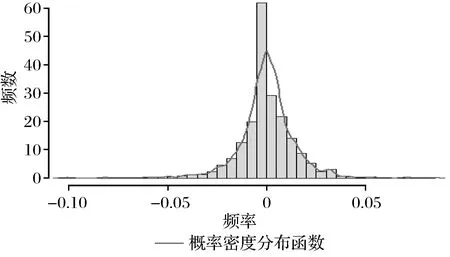
图2 对数收益率序列概率密度分布Fig.2 Probability density distribution of log return series

由图2可见，该分布有明显的尖峰,不是正态分布;通过计算得出对数收益率序列均值为0.000 205,偏度为-0.557 1< 0,峰度为10.197 9>3,比正态分布陡峭,说明对数收益率序列具有尖峰状态。J-B统计量为 3 618.547,P值为 0,拒绝该分布为正态分布的假设,该对数收益率序列具有尖峰厚尾的分布形态。接下来判断数据是否平稳。

采用平稳性检验对对数收益率序列(R)进行ADF单位根检验,带截距项而无趋势项，结果见表1。

表1 对数收益序列单位根检验

由表1可知,在 1%、5%、10% 3种置信水平下,临界值分别为-3.434 1、-2.863 1、-2.567 6,T统计检验值为-40.113 1,小于对应临界值,P值为0,表明上证50ETF对数收益率序列是平稳的。

判断数据平稳后进行对数收益率相关性检验,结果见表2。

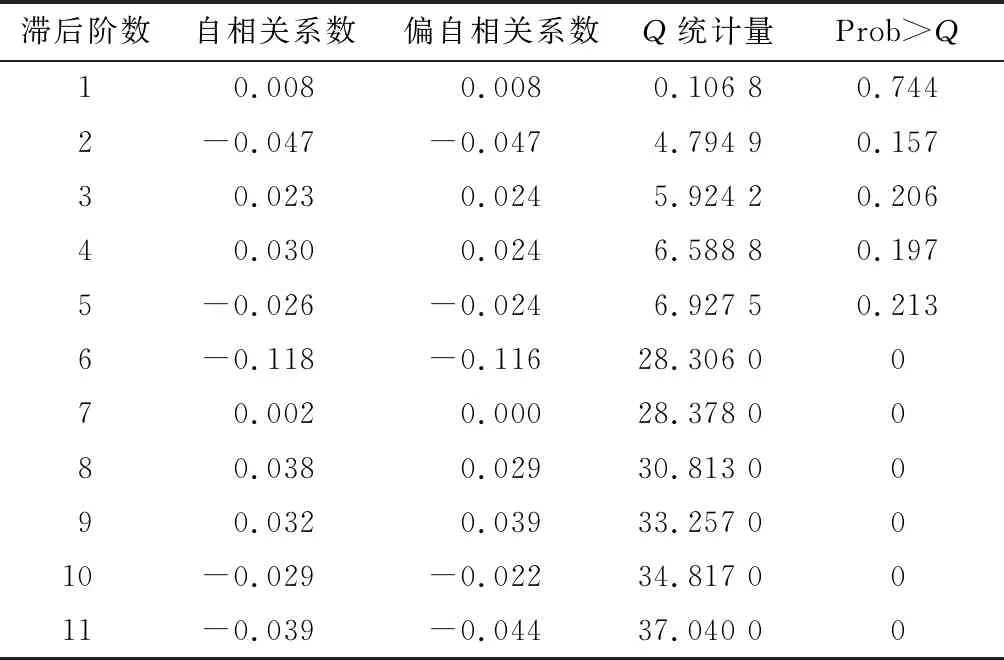
表2 收益率自相关检验

由表2可知,收益率滞后6阶就显著相关,1阶～5阶的自相关和偏自相关的相关系数均落入区间范围内,同时Q统计量的P值统计检验均大于置信度0.05。故序列可能存在相关性,采用ARMA建立模型。因此收益率rt的均值方程为

rt=c+art-p+εt+βθt-q。

(19)

(2) 建立ARMA模型 根据残差滞后阶数,建立ARMA模型,选取不同的P、Q值，结果见表3。

表3 不同ARMA模型下的判断标准

由表3可知，ARMA(1,1)和ARMA(2,2)的各项系数均显著,ARMA(2,2)的AIC系数和SC系数更优于其他模型,所以采取ARMA(2,2)作为均值方程与GARCH模型结合。

(3) 自相关检验、ARCH效应 对数收益率的残差和残差平方相关性检验见图3,判断是否有ARCH效应。

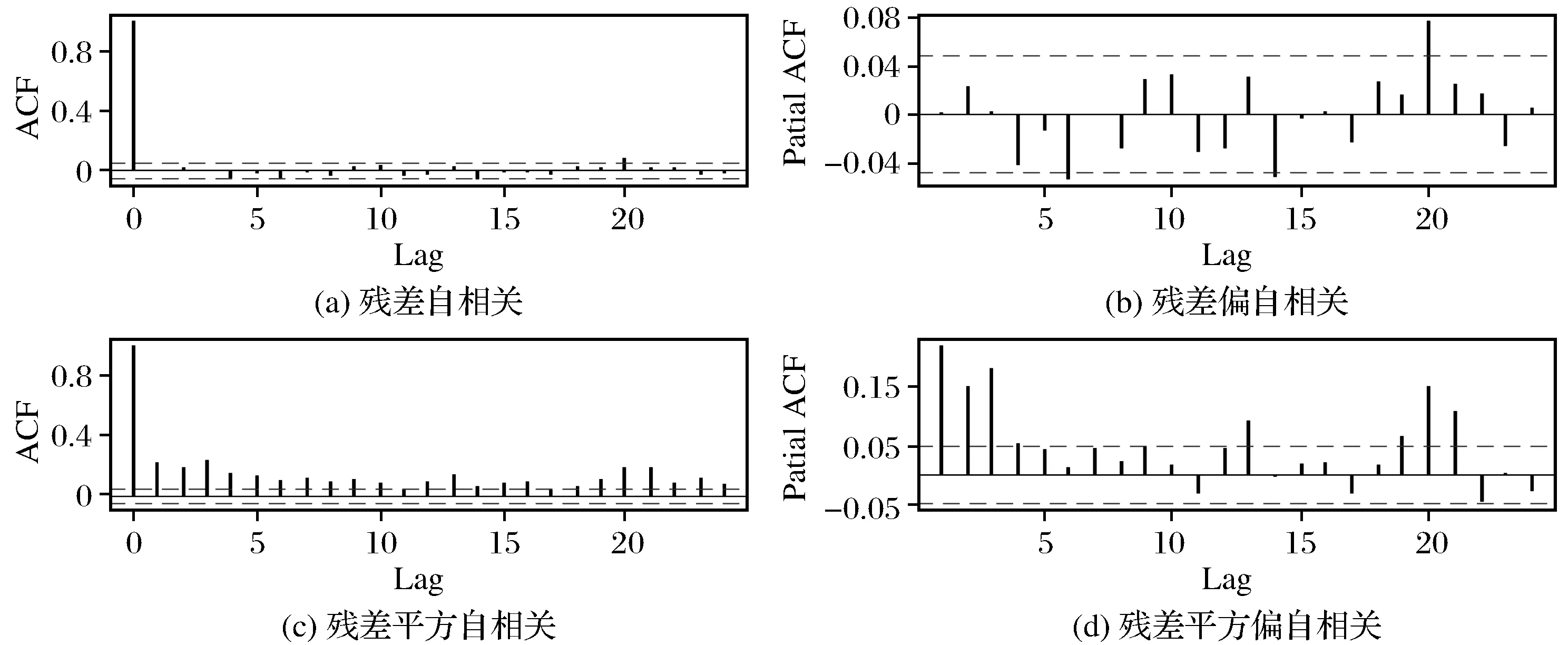
图3 自相关图和偏自相关图Fig.3 Autocorrelation diagram and partial autocorrelation diagram

由图3可知,残差的自相关图(见图3(a))和偏自相关图(见图3(b))的函数值都在置信区间内,即在蓝色的虚线区域范围波动。残差的偏自相关图在6阶、14阶、20阶超出置信水平是种偶然性结果,所以残差序列具有自相关弱相关性,即产生模型为AR(1)。而残差平方的自相关图(见图3(c))却不在置信区间内,故残差平方具有强烈的自相关。

检验对数收益率是否存在ARCH效应,对数收益率的ARCH-LM检验见表4。

由表4可知,F统计量不显著,该序列存在ARCH效应,故建立ARMA-GARCH模型消除ARCH效应。

表4 对数收益率的ARCH-LM检验

2.2 联立方程建模

(1) ARMA-GARCH模型建立 在消除ARCH效应后,通过选择不同的GARCH类型来选择最优模型。ARMA-GARCH(p,q)在不同分布下的AIC和SC值见表5。

表5 ARMA-GARCH(p,q)在不同分布下的AIC和SC值

根据表5可知，TGARCH模型和GARCH模型分别在正态分布和T分布为∂=0.05置信度下系数均显著,根据AIC和SC准则要求越小越好,其中AIC值为-5.995 3,SC值为-5.965 6,故选择ARMA(2,2)-GARCH(1,1)-t模型。

(2) 波动率分析 根据GARCH模型的条件波动率划分状态图(见图4)，根据设定的区间范围画出不同的状态。

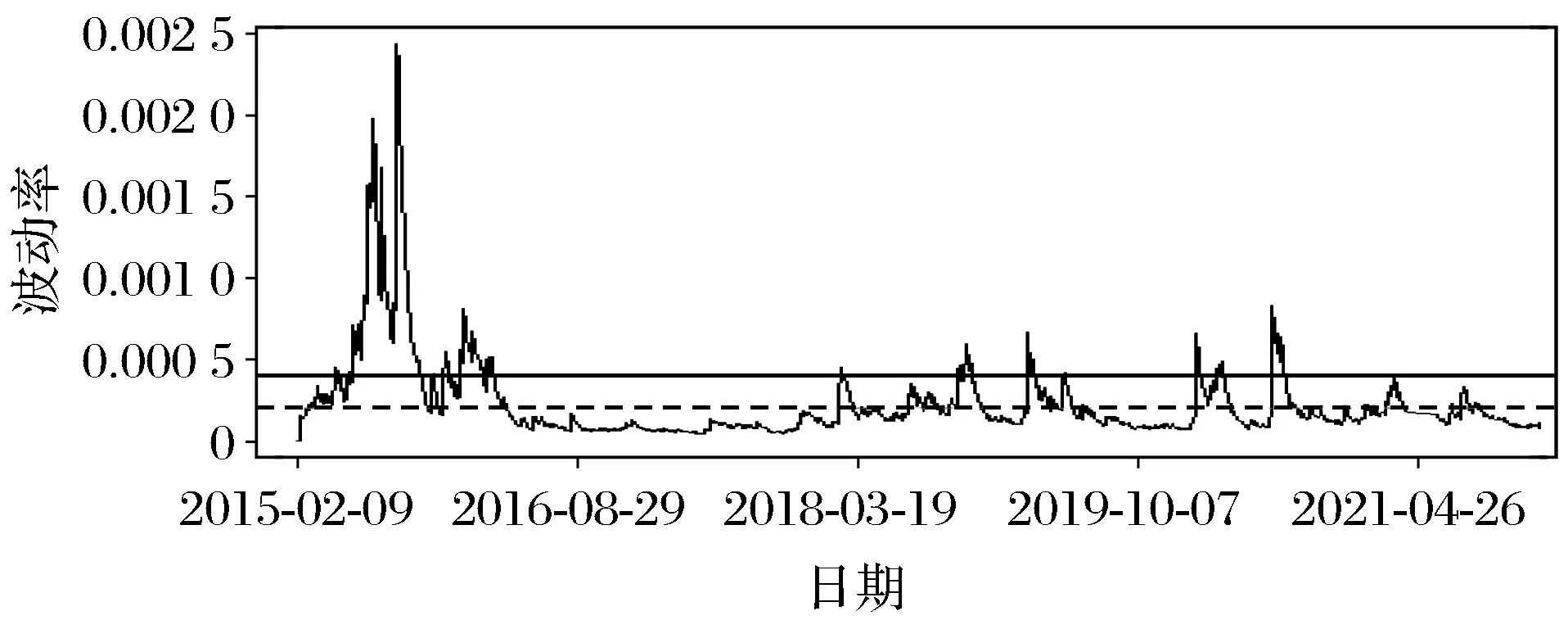
图4 GARCH波动率Fig.4 GARCH volatility

由图4可知,波动率0～0.000 2设为状态3，即平稳状态(在图4虚线以下);0.000 2～0.000 4设为状态2，即震荡状态;0.000 4～0.003设为状态1，即高波动状态(在图4实线以上)。根据波动率的不同状态,利用马尔可夫链进行概率转移,在不同情形的波动情况下与传统的GARCH模型做比较,再运用到BS模型中判断拟合程度。

根据波动率的波动情形判别将其分为3个阶段(见表6):S1为高波动状态阶段(2015年、2020年);S2为震荡状态阶段(2016年、2018年、2021年);S3为平稳状态阶段(2017年、2019年)。

表6 不同阶段状态划分

(3) GARCH-BS模型

均值模型:

rt=0.000 5-0.65AR(1)-0.94AR(2)-

0.67MA(1)0.96MA(2)+εt。

条件模型:

GARCH=2.9×10-6+0.088 2×RESID(-1)2+

0.904 0×GARCH(-1)。

根据GARCH模型计算出条件波动率代入BS模型中,假定历史波动率代入到BS模型为真实的期权价格,最后利用MSE、MAE等进行误差分析。

根据GARCH模型下残差图和残差平方图判断在建立GARCH模型后是否还存在相关性、ARCH效应,结果见图5。

图5所示残差的自相关图(见图5(a))和偏自相关图(见图5(b))的函数值都在置信区间内,即在蓝色的虚线区域范围波动。同理残差平方的自相关图(见图5(c))和偏自相关图(见图5(d))都在置信区间内不具备相关性。

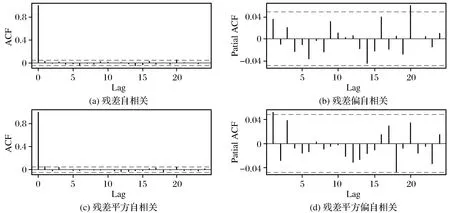
图5 GARCH模型的自相关图和偏自相关图Fig.5 Autocorrelation diagram and partial autocorrelation diagram of GARCH

检验GARCH模型是否存在ARCH效应,其结果见表7。

表7 GARCH模型下的ARCH-LM检验

由表7可知,在置信度为0.05下,ARMA(2,2)-GARCH(1,1)模型能消除ARCH效应,F统计量显著,表明GARCH模型能消除ARCH效应。

(4) 拟合图 每个阶段有不同的拟合趋势,假定行权价为3,利率为国债5年利率3.95%,到期时间按30天计算,即t=30/252=0.119 0。BS模型与GARCH-BS模型拟合性见图6。

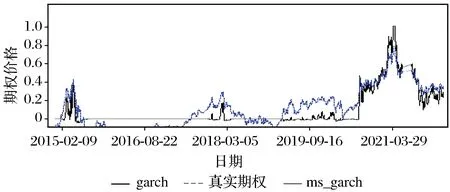
图6 BS模型与GARCH-BS模型拟合性Fig.6 Fit between BS and GARCH-BS

由图6和图1(b)对比可知,在高波动状态[0，300]、[750，1 200],即2015—2016年这段时期,GARCH模型的期权价格与真实价格差距较大；在低波动状态[500，700]、[1 200，1 500],即2016—2017年、2020—2021年这段时期GARCH模型的期权价格与真实价格差距较小。(S2)震荡状态和(S1)高波动状态二者差距较大,(S3)平稳状态下GARCH模型的理论价格和真实价格差距较小。

3 Markov-switching GARCH模型

马尔可夫结构转换GARCH模型(Markov-switching GARCH模型，简称MS-GARCH模型)是将马尔可夫模型与GARCH模型相结合，其具有很多优点:第一，经济波动趋势本身就存在不同的状态变化,相比传统刻画波动率其存在对称性的特点,这与实际的经济波动是不符的,马尔可夫模型就可以刻画经济波动的非对称信息进而提取更多的信息;第二,传统的GARCH模型只能简单将波动率提取出来,不能对未来产生预警作用,而马尔可夫模型在不同状态下有一定的转移概率,能得到不同状态下的个数和概率从而对未来的数据进行预测。

3.1 模型参数和状态转移概率

采用极大似然估计,对上证50ETF对数收益率序列运用R软件计算MS(3)-GARCH(1,1)在不同分布下的模型。模型估计结果见表8。

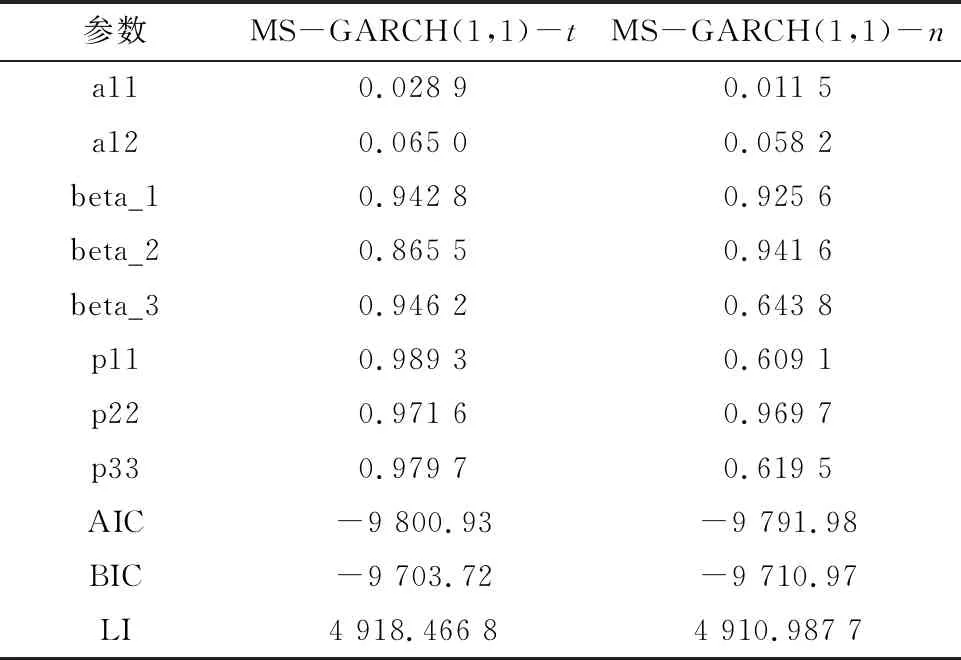
表8 MS-GARCH(1,1)模型参数估计结果

由表8可以得出T分布下的上证50ETF期权对数收益率的状态概率矩阵:

由表8亦可以得出正态分布下的上证50ETF期权对数收益率的状态概率矩阵:

从上转移概率可知,T分布下的p11=0.989 3说明在上期处于状态1(高波动状态)且在下期仍处于状态1的概率为98.93%;p22=0.971 6说明在上期处于状态2(平稳状态)且在下期仍处于状态2的概率为97.16%;p33=0.979 7说明在上期处于状态3(高波动状态)且在下期仍处于状态3的概率为97.97%。说明平稳状态和低波动状态是常态,高波动状态的概率小于平稳状态和低波动状态。由T分布下的对数转移概率矩阵可知,期权波动具有连续性，能很好地运用MS-GARCH模型,同时AIC也最小,故选择T分布下的MS-GARCH(1,1)模型。

3.2 GARCH模型与MS-GARCH模型比较

GARCH模型与MS-GARCH模型拟合状态和真实理论期权价格对比见图7。

由图7可知,3种不同状态下MS-GARCH模型的期权价格拟合要优于GARCH模型的期权价格。根据图6可知在S1高波动状态,即[0,300]时期内MS-GARCH模型要优于GARCH模型;在平稳状态S3下[1 200，1 500],从对数收益率图发现波动幅度越大越体现出MS-GARCH模型的优势。

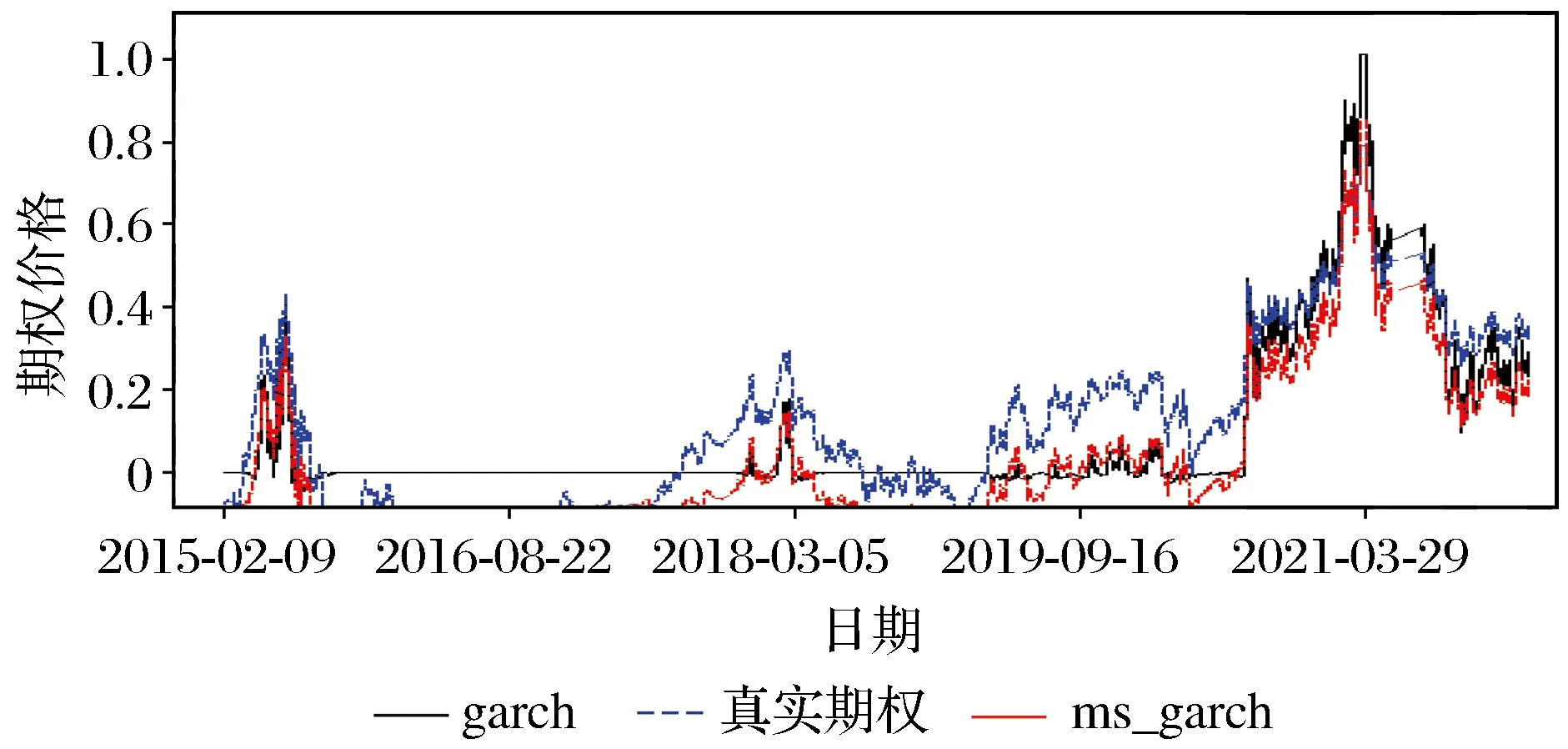
图7 GARCH-BS模型与MS-GARCH-BS模型比较Fig.7 Comparison between GARCH-BS model andMS-GARCH-BS

根据图7列出两类模型的误差分析见表9。

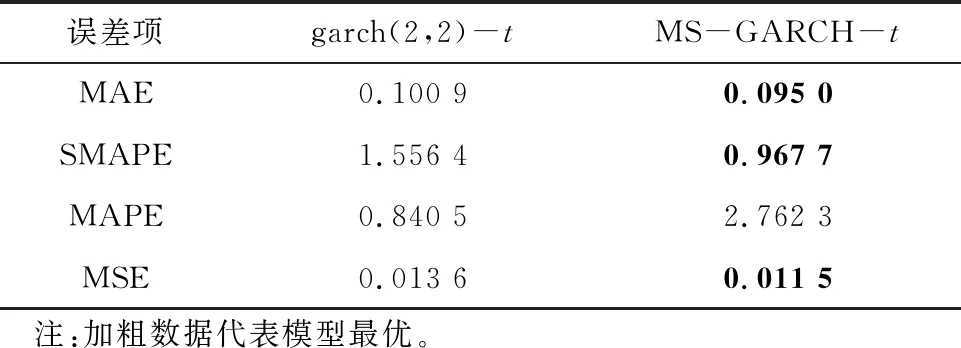
表9 两类模型的误差

由表9可知,MS-GARCH模型在拟合状态下更优于GARCH模型。平均绝对百分比误差(MAPE)分母越小则计算的数值越大,故用对称平均绝对百分比误差(SMAPE)计算更能代表误差结果,从而避免数值过大造成的影响。MS-GARCH模型的SMAPE为0.967 7;MS-GARCH模型的均方误差(MSE)为0.011 5;GARCH、MS-GARCH模型的平均绝对误差(MAE)分别为0.100 9和0.095 0。

根据表6中不同状态划分得到各个状态的误差见表10。

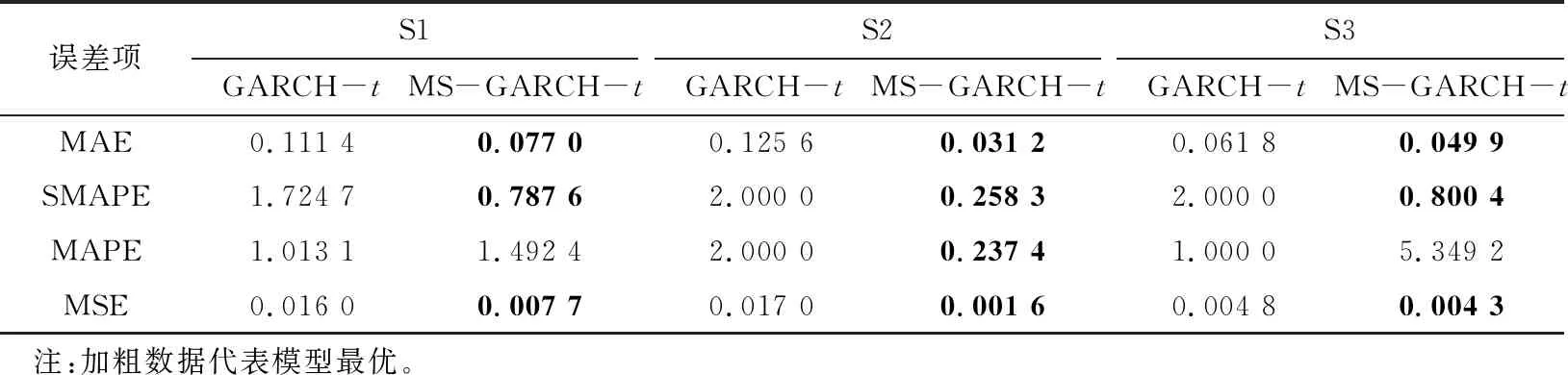
表10 两类模型不同状态的误差

由表10可知,在平稳状态(S3)下T分布的MS-GARCH模型优于T分布下的GARCH模型;在震荡状态(S2)时,T分布下的MS-GARCH模型均优于GARCH模型;在高波动(S1)时,T分布下MS-GARCH模型MAE最高,表示高波动的误差是大于震荡波动和低波动的。当MAPE数值过大时,用SMAPE判断误差分析,不同状态下SMAPE的值分别为0.787 6、0.258 3、0.800 4。综上所述在不同状态下,MS-GARCH模型拟合优于GARCH模型。

3.3 预测

通过移动平均法分别选取步长为7天、21天、60天预测期权价格，结果见图8。

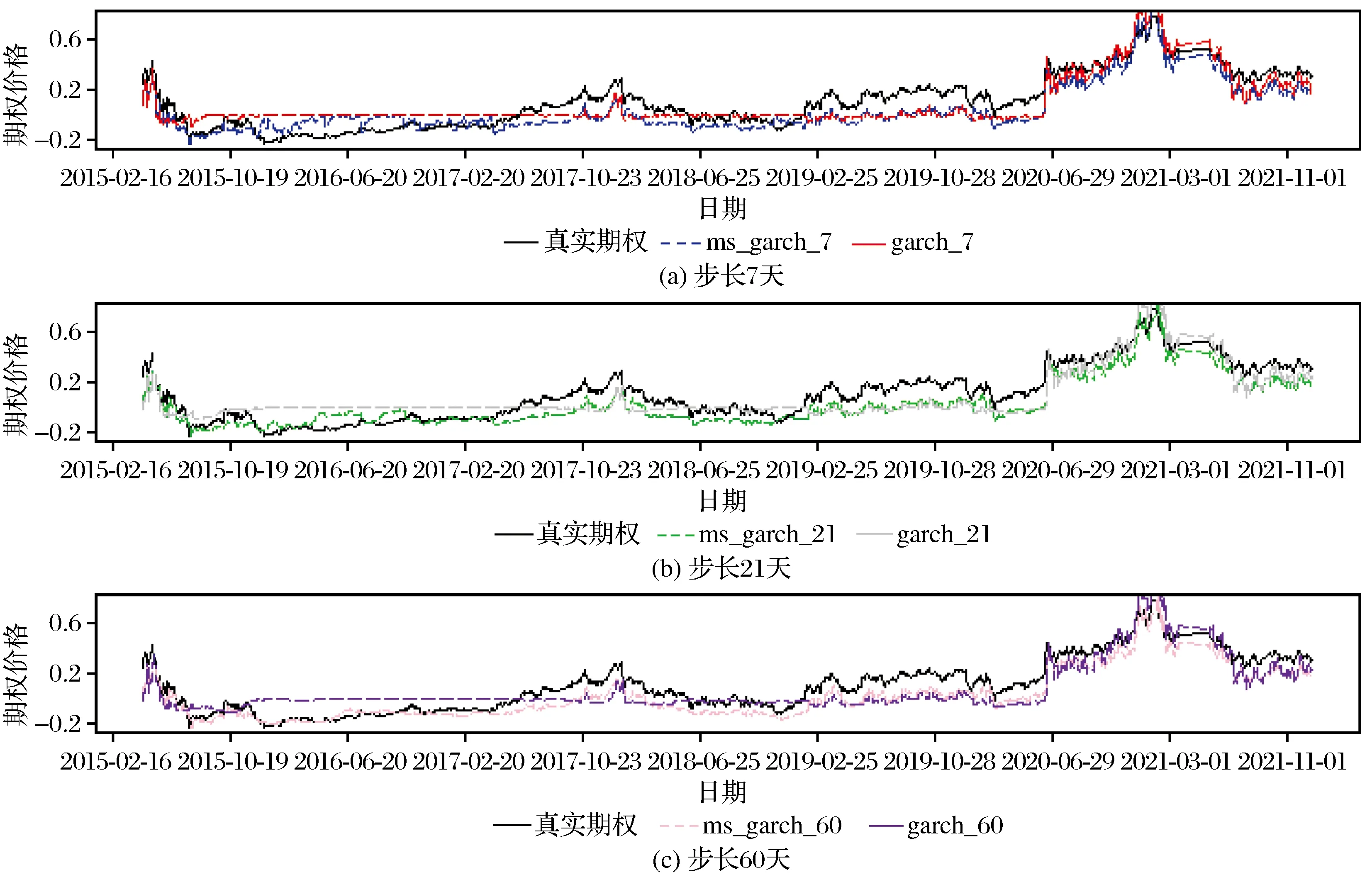
图8 不同步长预测趋势Fig.8 Prediction trend of different steps

由图8可知,从步长分别为7天(见图8(a))、21天(见图8(b))、60天(见图8(c))的趋势来看,MS-GARCH模型在高波动趋势时更接近真实期权价格,在转化状态后,MS-GARCH模型步长越长,预测越贴近真实期权价格。故通过误差分析来判断预测最好的条件。

根据不同步长得到两个模型预测误差见表11。

由表11可知,当步长为21天和60天时,MS-GARCH模型SMAPE分别为0.971 6、0.867 9;MS-GARCH模型MSE分别为0.012 4、0.010 2。由此可见MS-GARCH模型的T分布在步长为60天时为预测效果最好的模型。

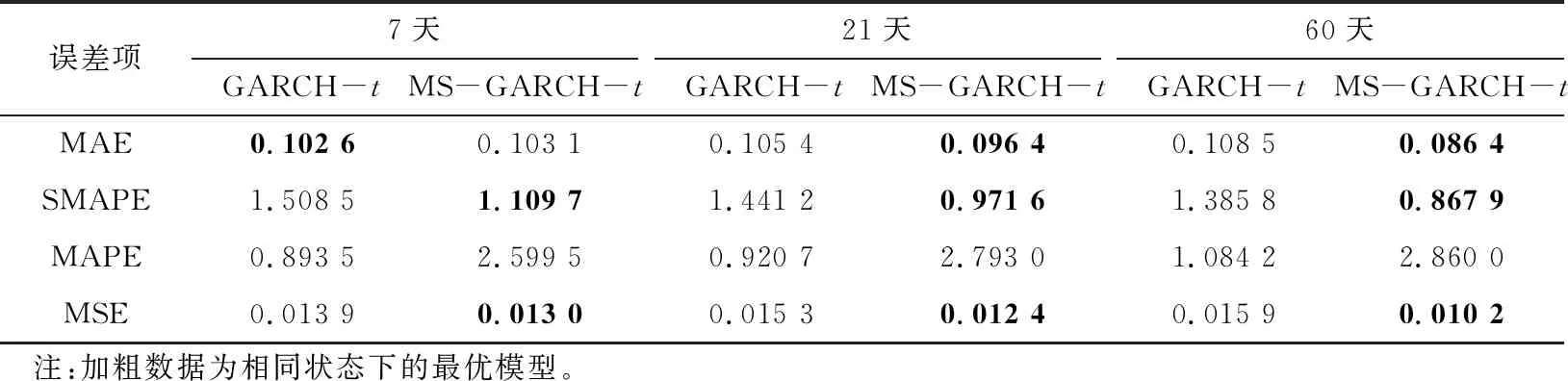
表11 两个模型的预测误差

4 结论

以上证50ETF期权为研究对象,选取2015年2月—2021年12月收盘价数据,将GARCH模型在平稳情形下划分为3个状态,根据不同状态分别进行期权价格误差分析,并且对样本内拟合和样本外预测分别进行误差分析。结果发现,在其他条件相同时,样本内拟合MS-GARCH模型优于GARCH模型;步长越长时的样本外预测MS-GARCH模型均优于GARCH模型;MS-GARCH模型的T分布在步长为60天时为预测效果最好的模型。将两种波动率与BS模型结合,采取滚动时间的方式,MS-GARCH模型在处于高波动时会优于GARCH模型,同时在高波动状态下进行更好的预测,可为金融机构和个人投资者提供参考。