超大深基坑的支护设计及变形预测研究
2023-03-03覃震林
覃震林
(柳州市勘察测绘研究院有限公司,广西 柳州 545006)
近年来,在市政工程建设过程中,地下空间的开发利用愈发显著,使得基坑工程数量不断增加,但由于基坑近接建、构筑物的限制,使得基坑支护设计显得格外重要,因此,开展基坑支护设计研究可为类似工程提供借鉴,具有重要的实用价值[1-2]。目前,已有一些学者开展了基坑支护研究,如姜林海等[3]利用BIM技术进行了基坑支护设计分析,不仅增加了参建各方的沟通,还节约了资源成本;郑刚等[4]通过数值模拟等手段开展了悬臂排桩的支护方法分析;蔡子勇等[5]对深厚软土区的地连墙基坑支护进行了优化设计及评价。
上述研究虽为基坑支护设计积累了经验,但均局限于基坑支护设计,未对设计的合理性进行探讨研究,因此,仍可进一步开展此方面的拓展研究。考虑到变形监测是基坑动态设计的必要手段,且通过变形预测能有效评价基坑稳定状态,使得通过变形预测来评价基坑支护设计的合理性是可行的。在基坑变形预测方面,也有不少学者开展了类似研究,如鲍燕妮等[6]利用ARMA模型实现了基坑变形预测;赵华菁等[7]利用神经网络算法实现了基坑地连墙的动态预测;刘锦等[8]通过GA-BP神经网络构建了基坑变形预测模型。上述研究在基坑变形预测研究方面取得了一定成果,但均未进行分项组合预测研究,即未考虑变形数据含有的不确定信息的影响,因此,基坑变形预测思路仍可进一步拓展研究。
综合上述,以龙潭医院改造基坑项目为工程背景,结合工程概况,首先开展了基坑支护方案设计,并结合变形监测成果,通过DMD模型分解出基坑变形数据的不确定信息;再利用极限学习机、M估计等构建出分项组合预测模型;最后,利用外推预测结果判断基坑支护设计的合理性,以期为类似工程提供一定的经验参考。
1 基本原理
在前述分析的基础上,进一步将分析思路总结为:在阐述基坑工程概况基础上,先开展其支护设计,然后结合基坑变形监测成果,开展其变形预测研究,以验证支护设计方案的合理性。
根据上述思路,论文涉及的理论方法主要在变形预测模型的构建中,因此,该节重点介绍预测模型的基本原理,具体如下:
结合工程实际,在基坑变形监测过程中,受若干不确定因素影响,基坑变形数据往往不是其实际变形值,会含有一定的不确定信息,即
yt=qt+wt,
(1)
其中:yt为基坑变形实测值;qt为趋势项,代表基坑实际变形值;wt为不确定项,代表基坑变形中的不确定信息。
由于不确定项的存在,会一定程度上影响预测精度,因此,在预测过程中有必要考虑基坑变形数据的分解处理,且将预测过程详述为:先对基坑变形数据进行分解处理,即分解为趋势项和不确定项;然后,以极限学习机(ELM,extreme learning machine)为基础,构建趋势项预测模型,并结合M估计进行不确定项的误差弱化预测。
1.1 变形数据的分解处理
动态模态分解(DMD,dynamic mode decomposition)是2008年提出的一种新型数据分解方法,可有效将高维非线性规律转变为低维线性规律,具有良好的适用性,因此,提出以其进行基坑变形数据的分解处理。考虑到DMD模型的基本原理已在文献[9]中详述,限于篇幅,不再赘述。
同时,为合理评价分解效果,还需进一步构建分解效果的评价指标,且考虑到以往研究多是利用单项指标进行评价,存在一定不足,因此,提出基于若干基础指标,构建出变形数据分解效果评价的综合指标p:
p=g1+g2+g3,
(2)
其中:g1、g2、g3分别为均方根误差指标、平滑度指标及信噪比指标的归一化值。
通过上述均方根误差、平滑度及信噪比指标的联合应用,保证了分解效果评价的综合性,且评价过程中,p值越大,分解效果相对越好;反之,分解效果相对越差。
因此,通过DMD模型将基坑变形数据分解为趋势项和不确定项。
1.2 趋势项的预测处理
ELM模型相较传统神经网络模型具有显著的优越性,如其具有相对更快的收敛速度和更优的可操作性,因此,以其实现趋势项预测。结合ELM模型的基本原理,其训练过程为
(3)
其中:tj为预测值;L为隐层节点数;βi、wi、bi为连接权值和阈值;g(x)为激励函数;xj为输入值。
通过ELM模型的不断训练,可实现误差的零逼近,即
(4)
结合上述,ELM模型虽具较好的预测效果,但是文献[10]中的研究表明其存在一定不足,如激励函数具有多种选择,每种激励函数的适用性存在一定差异,人为选择的合理性欠缺;连接权值和阈值是随机选择的,客观性欠缺。为切实保证趋势项的预测精度,需对前述两个问题进行优化处理,具体处理方法如下:
(1) 激励函数的优化处理。据文献[10]中的研究成果,ELM模型的常用激励函数有Hardlim型、Sigmiod型和Sine型,提出对3类激励函数均进行预测效果统计,选取预测效果最优者作为ELM模型的激励函数。
(2) 连接权值和阈值的优化处理。由于连接权值和阈值的取值范围具有连续性,难以通过逐一试算进行优化处理;同时,考虑到粒子群优化(PSO,particle swarm optimization)算法具有较强的全局寻优能力,因此,提出以其进行连接权值和阈值的优化处理。结合PSO算法的基本原理,可将其寻优过程详述为:
初始化基础参数。将粒子群规模设置为600,每个粒子的维数设置为2,分别代表连接权值和阈值,最大迭代次数设置为700次,其余参数随机设置。
更新迭代寻优。以每个粒子的预测值与实测值为基础,将二者差值的绝对值作为对应粒子的适应度值,并通过对比,初步确定出最优的全局适宜度值;同时,再进一步更改每个粒子的速度和位置参数,以实现粒子的更新迭代,并适时更新全局适宜度值。
参数输出。当达到期望误差或最大迭代次数后,将最后的全局适应度值所对应的参数输出,即可完成连接权值和阈值的优化处理。
通过上述优化处理,有效保证了ELM模型参数的最优性,也奠定了趋势项高精度预测的基础;同时,为便于后续分析,将激励函数优化后的模型命名为初步优化ELM模型,将经过PSO算法再次优化后的模型命名为PSO-ELM模型。
1.3 不确定项的弱化处理
通过优化处理虽然保证了趋势项预测模型的预测精度,但是值得指出的是,趋势项具有较强的非线性特征,PSO-ELM模型也难以完全刻画其变形规律,即其预测结果仍会存在一定的预测误差;为保证基坑变形最后预测结果的精度,将趋势项的预测误差叠加至不确定项wt中,组成新的不确定项序列。
由于不确定项序列具有相对更强的非线性特征,结合文献[10]中的成果,再利用M估计实现其弱化处理,即
(5)
在式(5)原则基础上,通过最小二乘估计构建出权值矩阵β:
β=(HTPH)-1HTPT,
(6)
其中:P为权函数矩阵;T为因变量矩阵;H为自变量矩阵。
将M估计的弱化预测结果叠加至趋势项的预测结果中,所得叠加值即为最终预测结果,为便于后续分析,将M估计处理后的模型命名为R-PSO-ELM模型。
2 实例分析
2.1 工程概况
在广西壮族自治区龙潭医院改造基坑中,主要涉及3栋楼,其中2栋属于高层,1栋属于多层,且基坑西侧为医院进出道路,南侧为羊角山路,东、西两侧均有局部近接既有建、构筑物;结合上部结构设计成果,本次修建房屋高度在20~38 m之间,设一层连通式地下室,基坑支护周长合计约360.4 m,支护面积约6 705.3 m2,坑底面积约5 673.2 m2,属超大基坑。同时,基坑开挖深度2.4~7.1 m,绝大部分范围内的开挖深度大于5 m,则其亦属深基坑。
根据勘察成果,整个场地南面地势稍低,北面稍高,实测场地地面标高在81.37~87.41 m之间。场区地貌属柳南山前岩溶准平原。工作区土层主要为碳酸盐岩系经红土化作用而形成的红黏土,岩性可分为杂填土、表层红黏土、可塑-硬塑红黏土;下覆基岩为白云质灰岩,岩芯可见溶孔,说明其溶蚀作用明显,且孔内由黏性土充填。
结合区域地质资料,工作区地质构造不发育。在水文地质条件方面,地表水以工作区东面约3.0 km处的柳江为主,与场区地下水具有一定的水力联系。地下水可分为两类,即上层滞水和岩溶水,其中上层滞水主要赋存于杂填土、红黏土的微裂隙中,水位埋深0.3~4.5 m,年变幅3~5 m,对基坑施工具有直接影响,建议进行明排疏干;岩溶水主要赋存于基岩溶蚀空洞和管道中,水量丰富,具有一定的承压特征,主要接受降水补给。
结合勘察结果,场地遇洞隙率为59.4%,线岩溶率为20.8%,结合《广西壮族自治区岩土工程勘察规范》[11],该场地岩溶发育等级为强烈,主要表现为岩面起伏不平,浅层溶洞(沟、槽)较发育,规模纵深不一。
2.2 基坑支护设计研究
基坑开挖深度2.4~7.1 m,绝大部分范围内的开挖深度大于5 m,属深基坑,加之基坑所处地区岩溶发育,工程重要性高,使得开展基坑支护设计研究具有较强的必要性。
(1) 支护方案的对比及确定 结合基坑实际及相关工作经验,该基坑的拟用支护方案可设定为悬臂排桩支护、桩锚支护、锚喷支护及放坡,并将各方案的技术及造价对比分析如下:
悬臂排桩支护。该支护方案虽能进行垂直开挖,以达到充分利用场地空间的目的,但若基坑所处地质条件差、开挖较深时,该方案存在位移变形大的缺点,且单纯的悬臂支护方案会存在工期长、造价高等缺点。
桩锚支护。该方案可通过各个支护结构的共同作用,形成刚度大、安全牢固的支挡体系,可有效预防及控制位移变形,且该支护方案亦可垂直开挖,不仅可减少土方开挖量,而且能充分利用场地空间,但该方案也存工期相对较长、造价较高的缺点。
锚喷支护。该方案所需施工设备简单、支护灵活、技术成熟,可边支护边施工,并具有节约工期、造价较低等优点,但是此支护方案的位移变形相对偏大,不适用于变形控制严格的基坑。
双排桩支护。该方案的支护体系具有较大的刚性,能有效控制基坑位移,但其也具有工期相对较长、造价高等缺点。
放坡开挖。该方案在造价、工期及安全性方面均具有明显的优点,但对场地条件要求较高,即需要较宽的可利用空地。
由于基坑北侧有保留建筑3栋,建筑基础距基坑开挖边界线5~10 m;东侧有保留建筑2栋,建筑基础距地下室结构边线3.8~5 m,这些建筑物均修建于上世纪70、80年代,采用条形浅基础,基础埋深在1.5 m左右,由于建筑物修建年限较为久远,基础埋深较小,建筑抗变形能力及稳定性均较差,对基坑位移变形较为敏感。
综上所述,为充分保证基坑开挖安全,也为充分节约造价成本,工程采用分段支护设计,且设计方案主要包括放坡、挂网喷浆、管桩及支护桩等支护形式。
(2) 支护设计内容 进一步开展基坑支护设计内容详述,基坑支护设计平面图如图1所示。

图1 基坑支护设计分段示意图Fig.1 Sectional diagram of foundation pit support design
结合图1,该基坑的支护可划分为9段,并以支护分段为基础,从控制点A开始,顺时针阐述各段支护设计内容,具体如下:
AB段:此段采用“挂网喷浆+锚杆”的支护手段,其中基坑边坡按1∶0.2的坡率进行开挖,全面积挂网喷浆,锚杆长度6 m,采用1根直径为20 mm的钢筋,倾角20°,横向间距1.4 m,纵向间距1.1 m,坡顶采用C20混凝土进行硬化,厚度10 cm。
波磨产生的源头在于钢轨表面存在不平顺,当列车高速通过不平顺钢轨时,会产生高频瞬时冲击载荷。长期以往,最终会在钢轨不平顺处产生接触疲劳。伴随着接触疲劳的是车轮和钢轨之间的接触振动和摩擦振动。
Bb段:此段采用“钢管桩+挂网喷浆”的支护手段,其中管桩为双排Φ130 cm@400 cm钢管桩,同样进行全面积挂网喷浆,桩顶采用500 mm×400 mm压梁,其材料为C30钢筋混凝土。
bC段:此段采用“挂网喷浆+钢管桩+锚杆”的支护手段,其中挂网喷浆为全面积进行,管桩为单排Φ130 cm@1200 cm钢管桩,锚杆长度6~9 m,采用1根直径为20 mm的钢筋,倾角20°,横向间距1.2 m,纵向间距1.0 m。
CD段:此段采用“支护桩+锚索”的支护手段,其中支护桩采用直径1 m的钢筋混凝土桩,间距2 m,桩长以入岩2 m控制,桩顶施做1 000 mm×800 mm的C30冠梁,锚索长度16~18 m,共拟布设两排,横向间距2 m,纵向间距2.5 m。
DE段:此段采用“支护桩”的支护手段,其桩径为1 m,横向间距2 m,桩顶施做1 000 mm×800 mm的C30冠梁,且其地表采用C20混凝土硬化,厚度10 cm。
EF段:此段采用“挂网喷浆+锚杆”的支护手段,其中基坑边坡开挖坡比按1∶0.4进行,全面积挂网喷浆,锚杆长度5~6 m,采用1根直径为20 mm的钢筋,倾角20°,横向间距1.3 m,纵向间距1.1 m。
FG段:此段采用“支护桩”的支护手段,其桩径为1 m,横向间距2 m,桩顶施做1 000 mm×800 mm的C30冠梁,且其地表采用C20混凝土硬化,厚度10 cm。
GH段:此段采用“放坡”支护手段,放坡坡比控制在1∶1.25~1∶1.3之间,坡顶在施工前先进行场地平整。
HA段:此段采用“挂网喷浆+锚杆”的支护手段,其中基坑边坡开挖坡比按1∶0.4进行,全面积挂网喷浆,锚杆长度4.5 m,采用1根直径为20 mm的钢筋,倾角20°,横向间距1.4 m,纵向间距1.1 m,坡顶采用C20混凝土进行硬化,厚度10 cm。
2.3 变形预测分析
由于基坑支护设计多采用“动态设计”的原则,因此,在其施工过程中的变形监测显得格外重要;同时,考虑到基坑变形预测能为其安全评价提供一定的指导,所以进行变形预测分析有较强的必要性。
在基坑变形监测中,桩顶水平位移是必测项,其极限预警值为25 mm,共布设了21个监测点(布置情况详见图1),其中B02、B11和B14监测点的水平位移值相对最大。经过28个周期的变形结果统计,得到三者的最终变形值分别为15.95 mm、19.47 mm和17.20 mm,变形曲线如图2所示。
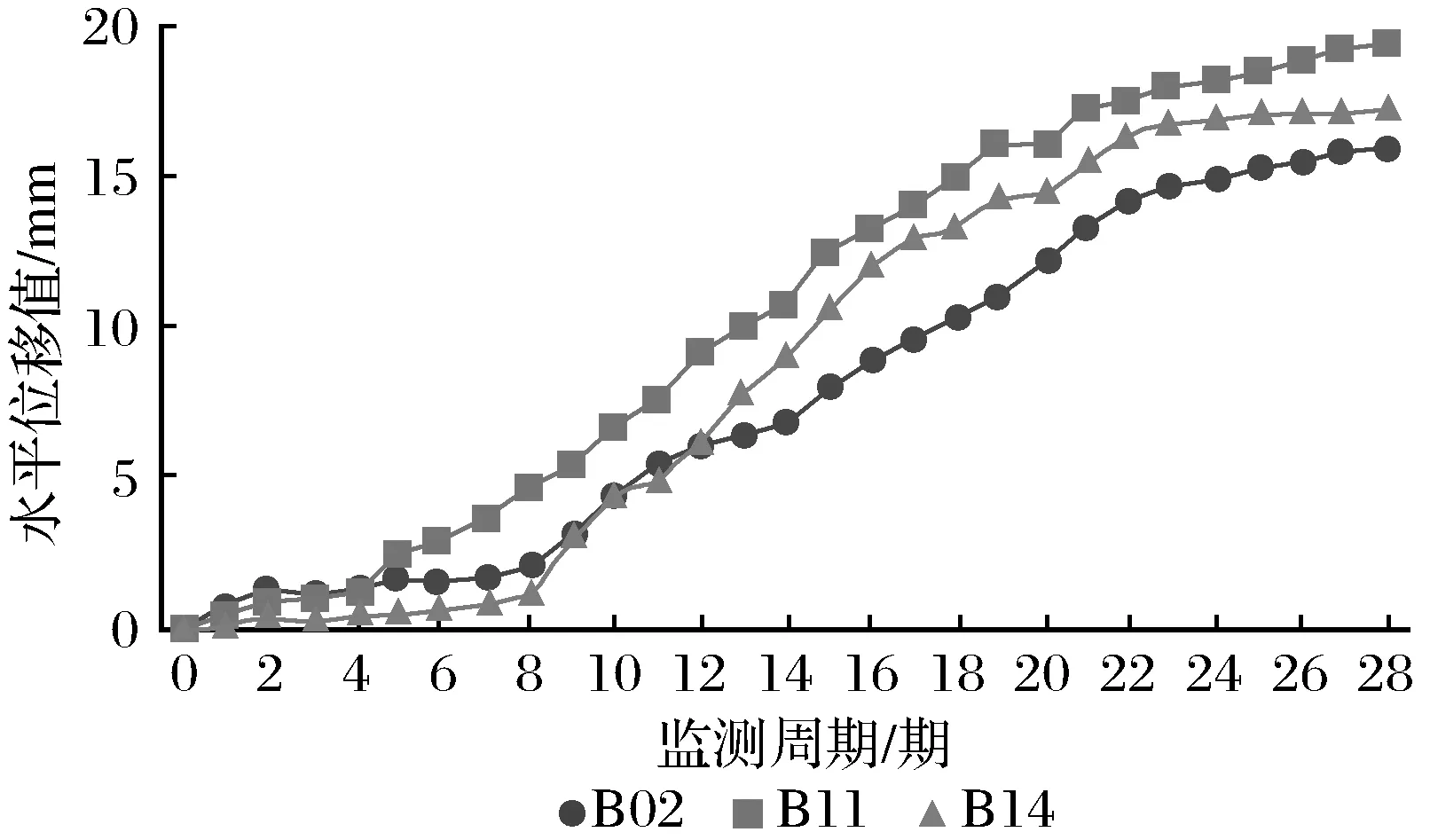
图2 基坑水平位移变形曲线Fig.2 Horizontal displacement of deformationcurve of foundation pit
为充分验证R-PSO-ELM模型的有效性,对上述3个监测点均进行变形预测研究。
(1) 变形数据的分解处理 利用DMD模型对基坑水平位移数据进行分解处理,且为佐证DMD模型的有效性,再提出用若干db小波和sym小波进行对比分解处理,经统计各类分解方法的结果如表1所列。从表1可见,不同db小波和sym小波的分解效果存在一定差异,且二者的评价指标均值分别为2.410和2.419,明显小于DMD模型的评价指标值2.714,说明DMD模型相较前二者具有相对更优的分解效果,分解能力更加明显。同时,由于DMD模型的评价指标P值已达2.714,趋近于3,说明其分解效果较优,适用于基坑变形数据的分解处理。

表1 变形数据的分解结果
(2) 变形预测结果 通过DMD模型的数据分解处理,将基坑水平位移数据分解为趋势项和不确定项,采用R-PSO-ELM模型对其进行分项组合预测研究,且训练样本集为1~23周期的数据,验证样本集为24~28周期的数据。为充分了解各分项优化预测阶段的效果,提出以B02监测点为例,详述各阶段的预测结果。另外,预测效果的评价指标确定为平均相对误差和训练时间,前者主要用于评价预测精度,其值越小越好;后者主要用于评价收敛速度,其值越小,说明收敛速度越快。
① B02监测点的预测结果。趋势项预测结果:首先对ELM模型的激励函数进行优化筛选,得出3类激励函数的预测结果,如表2所列。

表2 不同激励函数的预测结果
从表2可见,不同激励函数的预测结果存在明显差异,在预测精度方面,Sigmiod函数的平均相对误差值为2.82%,相对最小,其次是Hardlim函数和Sine函数,二者的平均相对误差值分别为3.28%和3.41%,得出Sigmiod函数的预测精度相对最高;在收敛速度方面,Sigmiod函数的训练时间相对最短,为68.22 ms,得出Sigmiod函数的收敛速度相对最快。
在工程实例中,Sigmiod函数不仅具有相对更优的预测精度,还具有较快的收敛速度,预测效果相对较优,因此,确定其为ELM模型的激励函数。
利用PSO算法优化ELM模型的连接权值和阈值,且为验证PSO算法优化效果,对其优化前后的预测结果进行统计,结果如表3所列。从表3可见,在初步优化ELM模型的预测结果中,得相对误差变化范围为2.63%~3.03%,平均相对误差为2.82%;在PSO-ELM模型的预测结果中,得相对误差变化范围为2.17%~2.29%,平均相对误差为2.21%。二者对比得出经PSO算法的优化处理,趋势项的预测精度得到明显提高,验证了PSO算法对ELM模型参数的优化能力,也说明在趋势项预测模型构建过程中的逐步优化处理是有必要的。
综上所述,在趋势项预测结果中,通过激励函数、连接权值和阈值的优化处理,逐步提升了预测精度,且PSO-ELM模型的平均相对误差为2.21%,说明趋势项具有较优的预测效果。
不确定项的弱化预测结果:由表3可知趋势项预测结果仍存在一定的预测误差,将其预测误差叠加至不确定项中,以组成新的不确定项序列,并利用M估计实现其弱化处理,所得预测结果如表4所列。从表4可见,经M估计对不确定项序列的弱化处理,所得预测结果的相对误差间于2.03%~2.21%,平均相对误差为2.12%,相较趋势项预测精度有进一步的提升,且预测效果较优,验证了M估计对不确定项序列具有较优的弱化效果。
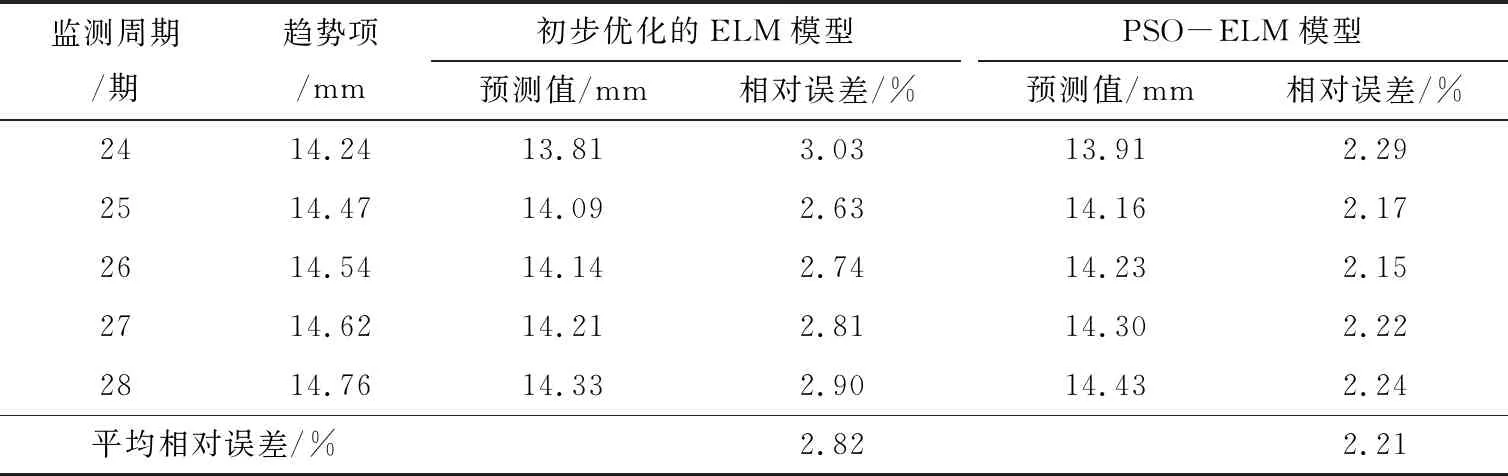
表3 B02监测点在不同优化阶段的趋势项预测结果
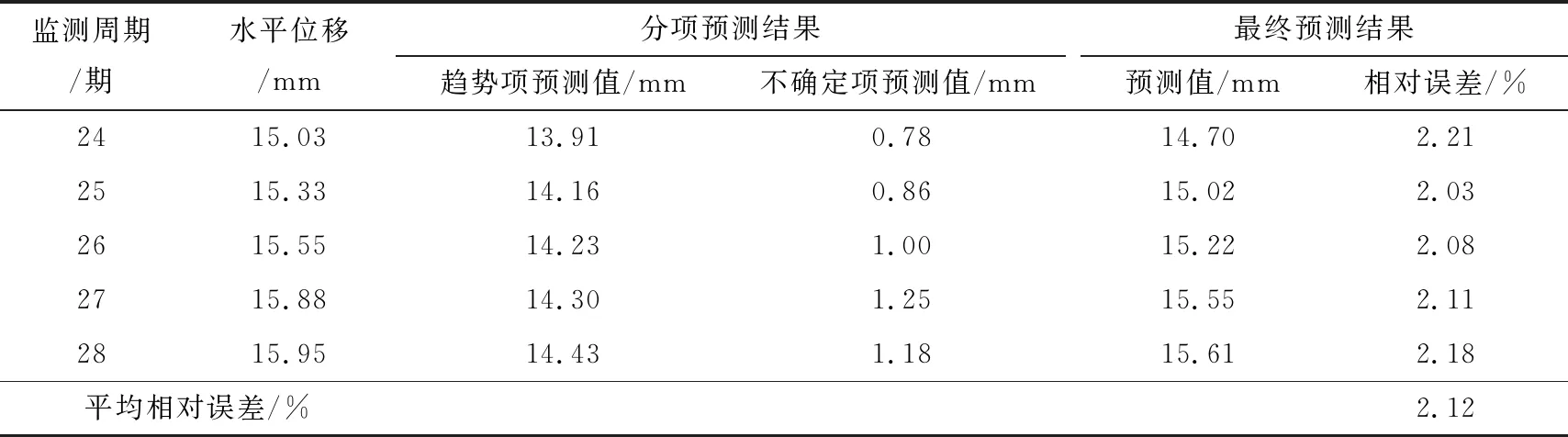
表4 B02监测点的最终预测结果
为进一步验证各分项预测阶段的合理性,再以训练时间为指标进行收敛速度评价,并按照组合流程,进行阶段性划分,具体如下:
阶段1:初步优化的ELM模型;
阶段2:PSO-ELM模型;
阶段3:R-PSO-ELM模型。
对上述3个阶段的训练时间进行统计,结果见图3。从图3可见,随各分析预测阶段的递进组合,训练时间由68.22 ms降低至59.35 ms,说明随优化、组合的持续进行,能有效增加预测模型的收敛速度,验证了预测思路的合理性。

图3 不同阶段的训练时间对比Fig.3 Comparison of training time in different stages
通过对B02监测点的预测结果分析,得出分项组合预测思路不仅能有效提高预测精度,还能有效节约训练时间,初步验证了R-PSO-ELM模型在基坑变形预测中的适用性。
② 所有监测点的预测结果。在前述B02监测点预测结果分析基础上,再对其进行外推预测,外推周期数为4期,并对其余两个监测点进行类似预测,所得结果如表5所列。从表5可见,3个监测的平均相对误差在2.06%~2.12%之间,变化范围较小,说明R-PSO-ELM模型的预测效果不仅具有较优的预测精度,还具有较强的稳定性。根据外推预测结果,得出3个监测点的后续变形仍会进一步增加,但增加速率较小,已趋于稳定。对3个监测点的训练时间进行统计,得出B02、B11和B14监测点的训练时间分别为59.25 ms、61.44 ms和58.36 ms,均具有较短的训练时间,即具有较快的收敛速度。
总结基坑变形预测结果,可以得出龙潭医院改造基坑的变形趋于稳定方向发展,且最大预测值均在预警值范围内,验证了本次基坑支护设计方案是合理的。
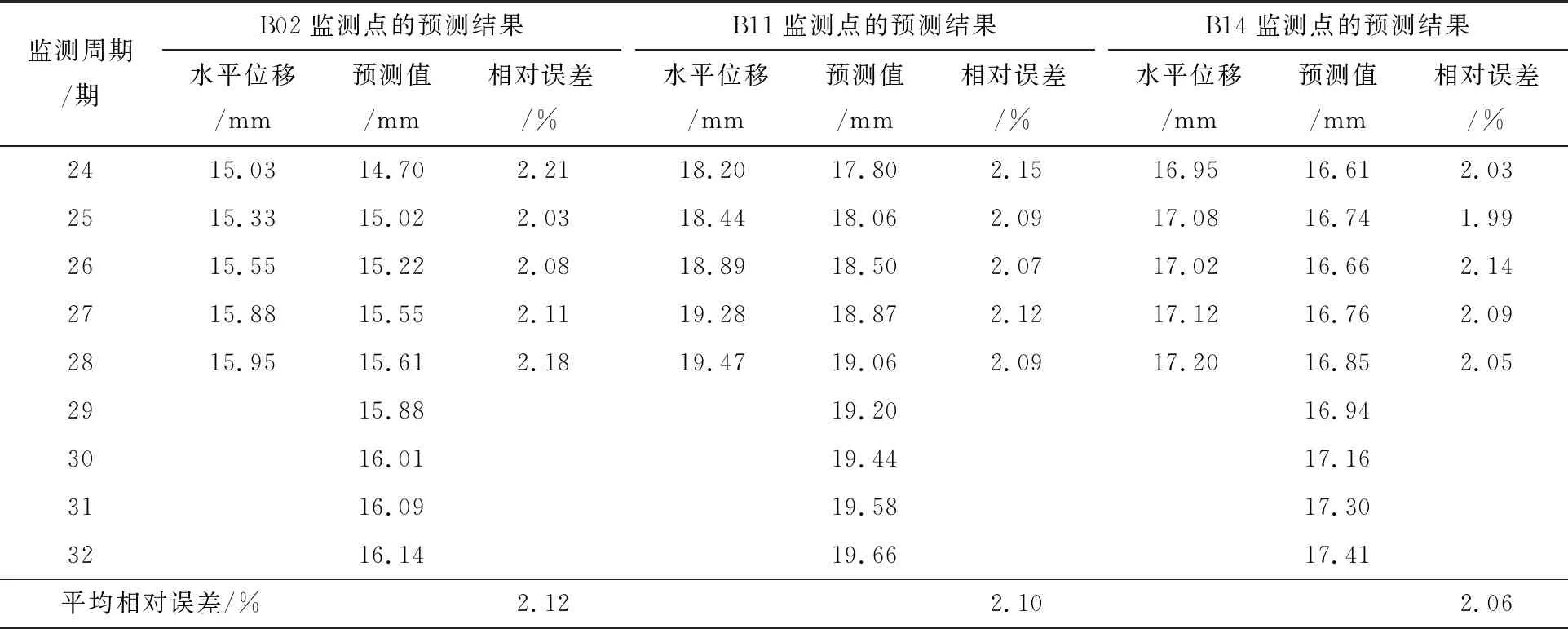
表5 所有监测点的预测结果
3 结论
通过对龙潭医院改造基坑的支护设计及变形预测进行研究,主要得出如下结论:
(1) 由于基坑开挖范围大、深度深,加之近接建、构筑物对位移变化较为敏感,因此,在基坑支护方案的设计过程中,应结合工程实际进行分段支护设计,即该基坑的设计方案主要包括放坡、挂网喷浆、管桩及支护桩等支护形式。
(2) 在变形预测中,DMD模型相较传统分解方法具有相对更优的分解效果,且分项递进组合不仅能有效提高预测精度,还能提升收敛速度,充分验证了R-PSO-ELM模型在基坑变形预测中的适用性;同时,通过外推预测得出基坑变形趋于稳定方向发展。
(3) 以变形监测结果为基础,开展了基坑变形预测研究,并以预测结果侧面验证了支护设计方案的合理性,建议后续可在此基础上进一步利用数值模拟,开展基坑稳定性评价,以充分佐证支护设计方案的合理性。
