基于正交试验的双流道泵叶轮优化设计与试验
2023-03-03盛建萍王晓川
刘 哲,盛建萍,王晓川
(1.上海凯泉泵业(集团)有限公司,上海 201804; 2.合肥凯泉电机电泵有限公司,安徽 合肥 230000;3.武汉大学动力与机械工程学院,湖北 武汉 430072;4.水射流理论与新技术湖北省重点实验室,湖北 武汉 430072)
潜水排污泵作为一种典型的机电一体化设备,广泛应用于污水处理、市政排污、水利环境治理等工程领域[1-2]。在排污泵设计中,对其无堵塞性要求很高。而无堵塞性主要取决于叶轮的结构形式,这就要求叶轮具有较大的过流面积。目前,潜水排污泵叶轮形式主要有单流道、双流道、叶片等[3],与单流道叶轮相比,双流道叶轮对称的结构特点,使其具有较好的平衡性,运行平稳;与叶片式叶轮相比,双流道泵无堵塞性能好,尤其适用于输送含大颗粒长纤维的污水介质[3]。因此,双流道叶轮因具有独特的优势,是排污泵较常采用的叶轮结构形式[4]。
目前,许多学者对双流道泵进行了大量的研究。赵斌娟等[5]采用不同的流道面积变化规律研究了双流道泵内部的流动变化;程效锐[6]应用三维数值模拟对双流道泵在不同工况下的内部流动进行了性能预测;仇晶等[7]研究了隔舌位置对双流道泵水力性能及结构性能的影响。双流道泵的性能受多种因素影响,而正交试验设计是一种研究多因素多水平的设计方法,它可以从全面试验中挑选出均衡分散。齐整可比的点进行试验,其优点是通过合理的试验方案来减少试验次数,缩短试验周期,是一种高效、快捷、经济的试验设计方法[8-12]。
双流道泵的流道空间形状由轴面形状、平面流道结构和流道中线共同决定。其中,流道中线对双流道叶轮性能影响尤为重大,因此文中选择控制流道中线的叶轮前盖板圆弧R1、后盖板圆弧R2、平面流道中线包角ψ和系数m这4个参数为设计因素,应用正交试验设计法设计计算方案,并在相同的工况下,借助CFD技术对方案进行性能预测,探寻最优的流道中线参数组合,为双流道泵的水力优化提供参考。
1 设计模型与数值模拟
1.1 计算模型
研究对象是一台比转速为67的双流道泵。主要设计参数如下:额定流量Qd=10 m3/h,额定扬程H=16.5 m,额定转速n=2 840 r/min。叶轮为双流道形式,如图1所示。

图1 双流道叶轮Fig.1 The double-channel impeller
1.2 数值模拟
采用定常流动的模拟方法对原始泵进行水力性能分析。数值模拟计算域包括进水段、叶轮、蜗壳和出水段4个部分,如图2所示。考虑到计算的收敛性,进水段和出水段的长度取其相应直径的4倍。计算域采用适应性较强的四面体非结构化网格。数值模拟以清水为介质,采用RNG-κ~ε湍流模型。由于叶轮与蜗壳之间存在相对运动,使用多重参考坐标系法。叶轮设置为转动区域,蜗壳、进水段、出水段设置为静止区域。进口边界采用速度进口,出口边界设为自由出流,叶轮设置为旋转部件,转速为2 840 r/min,其他部件为静止域,固体壁面采用无滑移绝热边界条件,靠近壁面区域采用标准壁面函数。
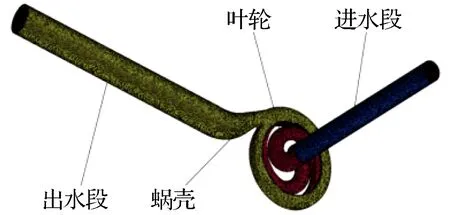
图2 计算域与计算网格Fig.2 Comparison domain and mesh of the double-channel pump
为了降低网格数量对计算结果的影响,需要对网格进行无关性验证。选取扬程作为网格无关性的评价标准,划分7套不同数量的网格,利用CFD软件对设计工况点的扬程进行计算,如图3所示。模拟结果表明,整泵网格数在达到310万之后,扬程趋于稳定。最终选用340万的网格数进行后续数值模拟计算。
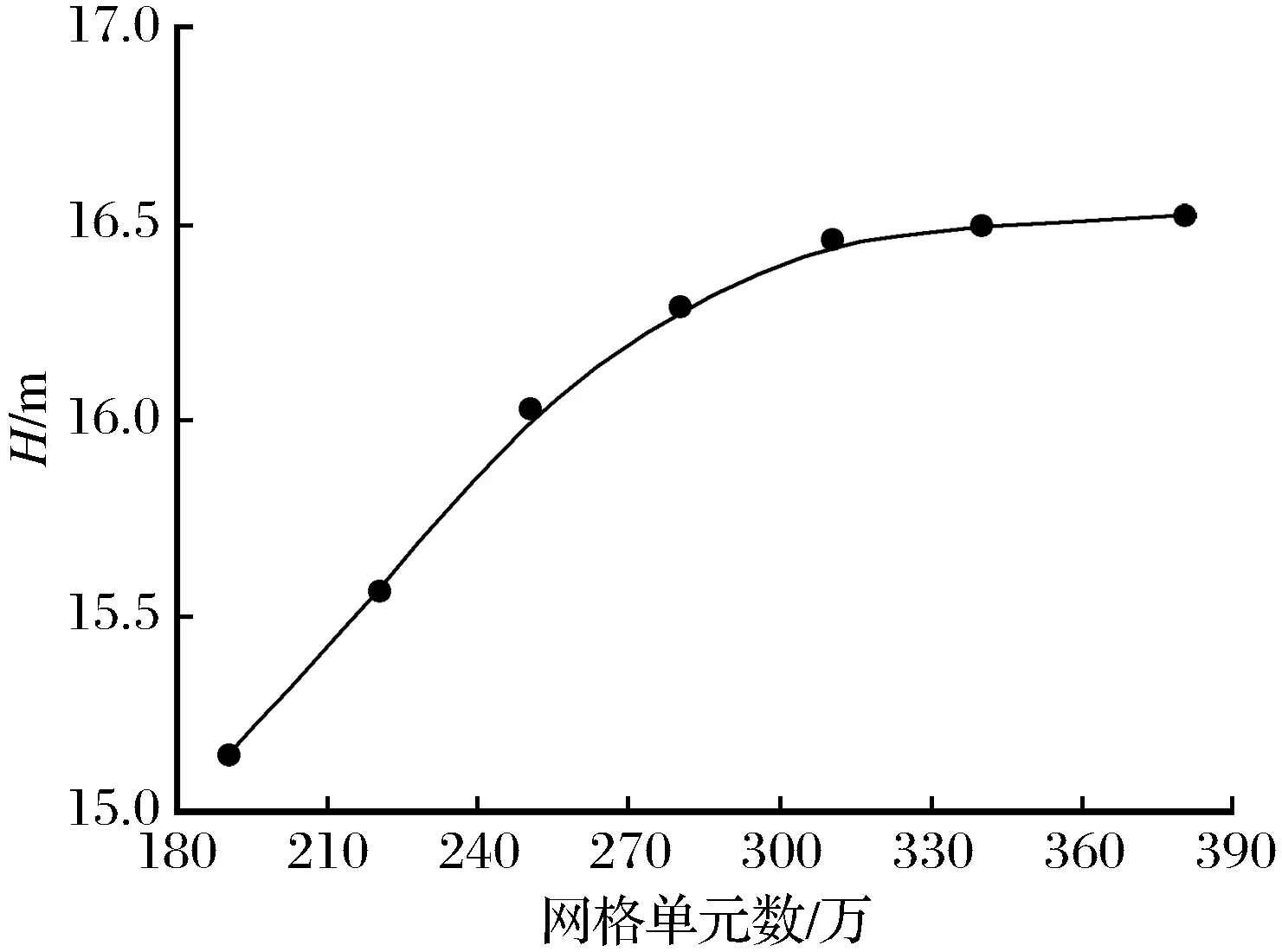
图3 网格无关性验证Fig.3 Grid dependence analyses
1.3 数值模拟结果与试验验证
原始模型试验在合肥凯泉电机电泵有限公司综合性能测试试验台进行,试验台满足国家标准。抽送介质为清水,泵出口管路直径为DN50,管路上设有压力传感器、电磁流量计和电动闸阀,通过控制电动闸阀的开度实现不同工况点的测试。数值模拟结果与试验结果对比如图4所示。由图4可以看出,在0.85Qd~1.36Qd工况范围内,扬程预测值与试验值相差不大,误差均在5%以内;在0.85Qd工况点效率误差为8.52%,其他工况点误差均在5%以内,符合工程实际,说明该数值模拟方法可以应用于后续计算。

图4 原始模型试验结果与数值模拟结果对比Fig.4 Comparison between CFD and experimental results
2 正交试验
在双流道的水力设计中,流道中线不仅影响着内流道和外流道的结构,而且对泵的性能有很大影响。双流道叶轮的流道中线是一条空间三维曲线,由轴面流道中线和平面流道中线相交获得。轴面流道中线是轴面图内切圆圆心的连线;平面流道中线绘制公式为
r=aθm,
(1)
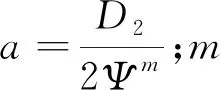
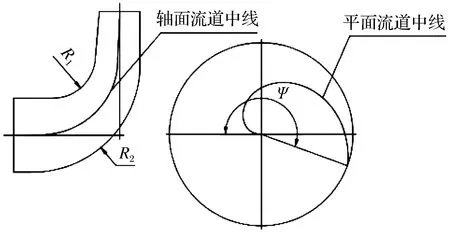
图5 叶轮流道中线Fig.5 The flow mean line of impeller
正交试验设计法是一种利用标准化的正交表来安排试验方案,分析多因素试验的方法。保持叶轮其他几何参数不变,以控制轴面流道中线形状的主要参数叶轮前盖板圆弧R1、后盖板圆弧R2、平面流道中线包角Ψ和系数m为设计因素,每个因素取3个水平,设计因素与各水平取值如表1所列。选用标准的L9(34)正交表设计了9组叶轮方案,如表2所列。

表1 因素水平
3 结果分析
3.1 性能分析
运用CFD软件对设计的9副叶轮分别组装同一个蜗壳进行三维数值模拟,计算额定工况Qd=10 m3/h下各个方案的扬程、效率预测值,数值模拟结果见表3。
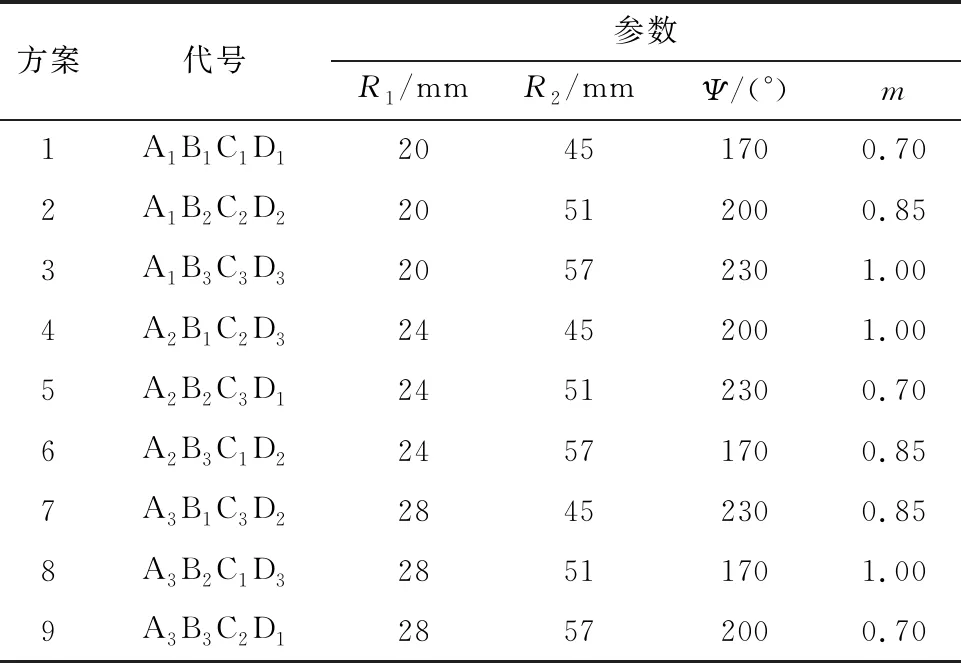
表2 试验方案
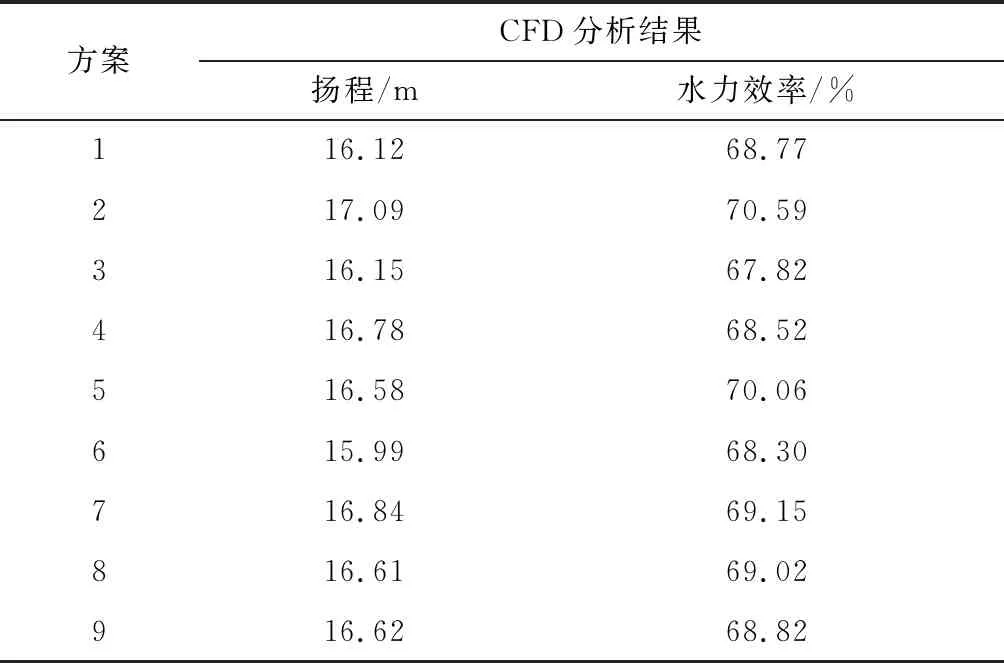
表3 数值模拟结果
从表3中的正交试验方案数值模拟结果可知,方案2的扬程和效率均最高。
3.2 极差分析

为了直观分析出单个因素不同水平对双流道泵性能的影响,以各因素水平为横坐标,扬程和效率为纵坐标,分别绘制因素水平与扬程和效率的关系图,如图6所示。对于单个因素而言,前盖板圆弧R1各水平对扬程的影响顺序为A3>A2>A1,对效率的影响顺序为A1>A3>A2;后盖板圆弧R2各水平对扬程的影响顺序为B2>B1>B3,对效率的影响顺序为B2>B1>B3;包角Ψ各水平对扬程的影响顺序为C2>C3>C1,对效率的影响顺序为C2>C3>C1;系数m各水平对扬程的影响顺序为D2>D3>D1,对效率的影响顺序为D2>D1>D3。

表4 极差分析

图6 性能指标与因素的关系Fig.6 Relationship between factors and performance indicator
综上所述,效率最佳的组合为A1B2C2D2,即正交试验方案2,其组合参数为:R1=20,R2=51,Ψ=200°,m=0.85。
4 内部流动分析
叶轮最优方案的参数组合是:R1=20,R2=51,Ψ=200°,m=0.85,即方案2。文中分析了0.85Qd~1.36Qd下优化模型的外特性曲线,并与原始模型进行对比分析,如图7所示。泵在各工况点,效率均有不同程度提升,在额定工况点Qd=10m3/h,优化后的泵较原始泵扬程提高0.59m,效率提高了5.4%,在大流量工况下,优化后的泵效率提升幅度更大且高效点偏向大流量区域,降低了泵在大流量区域运行时过载的风险;当Qd>9m3/h时优化模型的扬程均高于原始模型扬程,且优化后泵的扬程曲线变得平坦。额定工况下优化前后水泵中间截面的流线分布对比如图8所示,液体进入蜗壳扩散段后,原始泵流态紊乱,经过叶轮的优化改进后,蜗壳扩散段的流态得到了明显改善,叶轮与蜗壳匹配更合理。
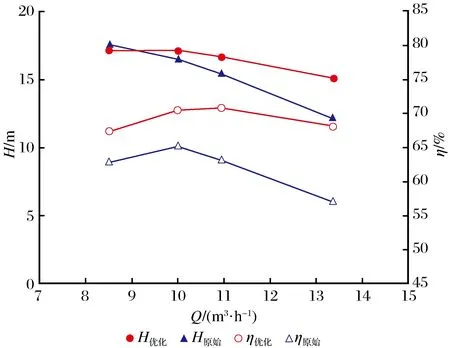
图7 优化前后外特性曲线对比Fig.7 Comparison of pump performance beforeand after optimization
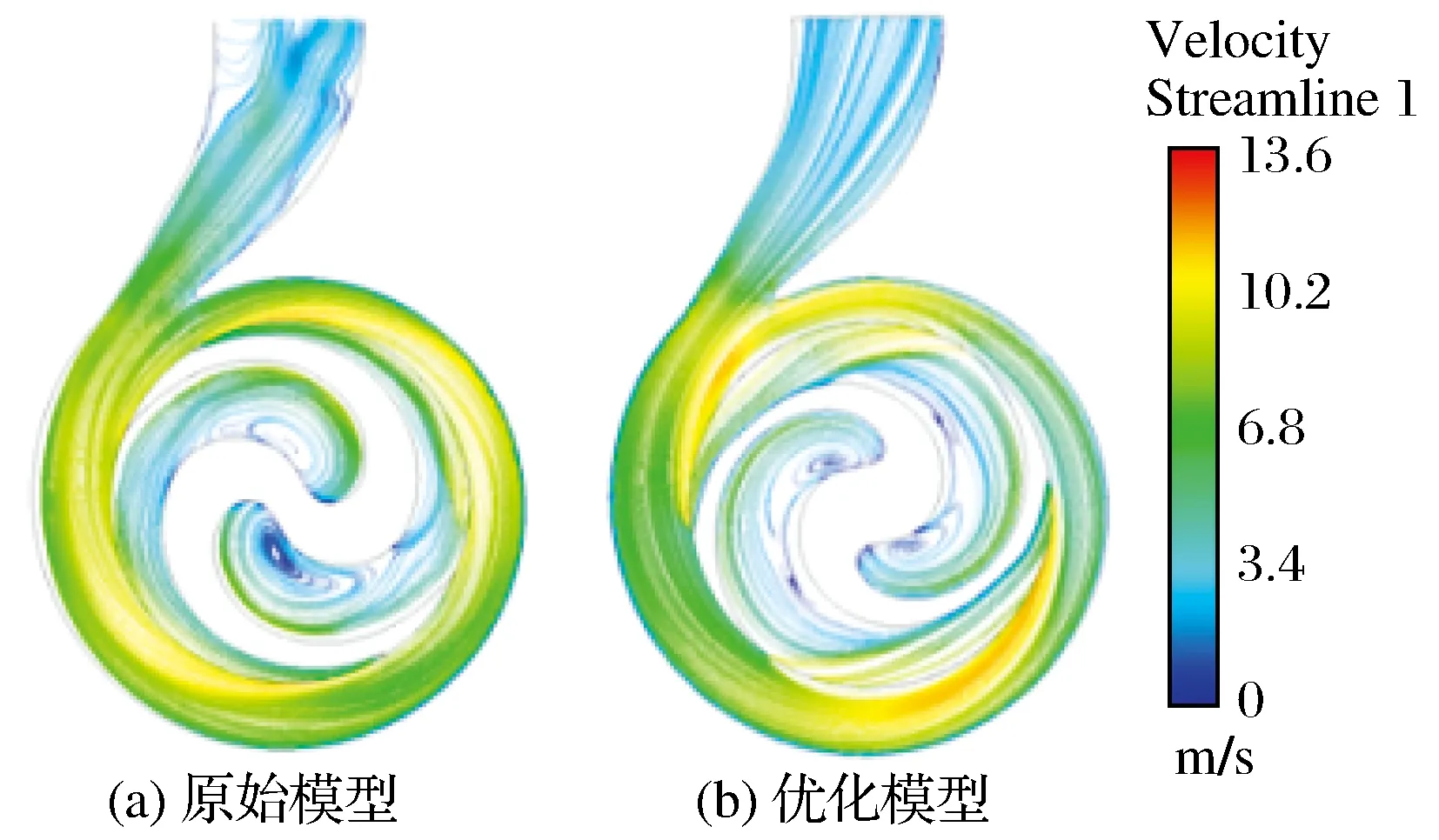
图8 优化前后中间截面流线分布Fig.8 Streamline distribution on middle section of pump before and after optimization
优化前后蜗壳中的水力损失对比如图9所示。水力损失计算公式为
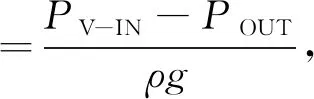
(2)
其中:POUT为泵出口压力(Pa);PV-IN为蜗壳进口压力(Pa);ρ为液体密度(kg/m3);g为重力加速(m/s2)。由图9可知,当Qd>9m3/h时优化模型蜗壳中的水力损失均小于原始模型的水力损失。原始模型蜗壳中的水力损失随着流量的增加而增大,优化后,蜗壳中的水力损失随着流量的增加先减小后增大,在额定工况点,水力损失最小。综合优化前后水泵的性能曲线及额定工况下泵内的流态可知,蜗壳内液体的流态对水力性能的改善有显著影响。
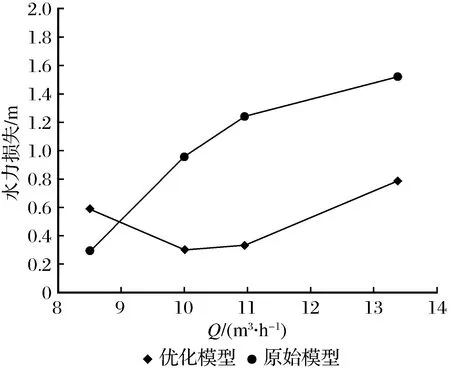
图9 蜗壳中水力损失对比曲线Fig.9 Comparison of model pump hydraulic loss
5 结论
基于正交试验、CFD数值计算与试验相结合的方法,对一台双流道泵叶轮进行优化设计,得到以下结论:
(1) 原始模型数值模拟与试验外特性曲线趋势基本一致,符合工程实际,说明该数值模拟方法可行。
(2) 流道中线的变化对双流道泵的水力性能有影响,通过极差分析可以看出,在选择的4个因素中,包角Ψ对扬程影响最大,后盖板圆弧R2对效率的影响最大。
(3) 利用正交试验设计计算方案,通过CFD预测了泵在设计工况点运行时的性能,经极差分析后找到了最优的设计方案,其参数组合为R1=20,R2=51,Ψ=200°,m=0.85。额定工况下,优化后泵的扬程较原始模型提高0.59m、效率提高了5.4%,改善了蜗壳中的流态。
