融通与思辨：HPM 视域下数学化思维的探索与实践

苏龙霞

HPM（History and Pedagogy of Mathematics）指的是数学史与数学教育。华东师范大学汪晓勤教授研究团队指出，在数学教学中融入数学史有六大价值——知识之谐、方法之美、探究之乐、能力之助、文化之魅、德育之效。这些足可见融入数学史的数学教学对学生数学学习特别是数学思维的影响。数学思维（数学化思维）即“人类对数学的认识过程，是大脑不断反映转化的过程， 是人们从事数学活动 （一般指研究数学、学习数学、应用数学和讲授数学的活动） 中的理性认识过程， 是人们形成数学思维形式、数学概念、数学命题、数学推理和数学理论的思维过程”。有学习就有思维的参与。南京大学郑毓信教授认为，“只有帮助学生数学化的思维，才能更深刻体现数学史融入教学的意义，才能真正从‘冰冷的美丽’到‘火热的思考’”“教师应通过数学教学帮助学生改进思维，达到数学化的思维”。根据数学史融入数学教学的四种基本方式，教师应更好地引导和帮助学生进行数学化思维，真正实现学生核心素养的提升。

一、附加式融入——引趣与导思

数学的发展是一部充满曲折和智慧的历史，每一个数学知识的背后都印记着先哲们的努力与奋斗，在其发现探究过程中，本身就附带着一个个迷人的故事，这些故事、人物、史实应在适当的时机分享给学生，也就是附加式融入的数学史教学方式。附加式融入就是利用图片、语言和视频等方式，以外部介绍传输的形式传递给学生数学史知识，使学生体会“在数学里，有美不胜收的故事；在故事里，有美不胜收的数学”。附加式融入的主要特点是把数学史作为课堂教学的一个有益补充，课堂中这些与内容相关的、有意义的数学故事，不仅可以激发学生的学习兴趣，还可以使数学富有人文色彩，激发学生的兴趣，启发思考。

翻看人教版数学教材，在“你知道吗”栏目中有许多数学史的介绍，这些内容可以采用以附加式融入为主的方式进行教学。还有一些与数学有关的名言、数学家的故事、数学概念、数学术语、数学符号等趣味横生的资源也可同时融入。如学习“位置与方向”时，教师可引入“笛卡尔病床上苍蝇位置标示”的故事；在学习“大数的认识”时，教师可讲述“阿基米德数沙粒”的传说；在学习“圆面积”时，教师可引入开普勒的故事。再如，教师还可适时引入古希腊毕达哥拉斯的“完美数”，笛卡尔的“爱情表达式”，“站在巨人肩膀”的牛顿，“数学界的莎士比亚”欧拉，等等。这些都可促使学生产生美好遐想，激发数学兴趣，同时促使他们产生“怎么会那样”等疑问，从而产生进一步探究为什么的兴趣。

例如，“年月日”的教学中，教师就可以以附加式融入为主的方式融入数学史料。在了解学生“关于年月日知道了什么”的认知起点的基础上，教师可用视频等形式引入年月日的来历以及年月日的产生与太阳、月亮、地球公转及自转的关系，还有因而引发的月圆月缺的故事。古人是从先熟悉日到月再到年的，学生学习的顺序也是“日、月、年”，这与人类的生活性、自然性是吻合的。同时，教师还要引导学生建立度量单位学习的结构，即从大到小再到更小的认知过程，要引发学生思考“凯撒和奥古斯是怎么动日历的？”“大月小月平月是怎么来的？”“你会自己制作日历吗？”等，使学生在链接历史中丰富认知，啟迪思考。

二、复制式融入——体验与感悟

数学发展历史中有许多关于名题和热议问题的解答与争论，其中发生的故事更是不胜枚举。教学中，教师针对对应的知识直接呈现历史上曾出现的数学问题或者数学解法，这就是复制式融入。复制式融入是让学生在与先哲的对话中，找寻解题的方法和规律，感悟历史的探索过程，体会历史的沉淀。复制式融入运用方式的特点是直接采用。学生必须去解读古语所传达的信息，转化成现代的数学语言，再经历分析比较等思维过程，对比中感悟古人的解答智慧，提升数学素养。

数学教材上也有很多可以利用复制式融入进行数学史相关教学的内容（如表1）。历史上的名题往往也可以采用这种方法，如人教版数学教材四年级下册的“鸡兔同笼”问题即是直接的复制式采用。再如，学习行程问题时，也可以直接采用《计算之书》中的两船相遇问题。而在学习两位数乘法时，还可以采用古代格子算法等，努力实现学生的体验感悟，促使其更深刻地进行思考。

在学习“鸡兔问题”时，出示古题之后，教师可以让学生先自由解读，理解题意，然后独立思考怎么解答。在学生陆续得到表格法、画图法、假设法等方法并交流其异同与联系后，教师可先对比《孙子算经》的算法，将所有动物的脚数除以2，也就是94÷2=47。每只鸡有一对脚，兔子有两对脚。然后，假设所有的动物都是鸡的话，就应该有35对脚，但事实上有47对脚。如果将一只鸡换成一只兔子的话，用47减去35，得到12，说明需要有12只鸡被换成兔子，这就是兔子的数目。最后，引导学生思考：“为什么可以这样解答？”学生将很容易就能得到其实际上是假设法的运用。在此基础上，教师还可以介绍古人的其他想法——抬腿法、吹哨法、砍足法等，使学生在一一对比中，升华认识，感悟成长。

三、顺应式融入——探究与思辨

数学发展源远流长，有些材料经过适当编制或根据数学问题进行改编，会成为很好的学习素材，从而体现“古为今用、推陈出新”，这就是顺应式融入。顺应式融入的主要特点是根据课堂教学的需求对原始文献进行改编，这类材料从表面上看已经没有了历史的痕迹，但它们既传承了历史的精神，又顺应了时代的要求，还在仿真对比中使学生学会求知，发展思维。

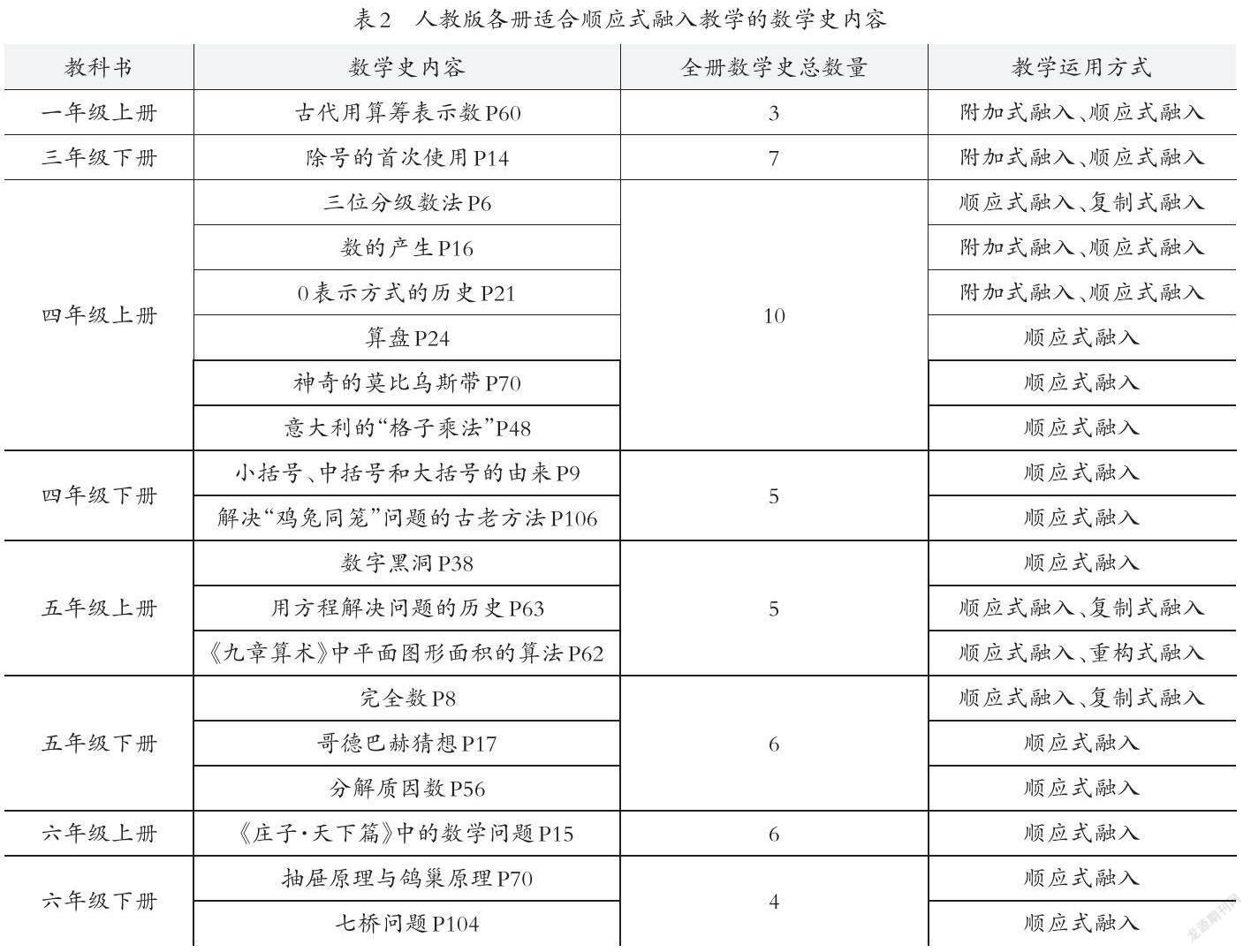
顺应式融入适用于跟历史上方法近似、情境相同或知识点一样的素材使用，可以根据材料创编为新课的例题，也可以改编问题为练习题用，或在方法的推介上运用。如表2的列举即教材中适合使用顺应式融入的数学史内容。

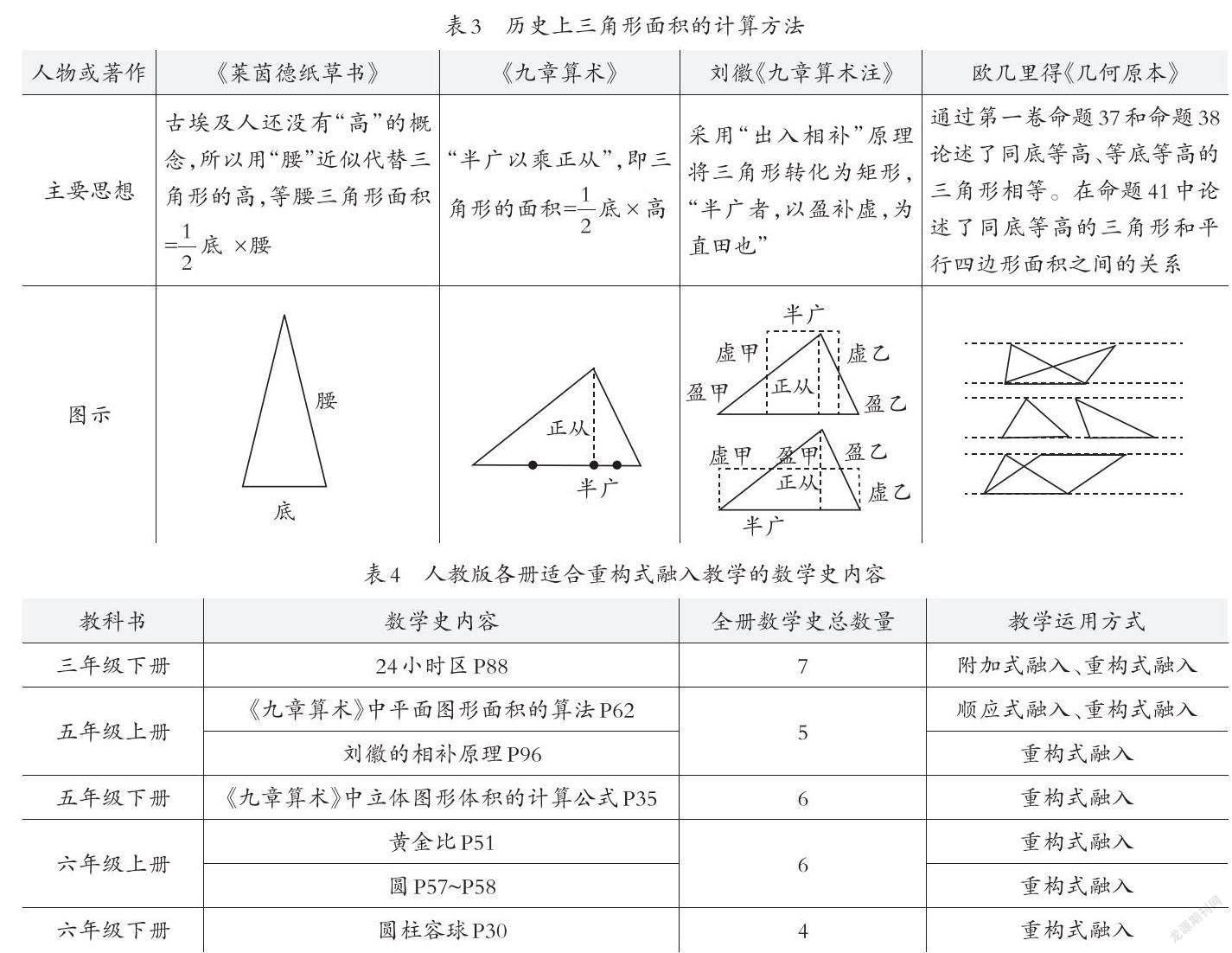
在学习“三角形面积”时，教师应引导学生了解面积的历史并借鉴历史上三角形面积的计算方法（如下页表3）。面积计算的产生源于生活生产的需要，因为尼罗河河水的泛滥，造成土地面积划分困难，因此才有面积计算的需求。创设这样的情境导入，加上出示一组平行线间两个规范的平行四边形和三角形（改编于《几何原本》），可激发学生对计算学习的需求，也可使他们联想到应用数学解决生活实际问题——“要想知道它们的面积，需要测量什么？”进而在得出倍比法的同时对比割补法以及对古人方法的评价与分析。“比较分类就是一种有效的思维过程”，通过仿真比较，能更好地促使学生反思，实现其思维的成长。

四、重构式融入——建构与融通

历史相似性告诉我们，学生在学习中碰到的困难往往就是数学家们当时遇到的困难。在数学学习过程中，借鉴或者重构知识最原始的发生、发展过程，能够将知识所包含的最核心的数学思想、数学方法体现出来，从而呈现出数学知识的自然发生过程。在重演历史中尝试建构知识体系，能真正融通数学史与数学学习的桥梁，提升学生的数学素养。

人教版数学教材在“你知道吗”“数学广角”等板块都有专门的数学史内容，而且都是配合本单元相关学习的内容有序、成体系的安排。结合相关内容（如下页表4）的学习，教师可以以重构式融入的方法为主组织教学。在重构式融入教学中，学生将在真实情境中获得“古为今用”的美好体会，不仅体现了历史发生法，更使学生通过探究和不断调整，建构自己的知识体系，发展数学素养。

度量的发展史，是从抽象的单位如几个、几头、几种等到利用工具得到实质测量。最初的距离测量都是用人身体上的器官作为测量工具的，如“拃”（尺）、“咫”（成年女人大拇指与中指之间的距离）等。而“英尺”的界定，则是16世纪的德国人在某礼拜日把从教堂里走出的16个成年男子集中在一起，测量每人左脚的长度、加在一起取平均值来定义的，这个通过平均值来得到的长度一直延续使用至今。为此，在设计测量教学时，就可以重构历史的镜头，“你在一个关闭的只有一扇门和一个窗的房间里，又没有任何可以参照的前提下，怎么告诉别人窗有多高，门有多宽？”从而引发学生思考：可以用手臂长、两脚张开的长等来大约说出其宽和高。在这个过程中，学生经历了古人的困境，学会了分析、辩证，最终建构起度量最本质的特征——测量单位的确定与累积，从而也融通了古今对照。

当然，我们应该清楚数学史融入数学教学，不是只有单一的融入方式，也不是只有教材上所呈现的显性的数学史内容，而更重要的是“为教育的历史”“数学史是教学的指南”的意识与观念。在实际教学中，我们应该针对不同教材内容的不同知识特征，收集更多的数学史材料，寻找更多灵活搭配融通的运用方式。只有这样，才能真正实现“智力教育是数学教学的重要使命”，实现学生数学化的思维和核心素养的发展。

课题项目：1. 本文系福建省教育科学“十三五”规劃2020年度课题“HPM视角下运用数学史提升学生推理素养的教学实践研究”研究成果。课题编号：FJJKXB20-553。2. 本文系福建省教育科学“十三五”规划2016年度课题“小学数学思·辩课堂的探索与实践”研究成果。课题编号：FJJKXB16-224。

（责任编辑：杨强）