一种稀疏重建的天波雷达射频干扰抑制算法*

邱 峰，黄中华，邹欣颖

(1.航空工业第一飞机设计研究院，西安 710089；2.中国人民解放军93129部队，北京 100843；3.电子科技大学 信息与通信工程学院，成都 611731)

0 引 言

天波雷达工作在短波频段(330 MHz)，该频段也正好是各种短波通信和广播电台信号的工作频段[1-2]。这些通信和广播电台信号单程传播到雷达接收机，会形成很强的射频干扰，掩盖目标回波信号，从而使得雷达无法探测目标，因而射频干扰抑制受到了广泛关注[3]。

目前的射频干扰抑制方法主要可分成三类。第一类是利用目标回波信号和射频干扰的空间方向不同，用空域滤波方法抑制射频干扰[4-6]。然而，该方法难以抑制主瓣内的射频干扰。第二类是匹配滤波之后的射频干扰抑制方法[7-9]。该方法首先进行匹配滤波，将信号转换到距离多普勒域，然后利用射频干扰在距离维具有强相关的特点来抑制射频干扰。该方法可有效抑制主瓣内的射频干扰的抑制，然而在匹配滤波处理之后，射频干扰和目标信号较难区分，因此该方法容易影响到目标信号。第三类是基于相似约束的射频干扰抑制方法[10-13]。该方法将射频干扰抑制与匹配滤波进行综合设计，通过相似约束使滤波器逼近匹配滤波的性能，并通过最大化输出信干噪比(Signal-to-Interference plus Noise Ratio,SINR) 实现匹配滤波和干扰抑制。该方法可以有效抑制主瓣内的射频干扰，并且不影响目标信号，因而受到了广泛关注。

本文注意到，从频域看，上述基于相似约束的射频干扰抑制方法可看作是在匹配滤波器的基础上叠加一个窄带滤波器，并且窄带滤波器具有稀疏特性，对窄带滤波器施加稀疏性约束并加大对稀疏项的惩罚能够更彻底地抑制干扰[14-15]。基于该特点，本文提出了一种稀疏约束的射频干扰抑制方法。实测数据的处理结果表明，本文所提算法能够有效抑制射频干扰，输出SINR比文献[10-12]中的方法提高了1 dB以上。

1 问题描述

假设雷达接收阵列有M个阵元，雷达发射信号是s，则天波雷达接收信号x∈M×1是

x=μs+i+n。

(1)

式中：μs是目标回波，μ表示目标回波的强度与多普勒频移；i是射频干扰；n是噪声。

传统的匹配滤波方法无法抑制射频干扰。为了解决该问题，文献[10-13]提出了基于相似约束的射频干扰抑制方法。该方法对滤波器权向量w施加恒模约束和相似约束，建模得到如下优化问题：

(2a)

s.t. ‖w‖2=1,‖w-s‖2≤ε0。

(2b)

式中：R=E[(i+n)(i+n)H]是干扰加噪声的协方差矩阵；‖·‖表示欧几里得范数；ε0(通常情况下，0<ε0≤1)为相似度参数，用以控制滤波器向量和发射信号之间的相似度。求解出w后，对雷达接收的信号用w滤波，就可以同时实匹配滤波和射频干扰抑制。

2 所提方法

本节提出了基于稀疏相似约束的射频干扰抑制算法。该算法基于最大化输出SINR的准则，对窄带滤波施加稀疏约束，并利用交替性自适应迭代算法求解，实现在匹配滤波的同时有效抑制射频干扰。

2.1 分解射频干扰滤波器

本节在频域分析的基础上，将文献[10-11]中的相似约束的射频干扰抑制滤波器分解为匹配滤波器加窄带滤波器，相较于相似约束的设计方法直接求解的方法大大提高了射频射频干扰抑制滤波器的设计自由度，为后面设计稀疏相似约束的射频干扰抑制方法提供了基础。

从频域上看，雷达接收的信号可看作目标回波和射频干扰之和。假设天波雷达发射信号为线性调频信号，则目标回波信号也是线性调频信号。射频干扰通常是短波通信信号或者广播电台信号，该信号可近似看作单频信号。于是，雷达接收信号的频谱示意图如图1所示。

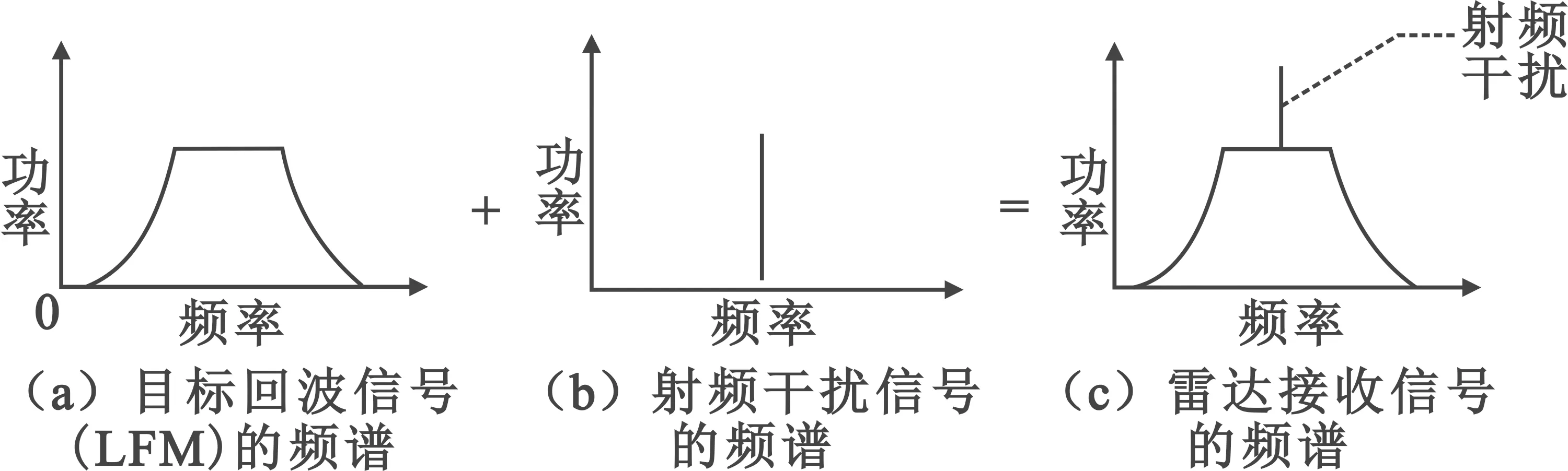
图1 信号频谱分析图

匹配滤波器的系数为wMF=s。由匹配滤波器原理可知，匹配滤波器是一种输出信噪比最大的滤波器。根据匹配滤波器原理，在时域上，是卷积运算；在频域上，匹配滤波是发射信号的频谱与接收信号的频谱做乘积运算。于是，优化问题(2) 中，‖w-s‖2≤ε0表示设计的滤波器w要尽量逼近匹配滤波器wMF=s，minwHRw则表示设计的滤波器要使得滤波后的总能量最小，也就是要尽量抑制射频干扰。结合图1可以看出，优化问题(2)所设计的滤波器实际上是在匹配滤波器上对应于射频干扰的频点上形成一个凹口，如图2所示。因此，文献[10-11]设计的基于相似约束的射频干扰滤波器可表示为图2(a)，该滤波器可分拆为匹配滤波器(图2(b))加上窄带滤波器(图2(c))。

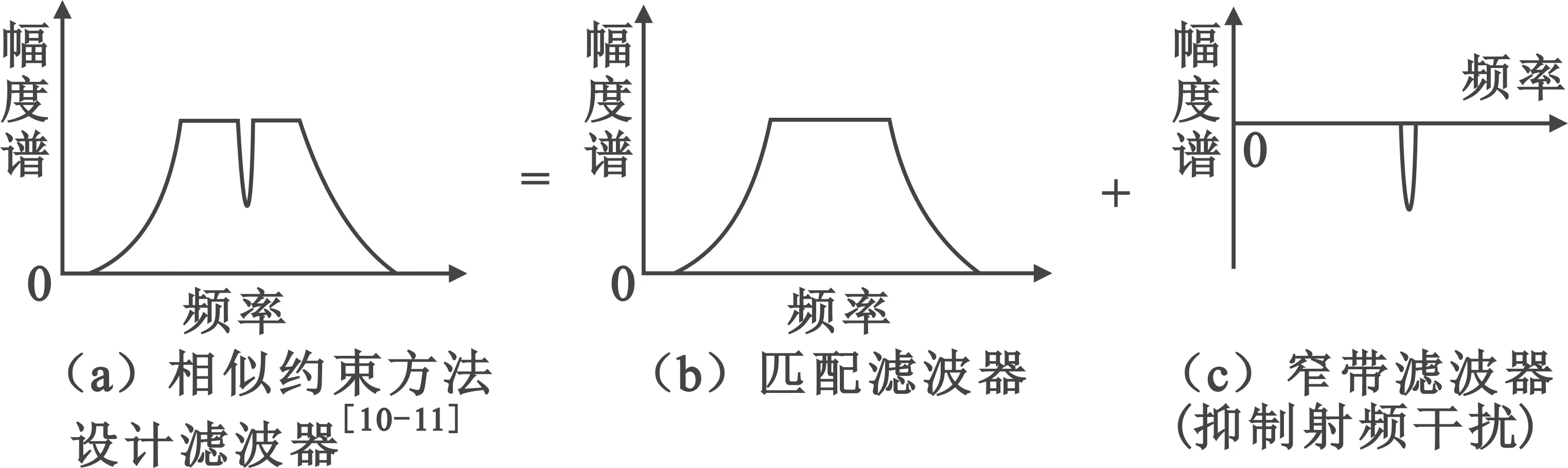
图2 相似约束的射频干扰抑制滤波器分解示意图

2.2 所提的稀疏重建的射频干扰抑制方法

根据2.1节的分析，文献[10-11]中基于相似约束的滤波器可拆分为w=s+x，其中，s为匹配滤波器，x为窄带滤波器。进一步注意到，窄带滤波器x具有稀疏性。

基于上述分析，首先将基于相似约束的射频干扰抑制滤波器分解成匹配滤波器加窄带滤波器，并在此基础上对窄带滤波器施加稀疏约束，于是得到如下优化模型：

(3a)

s.t. ‖s+x‖2=1,‖(s+x)-s‖2<ε。

(3b)

式中：ε(0<ε≤1)为相似度参数；‖·‖1表示l1范数；‖x‖1为稀疏项。

公式(3)是多约束非凸优化问题，适合用交替迭代方法求得全局最优解。于是，公式(3)的优化问题可改写为

(4a)

(4b)

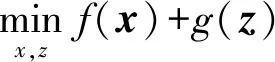
(5a)

s.t.x-z=0 ，

(5b)

‖s+x‖2=1 ，

(5c)

(5d)

式中：Re(·)表示取实部。

引入对偶变量v，公式(5)的惩罚函数为

(6a)

s.t. ‖s+x‖2=1，

(6b)

(6c)

(7a)

s.t. ‖s+x‖2=1，

(7b)

(7c)

利用自适应交替乘子法对公式(7)进行迭代求解，则所提方法的第i+1次迭代求解如下：

(8a)

(8b)

(9)

ui+1=ui+xi+1-zi+1。

(10)

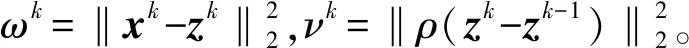
接下来，将分别求解公式(8a)中的xi+1和公式(9)中的zi+1。

(1)求解公式(8a)更新xi+1

由于w=s+x，所以，公式(8a)可写为

实验中分别测试在任务数为100、200和400时，不同迭代次数情况下与Cloudsim原有调度算法FIFO、基本PSO算法进行了比较，按照各自算法得到的调度策略进行调度的任务总完成时间，实验结果如图1～3所示．

(11a)

(11b)

那么，代价函数可以改写为

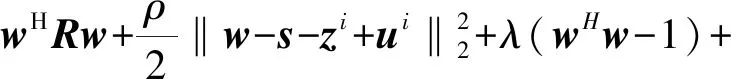
μ(2-ε-wHs-sHw)。

(12)

式中:λ和μ为拉格朗日惩罚参数。对公式(12)化简得到

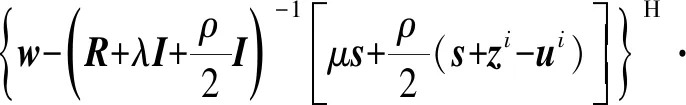
(13)

从公式(13)中可看出，当w的值为

(14)

把式(14)中的wi+1(λ,μ)回代到公式(13)，得到

(15)

公式(15)对μ求导后得到

(16)

将公式(16)代入公式(14)得到滤波向量

(17)

相应地，公式(8a)中xi+1为

(18)

同时满足问题(8)的两个约束条件。

(2)求解公式(9)更新zi+1

对公式(9)进行求解得

(19)

式中：S为阈值运算符，

(20)

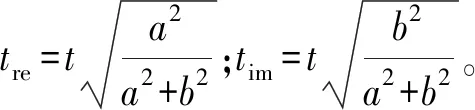
综上所述，基于稀疏相似约束的最优滤波器向量求解过程如下：

Step1 干扰协方差矩阵R，发射波形s，相似度ε0，初始化i=0，w0=0，z0=0，u0=0。

Step2 令i=i+1。

Step2.1 根据公式(14)计算wi。

Step2.2 根据公式(19)更新zi。

Step2.3 根据公式(10)更新ui。

Step3 判断是否收敛，若算法收敛，输出w，否则返回Step 2。

3 实测数据处理和性能仿真

3.1 实测数据处理分析

该实测数据由我国某实验型天波超视距雷达所录取，为雷达接收信号经过去载频后的基带数据，主要针对空中飞行目标检测。天波雷达工作频率为f0=18.3 MHz，发射信号脉冲重复周期T=12 ms，脉冲重复累积个数为M=512，阵元数N=192，相干积累时间6.144 s。两个射频干扰频率分别为6.5 Hz和22 Hz，射频干扰非常接近目标区域，严重影响了目标的识别。

图3分别为文献[18-19]的典型匹配滤波器方法、文献[10-12]的相似约束方法和本文所提方法对实测数据处理后的距离-多普勒图。从图3(a)中可以看出，射频干扰信号经过接收机进行信号处理后，在频域上为一条平行于距离轴的条形带，会对目标回波信号的识别产生干扰，而本文所提方法和相似约束方法设计的滤波器能够滤除条形带谱线，从而有效抑制射频干扰。图3(c)的噪声基底低于图3(b)的噪声基底，表明本文所提算法的干扰抑制性能优于文献[10-12]的相似约束方法。

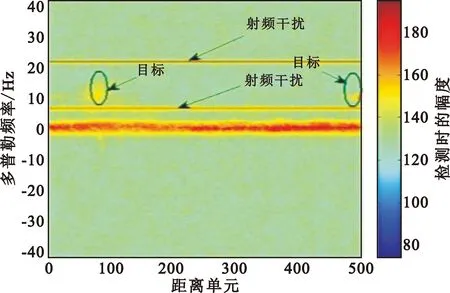
(a)文献[18-19]的匹配滤波器方法

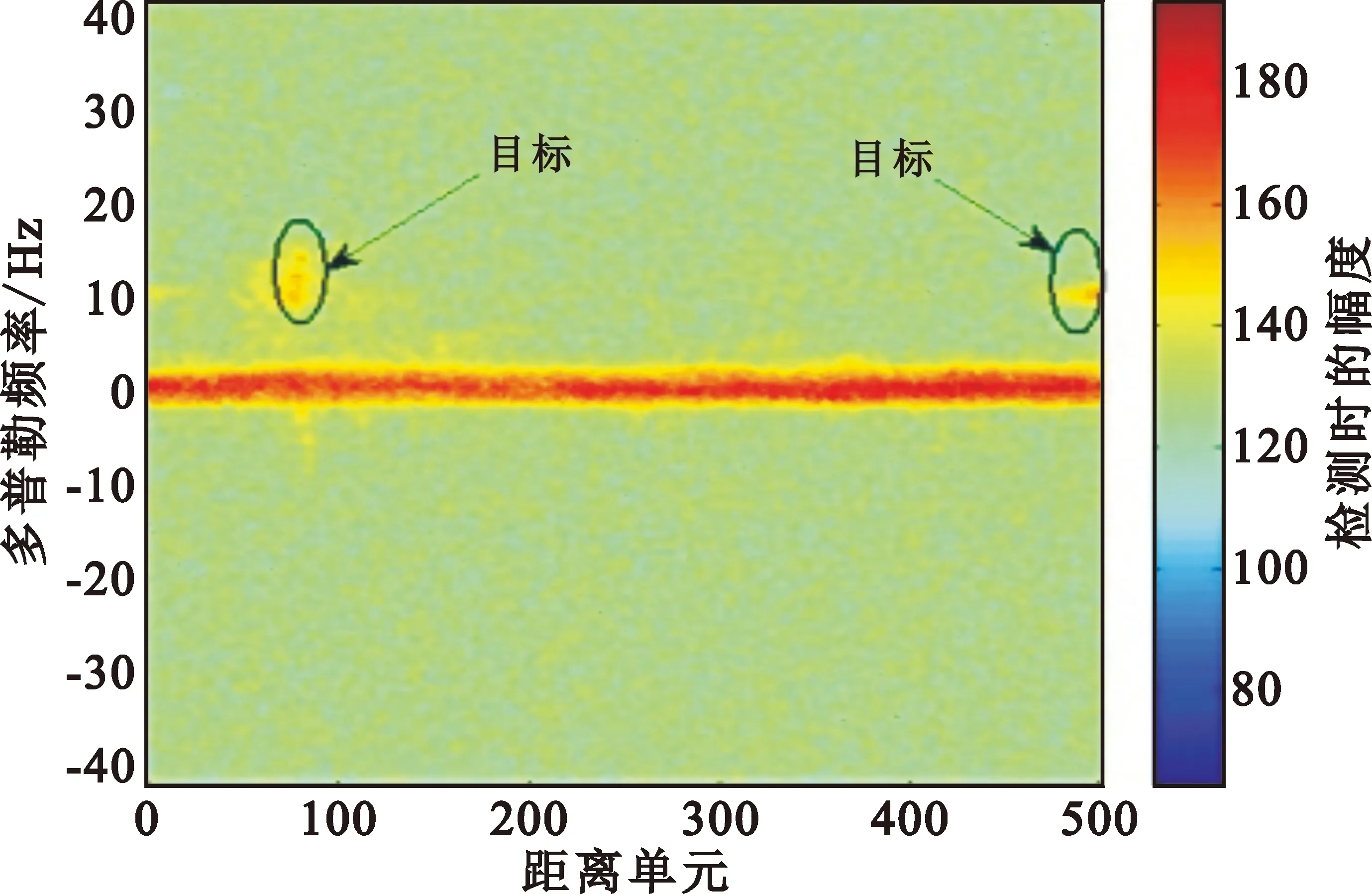
(b)文献[10-12]的相似约束方法

(c)本文所提方法图3 射频干扰抑制结果

3.2 仿真性能对比分析

假设回波数据中存在一个频率为-5.833 Hz、功率为19.71 dB的单频射频干扰信号，雷达接收回波的频谱如图4所示。

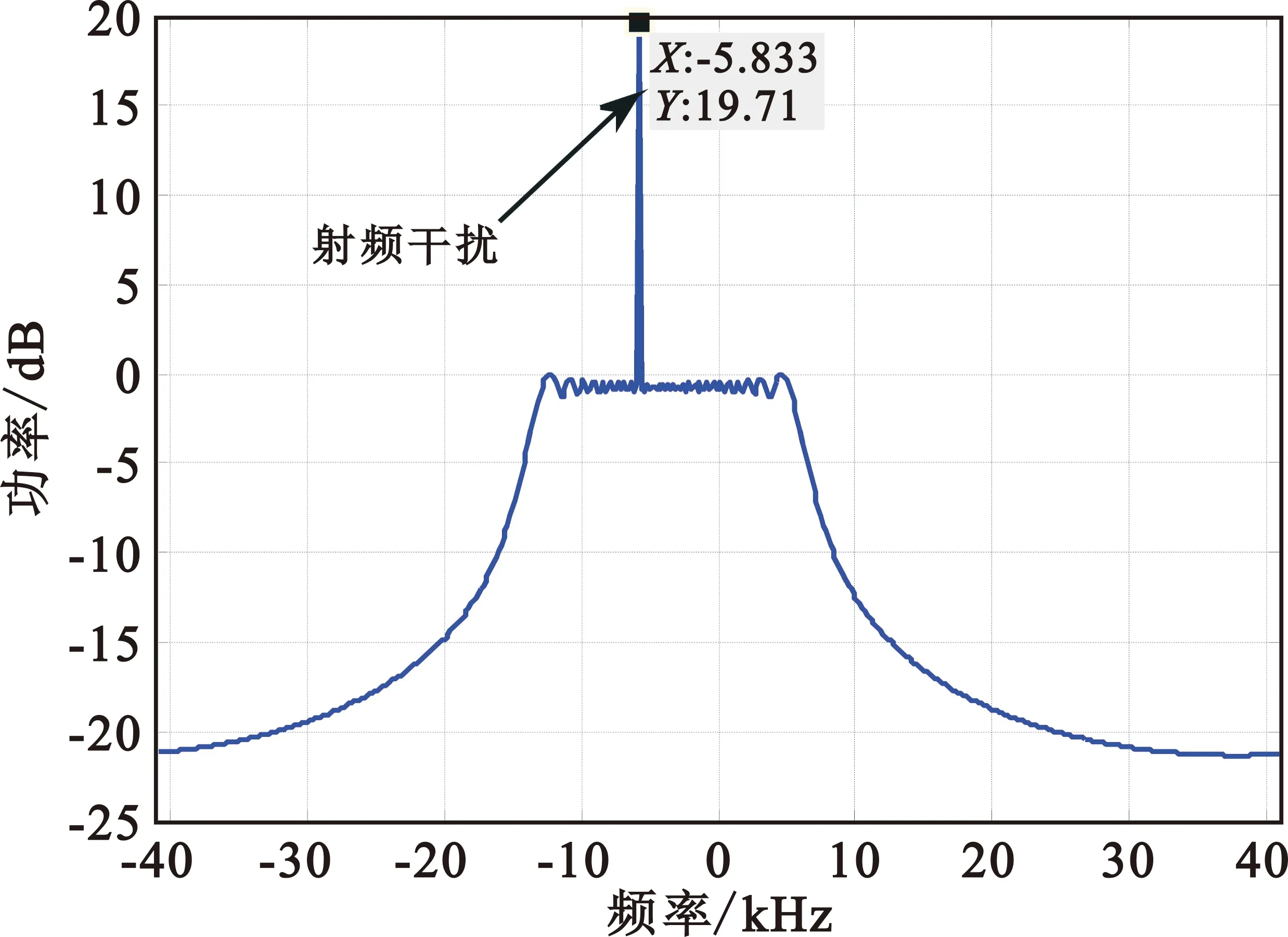
图4 接收信号频谱图

针对图4的接收信号频谱图，分别采用文献[18-19]的匹配滤波器方法、文献[10-12]的相似约束方法与本文所提方法设计抑制射频干扰匹配滤波器，得到的滤波器频谱图如图5所示。从图5中可看出，基于相似约束的滤波器频谱在频谱范围内有明显的振荡，降低了雷达系统输出的SINR，而本文所提算法的滤波器频谱较为光滑，更接近理想的匹配滤波器的频谱，因此能获得更优的射频干扰抑制和匹配滤波效果。

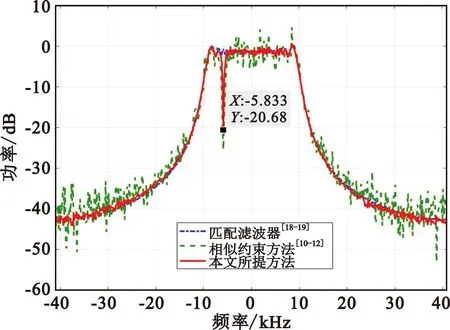
图5 滤波器频谱图

图6为相似约束方法[10-12]和本文所提方法的输入-输出信干噪比变化曲线。从图中可明显看到，使用本文所提方法比使用相似约束方法得到的输出信干噪比提高了1 dB。

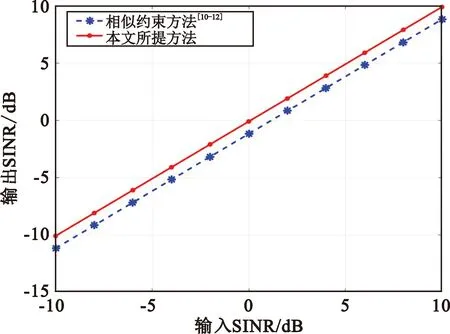
图6 输入-输出信干噪比图

4 结 论

本文针对天波雷达的射频干扰抑制进行研究。首先将基于相似约束的射频干扰抑制滤波器分解为匹配滤波器和窄带滤波器， 并进一步注意到窄带滤波器具有稀疏性。在此基础上，提出了基于稀疏相似约束的射频干扰抑制算法，充分利用窄带滤波器具有稀疏性的先验知识来提高射频干扰信号抑制性能。仿真结果表明，所提方法的输出SINR较基于相似约束算法高1 dB，有效地提高了射频干扰抑制性能。