利用部分重叠信道的多无人机自主协同优化抗干扰*

姚昌华，程 康，张建照，刘 鑫，胡程程

(1.南京信息工程大学 电子与信息工程学院,南京 210044；2.国防科技大学第六十三研究所,南京 210007；3.桂林理工大学 信息科学与工程学院,广西 桂林 541007)

0 引 言

近年来，无人机技术发展迅猛，成本低、灵活和反应迅速的优点使得无人机应用在军事、交通和农业等多个领域，其中多无人机协同技术更是备受关注。多无人机协同技术是人们根据自然界中蜂群和鱼群等生物行为模仿得到的。多无人机协同技术通过协同作战、共享信息和分工合作完成目标任务[1]，实现群体利益最大化。然而，多无人机通信网络容易受到恶意干扰，导致无人机的通信数据缺失、中断，因此多无人机通信网络的抗干扰问题是亟待解决的问题。

在多无人机通信网络场景中，无人机的目标是实现最优信息传输速率，干扰机的目标是实现干扰效果最大化。因此，考虑到无人机和干扰机的决策分层结构，博弈论是解决多无人机通信网络抗干扰问题的主流方法之一。针对不同用户之间的相互干扰问题，文献[2]提出了一种MAC层干扰博弈模型，实现了用户之间干扰的最小化。针对通信网络中干扰环境下的分布式信道分配问题，文献[3]提出了一种非合作博弈的方法，实现了最优信道资源分配。针对认知无线网络中用户控制信道被干扰问题，文献[4]提出了一种随机博弈的方法，实现了动态信道变化和不完全感知的情况下减弱干扰的效果。

部分研究采用Stackelberg博弈模型解决抗干扰问题。针对多无人机通信网络中不完全信息下功率控制问题，文献[5]提出了基于Bayesian-Stackelberg博弈的抗干扰模型，实现了博弈双方获得最佳传输功率。针对多无人机通信网络中的同频互扰和恶意干扰问题，文献[6]提出了基于Stackelberg博弈的抗干扰模型，利用对偶优化理论，优化博弈双方的传输功率，提高多无人机通信网络性能。

然而，上述文献的研究重点是同信道抗干扰场景，主要关注干扰机对无人机的恶意干扰。针对多无人机通信网络中相互干扰与信息交换成本之间的关系问题，文献[7]利用部分重叠信道的特性,提出了双向共识博弈的模型，从而最大化多无人机通信网络的效用。针对具有部分重叠信道的机会频谱接入问题，文献[8]利用博弈论证明了部分重叠信道可以提高频率利用率，减轻干扰，提高通信网络吞吐量。

综上所述，对于同信道抗干扰场景，利用博弈论优化用户传输参数，确保多无人机通信网络的性能的研究已经取得较多成果，但同信道抗干扰场景的应用范围具有单一性和局限性。因此，本文研究了多无人机通信网络抗干扰中的传输功率和信道联合优化问题，利用部分重叠信道的特性，优化多无人机通信网络的抗干扰性能。考虑多无人机通信网络面临外部恶意干扰、用户间互扰，以及与部分重叠信道切换问题，构建了利用部分重叠信道条件下进行信道和功率联合选择优化的Stackelberg博弈抗干扰模型；对博弈参与者设计不同的效用函数，利用凸优化与对偶理论证明所提博弈具有唯一博弈均衡解，并提出了基于次梯度迭代的算法求解博弈均衡解，获得无人机用户在干扰条件下的部分重叠信道选择和功率优化解。通过仿真对比分析了用户与干扰机在同信道、部分重叠信道场景下功率收敛值，不同数量用户对多无人机通信网络抗干扰性能的影响，以及信道增益和干扰增益等参数对收敛功率值的影响。

1 系统模型和问题建模

1.1 多无人机通信网络抗干扰系统模型

在多无人机通信网络中存在3个无人机用户和1个干扰机，其中每个无人机用户包括1个发送端无人机和1个接收端无人机。如图1所示，无人机用户和干扰机起初在相同信道工作，通过博弈对抗，无人机用户和干扰机获得最优的工作功率。功率较大的无人机用户i为获得更高的传输效用，切换到部分重叠2信道躲避干扰机的干扰效果。

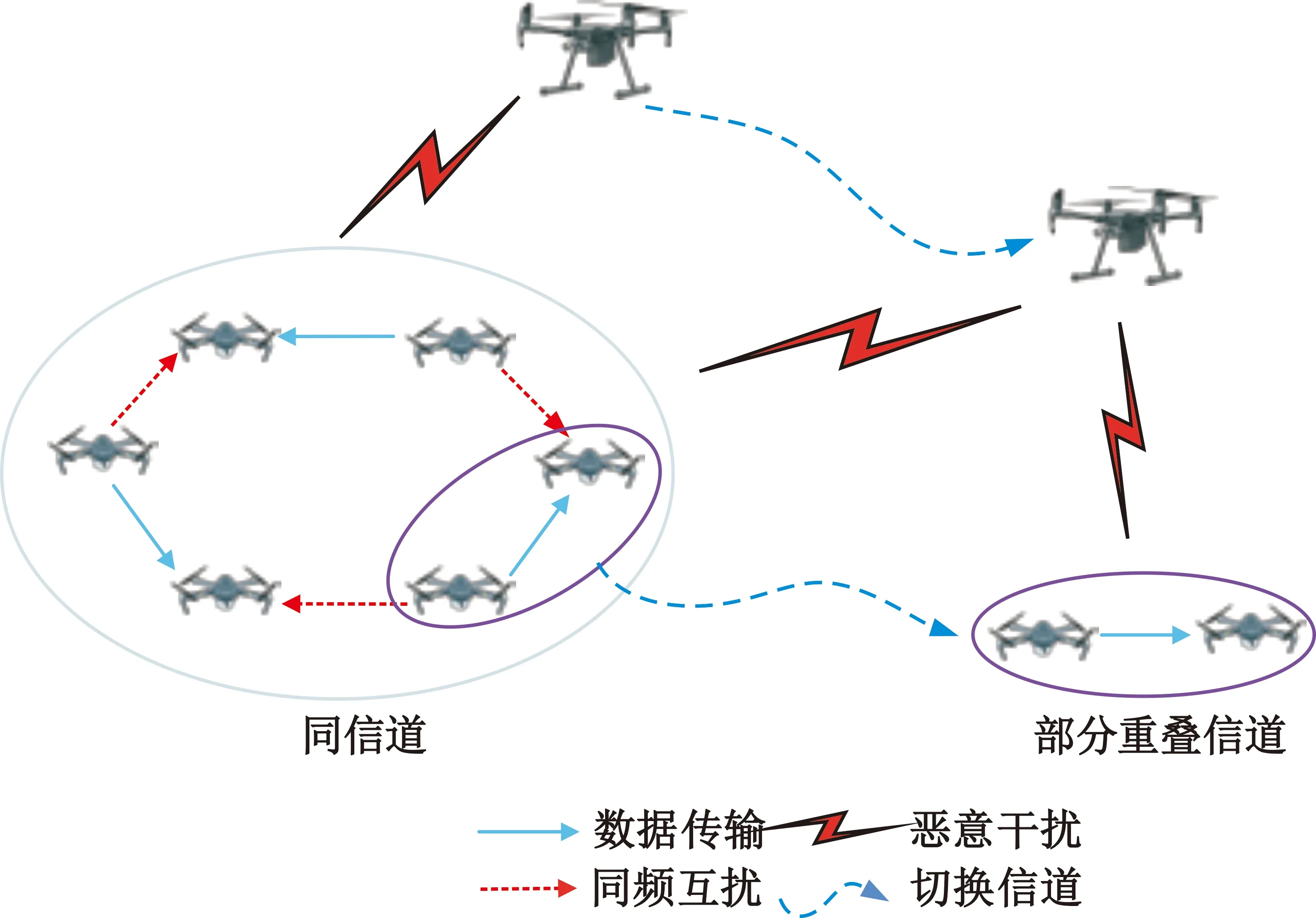
图1 多无人机通信网络抗干扰模型

对于干扰机而言，它能感知无人机用户的动态，跟踪无人机用户i切换到部分重叠2信道并且同时发射干扰信号干扰1信道的无人机用户，动态调整攻击策略，实现对无人机用户破坏效果最大化。对于无人机用户而言，动态调整无人机用户的抗干扰策略，确保整个无人机群通信网络性能。

为了提高多无人机通信网络的频谱利用效率，采用如图2所示的部分重叠信道。在IEEE 802.11b频带中提供11个部分重叠的信道，信道1、6和11互不重叠(正交)。常见的无线通信网络采用非重叠信道，即正交信道，以避免相邻信道中频谱泄露造成的相互干扰。然而，文献[8]认为用户的发送机与接收机可以在部分重叠信道进行通信；同时文献[9]与文献[10]认为部分重叠信道可以减弱通信干扰、提高频谱利用率并优化网络吞吐量。因此，利用部分重叠信道减少同信道干扰机带来的恶意干扰是可行的。

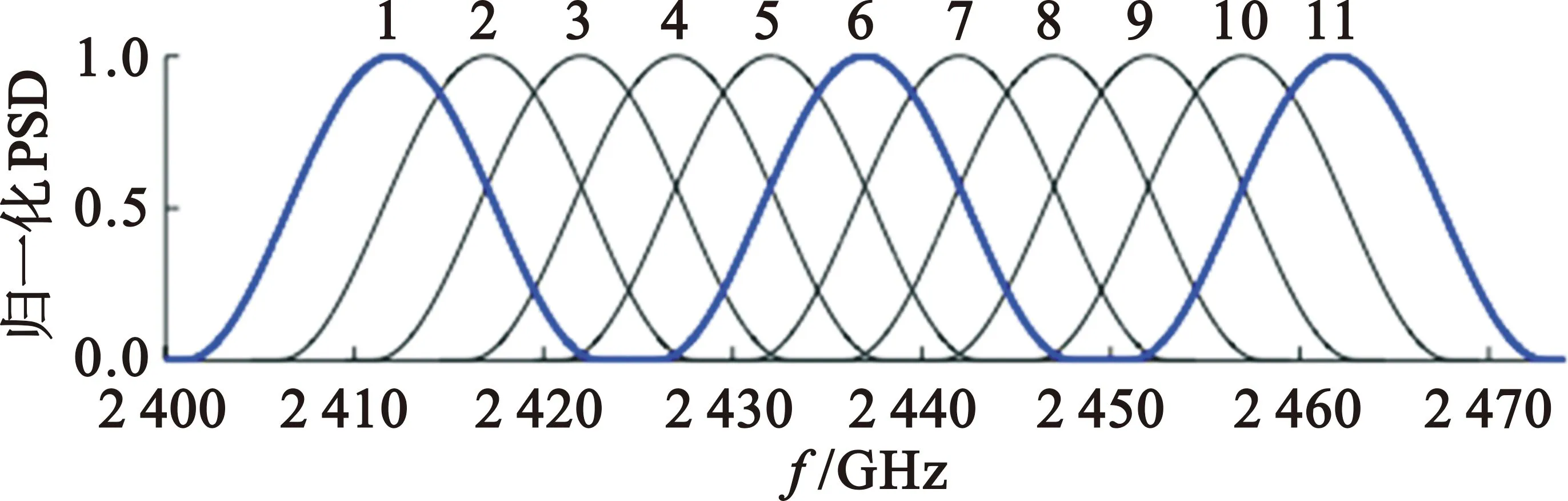
图2 802.11b频带中分布的信道

由于相邻信道存在重叠部分会对接收机接收数据造成干扰，根据文献[11]，重叠程度可以用干扰因子H(δni)表述：

(1)

式中：n,i表示用户或干扰机所处的信道；δni表示用户之间的信道差数或干扰机与用户之间的信道差数。

1.2 问题建模

根据文献[12]与文献[13]可知Stackelberg博弈具有分层特性，对无人机用户和干扰机设计效用函数，同时考虑同频互扰和恶意干扰。首先就用户而言，它的目标是通过抗干扰策略实现传输效用最大化。无人机用户i(i=1,2,…,n)的效用函数表示为

EiPi-ζidiPi-diN。

(2)

式中：B表示信道带宽；αi表示无人机用户i发送机到接收机的信道增益；β表示干扰机对无人机用户i接收机的干扰增益；θm表示无人机用户m对无人机用户i接收机的同频互扰系数；N0表示信道噪声功率；Ei和ζi分别表示无人机用户i的传输代价与切换信道代价；di表示无人机用户i切换信道后与之前信道的间隔;ui和v分别表示无人机用户i与干扰机的信道位置；N表示无人机用户i探寻相邻信道消耗的能量。

对于干扰机而言，它的目标是实现对无人机用户的干扰效果最大化。因此，考虑干扰机在干扰过程中的传输代价与切换信道代价，干扰机的效用函数表示为

CJ-ζdJ-M。

(3)

式中：求和公式表示所有无人机用户的总传输信息量，在公式前增加负号表示干扰机的干扰效果；C与ζ分别表示干扰机的传输代价与切换代价；d表示干扰机切换信道后与之前信道的间隔；M表示干扰机探寻无人机用户时消耗的能量。

此外，为了能更好地体现无线通信系统的性能变化，设置了系统效用函数W：

(4)

2 抗干扰博弈优化分析

本节采用Stackelberg博弈对多无人机通信网络抗干扰进行分析。假设博弈的领导者是干扰机，优先干扰行动，而作为博弈跟随者的无人机用户随后采取抗干扰策略，在多次迭代后，领导者博弈和跟随者博弈达到纳什均衡解。图3是Stackelberg博弈过程示意图，为避免求解Stackelberg均衡解过于复杂，分析过程中使用3个无人机用户，采用逆向递推法分析，先分析跟随者博弈，再分析领导者博弈。

图3 Stackelberg博弈过程

2.1 Stackelberg均衡求解

在Stackelberg博弈中，作为跟随者的无人机用户，通过感知干扰机的干扰策略后，会对自身的传输功率调整，因此，对于无人机用户而言，其优化目标可以表示为

(5)

式中：PM表示无人机用户的最大功率。在博弈过程中，干扰机的干扰功率优先给出，无人机用户i不断对自身功率调整，得出最优传输功率为

(6)

由无人机用户的效用函数可知，Ui是关于Pi的函数且二阶导数小于0，即

(7)

因此，效用函数Ui是关于Pi的凹函数。本节构建拉格朗日函数优化问题，引入约束条件和非负对偶变量λi，将效用函数优化问题认为是凸优化问题。无人机用户i的拉格朗日函数为

EiPi-ζidiPi-diN+λi(PM-Pi) ，

(8)

那么对应的拉格朗日对偶函数可以表示为

(9)

通过文献[14]中的KKT条件

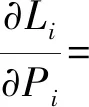
Ei-ζidi-λi

(10)

作为领导者的干扰机优先采取干扰策略，通过博弈对抗，获得干扰机的最优策略。因此，可以确定干扰机的优化目标为

J*=argmaxV(P1(J),…,Pi(J),…,Pn(J),J)
s.t.J≤JM。

(11)

式中：JM表示干扰机的最大功率。通过对跟随者博弈的分析，能确定干扰机的效用函数为

V(P1(J),…,Pi(J),…,Pn(J),J)=

(12)

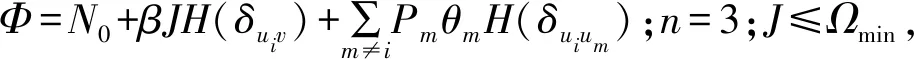
(13)

由公式(14)可知，干扰机的效用函数V是一个关于J的凹函数：

J≤Ωmin,n=3 。

(14)

干扰机的拉格朗日函数为

L(P1(J),…,Pi(J),…,Pn(J),J)=

(15)

通过对干扰机的拉格朗日函数求偏导，令一阶偏导数为零，则

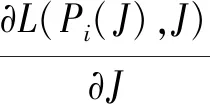
C-ζd-μ。

(16)

最终，能得到干扰机的最优干扰功率

J*=J，

(17)

其中J可由计算机求解。

上面研究了3个无人机用户的场景，下面考虑多无人机通信网络中无人机用户数为n(n≥3)时的情况，总能获得以下最优策略：

(18)

其中，优先获得无人机用户i的最优抗干扰策略Pi(J)，通过Pi(J)能获得干扰机的最优干扰策略J，但J需要满足以下条件：

(19)

式中：i=1,2,3,…,n。

2.2 Stackelberg均衡的存在性和唯一性证明

定理1 所构建的Stackelberg博弈中的Stackelberg均衡一定存在。

证明：根据对跟随者博弈和领导者博弈的分析，由公式(7)可知，任意无人机用户的效用函数都是关于Pi的凹函数。同理，由公式(15)可知，干扰机的效用函数是关于J的凹函数。由文献[15]可知，所构建的Stackelberg博弈至少存在一个纳什均衡解，领导者博弈与跟随者博弈的最优策略构成了Stackelberg均衡。

定理2 所构建的Stackelberg博弈中的Stackelberg均衡解是唯一的。

证明：由公式(7)和公式(15)可知，无人机用户和干扰机的效用函数是凹函数，可以将效用函数优化问题看成凸优化问题。根据凸优化理论和对偶优化理论可知，跟随者博弈与领导者博弈的最优策略是唯一的，即

(20)

证毕。

2.3 优化算法

通过上述分析，本文利用次梯度迭代算法求解Stackelberg均衡解。

次梯度迭代算法如下：

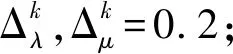
输出：Stackelberg均衡解P1,P2,…,Pn,J，即无人机用户与干扰机的最优功率。

循环：fork=0 tokmax;

1k=k+1;

2 根据无人机用户的效用函数求解功率表达式：

Pn(k+1)=Pn(J)，n=1,2,…,n；

3 根据P1(k+1)，P2(k+1)…Pn(k+1)，求解干扰机功率J(k+1);

4 更新拉格朗日乘子：

6k=kmax,结束循环。

3 仿真分析

3.1 参数设置

假设无人机用户随机分布在50 m×50 m的网格区域中，如图4所示。区域内存在7个无人机节点，其中6个无人机节点代表3个无人机用户，即每个无人机用户包含发送机与接收机。仿真参数如表1所示。

图4 无人机用户与干扰机的位置分布

表1 通信参数

3.2 收敛性分析

通过Stackelberg博弈和次梯度迭代优化算法，可以分析得到无人机用户与干扰机在同信道与部分重叠信道的Stackelberg均衡解，如图5所示(图中重叠信道指干扰机与用户2、3的信道关系)。从图中可以看到，当无人机用户与干扰机处于同信道时，双方的博弈要比部分重叠信道的博弈激烈，这是由于无人机用户与干扰机处于部分重叠信道时，会产生干扰因子，从而减弱了双方博弈的起伏程度。

图5 3用户同信道与部分重叠信道的传输功率收敛曲线

其次，在同信道与重叠信道的传输功率收敛曲线对比图中可以发现，当用户1和干扰机同时处于部分重叠信道时，干扰机的收敛功率值与同信道场景相比有所下降，3个无人机用户的收敛功率值与同信道场景相比有所提升，这说明本文提出利用部分重叠信道的特性降低干扰的想法得到验证。

同时，为了研究不同数量无人机用户的传输功率收敛情况，本文设计了部分重叠信道用户2、用户3的场景。如图6所示，通过对比部分重叠信道用户2与用户3的传输功率收敛曲线图可以发现，部分重叠信道用户3达到传输功率收敛需要更多次数的迭代，并且干扰机与无人机用户的双方博弈更加激烈。因此，可以得出结论：在多无人机通信网络中，随着无人机用户数量的增加，干扰机与无人机用户的博弈愈加激烈，需要更多的迭代次数才能达到收敛。

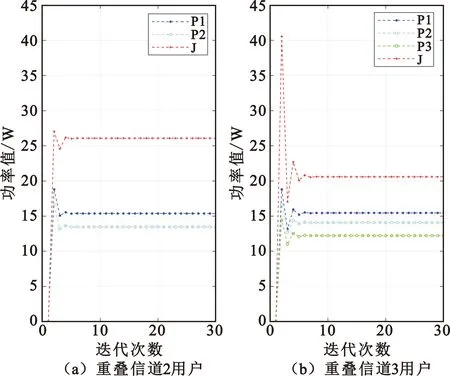
图6 部分重叠信道用户2与用户3传输功率收敛曲线图

此外，从图6中还可以发现，在部分重叠信道用户2的场景中增加1个无人机用户后，干扰机的收敛功率值会相对降低，无人机用户的收敛功率值会相对增加。因此，可以得出在多无人机通信网络中，随着无人机用户数量的增加，多无人机通信网络的抗干扰能力越强。

为了研究用户的信道增益对干扰机和用户的收敛功率值的影响，本文选择部分重叠信道用户3的场景，尝试改变用户1的信道增益α1，仿真结果如图7所示。从图中可以看到，随着用户1的信道增益α1的增加，用户1的收敛功率值逐渐增加，干扰机的收敛功率值逐渐降低，其余用户的收敛功率值相对降低。因此，可以得出用户1与干扰机之间存在竞争关系，用户1与其余用户之间也并非是合作关系，甚至存在竞争关系。

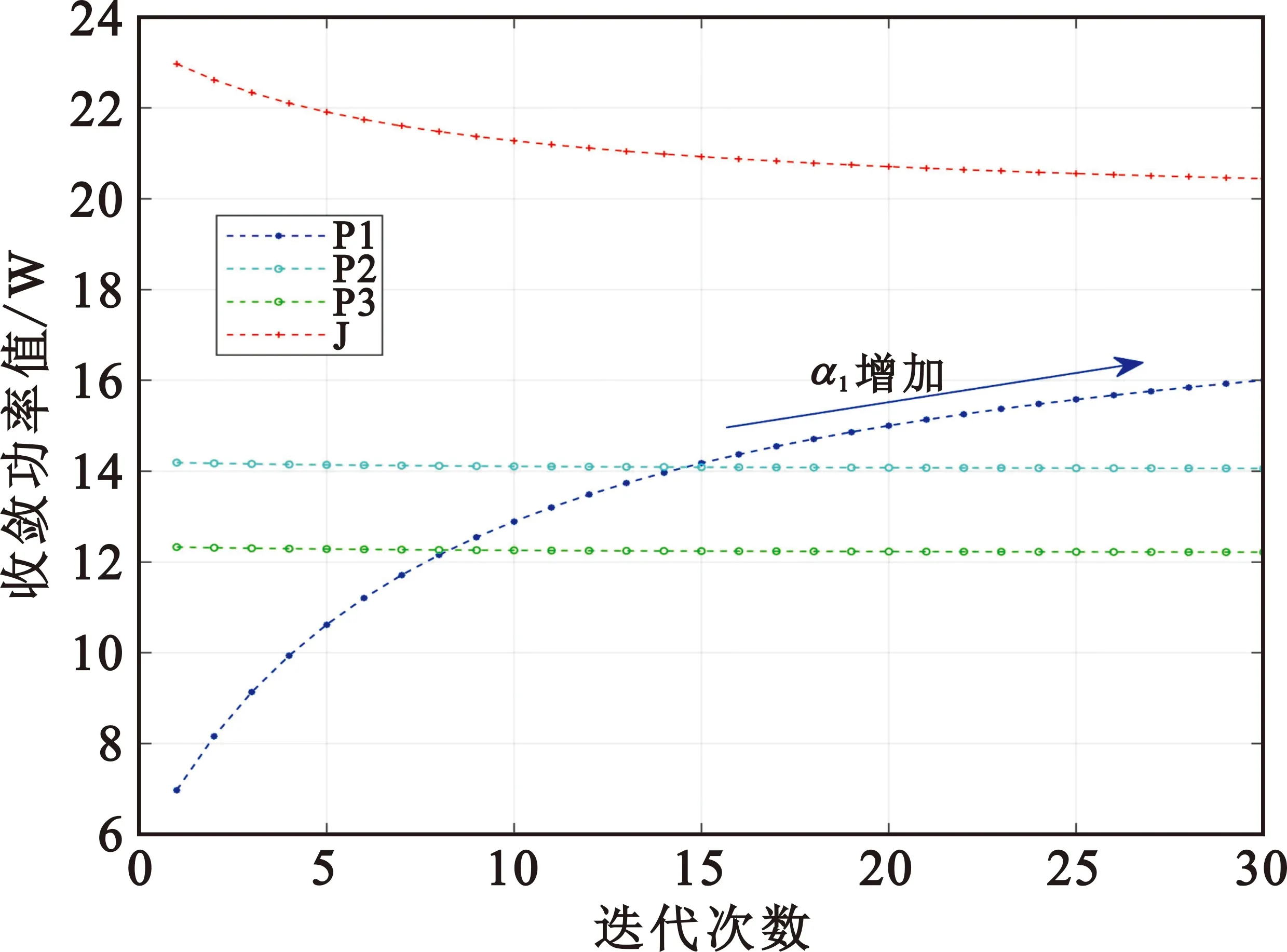
图7 信道增益α1的变化对干扰机和用户收敛功率值的影响

同理，为了研究干扰机的干扰增益对干扰机和用户的收敛功率值的影响，尝试改变干扰机的干扰增益β，仿真结果如图8所示。从图中可以看到，随着干扰机的干扰增益β的增加，用户1、2、3的收敛功率值逐渐减少，干扰机的收敛功率值逐渐增加。因此，可以得出结论：干扰机与用户群之间存在竞争关系。

图8 干扰增益β的变化对干扰机和用户收敛功率值的影响

3.3 系统效用分析

3.2节分析了用户、干扰机在同信道与部分重叠信道的功率收敛性，本节将分析用户与干扰机在同信道与部分重叠信道的效用值变化，如图9与图10所示。从图中可以看到，与同信道场景相比，部分重叠信道场景下用户的效用值相对增加，干扰机的效用值相对减少。因此，可以得出结论：利用部分重叠信道能够提高无人机用户的效用值，优化多无人机通信网络性能。

图9 无人机用户在同信道与部分重叠信道的效用值

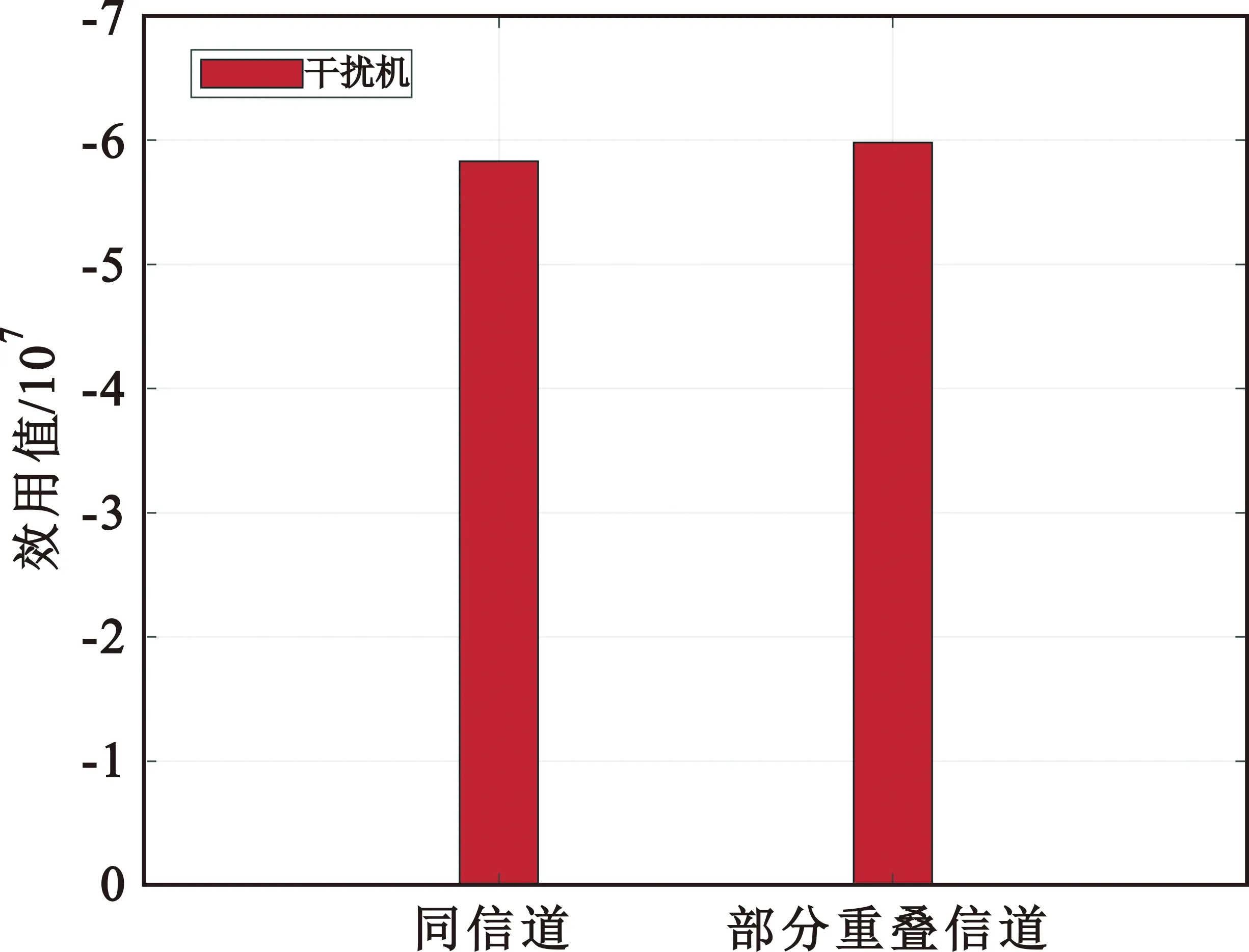
图10 干扰机在同信道与部分重叠信道的效用值

为了进一步研究干扰机对无人机用户的干扰影响，本文研究了部分重叠信道场景下干扰距离l的影响。干扰增益与干扰距离l的关系β=l-ρ， 其中ρ为路径衰落因子。图11给出了干扰距离l对用户和干扰机效用值的影响。

图11 干扰机到无人机用户的距离l对效用值的影响

从图11可以看到，随着干扰距离l增加，用户的效用值逐渐增加，干扰机的效用值逐渐降低，并且用户与干扰机的效用值增速会减缓。因此，可以得出结论：随着干扰机对用户干扰距离l的增加，干扰机对用户的干扰效果减弱。

4 结束语

本文利用部分重叠信道的特性，考虑多无人机通信网络中的外部恶意干扰与网络内部互扰，通过构建Stackelberg博弈抗干扰模型，设计无人机和干扰机的效用函数，对Stackelberg均衡解的存在性和唯一性进行了分析。在此基础上提出基于次梯度迭代的算法求解Stackelberg均衡解，并分析其收敛性能。仿真结果表明，利用部分重叠信道降低了干扰机对用户的恶意干扰、用户对用户的同频干扰，优化多无人机通信网络性能。此外，在仿真结果部分，分析了信道增益和干扰增益等参数对博弈双方收敛功率值的影响。

本文研究了多无人机通信网络抗干扰中的传输功率和信道联合优化问题，仍有许多挑战和问题值得分析和研究：一是实际应用中地形、随机干扰等不确定因素影响信道状态，从而降低多无人机通信网络性能，需要考虑更多的影响因素；二是现阶段博弈论和强化学习等理论被广泛应用在通信抗干扰领域，但学习能力强大的深度学习还未广泛应用在抗干扰领域，未来应对更加智能的干扰源，深度学习可以学习不同的干扰规律，主动规避干扰；三是现阶段无人机通信抗干扰处于理论分析阶段，实物验证尚少[16]，未来考虑将博弈论、强化学习和深度学习算法应用在无人机通信抗干扰，并通过软件无线电外设(Universal Software Radio Peripheral，USRP)实物验证算法性能。