支持一般电路的高效安全基于属性签名

黄振杰 林志伟,2

1（福建省粒计算及其应用重点实验室（闽南师范大学）福建漳州 363000）

2（交通运输部东海航海保障中心厦门通信中心 福建厦门 361026）

基于属 性签名（attribute-based signature，ABS）[1]是一种特殊数字签名体制，可以为用户提供细粒度的隐私保护，在多个领域有重要应用，因此成为密码学的研究热点.

ABS 的隐私保护控制是通过属性和属性集上定义的访问结构实现的.根据访问结构使用位置的不同，基于属性签名分为密钥策略ABS（key-policy attributebased signature，KP-ABS）和签名策略ABS（signaturepolicy attribute-based signature，SP-ABS）.在KP-ABS 中，用户从属性机构（attribute authority，AA）处获得其所拥有的访问结构所对应的签名密钥，之后可用其对属性满足其访问结构的消息进行签名.签名可以确保消息是由拥有能被指定属性满足的访问结构的用户签发的（不可伪造性），但不能辨认出签名人所拥有的具体访问结构，更不能辨认出签名人的身份（隐私性）.SP-ABS 则相反，用户从属性机构处获得其所拥有的属性所对应的签名密钥，然后对具有其属性所满足的访问结构的消息进行签名.

举个简单的说明性例子：ABS 可为教学管理系统提供匿名评价功能.假设每个课程都表示为“课程名称、开课教师姓名、开课年份、开课学期”，那么每位学生所选的课程组可以表示成(C1∧T1∧Y1∧S1)∨(C2∧T2∧Y2∧S2)∨···∨(Ck∧Tk∧Yk∧Sk)，其 中Ci,Ti,Yi,Si分别表示课程名称、开课教师姓名、开课年份和开课学期.在学生选定其课程组后，系统根据其所选课程组所对应的访问结构为其发放签名密钥，此后，学生可以使用其签名密钥匿名发表课程评价.ABS 的不可伪造性保证只有选修的学生才能对课程进行评价，其隐私性保证任何人都不能辨认出评价出自哪位学生.不可伪造性保证评价来源的合法性，隐私性保障评价者的隐私权.

由于其良好的性质，ABS 在许多领域有重要的应用，如匿名凭证（anonymous credentials）、消息传递（message delivery）、匿名认 证（anonymous authentication）、秘密泄露（leaking secrets）、信任协商（trust negotiations）、隐私接入控制（private access control）等等[1-2].

自ABS 被提出以来，众多学者先后提出许多支持各种不同访问结构的方案.Shahandashti 等人[2]、Li等人[3]、Herranz 等人[4]和Gagne 等人[5]各自提出支持门限（threshold）访问结构的ABS 方案；Maji 等人[1]和Gu 等人[6-7]各自提出支持单调（monotone）访问结构的ABS 方案；Okamoto 等人[8-9]提出支持非单调（nonmonotone）访问结构的ABS 方案；Tang 等人[10]和Sakai 等人[11]各自提 出电路（circuits）访问结构的ABS 方案；Kaafarani 等人[12]提出无界电路（unbounded circuits）访问结构的ABS 方案；Zhang 等人[13]提出支持内积（inner-product）访问结构的ABS 方案；Datta 等人[14]提出无界算术分支程序（unbounded arithmetic branching programs）访问结构的ABS 方案.

为了克服ABS 单个属性机构带来的瓶颈和信任过度集中的问题，Maji 等人[1]和Okamoto 等人[15]分别提出多属性机构（multi-authority）ABS 和去中心（decentralized）ABS.为了克服ABS 计算开销过大，不适用于资源受限场景的缺点，学者们将外包技术引入到ABS 中来，Chen 等人[16]提出外包（outsourced）ABS，Mo 等人[17]和Sun 等人[18]分别提出新的外包ABS 方案.Huang 等人[19]指出已有外包ABS 方案的隐私性缺陷，进而提出具有完善隐私性的外包ABS方案.Ren 等人[20]进一步提出可验证（verifiable）外包ABS；Cui 等人[21]和Xiong 等人[22]研究了服务器辅助（server-aided）ABS；Wang 等人[23]提出服务器辅助验证（server-aided verification）ABS.

此外，学者们还研究了具有附加性质的ABS，如基于属性环签名（attribute-based ring signature）[24]、基于属性代理签名（attribute-based proxy signature）[25]、基于属性签密（attribute-based signcryption）[26]、基于属性净化签名（attribute-based sanitizable signature）[27]等.

ABS 研究的主要目标是更高的安全性、更高的效率和更强的访问结构表达力.电路是最富表达力的访问结构之一.目前已知有3 个ABS 方案支持电路访问结构：Tang 等人[10]的方案、Sakai 等人[11]的方案和Kaafarani 等人[12]的方案.文献[11−12]方案的效率都很低，签名的长度都与电路的输入成线性关系.Tang等人[10]的方案的签名仅为1 个群元素，效率最高，但在安全性和访问结构表达力方面却比较弱：

1）Tang 等人[10]方案的不可伪造性是很弱的，只是在选定消息和选定属性攻击下存在不可伪造，只能防止敌手伪造特定消息的签名.

2）Tang 等人[10]的方案仅支持特殊电路，要求兄弟节点的深度必须相同，且都是其父节点的深度加1；要求所有输入节点的深度相同.

本文改进了Tang 等人[10]的方案，提高了安全性、丰富了访问结构表达力、缩短了数据长度并降低了计算开销.本文的主要贡献包括3 个方面:

1）增强方案的安全性.从“选定消息和选定属性攻击下存在不可伪造（existentially unforgeable under selective message attack and selective attribute,EUF-sAsMA）”提升到“自适应选择消息但选定属性攻击下存在不 可伪造（existentially unforgeable under adaptive chosen message but selective attribute attack,EUF-sACMA）”.EUF-sA-CMA 比EUF-sA-sMA 强很多，能防止敌手伪造任何自适应选择消息的签名.

2）丰富了访问结构表达力，将访问结构从特殊电路拓展到一般电路.去掉原有的所有限制，允许兄弟节点的深度不同；允许孩子节点的深度比其父节点的深度大于1，即可以跳层；允许输入节点的深度不同.另外，任意电路都可以通过德·摩根（De Morgan）定律转换成非叶子节点为“或门”或“与门”，“非门”只出现在叶子节点的电路.如果将带“非门”的叶子节点定义为1 个新属性（比如“不是教授”）作为1 个新的输入，就可以支持非单调电路.一般电路的极强表达能力使得方案可支持任意访问结构，达到任意的访问控制粒度.

3）缩短了数据长度并降低了计算开销.在保持签名大小仅为1 个群元素的前提下，将主公钥、主私钥和签名钥的大小都显著缩短；将签名密钥生成、签名生成和签名验证的计算开销都显著降低.

1 预备知识

1.1 符号说明

本文使用的符号和参数的含义如表1 所示.

1.2 多线性映射与困难性假设

多线性映射.G(1λ,k)为群生成算法，输入安全参数 λ和多线性映射级数k，输出素数p阶群序列G1,G2,···,Gk和相应的生成元g1,g2,···,gk，以及双线性映射序列ei,j：Gi×Gj→Gi+j，1 ≤i≤k−1,1 ≤j≤k−1,i+j≤k，满足

多线性映射定义为e(a1,a2,…,an)=e(a1,e(a2,…,e(an−1,an)…))，其中右侧的e为其输入所对应的双线性映射ei,j.

Table 1 Symbols Interpretation表1 符号释义

k-MCDH 假设.任意概率多项式时间算法 A 成功解k-MCDH 问题的概率都是可忽略的.

1.3 电 路

假设电路有n个输入节点，q个门节点，记输入节点集合为I={1,2,···,n}，门节点 集合为G={wn+1,wn+2,…,wn+q}，所有节 点集合 为N=I∪G，其 中wtop=wn+q为头部节点.门节点w的左、右孩子节点分别记为L(w)和R(w).GT(w)表示门节点w的类型，即“AND”或“OR”.电路记为f=(n,q,L,R,GT).

D(w)表示节点w的深度.头部节点的深度为0，其他节点的深度为其到头部节点的最长路的长度.f(Ω)表示输入为Ω ∈{0,1}n时，电路f的输出.当f(Ω)=1时，称 Ω满足f；否则，称 Ω不满足f.类似地，fw(Ω)表示输入为 Ω时，电路f中门节点w的输出.

为了有效降低计算开销，本文为电路引入节点权重的概念，用Ww(Ω)表示在输入为 Ω时节点w的权重，其计算方法如1）～3）：

1）输入节点.

①输入为1 的节点，Ww(Ω)=n−1；

② 输入为0 的节点，Ww(Ω)=∞.

2）或门.

①如果fw(Ω)=0，则Ww(Ω)=∞；

② 否则Ww(Ω)=min{WL(w)(Ω),WR(w)(Ω)}+2.

3）与门.

①如果fw(Ω)=0，则Ww(Ω)=∞；

② 否则：

如果D(L(w))=D(R(w))，则

如果D(L(w))≠D(R(w))，则

这样定义的节点权重其实就是使用本文方案生成签名时，使用该节点所需要计算的对运算的数量.对运算越少，效率就越高.

图1 给出一个一般电路的说明性例子：

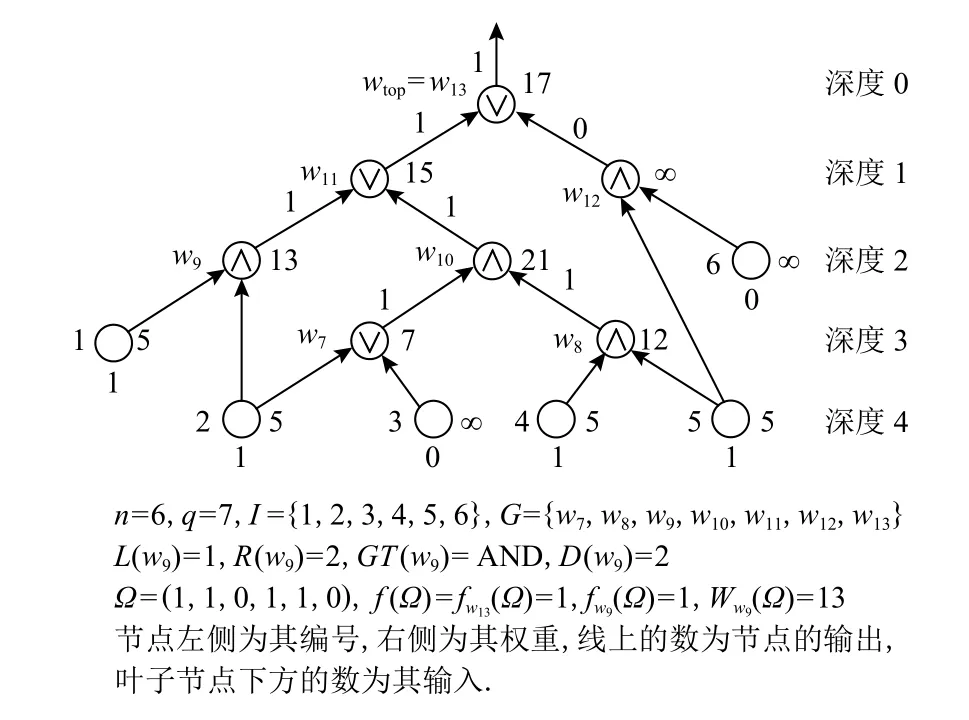
Fig.1 Example of general circuit图1 一般电路示例

2 电路访问结构密钥策略ABS

本节给出访问结构为电路的密钥策略ABS 的定义和安全模型.

2.1 算法组成

电路访问结构密钥策略ABS 方案由1）～4）算法组成：

1）Setup(1λ,n,ℓ).输入安全参数 λ、电路输入数n和最大深度ℓ，输出系统公开参数pp和系统主私钥msk.

2）KeyGen(pp,msk,f).输入系统公开参数pp、系统主私钥msk和电路f，输出电路f所对应的签名密钥S Kf.

3）Sign(pp,S Kf,M,Ω).输入公开参数pp、签名密钥S Kf、消息M及其属性 Ω，输出关于(M,Ω)的签名 σ.

4）Verify(pp,M,Ω,σ).输入公开参数pp、消息M、属性 Ω和签名 σ.如果 σ是关于(M,Ω)的有效签名，输出1；否则，输出0.

2.2 安全性模型

定义1.正确性.一个电路访问结构的密钥策略ABS 方案是正确的，如果对于任意的消息M和满足f(Ω)=1的任意属性 Ω与电路f都有概率，则

不可伪造性.大多数ABS 的文献使用如下不可伪造性定义，其形式化模型如Game1：

Ga me1（EUF-sA-CMA）.

1）Initialization.敌手 F选择挑战属性 Ω∗并发送给挑战者 C.

2）Setup.挑战者 C生成系统公开参数pp并发送给敌手 F.

3）KeyGen Oracle.敌 手 F提交电 路f给挑战 者C .C返回电路f的密钥S Kf给 F.

4）Sign Oracle.敌手 F提交消息M和属性 Ω给挑战者 C .C返回(M,Ω)的签名 σ 给 F.

5）Forgery.敌手 F输出(σ*,M*,Ω∗).

如果下面①～③都满足，称敌手赢得Game1.

①σ*是关于消息M*和属性 Ω*的有效签名；

② (M*,Ω*)没有被询问过Sign Oracle；

③任何询问过KeyGen Oracle 的电路f都 使f(Ω∗)=0.F

定义2.一个电路访问结构密钥策略ABS 方案称为自适应选择消息但选定属性攻击下存在不可伪造的；如果对于任何多项式时间敌手 F，其赢得Game 1的优势是可忽略的.

Tang 等人[10]方案的不可伪造性是很弱的“选定消息和选定属性攻击下存在不可伪造”，其Game 和Game1 基本相同，只是Initialization 应改为：

Initialization.敌手 F选择并发送挑战消息M∗和挑战属性 Ω∗给挑战者 C.

完善隐私性.本文方案和Tang 等人[10]方案都实现了完善隐私性，任何敌手即使拥有无限的计算能力也无法识别用于生成签名的电路.

定义3.如果对于任何M，Ω和满足f0(Ω)=f1(Ω)=1的f0,f1，使用f0和f1所产生的签名分布

是信息论意义不可区分的，则称该电路访问结构密钥策略ABS 方案具有完善隐私性.

3 一般电路密钥策略ABS 方案

本节提出一个支持一般电路的密钥策略ABS 方案.

3.1 主要设计思想

本文方案是基于Tang 等人[10]方案改进而来的，改进的主要思想如1）～4）所描述：

1）以唯一的头部节点为参照原点，其他节点都参照它进行定位，以便支持一般电路.而Tang 等人[10]方案采用叶子（输入）节点为参照原点，所以需要假设所有输入节点均有相同的深度.

2）引入节点权重的概念并采用“从上到下”递归的方式计算签名，只计算必须计算的且权重较小的节点的Ew.而Tang 等人[10]方案“自下而上”计算所有输出为1 的节点的Ew，许多不必要的Ew也计算了，浪费了计算资源.

3）充分利用左右孩子节点的对称性，将孩子节点同深度的门节点的密钥都减少了1 个分量，“或门”的密钥减少了25%，“与门”的密钥减少了33.33%.孩子节点有不同深度的门节点的密钥没有减少，只是为了在安全性证明中方便仿真密钥.实际使用时同深度和不同深度的门节点可不加区别，都减少1 个分量.

4）通过使用安全Hash 函数，将不可伪造性提升到“自适应选择消息但选定属性攻击下存在不可伪造”，同时将主公钥和主私钥长度各减少2m个元素（m为消息的长度）.

3.2 签名方案

本文所提出的一般电路密钥策略ABS 方案的算法为：

Setup.输入安全参数 λ、电路最大深度 ℓ和电路输入数n.

1）运行G(1λ,k=n+ℓ+3)得到阶为素数p的群序列G1,G2,…,Gk和对应的生成元序列g1(g=g1),g2,···gk，以及其上的多线性映射e.

2）随机选取ai,β∈RZp，i∈[1,n],β∈{0,1}，计算Ai,β=.记a={a1,0,a1,1,a2,0,a2,1,…,an,0,an,1}，A={A1,0,A1,1,A2,0,A2,1,…,An,0,An,1}.

3）随机选取α∈RZP，计算Y=

4）选取防碰撞Hash 函数H:{0,1}∗→G1.

输出系统公开参数pp={Y,A,n,ℓ,p,G1,G2,…,Gk,g1,g2,…,gk,e,H}和主私钥msk={α,a}.

KeyGen.输入系统公开参数pp、系统主私钥msk和电路f=(n,q,L,R,GT).

2）采用“自下而上”的方式计算密钥组成部分Kw.

①输入节点.w∈I=[1,n] ，D(w)=iw，计算

② 或门.w∈G，GT(w)=OR ，D(w)=iw.

（i）如果D(L(w))=D(R(w)),即iL(w)=iR(w),计算

③与门.w∈G，GT(w)=AND ，D(w)=iw.

（i）如果D(L(w))=D(R(w)),即iL(w)=iR(w),计算

3）输出签名密钥S Kf={Kw}w∈N.

Sign.输入公开参数pp、签名密钥S Kf、消息M和属性Ω=(Ω1,Ω2,…,Ωn)∈{0,1}n，计算f(Ω)和各节点的权重.如果f(Ω)=0，无法签名，停止；如果f(Ω)=1，按“从上到下”递归方法计算必要节点的Ew.

2）或门.w∈G，GT(w)=OR.

如果WL(w)(Ω)≤WR(w)(Ω)，调用其左孩子节点的EL(w)，计算

否则，调用其右孩子节点的ER(w).

如果D(L(w))=D(R(w))，计算

如果D(L(w))≠D(R(w))，计算

3）与门.w∈G，GT(w)=AND，调用其孩子节点的EL(w)和ER(w).

如果D(L(w))=D(R(w))，计算

如果D(L(w))≠D(R(w))，计算

4）输入节点.w∈I.计算

5）计算并输出签名

Verify.输入待验证的签名 σ及相应的消息M和属性 Ω.如果等式

成立，输出1；否则，输出0.

4 安全性证明与性能效率分析

本节证明所提出方案的安全性，并分析其性能和效率.

4.1 安全性证明

定理1.本文所提出的一般电路密钥策略基于属性签名方案是正确的.

证明.容易知道，在签名递归过程所有被计算的节点都有fw(Ω)=1.下面，用数学归纳法证明签名生成过程中所有的Ew都有Ew=其中ϱ(Ω)=

1）当w为输入节点时，即w∈I，D(w)=iw，有

①或门.w∈G，GT(w)=OR.

② 与门.w∈G，GT(w)=AND.

定理2.如果k-MCDH 假设成立，则所提出的一般电路密钥策略ABS 方案是自适应选择消息但选定属性攻击下存在不可伪造的.

证明.假设 F是具有优势 ε的EUF-sA-CMA 敌手，C 是k-MCDH 问题的挑战者，我们构建如下的算法 B，利用 F来解k-MCDH 问题.

B 维护一个初始化为空的列表 LH.令qs为查询Sign Oracle的最大次数.

k-MCDH Gen.

3）B 发送公 开参数pp={Y,A,n,ℓ,p,G1,G2,…,Gk,g1,g2,…,gk,e}给敌手 F .

KeyGen Oracle.当敌手 F 询 问关于电路f=(n,q,L,R,GT)的密钥时，如果f(Ω∗)=1，拒绝；否则，采用“自下而上”的方式计算密钥组成部分Kw.

1）输入节点.w∈I，D(w)=iw.

2）或门.w∈G，GT(w)=OR ，D(w)=iw.

①如果fw(Ω∗)=1，选取zw,vw∈RZp.

3）与门.w∈G，GT(w)=AND ，D(w)=iw.

4）最后，返回S Kf={Kw}w∈N给敌手 F.

H-Oracle.当敌手 F询问消息Mi的Hash 值时，如果Mi在 LH中，则返回相应的hi；否则，B 响应如1)～4):

1）选取ρi∈{0,1}，使ρi=0的概率为(qs+1)−1.

2）如果ρi=1，选取ri∈RZp，令hi=gri.

3）如果ρi=0，令hi=

4）返回hi给敌手 F，添加(Mi,hi,ri,ρi) 到 LH.

Sign Oracle.当敌手 F询问关于消息Mj和属性Ωj的签名时，B先请求关于消息Mj的H-Oracle 服务，从LH中得到相应的rj和 ρj.如果ρj=0，则中止；否则，计算并返回

由于上述Setup，KeyGen，H-Oracle,Sign Oralce 的仿真都是完善的，如果 B 没有中止，F输出1 个有效签名的概率至少为ε.

因为ρi=0的概率是(qs+1)−1，B在Sign Oralce 中不中止的概率至少为因此，B解k-MCDH 问题的概率至少为

当n→∞时，概率等于因此，在k-MCDH 假设下，所提出的一般电路密钥策略基于属性签名方案是自适应选取消息但选定属性攻击下存在不可伪造的.

证毕.

定理3.所提出的一般电路密钥策略基于属性签名方案具有完善隐私性.

证明.对于任何M,Ω和满足f0(Ω)=f1(Ω)=1的f0,f1，对应于f0,f1的签名分布σ0←和σ1←分别为

分布{σ0}和{σ1}是完全一样的,因此是信息论意义不可区分的，所以所提出的方案具有完善隐私性.

证毕.

4.2 性能与效率分析

与已有方案相比，本文方案有2 个显著优点：一是访问结构的表达能力达到最强，可以支持任意访问结构；二是签名只有1 个群元素，长度达到最短.

正前文所指出的，目前只有3 个支持电路访问结构的基于属性签名方案：Tang 等人[10]方案、Sakai 等人[11]方案和Kaafarani 等人[12]方案.文献[11-12]方案的签名的长度都与电路的大小成线性增长关系，效率都很低，Tang 等人[10]方案的签名大小也仅为1 个群元素.

将本文方案与Tang 等人[10]方案进行比较，结果如表2 所示.本文方案在安全性和访问结构的表达力方面都有明显优势.

因为不同的电路会有不同的数据规模和计算开销，本文以图1 的电路和1 个输入为n=64的电路为例进行效率比较，结果如表3 所示.当n=64，属性的数量是264（>7.38×1019），电路f的数量更是不受限制，因此能完全满足应用需要.

Table 2 Performance Comparison of Schemes表2 方案性能比较

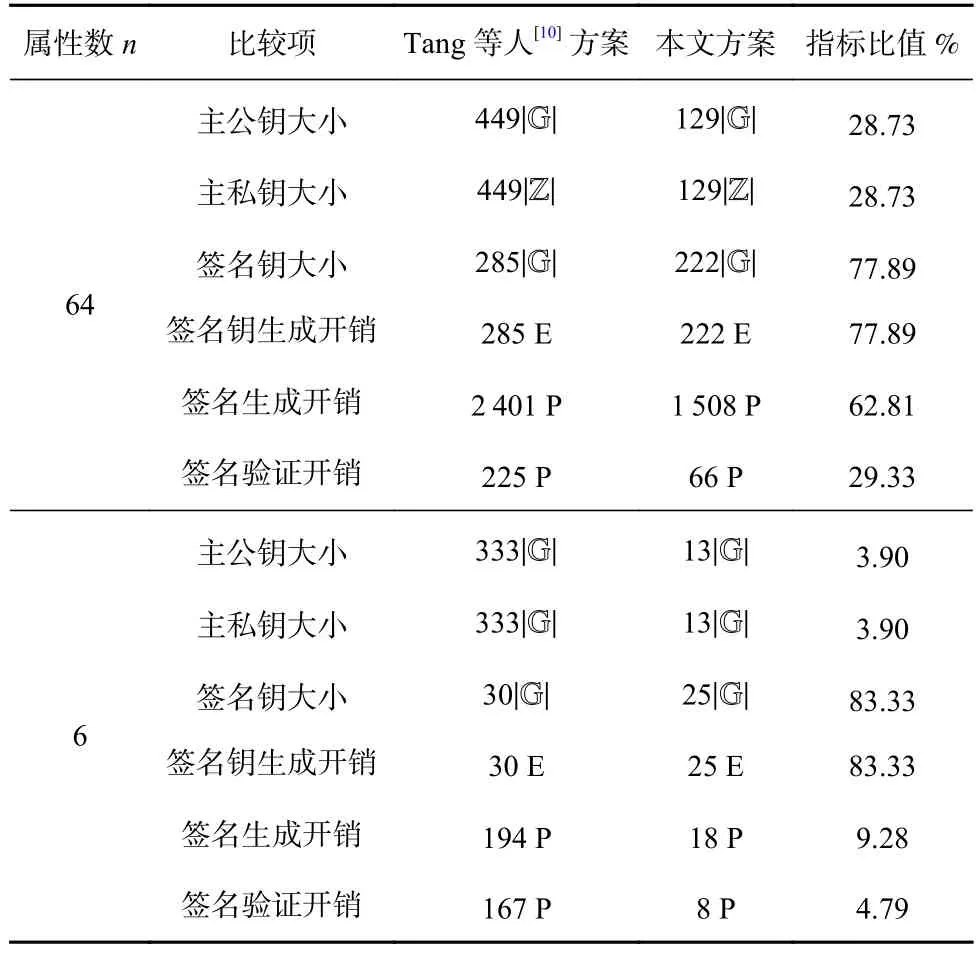
Table 3 Efficiency Comparison of Schemes with m Equals 160表3 方案效率对比（m=160）

比较结果表明：本文方案在数据长度和计算开销2 方面性能都具有优势.

5 结论

ABS 能提供灵活的隐私保护，在许多场景有重要应用.本文使用多线性映射构造了一个密钥策略的ABS 方案，可支持一般电路作为访问结构.与同类方案相比，本文方案在安全性、访问结构表达力、数据长度和计算开销等方面都有明显优势.

进一步研究的方向将是提出自适应选择消息且自适应选择属性攻击下存在不可伪造的方案，且在标准模型下证明其安全性.

作者贡献声明：黄振杰负责方案设计、安全性证明和定稿；林志伟负责方案设计、性能分析和初稿撰写.