抽象解释及其应用研究进展
2023-03-02陈立前范广生尹帮虎
陈立前 范广生,3 尹帮虎 王 戟,3
1(国防科技大学计算机学院 长沙 410073)
2(国防科技大学系统工程学院 长沙 410073)
3(高性能计算国家重点实验室(国防科技大学)长沙 410073)
抽象解释是一种对用于形式描述复杂系统行为的数学结构进行抽象和近似并推导或验证其性质的理 论,由Patrick Cousot[1-2]和Radhia Cousot[1]于20 世纪70 年代提出.抽象解释提供了一个通用的理论框架,使得人们能够在该框架下讨论不同形式化方法各自能提供的理论保证,如可靠性、完备性、不完备性等.例如,基于抽象解释,人们能够解释调试、演绎证明、模型检验、静态分析等方法的优势和局限性.
目前,抽象解释在语义模型、不变式生成、程序分析验证、混成系统验证、程序转换、系统生物学模型分析等领域取得了广泛应用.在抽象解释的发展过程中,除了理论本身的发展完善,也涌现出了一批优秀的抽象解释工具.20 世纪90 年代,研究人员开发了基于抽象解释的静态分析工具Polyspace,并成功商业化[3].2003 年左右,Blanchet 等人[4]基于抽象解释开发了静态分析工具Astrée[4],并商业化[5],它主要用于检测C 语言编写的运算密集型安全攸关嵌入式实时软件系统中运行时的错误(包括算术溢出、除零错、数组越界等),并成功对空客A340(约13.2 万行C 代码)、A380(约35 万行C 代码)等系列飞机的飞行控制软件进行了分析,实现了“零误报”,这是当时验证工具在验证规模上的重大突破.2015 年,Miné等人[6]进一步开发了面向多线程并发程序的静态分析工具AstréeA,它作为Astrée 的并发版本,已实际应用于空客飞行系统软件,所分析程序的最大规模达百万行.
近年来,抽象解释在理论与应用方面都取得了进一步发展.本文重点介绍最近5 年抽象解释在理论、基于抽象解释的程序分析、基于抽象解释的可信人工智能和其他典型应用等方面的进展,并讨论抽象解释领域未来的发展方向.
1 抽象解释理论
本节主要介绍抽象解释的基本概念、理论及抽象域方面的进展.
1.1 基本概念
抽象解释为建立具体空间与抽象空间之间的联系提供了形式化的理论方法.我们将具体空间中推理对象的集合及其上的操作所构成的数学结构称为“具体域”,而将抽象空间推理对象的集合及其上的操作所构成的数学结构称为“抽象域”.抽象解释理论利用Galois 连接来形式化地描述具体域与抽象域之间的关系.对于给定的2 个偏序集
抽象解释通过在抽象域上计算抽象函数的不动点来获得抽象语义,并基于此进行推理.抽象解释提供了严格的理论来保证基于上近似抽象的推理的可靠性,即所有基于上近似抽象推理得出的抽象空间中的性质在具体空间中也必然成立.但是,由于上近似抽象引入了精度损失,抽象解释不保证所有在具体空间中成立的性质都能基于上近似抽象推理得到.
1.2 理论进展
在理论框架方面,Cousot 等人[7]提出了一种称为A2I(abstract2interpretation),也称元抽象解释的技术,它用于对基于抽象解释的程序分析作进一步的抽象解释,即应用抽象解释对程序分析工具的性质开展分析.A2I 既可离线应用也可在线应用.离线A2I既可在分析程序之前开展(如变量打包技术),也可在分析程序之后开展(如警告诊断);在线A2I 则既可在分析程序过程中开展(如面向数值抽象域的动态变量划分技术),也可用于优化底层程序分析的精度和效率,如应用A2I,可以在原有程序分析基础上构建更加高效、更加精确的程序分析算法.换言之,A2I提供了一种通用的方法,使得不仅能应用抽象解释分析程序的性质还能应用抽象解释分析程序分析工具的性质.
Bruni 等人[8]在抽象解释框架下提出了局部完备性(local completeness)概念,它只考虑特定的而非所有的输入,并定义了一种支持局部完备抽象解释推理的逻辑LCLA,通过结合上近似和下近似,可支持某些程序规约的正确性(程序不存在错误)和不正确性表示,断言Q是post[c](P)的最强后置条件的下近似,(程序存在错误)证明.该逻辑LCLA通过 ⊢A[P]c[Q]来且使得Q在抽象域A上的抽象和post[c](P)一致.⊢A[P]c[Q] 不仅保证了Q中的所有报警都是正报,还保证了若Q中没有报警则c是正确的.因为LCLA逻辑对于非局部完备抽象域不适用,需要修复这些抽象域以满足局部完备性.为此,Bruni 等人[9]进一步提出了一种称为抽象解释修复(abstract interpretation repair)的方法,展示了如何利用局部完备性的概念以一种最优的方式来精化抽象域,以增强程序验证的精度.应用这种方法,并不要求在分析之前选择合适的抽象域,而是可以从任意抽象域开始,对其需达到的局部完备性逐步进行修复.抽象解释修复技术之于抽象解释,类似于反例制导抽象精化技术之于抽象模型检验.该工作给出了最优局部完备精化存在的充要条件.基于此,提出了2 种修复策略,使得能够在一个给定的抽象计算上消除所有的误报:一种策略是随着具体计算进行前向修复;另一种是在抽象计算过程中进行后向修复.换而言之,抽象解释修复的目标是找到最为抽象的,但又能消除不完备抽象计算中所有误报的抽象域.不过,到目前为止,如何找到充分条件保证抽象解释修复的终止性依然是开放的研究问题.最近,Campion 等人[10]提出了一种理论来对抽象解释中分析的不精确性带来的误差的传播进行估计.其主要思想是在抽象域上增加了一个度量距离的操作,用于度量不同抽象域元素之间的相对不精确程度.该工作引入了部分完备性(partial completeness)的概念.部分完备性允许产生一些误报,但是误报数量是有界的.部分完备性使得能够通过调整在分析中允许的噪声的量,来对不完备分析进行精化.该工作设计了一个证明系统来估计抽象解释器在程序分析过程中累积误差的上界.在该证明系统中,用 ⊢A[Pre]P[Post,ε]来表示后置条件Post在抽象域A上的抽象和程序P在输入Pre上具体语义下结果的抽象之间的距离不超过ε.ε可理解为抽象解释器在分析输入满足Pre的程序P的过程中累积的不精确度的上界.ε部分完备性表示抽象解释的不精确的程度不超过ε,即,具体语义下结果的抽象和抽象解释在给定输入下的分析结果之间的距离不超过ε.
另外,在抽象解释的完备性相关研究方面,Bonchi 等人[11]展示了共归纳up-to 技术(最初用于并发系统互模拟证明)与抽象解释存在关联关系.具体而言,在一定假设下,共归纳可靠up-to 技术与完备抽象技术之间存在理论上的联系,这样2 种技术之间可以进行技术迁移.Bruni 等人[12]将程序的外延(功能)等价性一般化为抽象等价性.2 个程序是外延等价的,当且仅当2 者在具体语义下是等价的.2 个外延等价的程序,可能具有不同的抽象语义(如,因为程序代码进行了变换,导致抽象语义产生了差异).文献[12]工作引入了完备团(completeness cliques)和不完备团(incompleteness cliques)的概念来对程序进行分类.完备团C(P,A)表示所有与程序P语义等价,且抽象域A对其而言是完备的那些程序构成的集合;不完备团(P,A)表示所有与程序P语义等价、且抽象域A对其而言不是完备的那些程序构成的集合.换言之,C(P,A)表示所有应用抽象域A分析得到的结果是足够精确(无误报)的程序P的变种构成的集合;而(P,A)表示所有应用抽象域A分析得到的结果是不够精确的(存在误报)的程序P的变种构成的集合.应用抽象等价性的概念,可以帮助理解代码迷惑技术和程序分析精度之间的关联关系.
在抽象解释效率优化方面,Stein 等人[13]提出了一种结合了增量式和按需驱动的抽象解释技术,其核心是定义了一种动态演进的按需抽象解释图表示,它能够显式地表示程序语句、抽象状态和分析过程中计算之间的依赖关系.基于这种图表示,程序编辑、用户产生的查询、抽象语义计值能够统一处理,不同于已有的增量式或按需驱动的技术,该技术适用于任意抽象域(包括带加宽操作的抽象域).Wei 等人[14]提出了分阶段抽象解释器(staged abstract interpreter)的概念.在编译技术中,分阶段解释器是一个编译器,它针对一个给定程序,将解释器定制化得到一个等价的但是运行效率更高的可执行程序.抽象解释器是一个程序分析器,如果将定制化技术应用于抽象解释器将得到一个分阶段抽象解释器.文献[14]的工作将部分求值技术中的第一Futamura 投影定理[15]从应用于具体解释器扩展到应用于抽象解释器,从而能够得到一个分阶段抽象解释器.分阶段抽象解释器可用于对静态分析进行优化,且使得实现优化仅需要较小的工程量且又不损害可靠性.
抽象解释为设计不变式推导方法提供了一个通用框架,而性质制导可达性(property-directed reachability,PDR),也称IC3,则是近年来不变式推导领域的重要突破之一.最近,Feldman 等人[16]展示了PDR 与抽象解释之间在理论上的关联关系,即命题PDR 可以转换为逻辑抽象域上的一个抽象解释算法.具体而言,该工作设计了PDR 的一个变种版本,称为∧-PDR,其中反例的所有一般化都被用来增强(用于构造归纳不变式的)公式序列,以阻止反例.该工作展示了∧-PDR 推导不变式过程对应于抽象域上最佳转换子上的Kleene 迭代.
1.3 抽象域进展
抽象域是抽象解释框架的核心要素,也是抽象解释在实践中取得成功应用的一个关键因素.抽象域包括抽象语义的选择、数据结构和算法的设计、实现的决策等方面.抽象解释框架提供了构造性的和系统性的方法来设计、组合、比较、研究、证明和应用抽象域.到目前为止,已经涌现出数十种抽象域.大致可以分为2 类:数值抽象域(区间、同余、八边形、多面体、多项式等)和符号抽象域(如形态、树).抽象解释为抽象域提供了各种通用的算子(乘积、幂集、补全等).抽象域已经广泛应用于各种系统(硬件、软件、神经网络等)的多种性质(安全性、终止性、概率性质等)的分析验证中.目前,也出现了多个开源抽象域库,如APRON[17],ELINA[18],PPL[19],PPLite[20],VPL[21]等.
近年来,在提升抽象域的计算效率方面,Singh等人[22-23]提出了一种降低数值抽象域时空开销但又不影响分析精度的分解(decomposition)技术.其主要思想是:根据变量之间以及变量与程序语句之间的依赖关系,将一个抽象域元素分解为程序变量集的不相交子集上抽象域元素的笛卡尔乘积.这样,抽象域算子不需要应用于整个抽象域元素上,而只需要应用于其中相关的部分上,从而减少时空开销.这种技术适用于任意基于线性约束表示的数值抽象域,如八边形、多面体.从实现角度,对变量集应用分解技术之后,可以通过手工方式实现域操作的分解(即需要人工重新实现抽象域的域操作),以使得域操作能适用于变量集的划分.进一步,Singh 等人[18]提出了一种通用的在线分解技术,在分析过程中自动动态调整变量集划分,能够在不改变原抽象域操作的基础上自动实现基于在线分解的抽象域优化.实验结果表明,在不损失分析精度的前提下,分解技术能获得极大的性能提升.比如,基于分解技术优化后的八边形抽象分析的性能提升超过百倍[22].Singh等人基于分解技术实现了开源的抽象域库ELINA[18].最近,Gange 等人[24]基于加权有向图的切分规范型(split normal form),给出了Zone 抽象域和八边形抽象域的高效实现方法.图表示上的闭包算法是这2 个抽象域的核心算法.这2 个抽象域的传统实现方法在图表示上基于Dijkstra 最短路径闭包算法计算闭包时,会根据变量界{x≥c1,y≤c2}引入差分界约束y−x≤c2−c1,使得x和y建立了关联关系,从而使得图表示更稠密,进而影响了效率.引入切分规范型的主要目的是尽量保持内部图表示的稀疏性,同时使得闭包更高效.比如,重新计算图的闭包时,避免加入因变量界信息引入的约束关系.此外,考虑抽象域操作对抽象状态的增量式更新,Chawdhary 等人[25]最近针对八边形抽象域设计了平方复杂度的增量式算法来计算闭包,提升了八边形抽象域的计算效率.
在提升抽象域表达能力方面,Chen 等人[26]基于二叉决策树设计了一个抽象域函子,其中树的分支节点为路径布尔条件,叶节点为数值或符号抽象域,以提升抽象域在依赖路径的静态分析中的精度.最近,Chen 等人[1,27-28]在抽象域域表示中加入了对程序变量的值与绝对值间关系的刻画,设计实现了线性绝对值等式抽象域,能够推断程序中一部分分段线性行为(如条件分支、绝对值函数调用和最大或最小值函数调用等)所蕴含的非凸析取性质.在析取区间分析方面,Gange 等人[29]使用范围决策图(range decision diagrams)代替二叉决策图,重新设计实现了Gurfinkel 等人[30]提出的Boxes 抽象域(该抽象域能够表达多个Box 的析取并刻画部分路径条件信息),使得Boxes 抽象域的实现更高效、对于非线性表达式的精度也更高.
在多面体抽象域实现方面,Maréchal 等 人[31]提出了基于参数线性规划的最小化算子(用于消除域表示中的冗余约束),使得仅基于约束表示的多面体抽象域库VPL 相比原来提升了几个数量级的性能,并与已有基于传统双重描述法的多面体抽象域实现性能相当.Becchi 等人[32]针对支持严格不等式约束的未必封闭多面体域[33],提出了一种多面体域双重描述法的新表示方法及其相应的类Chernikova 转换算法,这种表示方法完全没有使用松弛变量,极大提升了分析效率.进一步,Becchi 等人基于该工作开发了相应的开源抽象域库PPLite[19].
2 基于抽象解释的程序分析
抽象解释理论为静态程序分析的设计和构建提供了一个通用的框架,并从理论上保证了所构建的程序分析的终止性和可靠性.程序分析是抽象解释最主要的应用之一.本节主要介绍抽象解释在程序分析中的应用及其进展.
2.1 技术进展
本节介绍基于抽象解释的程序分析的最新技术进展,主要包括如何提高分析的精度、可扩展性和可用性等3 个方面.
1)提高精度
抽象解释通过迭代计算求解程序语义方程系统的解,即抽象不动点,从而得到程序不变式.当前学术界和工业界的抽象解释工具基本都采用传统的不动点迭代算法,即包含加宽和变窄算子的混沌迭代(chaotic iteration)算法.最近,Amato 等人[34]提出在分析过程中交织使用加宽和变窄算子的迭代策略,打破混沌迭代算法中先应用加宽算子再应用变窄算子的固定顺序,使得不动点迭代计算结果更加精确.Boutonnet 等人[35]提出利用初次迭代计算得到的基本解与加宽点处后向收集的信息来确定一个启动点,然后重复应用加宽和变窄操作以得到更精确的结果.
抽象解释通过加宽算子来加快收敛速度并保证终止性,从而实现高效分析.然而,加宽操作引入的精度损失极大影响了迭代计算的精度.为此,已有工作[4,34]提出了多种方法来减少加宽带来的精度损失.设置加宽阈值是弥补加宽精度损失的常用技术.不同于固定的加宽阈值设定,Cha 等人[36]基于对加宽精度有影响的程序特征,利用机器学习的方法对大量代码的分析结果进行学习,从而得到适应不同程序的加宽阈值的最优设定策略.
抽象域作为抽象解释的重要组成部分,其表达能力直接决定了抽象解释分析能力.现有抽象域大多数为线性的数值抽象域,且不能表达非凸性质.为弥补抽象域自身表达的局限性,除了设计新的能够刻画析取、非线性的抽象域,将现有抽象域与其他方法结合是另一种解决方案,这方面近期研究主要可分为2 类:
①通过符号化抽象[37](symbolic abstraction)求解抽象域的最佳抽象迁移.随着近年来最优化模理论(optimization modulo theories,OMT)的发展[38-39],符号化抽象得到进一步发展.Jiang 等人[40]提出了结合抽象域与可满足性模理论(satisfiability modulo theories,SMT)块级抽象解释技术,其主要思想是:把整个程序划分为一个个程序块;程序块的迁移语义采用SMT 公式来精确编码,块间信息的传递使用抽象域表示;在出程序块时,应用OMT 技术把SMT 公式抽象为抽象域表示;在循环头,采用抽象域上的加宽操作,来保证分析的终止性.这种技术实现了抽象域与SMT 的优势互补,提升了抽象解释分析的精度.Yao等人[41]提出了针对无量词位向量公式的符号化抽象算法,并将其应用于符号化区间抽象和符号化多面体抽象.该工作在设计符号化抽象时,主要基于2 项观察:程序变量之间往往具有关联关系;区间抽象域和多面体抽象域在位向量算术下是有界的.该工作利用这2 项观察来减少冗余计算和缩减符号化抽象的搜索空间,从而提升了基于OMT 的符号化抽象的效率.
②提高抽象域的非线性表达能力.基于组合递推分析(compositional recurrence analysis)[42]将符号化分析与抽象解释结合起来可以生成多项式、指数、对数等形式的非线性不变式,并且能取得与抽象精化同样精确的结果.Kincaid 等人[43]最近还将组合递推分析进一步应用于递归程序分析与资源界分析中,并在结合多种数值推导方法后提升了多种非线性数值不变式生成的精度与效率[44].此外,Allamigeon 等人[45]提出基于椭圆幂集的方法来生成析取二次不变式.
通过抽象解释与动态分析的结合,同样可以提升程序分析的精度.针对目前基于抽象解释的程序验证技术存在的不变式精度不够、没有利用目标性质以及不擅长产生反例等问题,Yin 等人[46]提出了一种待验证性质制导的、结合迭代抽象解释和有界枚举测试的程序验证框架,通过前/后向抽象解释分析的迭代精化以及与测试技术的结合,提升基于抽象解释的程序验证的能力.Toman 等人[47]最近提出了结合具体测试和抽象解释技术的框架Concerto,用以分析基于框架的应用程序,其中,利用具体测试来分析框架实现部分,使用抽象解释来分析应用代码部分.Chen 等人[48]提出了一种贝叶斯框架DynaBoost,使用从动态测试执行过程中获得的信息来对基于抽象解释的静态分析的报警进行优先级排序,以减少静态分析的误报.
最近,O'Hearn[49]提出了不正确性逻辑(incorrectness logic),作为霍尔逻辑(用于证明程序不存在错误)对偶的版本,用于证明程序存在错误.不正确性逻辑三元组 [presumption]f[ϵ:result] 表示,任何满足结果 条件result的最终状态可由满足前提条件presumption的初始状态执行f后得到,其中,ϵ为ok(表示正常结束)或er(表示错误结束).基于不正确性逻辑,目前衍生了不正确性分离逻辑[50]和不正确性并发分离逻辑[51],在此基础上设计实现的工具Pulse-X[52]已经可以实现对OpenSSL 内存漏洞的检测.不正确性逻辑采用下近似推理.在文献[49]中,O'Hearn 讨论了如何使用抽象解释理论指导和解释不正确性逻辑问题,即如何利用基于抽象解释的程序分析查找真实的错误.沿着这一思路,Ascari 等人[53]讨论了设计下近似抽象域所面临的困难.
2)提高可扩展性
提升抽象解释可扩展性,使其支持更大规模程序的高效分析,是抽象解释在实际中成功应用的关键.近期相关研究进展主要包括3 个方面.
①改进抽象解释框架下不动点迭代算法.基于程序依赖图弱拓扑序(weak topological order)的混沌迭代过程为串行执行,具有三次方的最坏时间复杂度,并且可能会因为过深层次的程序依赖而导致栈溢出.为此,研究人员考虑通过不动点迭代的并行执行来提升分析的可扩展性.最近,Kim 等人[54]在抽象解释工具IKOS[55]中将混沌迭代的弱拓扑序扩展为弱偏序(weak partial order),并基于计算循环嵌套森林的算法[56],提出了一种最坏线性时间复杂度的确定性并行不动点迭代算法,并在16 核上开展了实验,在保证与串行分析结果一致的同时,性能最大提升10.97倍.不同于利用CPU 并行处理能力,内存优化同样可以提升不动点迭代性能.Kim 等人[57]提出了一种近似线性时间复杂度的不动点迭代算法,通过在混沌迭代过程中及时释放存储抽象值的内存,并在不动点计算期间而非计算结束后执行断言检查,使得IKOS 在缓冲区溢出过程间分析时的内存使用峰值平均降低到43.7%.
②基于抽象解释的参数化程序分析[58].参数化程序分析将程序分析视为黑盒,寻找程序分析在性能表现、精确性和可靠性间的权衡.在这方面研究中,机器学习的方法发挥了重要作用.Heo 等人[59]利用支持向量机学习在哪些可能的程序构件中允许采用非可靠的分析方法,并保留正确报警,以提升抽象解释工具的缺陷检测能力.Heo 等人[60]还提出了一种资源敏感的分析方法,通过强化学习一个控制器来控制程序抽象的粗化程度,以在不动点迭代期间跟踪分析过程消耗内存等资源的情况,并动态调整其行为,使得在满足资源约束的条件下取得高精度的分析结果.
③提升抽象域分析效率.更高精度的抽象域,往往伴随着更高的时空开销.在当前的主要程序分析工具中,八边形抽象域和多面体抽象域表现仍然难以适应大规模分析,因而针对这2 种抽象域可扩展性的研究一直是热点话题.除了针对抽象域实现本身的优化[22-24]之外,有研究开始关注利用机器学习来加速抽象域分析.Singh 等人[61]提出了一种基于强化学习来加速静态程序分析的方法,在每次迭代过程中,利用强化学习来决策选择使用抽象域操作多种实现中的某一种,以实现分析精度和效率的均衡.He等人[62]提出了一种数据驱动的自适应学习方法,通过迭代学习算法来识别和删除分析过程中产生的抽象状态序列中的冗余状态约束,能够在提高现有数值程序分析效率的同时不会造成显著的精度损失.
3)提高可用性
实际中,待分析程序可能由不同程序语言实现,包含复杂数据结构,涉及各种不同程序特征.如何使抽象解释能够在实际中支持各种复杂数据结构与程序特征并取得较好效果一直是研究人员关注的话题.最近,应用抽象解释对特定类型程序或特定性质的分析验证方面的研究也取得了不少进展.主要包含4 个方面:复杂数据结构自动分析、不同谱系目标程序的分析、程序多种类型性质分析、编译场景下的应用.
在复杂数据结构的自动分析方面,在嵌入式代码中,动态数据结构(如列表、树)依赖于静态连续存储区域(数组)来实现,为此Liu 等人[63]提出了一种结合数组抽象和形态抽象的静态区域存储动态数据结构编程模式代码自动验证方法.其主要思想是基于对描述数组数值性质的谓词和描述动态结构形态性质的谓词这2 种谓词的元级合取,使得可以重用已有的对数组和动态结构单独分析的方法.该工作对嵌入式操作系统内核服务和驱动程序等包含复杂数据结构的实际程序的安全性质和功能性质进行了验证.此外,Journault 等人[64]提出了一种基于抽象解释的C 程序中字符串类型访问越界检测方法.
为提升抽象解释对形态相关程序的分析验证能力,Illous 等人[65-66]设计实现了关系型形态抽象域,并利用抽象形态迁移与基于分离逻辑的迁移摘要信息,设计了一种使用形态转换关系作为过程摘要的自顶向下的过程间分析方法.Li 等人[67]提出了一种基于状态剪影(silhouette)的抽象内存状态析取的合并策略,显著提升了形态分析的精度,并在形态分析工具MenCAD 中进行了实现.
随着概率编程的兴起,基于抽象解释的概率程序分析开始进入人们视野[68-69].相比确定性的静态程序分析,概率程序静态分析因递归、非结构化控制流、发散、不确定性和连续分布这些特征而更具挑战性.2018 年Wang 等人[68]提出了一个概率程序分析框架PMAF,用于设计实现概率程序的静态分析,并证明分析的正确性.在PMAF 框架中,Wang 等人[68]引入前马尔可夫代数(pre-Markov algebras)以分解出概率程序不同分析中的共同部分,并通过将传统(非概率)程序的过程间数据流分析思想扩展到概率程序分析中,以实现过程间分析和函数摘要生成.相比概率抽象解释[70-71](probabilistic abstract interpretation),PMAF具有2 大优势:一是其基于代数,为实现新的抽象提供了简单的声明式接口;二是其基于不同的语义基础,这些语义遵循域理论中对非确定概率程序的标准解释.
在操作系统代码的安全和功能性分析方面,抽象解释最近也得到了应用[63,72-73].2019 年Gershuni 等人[72]针对Linux 子系统eBPF(其允许在Linux 内核中运行用户编写的程序),通过使用Zone 抽象域跟踪寄存器和偏移间的差异,在抽象解释的框架下设计实现了一个针对eBPF 的静态分析器.该分析器相比现有的eBPF 静态分析工具拥有更低的误报率和更好的可扩展性,并支持对循环的分析.
在资源使用量上界分析方面,Carbonneaux 等人[74]提出了一种结合平摊分析与抽象解释的精确资源界分析方法,并设计实现了工具C4B.Fan 等人[75]提出了一种基于抽象解释的命令式C 程序中动态分配类型资源(如堆内存)使用量上界分析方法,通过对资源分配相关API 的资源使用建模,引入辅助变量刻画程序资源使用情况,然后结合数值抽象与指向分析,得到任意程序点处的资源使用量不变式.Facebook公司也在推进大规模程序的资源使用界分析[76],主要依托于程序分析工具Infer 中WCET 相关插件与数值抽象解释相关插件.
在编译相关技术方面,Rivera 等人面向浮点程序,设计并实现了浮点代码到基于区间算术代码的编译器IGen[77]和SafeGen[78].IGen 将基于浮点实现的C 函数转换为等效的使用区间算术的可靠C 函数,在保持较高精度的同时保证运行效率,提高了性能.在IGen 的基础上,SafeGen 将给定的浮点程序重写为相应的使用仿射算术的可靠程序,在保持变量之间线性相关性的同时,与区间算术相比实现了更高的精度.在ARM 指令集反汇编场景下,Ye 等人[79]设计实现了反汇编工具D-ARM,在解释指令的时候对指令执行过程中的具体值和执行过程的关键寄存器进行了符号化处理,并映射到抽象域上,为后续构建指令超集图提供语义信息.
2.2 工具进展
目前,抽象解释理论在程序分析与验证领域获得了广泛的研究和应用.表1 列出了目前主要的基于抽象解释的程序分析工具.
Astrée[5]作为抽象解释工具最典型的成功案例已经被广泛应用于空客公司的飞控软件的安全验证中[4].Astrée 能够支持对大规模现实程序的分析,并且误报率极低.这主要是因为Astrée 中集成了多种抽象解释分析优化技术,包括众多类型的抽象域、多种抽象域间的协同技术、迹划分技术、模块化分析技术等[4,95-96].
CGS(C Global Surveyor)[80]为NASA 内部使用的C 程序静态分析工具,它主要用于数组边界安全性检查;能够在几个小时内,以80%的精确度分析28 万行的火星任务飞行控制软件,并成功应用于Mars Path-Finder,Deep Space One 和Mars Exploration Rover等航天器的软件上.CGS 在一个增量式的框架内结合指针分析与数组下标的数值分析,分布部署到集群内多台机器上进行协同分析.
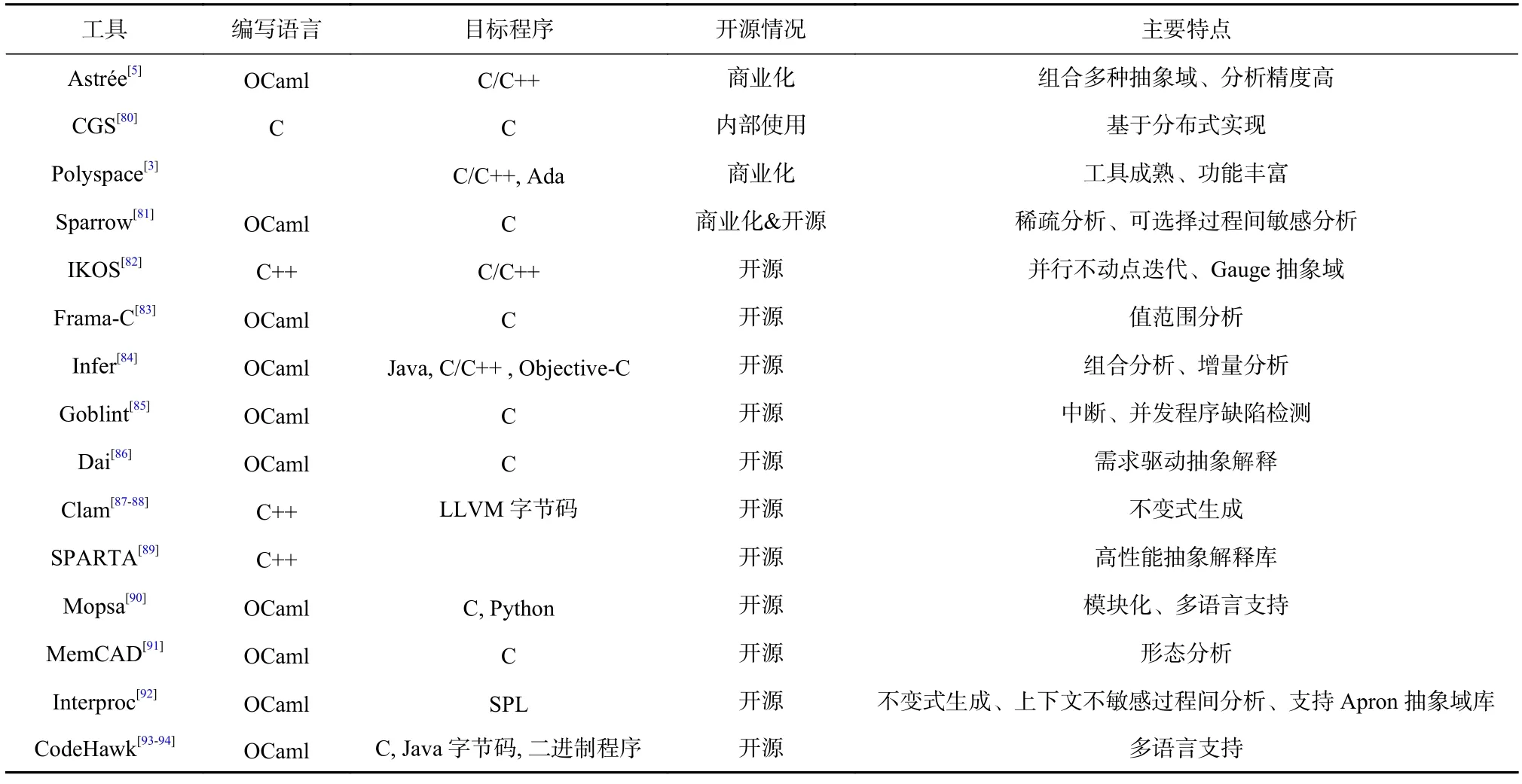
Table 1 Program Analyzers Based on Abstract Interpretation表1 基于抽象解释的程序分析工具
Polyspace[3]目前为Mathworks 公司旗下的商业化静态程序分析工具.Polyspace 可用于证明程序在所有的控制流和数据流下均没有关键的运行时错误.Polyspace 已被成功运用于M-346 教练机自动驾驶仪软件和沃尔沃汽车部分软件的安全验证中.
Sparrow[81]为韩国首尔国立大学开发的商业化C程序抽象解释工具,其同时存在开源版本.Sparrow采用了许多优秀的静态分析技术,以实现可扩展性、精确性和用户便捷性的统一.在可扩展性方面,Sparrow 使用了稀疏分析框架[97-98]等技术;在精确性方面,Sparrow实现了可选择的上下文敏感分析和可选择的关系型分析[99]等技术;而在用户便捷性方面,Sparrow 支持警报聚类[100]等技术.Sparrow 能实现对Linux 内核代码的高效分析验证.研究人员还利用机器学习技术,进一步提升Sparrow 的性能[59-60],并通过动静态结合的方法减少分析的误报[48].
IKOS[82]是最初由NASA 研究员发起的一款开源C/C++程序抽象解释工具.IKOS 已成功支持开源四轴飞行器软件AeroQuad 和开源无人机控制软件DIY AutoPilot 的分析验证.其主要特点包括其自主设计实现的Gauge 抽象域[101],以及最近基于并行计算和内存优化设计的高效不动点迭代算法[54,57].
Frama-C[83,102-103]为开源C 程序分析平台,包括多个实现不同功能的插件,其中包含了基于数值抽象解释的值分析插件EVA,且不同功能的插件可以互相配合以使得分析验证更加精确.Frama-C 已成功运用于巴西卫星运载火箭VLS-V03 控制软件、NASA空中交通管理系统的分析验证中.
Infer[84,104-108]是Facebook 公司开发的开源程序分析工具,并被用于日常的软件开发流程,以提升代码安全性.Infer 采用组合分析和增量式分析方法.Infer还集成了分离逻辑的实现,以达到更好的内存安全检测效果.此外,Infer 采用基于函数摘要的过程间分析方法以提升分析的效率.
Goblint[85]主要用于分析多线程程序,特别是用于检测中断并发错误.其支持数据竞争检测、断言检测、整数溢出等类型缺陷的检查.Goblint 结合指针分析与数值分析来处理动态分配和数组中的锁[109].Goblint 还将线程模块非关系值分析作为局部迹语义的抽象,并基于副作用约束系统以实现更通用、更精确的线程模块化分析[110].此外,Goblint 最近还对不动点求解算法进行了优化,以适应更大规模和更复杂程序的分析[111-112].值得注意的是,Goblint 是路径敏感的[113],并增加了对增量式分析[114]和交互式分析[115]的支持.
Dai[86]为开源C 程序抽象解释工具,其最大的特点是实现了需求驱动的抽象解释分析[13],使得程序分析能够交互式进行.
Clam[87]是开源的抽象解释静态分析工具,能分析LLVM 字节码并得到归纳不变式.其主要依托于Crab[88]构建.Crab 是一个服务于构建基于抽象解释的静态程序分析的开源基础库,采用C++实现.Crab提供了丰富的抽象域类型、不动点迭代算法的实现,并支持数据流分析、过程间分析和后向分析等类型的分析.
SPARTA[89]是Facebook 开源的一个软件组件库,用于构建基于抽象解释的高性能静态分析器.SPARTA 旨在提供拥有简单API、性能高、易于集成的软件组件,以简化抽象解释工具构建的工程量.由于SPARTA 对抽象解释复杂细节进行了封装,用户基于SPARTA 设计抽象解释工具时只需要关注于程序分析的3 个基本方面:1)语义,指待分析的性质,如数值型变量值范围、别名关系等;2)划分,指被分析性质的粒度,如过程内/过程间分析、上下文敏感/不敏感分析等;3)抽象,指程序性质的表示方法,如区间、别名图等.SPARTA 的成功应用是为Facebook开发的Android 字节码优化工具ReDex 中大多数的优化环节提供了分析引擎.
Mopsa[90]是一个基于抽象解释的静态分析通用框架.Mopsa 致力于通过模块化抽象,能够一次只对软件中的某个组件进行分析,从而在不降低精度的同时提升软件分析的效率.Mopsa 支持不同的迭代器和抽象,并能够支持不同类型语言的分析,尤其是支持动态类型语言Python 的分析,这也是其近期研究的主要关注点[116-118].
MemCAD[91]是开源的形态分析工具,主要用于分析、验证程序的内存使用相关性质,特别是链表和树等动态结构相关断言的验证.用户可以针对数据结构的描述来参数化选择工具使用的抽象域.
Interproc[92]是一个开源的抽象解释工具,可分析得到一种自定义的简单命令式语言SPL 编写的程序并得到数值变量的数值不变式.Interproc 支持包含递归在内的过程间分析[119].Interproc 由前端、开源的不动点求解库、开源抽象域库Apron 3 部分组成.
CodeHawk[92]是一个基于抽象解释的静态分析工具,由Kestrel Technology 公司开发并开源[94].其基于一种自 定义的 中间语言CHIF(CodeHawk internal form)实现了一个与目标程序语言相独立的抽象解释引擎,能够支持C、Java 字节码和二进制程序等3 种不同语言程序的分析.该抽象解释引擎包含了高效的迭代分析器,以及值集合、污点、多面体和区间等多种抽象域.CodeHawk 还通过分而治之的方法实现对大规模程序的分析[94].
总体而言,基于抽象解释的程序分析工具在最近几年的进展体现了3 个趋势:1)关注分析规模和效率的提升.利用并行计算、内存优化、机器学习等技术,提升程序分析工具的性能.2)多语言支持.大部分传统的分析工具只支持C 程序分析,而最近抽象解释工具增加了对并发程序,以及Java、Python 和二进制等程序分析的支持.3)与软件开发过程联系更加紧密.不同于传统的全程序分析,通过增量式分析、交互式分析和需求驱动分析,抽象解释分析工具能更好地适应软件迭代式开发、增量式演化等特点,以更好融入软件生产开发的全过程.此外,程序分析误报的消除也能进一步提升软件开发人员的使用友好度.
3 基于抽象解释的可信人工智能
本节主要介绍抽象解释在人工智能可信保证中的应用及其进展.
3.1 神经网络模型验证
近年来,深度神经网络(deep neural network,DNN)被广泛应用于安全攸关领域,包括自动驾驶系统、医疗诊断系统、飞行器防碰撞系统等.在此类系统中,可信性质被违背可能带来严重后果.如何确保神经网络系统的高可信性已成为人工智能技术在安全攸关领域广泛应用所面临的问题.神经网络验证是检验和提高神经网络可信性的重要手段.
神经网络可以看作是一类程序,因此可基于面向程序的形式化分析与验证技术研究其可信性.但神经网络又有其特殊性.例如,输入一般是高维的,且激活函数是非线性的,实际应用中神经网络包含的神经元数量往往非常庞大,故对神经网络进行精确推理代价很大.抽象解释技术通过对神经网络的具体语义进行抽象,使其能够在抽象语义上实现更加高效的推理.2018 年,Gehr 等人[120]提出了基于抽象解释的神经网络验证框架AI2,首次将抽象解释技术应用于神经网络的安全性和鲁棒性验证;使用带条件的仿射函数实现对ReLU 激活函数的抽象建模,在此基础上实现了面向神经网络验证的区间和Zonotope 及其幂集抽象域.此后,基于抽象解释的神经网络验证技术不断涌现.也有不少综述[121-123]介绍了基于抽象解释的神经网络验证方面的工作.2021年,Albarghouthi[124]详细介绍了基于抽象解释技术开展神经网络验证的典型算法和前沿工作.在神经网络验证领域,抽象域设计尤为重要,目前广泛使用的抽象域包括区间抽象域、Zonotope 抽象域和多面体抽象域等,它们有效实现了精度和效率的合理折衷.
3.1.1 基于区间抽象域的验证
在神经网络验证领域,区间抽象域技术在很多文献中被称为区间界传播(interval bound propagation,IBP)[125]或区间分析(interval analysis).Mirman 等人[126]将区间抽象域、区间界传播、区间分析等概念视为等价的,它们本质上都是抽象解释框架下的一种基于区间算术的抽象推导方式.为此,本文在描述上也不对这些概念进行刻意区分.此外需要说明的是,在程序分析领域,区间抽象域中的区间上界和下界一般是具体的实数,而在神经网络分析中,上界和下界可能是符号表达式(即符号区间),此时的符号区间实质上表示的是一个多面体抽象域,但当它基于输入值范围进行具体化后又会得到一个值区间,故又可称为区间抽象域.
区间分析最早在AI2中被用于神经网络验证[120].随后,Wang 等人[127]针对ReLU 神经网络提出了基于符号化区间的神经网络形式化验证技术,其主要思想是为每个神经元维持一个关于输入变量的符号区间,并逐层向后传播,当利用符号区间计算得到的神经元(执行激活函数前)取值范围包含0 时(即无法确定神经元激活状态),则用值区间替换符号区间继续向后传播,直至得到输出层的符号区间和值区间信息,并据此判断待验证性质是否成立.在逐层向后传播过程中,用具体值区间替换符号区间时会丢失神经元之间的依赖关系,从而造成输出层神经元的计算精度大量损失,可能导致性质无法得到有效验证.Wang 等人[128]对这一方法进行了改进,提出了基于线性松弛的符号化区间分析技术,其主要思想是为每个神经元维护2 个符号区间,一个记录激活函数处理之前的符号界信息,另一个记录激活函数处理之后的符号界信息.当神经元激活状态确定为激活或非激活状态时,激活函数之后的符号界信息可以精确得到;否则需要利用线性松弛技术(基于激活函数之前的神经元符号界和值范围信息)近似计算激活函数之后的符号界信息.这种传播方式既能够有效维护神经元之间的部分依赖关系,又能避免精确传播带来的组合爆炸问题,取得了更好的验证效果.Yin 等人[129]提出一个更精细的抽象域,在抽象表示上为每个神经元维护2 个符号区间、1 个值区间和1 个激活状态变量(可能取值是激活、非激活或不确定),在此基础上还在每遍抽象分析过程中显式记录一组输入变量必须满足的线性约束;在抽象迁移上,针对神经元激活函数状态非确定情形,提出了一种新的线性松弛技术,它能保证该神经元抽象传播过程中精度损失的面积达到最小,实验表明该抽象域在单遍分析精度以及基于分支限界(B&B)的迭代验证框架中均表现出了明显优势.
尽管抽象解释技术由于抽象带来的精度损失可能导致很多性质无法验证,但在神经网络验证实践中依然 取得了 很好的效果.Baader 等 人[130]、Wang 等人[131]从理论层面分析了其中的原因,他们一般化描述了神经网络的通用近似(universal approximation)性质,并将其应用于基于区间抽象域或者其他更精确抽象域的神经网络验证.具体而言,假定某个神经网络在给定输入区域内是鲁棒的,但基于区间抽象域却无法验证其鲁棒性时,Wang 等人[131]证明总能基于现有激活函数(ReLU,Sigmoid 等)构造一个新的神经网络,该网络可以在语义上按照需要无限接近于原来的神经网络,同时可以基于抽象解释技术验证这一新构建的神经网络在给定区域内是鲁棒的,从而在理论上证明了抽象解释技术可以验证任何神经网络的性质.但文献[131]中同时也指出构建新神经网络的复杂度在最坏情况下可能是NP 难的.Mirman 等人[126]也进行了理论分析,指出区间分析在验证分类神经网络的鲁棒性上是存在局限性的,并通过定理证明了并不是所有的神经网络都能够通过构造不可逆函数实现精确的区间分析.鉴于此,文献[126]中进一步推导出一个悖论:即使所有数据集都可以进行鲁棒分类,但仍然存在一些简单的数据集不能用区间分析来证明其分类的鲁棒性.这些研究从理论层面分析了抽象解释框架(特别是区间分析)的可用性和存在的一些局限性,对深入研究可信神经网络具有重要意义.
3.1.2 基于Zonotope 抽象域的验证
Gehr 等人[120]在AI2中将Zonotope 抽象域引入到神经网络验证领域.而后,Singh 等人[132]专门针对ReLU,Tanh,Sigmoid 激活函数重新设计了基于逐点传播的Zonotope 抽象迁移操作,有效减小了Zonotope投影到二维平面上的面积,从而提高了分析精度.基于重新设计的Zonotope 抽象域,开发了既支持串行迁移计算又支持并行迁移计算的神经网络验证系统DeepZ,并在MNIST 和CIFAR10 等数据集上开展实验,验证包含8 万多个神经元的神经网络的鲁棒性.实验结果表明DeepZ 相比之前的工作取得了更精确且更高效的验证效果.
为了进一步提高验证精度,Singh 等人[133]提出了一种基于精化的神经网络鲁棒性验证方法,其主要思想是充分利用抽象解释方法的高效性,以及混合整数线性规划和整数规划松弛技术的高精度,并采用启发式策略选取在抽象解释的上近似分析(如基于Zonotope 抽象域)过程中精度损失较大的神经元,对于这些神经元再利用整数线性规划和松弛技术计算更加精确的符号和值范围.基于该方法,实现了一个支持完备神经网络验证的工具RefineZono.实验结果表明,对于大规模神经网络,RefineZone 相比其他不完备验证工具拥有更高的精度;而对于小规模神经网络,在保证验证完备性的情况下,RefineZone 相比其他完备验证工具表现得更加高效.
最近,Jordan 等人[134]基于Zonotope 抽象域设计了一种新颖的算法ZonoDual.ZonoDual 有效结合了基于抽象域和基于最优化技术2 种方法来计算界信息,具有的特点为:具有高度可扩展性并且适合GPU加速;结合后的方法比单一使用某种方法能够获得更精确的界信息;方法具有高度可调节性,可以有效实现精度和计算效率的折衷;可作为一个附加组件加入到已有的对偶验证框架中来进一步提高其性能.在MNIST 和CIFAR10 等数据集上的实验表明,ZonoDual 算法在精度和效率方面都优于线性松弛技术,并且产生了比以前的对偶方法更精确的界信息.
3.1.3 基于多面体抽象域的验证
Singh 等人[135]将多面体抽象域应用于神经网络验证,设计了一种新的抽象域表示,即针对每个神经元分别维护1 个符号区间和1 个值区间,提出了新的抽象迁移函数处理仿射转换、ReLU、Sigmoid、Tanh、Maxpool 等神经网络中的常见算子.此外,还基于多面体抽象域实现了一个验证工具DeepPoly,并在MNIST和CIFAR10 数据集上开展实验,结果表明DeepPoly能够有效验证卷积神经网络在无穷范数和旋转扰动下的鲁棒性.Tran 等人[136]提出了一种称之为ImageStars的卷积神经网络集合表示方法,其实质上是多面体抽象域的另外一种刻画方式,文献[136]将ImageStars应用于基于集合的分析框架中,并分别设计算法实现卷积层、全连接层、最大池化层、平均池化层可达状态的精确和上近似计算.进一步基于该可达性分析算法实现了神经网络验证工具NNV,并在实际中广泛使用的卷积神经网络VCG 上开展实验.结果表明NNV 工具相比DeepPoly 能够更好验证VCG 在对抗攻击(如DeepFool 攻击)下的鲁棒性.Goubault 等人[137]结合基于集合的方法和抽象解释技术,提出了一种使用Tropical 多面体抽象ReLU 前馈神经网络的方法.文献[137]中阐述了Tropical 多面体可以有效地抽象ReLU 激活函数,同时又能够较好控制由于线性计算而导致的精度损失.
为了实现更大规模神经网络的验证,Müller 等人[138]在GPU 上设计了面向神经网络验证的通用、可靠的多面体抽象域的算法.该算法充分利用了GPU 的并行处理能力以及神经网络验证问题固有的稀疏性,并在此基础上实现了一个可扩展性高的基于多面体抽象域的并行验证工具GPUPoly.实验表明GPUPoly能够在34.5ms 时间内验证包含30 多个隐含层、上百万个神经元的深度残差网络的鲁棒性,使得抽象解释技术朝验证现实世界超大规模人工智能系统迈出关键的一步.
大部分非完备的验证技术都是基于单个神经元的凸抽象,即对隐含层的每个神经元的抽象都是单独进行的,对该隐含层的抽象则是每个神经元抽象结果的并,在几何上即每个神经元的凸闭包的笛卡尔乘积.从单个神经网络隐含层抽象角度来看,这种抽象方式精度显然会低于该隐含层的最优凸闭包,更重要的是它忽略了同层神经元之间的依赖关系,且这种抽象方式的精度损失会在神经网络逐层推导过程中被不断放大,从而导致输出层的分析精度十分受限.Salman 等人[139]阐明了单个神经元凸抽象的固有局限.为了消除该局限,有工作[140]针对ReLU 网络提出了多神经元抽象技术,相比单个神经元的凸抽象,其精度更高;而相比最优凸闭包,它又具有更好的可扩展性,因此可看作最优凸闭包和单个神经元凸抽象的一个折衷方案.
Singh 等人[137,140]提出了k-Poly 的方法,其要思想是将隐含层的神经元划分为若干个(集合元素数目小于等于5)小集合,再将每个小集合的神经元分为若干个组,每组神经元数量不超过k个(k≤3),对于每组神经元通过八面体[141](octahedra)抽象域来对其输入进行刻画,在此基础上联合计算该组k个神经元的最优凸闭包输出.最优凸闭包的计算代价非常高,并且会产生复杂的输出约束,因此只会应用在少数几个互不相交的神经元组上,这就限制了该方法能够维持的同层神经元之间的依赖关系数量.
Tjandraatmadja 等人[142]和Palma 等人[143]在考虑隐含层的输入时,将激活函数与激活函数之前的仿射层合并得到一个多维激活层,并计算多维激活层的凸近似,以得到该隐含层的一个超盒(hyperbox)近似.这种粗略的输入抽象一定程度上缓解了只在单个仿射层上进行近似的缺陷.实验表明,文献[142-143]的方法都取得了较好的精度提升,但它们仅限于ReLU 激活并且缺乏可扩展性,原因是需要精确计算少量神经元的最优凸闭包或者大量神经元的较优凸闭包.此外,它们也没有解决如何在层内获取足够的神经元相互依赖关系以尽可能接近最优凸抽象的问题.针对这些问题,Müller 等人[144]提出了PRIMA验证框架,它能处理包含ReLU,Sigmoid,Tanh,MaxPool等多种激活函数的神经网络.PRIMA 是建立在k-Poly基础上的,它通过考虑大量相对较小的重叠神经元组,获得神经元之间的大多数相互依赖关系.虽然它没有达到最优凸闭包的精确程度,但相比以往的抽象技术,PRIMA 在逐层推导过程中获得了显著的精度提升.实验表明,PRIMA 在自动驾驶领域的真实神经网络上实现了精确验证,而且时间开销控制在几分钟以内.
3.1.4 结合抽象解释的验证精化
抽象解释在上近似过程中会引入精度损失,从而可能导致分析结果精度不足以支撑神经网络性质的验证.Li 等人[145]和Yang 等人[146]研究提出了一种基于符号传播的方法来提高基于抽象解释的神经网络验证的精确性,并将精化后的神经元的边界值信息用于提高基于SMT 的神经网络验证方法(如Reluplex)的性能.Elboher 等人[147]提出类似反例制导抽象精化(CEGAR)的神经网络迭代验证技术,其主要思想是将神经网络进行可靠抽象得到一个较小规模的网络,并在该网络上进行性质验证,如果性质成立则终止验证;否则生成一个反例,用于指导神经网络抽象,从而得到一个更大的、更接近于原始网络的新网络,并在新网络上重新展开验证.
另一个主流的精化方式是将抽象解释分析技术与基于搜索或最优化的技术相结合[148-151],从而实现更加精确的验证,更多相关工作请参见综述文献[121].本文重点介绍基于分支限界(branch and bound,B&B)方法,它也是一种结合搜索和抽象分析的通用迭代验证框架[152-153].该框架包括2 个关键过程,即Branch 过程 和Bound 过程.Bound 过程是 指通过分析获取神经网络各个隐含层和输出层神经元的界信息,快速判断待验证性质是否成立.为了保证整个验证框架能够高效工作,界信息的获取通常在抽象语义下(如基于抽象解释、区间传播、线性松弛等技术构建神经网络的上近似抽象)进行,以尽量提高每遍Bound 过程的效率.Branch 过程是指当Bound 过程产生的界信息尚不足以验证其性质时,通过划分技术,将原来较难验证的问题分解为若干更易于验证的子问题,针对每个子问题再通过Bound 过程判断性质是否成立.如果所有子问题都得到成功验证,则说明待验证性质成立;否则如果在某个子问题中找到反例,则说明待验证性质不成立.B&B 框架提供了一个思路,使得原本不完备的抽象解释技术能够实现完备的神经网络验证.事实上,当前不少工作[154-156]都可以归结为B&B 框架的一个应用,只是设计了不同Bound 算法和Branch 算法.Wang 在文献[157]中系统介绍了B&B 技术在神经网络验证领域取得的主要进展.
这里重点介绍3 个工具,即ReluVal[127],Neurify[128]和LayerSAR[129].这3 个工具都在B&B 框架下实现更加完备的验证,其主要思想都是利用了抽象解释技术计算抽象可达状态集合(即Bound 过程),并同时采用基于输入域划分的迭代技术(即Branch 过程)不断精化抽象可达状态集合,从而最终达到验证性质的目的.具体而言,ReluVal[127]采用了基于二分法的输入域划分技术,即直接在输入空间上启发式选取1 个输入变量,再对该变量的区间值范围进行均匀二分,从而得到2 个子输入空间,再针对每个子空间开展迭代抽象验证,文献[127]基于利普希茨连续性定理证明了二分法在理论上是完备.基于二分法对输入域划分的优点是操作简单、易于实现,但缺点也十分明显,即划分的目的不清晰、具有盲目性,从而导致提升验证效率的效果不佳.为了克服这些不足,Neurify[128]结合了符号化线性松弛技术和基于中间层神经元的输入域划分技术.其划分神经元的选取策略是在预分析阶段基于梯度分析技术反向推导每个隐含层神经元对性质验证的影响程度,在迭代阶段则根据分析结果依次选取影响程度更大神经元作为划分对象.Neurify 在一定程度上提高了验证效率,但由于划分神经元可能来自任意隐含层,故在前向抽象分析得到的符号上下界可能不相等.由此带来的问题是当每个神经元最多被划分1 次时(Neurify 工具在实现上基于如此假设),它的划分技术不能保证该验证方法能够经过有穷迭代后得出完备的验证结论.针对Neurify 可能不完备的问题,LayerSAR[129]提出了基于非确定首层(FUL)的划分策略.FUL 是指从(输入层到输出层)逐层抽象分析过程中首个包含神经元激活函数状态非确定的隐含层.FUL 层神经元具有的性质为符号上界和符号下界总是相等的.故在划分后得到的2 个子验证问题中划分神经元的激活状态都会变得确定化,从而能够证明每个神经元至多划分1 次即能验证性质成立.此外,LayerSAR 进一步利用划分谓词对输入域进行精化,从而进一步提升单遍抽象解释分析精度.
3.1.5 在RNN 验证上的应用
3.1.1~3.1.4 节所述的基于抽象解释的神经网络验证工作大多聚焦于检验全连接前馈神经网络(FFNN)和卷积神经网络(CNN)的安全性和鲁棒性等可信性质.近年来,随着形式化方法逐步应用于循环神经网络(RNN)的验证[158-164],抽象解释技术也发挥了越来越重要的作用[158,160,162].
Zhang 等人[158]在深入分析并定义认知领域RNN需要验证的重要性质的基础上,提出了一种新的RNN 性质验证方法.该方法主要包括2 个阶段:一是改进“易于验证的网络”范式,并用于训练循环网络;二是结合混合多面体传播、多面体不变式生成和反例制导的抽象精化等技术进行RNN 性质验证.在上述验证过程中,应用了抽象解释框架下凸多面体有穷幂集抽象域,并设计了专门处理多面体的凸闭包的抽象函数和降低凸闭包精度损失的精化函数,以解决具体语义下可达性分析中多面体数量呈指数增长的问题,以及如何获得足够的抽象分析精度来证明所需验证的性质等.实验结果表明,该工作中采用的技术为应对这些挑战提供了可行的解决方案.
Akintunde 等人[159]和Jacoby[160]等人分别采用不同的方法将RNN 验证问题转化为FFNN 验证问题,再借助已有的包括基于抽象解释技术在内的任意形式化验证工具对转换之后的FFNN 开展验证.这些方法不同之处在于文献[159]采用的转换过程是对RNN 进行有穷次复制(类似于程序分析中的循环展开技术),故最终实现的是一种不可靠(unsound)的部分验证;而文献[160]的转换过程采用了一种基于不变式的上近似技术(类似于抽象解释技术处理程序中的循环),其核心思想是把RNN 传播过程中上一时刻的记忆单元值使用含时间变量t的线性归纳不变式(实质是一个符号区间约束)进行可靠抽象,从而避免了RNN 展开技术导致的网络规模急剧增大的问题.当经过抽象的FFNN 不足以验证原来性质时,可通过精化关于t的线性归纳不变式进行不断迭代,最终实现高效可靠的RNN 神经网络验证.
Ryou 等人[162]实现了一个可扩展的、高精度的递归神经网络验证工具Prover,其主要思想为:结合采样技术、优化技术和费马定理,设计一系列多面体抽象方法,以计算非凸和非线性的递归更新函数;提出了一种基于梯度下降的抽象精化算法,该算法针对待验证的性质,结合了每个神经元的多种抽象方式.基于Prover,文献[162]中研究了语音识别领域RNN非平凡应用实例的验证问题,并设计实现了非线性语音预处理管道的自定义抽象方法.实验表明,Prover 能够成功验证计算机视觉、语音和运动传感器数据分类和识别中若干个极具挑战性的,且在此之前的工作都未能处理的RNN 网络模型.
3.2 神经网络模型鲁棒训练
神经网络可信性验证总是假定待验证的神经网络是已经训练好的,而神经网络的可信训练则是研究如何在神经网络训练过程中针对特定属性提高其可信性.目前,有不少研究工作都使用抽象解释技术训练更鲁棒的神经网络.实践证明,基于抽象解释训练得到的神经网络在对抗扰动攻击上表现出了更好的鲁棒性,反过来这种鲁棒性也更易于通过抽象解释技术得到验证.
Mirman 等人[165]和Gowal 等人[166]最早于2018 年将抽象解释应用于神经网络训练过程.文献[165]提出了可微抽象解释(differentiable abstract interpretation)技术用于训练大规模神经网络,从而保证训练出来的神经网络总是满足某些鲁棒性质.在此基础上,Fischer 等人[167]提出了一种面向深度学习的可微逻辑(differentiable logic),开发了系统DL2,并在无监督学习、半监督学习、有监督学习等场景下的神经网络可信训练上取得了较好效果.
此外,还有很多研究使用抽象解释技术训练更加鲁棒的图形识别和自然语言处理神经网络模型[168-172].文献[168]提出了一种通用语言,用于刻画与自然语言处理相关的可编程字符串操作(例如插入、删除、替换、交换等).在此基础上,提出了一种对抗训练神经网络模型的方法A3T,使得训练得到的模型关于用户指定的字符串操作是鲁棒的.A3T 充分结合了基于搜索的对抗性训练技术和基于上近似的抽象技术各自的优势.具体而言,文献[168]中介绍了如何将一组用户自定义的字符串操作分解为2 个组件规约,一个能够受益于搜索技术,另一个能够受益于抽象技术.使用A3T 在AG 和SST2 数据集上训练模型的实验结果表明,A3T 生成的模型对于用户自定义的模仿拼写错误和其他保留含义的操作都是鲁棒的.
文献[169]提出了一种用于训练鲁棒RNN 的方法ARC,并在LSTMs,BiLSTMs 和TreeLSTMs 等模型上展示了ARC 的有效性.ARC 是抽象解释技术的一个新的应用,以符号化方式刻画以编程方式定义的字符串集合,并通过RNN 进行传播.实验结果表明,相较于此前技术,ARC 训练出的模型对于任意空间扰动表现出更好鲁棒性.此外,ARC 能够证明给定神经网络模型关于某些攻击操作是鲁棒的,而此前技术很难做到这一点.
3.3 深度学习程序的分析
深度学习程序中含有大量的数值操作,因此难以通过测试的方法遍历所有的程序状态以检测出所有的程序缺陷.而静态分析能够考虑程序所有可能的状态空间,从而可以分析验证深度学习程序的可靠安全性.
不同于模型层面的神经网络验证方法,面向神经网络框架(如TensorFlow 编写的程序)的分析方法能够在模型训练前分析检测程序可能存在的缺陷.Zhang 等人[173]提出了一种神经网络框架层面的基于抽象解释的数值缺陷检测分析方法.该方法对神经网络架构分析时基于2 种抽象:一是张量抽象,二是数值变量的区间范围抽象.同时,其还通过张量划分和仿射等式关系抽象技术,在保证分析效率的同时提升分析精度.
4 抽象解释的其他典型应用
本节主要介绍抽象解释在其他方面的典型应用及其进展.
4.1 智能合约可信保证
以太坊智能合约的执行需要消耗gas.在智能合约部署运行前,通过静态分析的方法提前预估合约可能的gas 资源使用量峰值,有助于避免经济损失.为此,Pérez 等人[174]提出了一种基于抽象解释的参数化资源分析方法.此外,Grech 等人[175]提出了一种gas 泄漏检测方法,结合基于控制流分析的反汇编和声明式程序结构查询技术,在EVM 字节码上使用抽象解释进行分析,并设计实现了工具MadMax.
由于智能合约一旦部署便难以修补漏洞,因而对智能合约的安全性进行验证具有重要意义.Kalra等人[176]利用抽象解释、符号模型检验和带约束霍恩子句(constrained Horn clauses,CHC)的结合来快速验证合约的安全性,并构建了ZEUS 验证平台.文献[176]提出了Solidity 智能合约执行语义的形式化抽象,计算数据域上的循环和函数摘要,从而减少模型检验阶段的状态空间.ZEUS 对超过22.4 万个智能合约进行了评估,其误报率较低且没有漏报.
4.2 信息安全保证
在信息流安全无干扰性分析方面,Giacobazzi 等人[177-179]基于抽象解释引入了抽象无干扰性(abstract non-interference)的概念作为无干扰性概念的一般化.文献[177-179]指出抽象无干扰性是参数化的,以人们要保护哪些隐私信息、外部观察者可观察信息为参数,并指出可在标准的抽象解释框架内对抽象无干扰性进行刻画,使得程序的安全程度成为程序语义的属性.最近,Mastroeni 等人[179]设计了一个基于抽象解释的静态分析器,以可靠地检查无干扰性.文献[179]定义了一个超抽象域用于分析超性质(hyperproperty),它能够对被分析程序中出现的信息流进行近似.
针对Cache 侧信道泄漏问题,Köpf 等人[180]提出了一种基于抽象解释的量化方法,它通过静态Cache分析技术实现对抽象Cache 状态具体化后具体状态的计数,将静态Cache 分析与定量信息流分析结合,从而自动推导出攻击者通过观察CPU Cache 性能的方式从程序中提取关于输入信息量的上界.Doychev、Köpf 等人[181]还进一步开发了针对Cache 侧信道攻击的具有形式化且量化安全保证的开源静态分析工具CacheAudit,通过抽象计算攻击者可能的侧信道观测信息的精确上近似.Barthe、Köpf 等人[182]在此基础上将CacheAudit 应用于并发环境下的内存侧信道安全保证中.Doychev 和Köpf[183]进一步支持了动态内存分配环境下内存访问的位级推理和算术推理,使得能够针对可执行代码侧信道攻击软件防御措施开展严格分析.此外,Wang 等人[184]设计实现了一个秘密增强符号抽象域,并在此基础上提出了一种新的二进制静态分析方法来检测基于缓存的侧信道.Touzeau 等人[185]则通过结合抽象解释与模型检验,实现高效精确的缓存分析.
针对时间侧信道问题,Wu 等人[186]提出了一种基于程序分析和转换的方法,用于消除安全关键应用程序中的时间侧信道,这一方法借助了抽象解释实现的静态Cache 分析.Blazy 等人[187]实现了一种静态分析技术,它能够基于抽象解释技术,在源代码级别保证软件的实现是常数时间的.
对于在支持预测执行的处理器上运行的程序,分析它们的行为对于执行时间估计、侧信道检测等应用至关重要.然而,现有的基于抽象解释的静态分析技术没有对预测执行进行建模,因为它们关注的主要是程序的功能属性,而预测执行并不改变其功能.为此,Wu 等人[188]引入了虚拟控制流的概念,以及处理合并与循环的优化方法,并安全地限制预测执行深度,使得能够提升现有的抽象解释技术以支持分析预测执行下的程序.在静态缓存分析工具中使用该技术后,能够检测出许多被现有不支持预测分析技术所忽略的缓存泄漏和侧信道泄漏缺陷.
2021 年,Fang 等人[189]提出了一种零知识静态分析方法,它允许不受信任的一方在不暴露程序的情况下证明程序具有某种特性,并在抽象解释程序分析的基础上应用该技术.该工作提供了一种技术手段,能够打破分析工具难以接触受保密程序的现状.
4.3 量子计算可信保证
由于量子计算难以模拟,为理解更大规模的量子程序并检测断言,Yu 等人[190]将抽象状态视为一组投影构成的元组(通过投影来对密度矩阵进行近似),在此之基础上提出了构成伽罗瓦连接的抽象化函数和具体化函数,并使用它们来定义抽象操作.该工作提出了一种量子程序的抽象方法,并基于该方法实现了在多项式时间内支持300 个量子位的断言检测,这超出了当前超级计算机能够模拟的量子位数量.
5 未来研究方向展望
作为程序语言与形式化方法领域中的一个传统方向,抽象解释持续受到学术界和工业界的关注.目前来看,抽象解释在未来研究中的潜在方向包括:
1)结合上近似与下近似抽象的抽象解释.目前,绝大部分抽象解释技术采用的是上近似抽象,以保证分析验证的可靠性.然而,单纯采用上近似抽象可能导致精度不够,从而可能产生误报.研究下近似抽象,以及上近似与下近似抽象的结合,对于消除静态分析误报具有重要意义.结合O'Hearn 最近提出的不正确性逻辑[49],在抽象解释框架下研究下近似及其与上近似抽象的结合,是未来值得关注的研究方向.
2)机器学习辅助的抽象解释.抽象解释本身是基于形式化的,但是有效的启发式信息对于提高基于抽象解释的分析验证的精度、效率具有重要帮助.比如,约束模版的设置、加宽阈值的选择、抽象域的选择、变量打包的策略、控制流汇合操作的精度控制等,都依赖于启发式规则或者人工设定.而利用机器学习得到有效的启发式信息,对于更有效地面向具体应用来权衡抽象解释的精度和效率具有重要意义.
3)抽象域的析取表达能力提升.抽象域是抽象解释框架下的核心要素.但是,目前数值抽象域在表达析取信息方面存在局限性,导致分析精度不够.而实际程序中天然存在很多析取行为,设计能够表达析取的抽象域或者通用的析取表达能力提升算子,可以有效缓解传统数值抽象域的凸性局限性、提高程序分析的精度、减少误报.比如,将数值抽象域与SMT 约束求解器、决策图或决策树结合,可提升析取表达能力.
4)面向人工智能实际应用可信保证的抽象解释.目前抽象解释技术已经在深度神经网络模型和架构的分析与验证中有初步应用.但是目前实验对象的神经元规模离大部分实际场景下神经元规模有较大距离,支持的网络模型的类型也不够丰富;同时,如何应用抽象解释对实际场景中符号神经混合系统开展建模、抽象与分析验证也是值得关注的方向;另外,利用抽象解释进行实际应用中神经网络的鲁棒训练也值得更多的关注.
5)面向代码演化的抽象解释.持续集成、持续交付、持续部署已成为现代软件开发的“最佳实践”,被广泛应用于实际软件项目开发中.目前,抽象解释方法主要应用于完整程序代码的分析,而针对完整版本的分析过程往往需要较多的时间和资源开销,使其难以在快速迭代、持续集成等现代软件开发实践中快速响应.以快速迭代、持续集成等现代软件开发实践背景下所形成的系列代码版本、代码提交片段、版本合并等作为分析对象,形成具有支持代码演化的增量式抽象解释方法具有重要的现实意义.
6 结论
抽象解释是程序语言与形式化方法领域的一个重要的研究方向.本文系统地对近5 年来抽象解释的理论及其应用研究进展进行综述.首先介绍了抽象解释的基本概念并综述了其在理论框架、抽象域方面的最新进展;然后,重点概述了基于抽象解释的程序分析、基于抽象解释的神经网络模型验证与鲁棒训练及深度学习程序的分析等方面的研究进展;还对抽象解释在智能合约可信保证、信息安全保证、量子计算可信保证等方面的应用进展进行了介绍;最后对未来的研究方向进行了说明.总之,随着抽象解释理论、技术与工具的不断发展,未来抽象解释将在更多应用领域发挥越来越重要的作用.
作者贡献声明:陈立前负责论文总体设计、文献调研、理论进展与未来研究方向展望相关内容撰写;范广生负责程序分析与其他典型应用相关的文献调研与内容撰写;尹帮虎负责可信人工智能相关的文献调研与内容撰写;王戟提出指导意见并修改论文.
