基于VMD-ELM的农产品期货价格分解集成预测模型

张大斌, 曾莉玲, 凌立文

(华南农业大学 数学与信息学院,广东 广州 510642)

0 引言

农产品期货价格时间序列的准确预测不仅能够指导农业生产和经营，而且为政府辅助决策提供依据。因受多种因素，如外部市场、金融投机、国际形势等影响，农产品期货市场价格呈现出复杂的波动性、非线性特征，是一种典型的复杂时间序列，其准确预测极具挑战性。

在复杂时间序列预测建模领域中，分解集成方法论被视为是一种有效的提高预测精度的策略，其核心思想是利用信号分解算法将复杂的时间序列分解为一系列相对简单且平稳的子序列，以此降低建模工作的复杂度[1]。相比于其他分解模型，如小波分解(Wavelet Transform, WT)、经验模态分解 (Empirical Mode Decomposition, EMD)[2,3]，变分模态分解(Variational Mode Decomposition, VMD)作为一种完全内在、自适应非递归的分解技术，可以更为有效的捕获时间序列的波动特征，从而提高预测精度，在能源、有色金属等众多领域已经得到广泛应用[4,5]。例如，Liu等将LSTM网络结合EMD、VMD构建集成预测模型，选择有色金属价格作为对象，结合VMD分解技术的集成模型预测性能更优[6]。在农产品价格预测领域中也有相应的运用，例如，Wang分别将反向传播神经网络(BPNN)结合EMD、VMD、WT和STL分解，选择三种期货价格进行实验，所有混合模型与分解技术相结合均具有比单个模型更好的性能，VMD在提高预测能力方面贡献最大[7]。

尽管众多研究表明VMD分解具有较优的性能，但其分解效果受关键参数模态数K值的影响，即分解过多或不足都会影响分析结果的准确性[8]。因此在分解前选择适当的K值，是VMD广泛应用的关键。针对K值选取的难题，Zhang等使用VMD对风速时间序列进行分解，并且通过计算重构后序列的样本熵(Sample Entropy, SE)优化分解K值[9]。然而，样本熵采用二值函数度量相似度，且不计算自身匹配的统计量，因此容易产生不准确或无定义的样本熵[10]。基于此，本文在样本熵的基础上，引入模糊熵(Fuzzy Entropy, FE)优化VMD分解，获得适当的模态数K。与样本熵的二值函数相比，使用模糊隶属度函数进行相似性的度量，其模糊边界测量，能够提高对信号复杂度的评估，使得熵值的变化更加连续平稳[11]。由于模糊熵反映了时间序列的复杂度，因此当时间序列受到干扰，其状态值的不确定性增加时，熵值会相应地增加。

上述优化VMD分解得到不同尺度的子序列以后，需要选择有效的预测模型，适应不同尺度的时间序列预测。极限学习机(Extreme Learning Machine, ELM)由于无需多次迭代调整神经网络权值，学习过程仅需计算输出权重，强大的学习速度和泛化能力，能够有效捕捉VMD分解得到的不同尺度子序列的波动特征，已经在农产品价格预测中得到广泛应用[12]。本文选择ELM对VMD分解得到的子序列进行预测，集成得到最终预测结果。选取CBOT交易所的小麦、稻谷和豆粕期货价格作为实证对象，构建VMD-ELM的分解集成预测模型，实验验证了所提出的分解集成预测模型的有效性。

1 相关方法

1.1 变分模态分解

就时间序列分解算法而言，奇异谱分解(Singular Spectrum Analysis, SSA)是一种时域和频域相结合的非参数方法，能够有效提取时间序列中的主要成分，具有适用性广泛且操作灵活的优点[13]。互补集合经验模态分解方法(Complementary ensemble empirical mode decomposition，CEEMD)因能在一定程度上抑制了EMD分解中存在的模态混淆、端点效应等问题，因此广泛用于序列分解领域[14]。VMD分解是Dragomiretskiy等于2014年提出一种新型分解方法，其不仅计算效率高，且在解决信号噪声和避免模态混淆的问题上具有优势[15]。VMD分解通过设置合理的预设模态数K，将原始时间序列x(t)分解成K个模态函数uk，算法步骤如下：

(1)对于模态uk，通过Hilbert变换计算相应解析信号，从而获得单边频谱，随后加入指数项调整各自的中心频率ωk，将每个模态函数的频谱调制到基带，使得uk的有限频带围绕着其中心频率ωk，对已解调信号应用高斯平滑估算相应的带宽，使得带宽之和最小，故将受约束的变分模型构造为:

(1)

式中，t为时间，δ(t)为单位冲击函数，uk为分解模态，wk为模态对应的中心频率，约束条件为∑kuk=f(t)各模态之和等于原始信号f(t)。

(2)引入二次惩罚因子α和拉格朗日乘子λ，将变分问题转化为无约束优化问题:

L({uk},{wk},λ)

(2)

(3)使用拉格朗日函数将其从时域转化到频域，并计算相应的极值，模态分量uk及其中心频率wk的求解表达式如下:

(3)

(4)采用交替方向乘子法(ADMM)交替更新，将原始信号分解为K个窄带模态分量，得到约束变分模型的最优解。

1.2 极限学习机

(4)

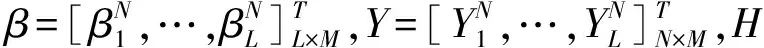
2 VMD-ELM分解集成预测模型

2.1 利用模糊熵优化VMD分解模型

针对VMD分解模态数K值选择的难题，本文利用模糊熵优化VMD分解模型，模糊熵的具体计算过程如下：

(4)因此，定义模糊熵FE(m,n,r,N)=lnφm(n,r)-lnφm+1(n,r)。

FE的计算与m,n,r这几个参数有关，通常嵌入维数m取2，此时计算量较小且对序列的变化更敏感；相似容限度r不宜过大，一般取r=0.2*std，std为序列的标准差，n取常用值1。由于模糊熵能度量时间序列的复杂度，基于此，基于最小模糊熵准则优化VMD分解模态数K值的方法具体步骤如下：首先，给定K=3,4,…,14，使用VMD模型将原始时间序列x(t)(t=1,2,…,N)自适应地分解为K个不同尺度的IMF分量序列集{Ii(t)}(i=1,2,…,K)。其次，计算IMF分量序列集{Ii(t)}模糊熵并排序，定义模糊熵最小的IMF分量为趋势项，其他IMF分量为随机干扰项。最后，比较不同分解K值下趋势项的模糊熵，以便获得适当的分解次数，当K值较小的时候，趋势项的模糊熵很大，随着K值的增加，模糊熵逐渐趋于稳定。因此，为了避免过度分解，将模糊熵趋于稳定的转折点作为VMD分解的模态数K。

2.2 分解集成预测框架与步骤

本文构建的VMD-ELM分解集成预测模型结构框图如图1所示:

图1 VMD-ELM分解集成预测模型

其具体建模步骤如下：

步骤1K值优化：计算在不同VMD分解模态K下趋势项的模糊熵，根据最小模糊熵准则确定分解的最优参数K值。

步骤2时序分解：确定最优K值以后，使用VMD模型将原始时间序列自适应地分解为K个IMF分量序列集{Ii(t)}(i=1,2,…,K)

步骤3集成预测：利用ELM模型对IMF分量中的趋势项和随机干扰项进行训练和预测，得到IMF分量的预测值si={s1,s2,s3,…,sK} ，线性相加si得到最终预测结果。

3 实证

3.1 数据描述

选取CBOT交易所的小麦、稻谷、豆粕期货收盘价作为样本数据，该样本数据涵盖了2013年1月到2020年9月期间的的周度价格，共398个观测值，图2显示了小麦、稻谷、豆粕的周度价格曲线。选取样本数前80%的数据作为训练集，后20%的数据作为测试集。

图2 农产品价格周度曲线

3.2 评价准则

3.3 实验过程

3.3.1 优化VMD分解模型

为了验证基于模糊熵的K值优化法的有效性，计算VMD分解不同K值条件下的样本熵和模糊熵，图3～4展示了样本熵和模糊熵的变化折线。可以看出，除了豆粕以外，其余农产品的样本熵在一定范围内并未趋于稳定，而是处于大幅度波动变化的，且豆粕的样本熵和模糊熵的变化情况相似，而三种农产品的模糊熵均在一定范围内趋于稳定，因此利用最小模糊熵准则对VMD分解的K值进行优化，根据图4可以看出，具有不同K值的趋势项的模糊熵结果如下：对于稻谷期货，当K超过11的时候，模糊熵趋于稳定，因此利用VMD对稻谷期货进行分解得到11个模态分量。对于小麦期货，当K超过10的时候，模糊熵趋于稳定，因此利用VMD方法对小麦期货进行分解得到10个模态分量。同理，对于豆粕期货，当K超过10的时候，模糊熵趋于稳定，因此利用VMD对稻谷期货进行分解得到10个模态分量。

图3 农产品价格VMD分解不同K值下的样本熵

图4 农产品价格VMD分解不同K值下的模糊熵

3.3.2 VMD分解价格序列

通过以上分析确定合适的VMD分解模态数K，对稻谷、小麦、豆粕期货价格进行分解。图5表示了通过VMD分解原始稻谷、小麦、豆粕数据获得的子序列，图中，IMF1是趋势项，其余IMF是随机波动项。因此，可以通过预测模型研究农产品价格数据中具有不同特征的子序列。

图5 农产品价格VMD分解结果

3.3.3 预测建模

图6 农产品价格VMD分解子序列预测结果

对IMF的分解结果进行线性相加，得到最终预测值，图7显示了六种不同模型的稻谷、小麦、豆粕期货预测曲线。其中，黑色实现表示实际观测值，由图可知，单模型ELM预测结果不稳定，与实际观测值拟合程度最差，集成模型相比于单模型更加接近实际曲线，特别地，所提出的集成预测模型VMD-ELM非常接近实际观测值。

图7 不同模型预测农产品价格拟合曲线

3.4 结果分析

3.4.1 VMD-ELM预测效果的比较分析

为验证所提出的VMD-ELM分解集成预测模型的预测性能, 统计并且比较分析ELM、VMD-ELM、SSA-ELM、CEEMD-ELM模型在农产品期货市场价格的预测结果，获得的预测误差对比如表1所示，黑色加粗表示最优误差值。

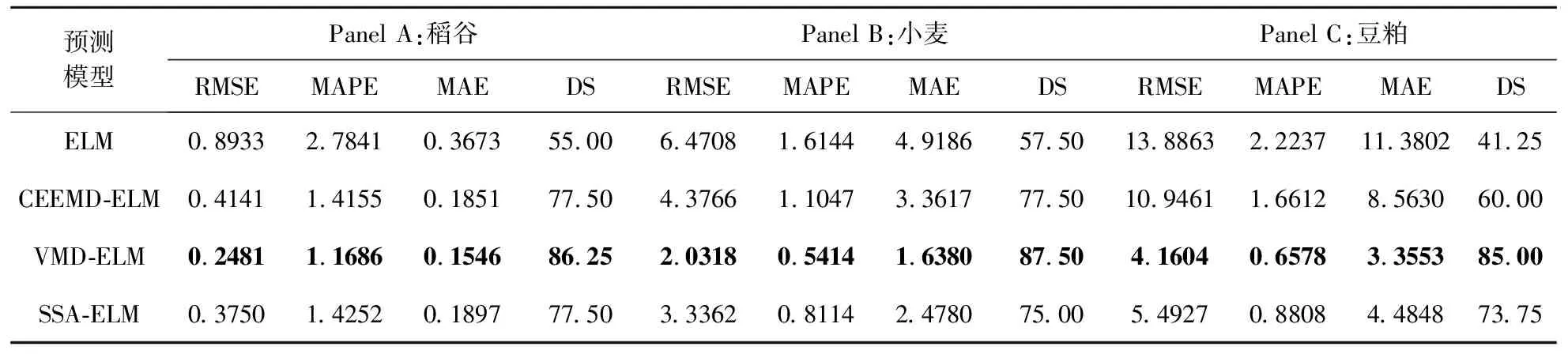
表1 预测模型预测精度

对比单预测模型和分解集成预测模型，所有分解集成预测模型的三种误差指标和方向性指标均优于单模型，这说明了分解集成策略的有效性。其中，所提出的VMD-ELM分解集成预测模型的小麦和豆粕期货预测的MAPE误差仅为0.6578%，0.5414%，对比单模型误差下降率为66.5%，70.4%。对比其他分解集成模型，VMD- ELM分解集成模型能够更好的将复杂的农产品期货数据分解为相对简单的子序列，减低单模型的预测压力，从而提升自身泛化能力，具有最优的预测性能。

3.4.2 VMD分解K值优化效果的比较分析

为验证所提出基于最小化模糊熵准则的K值优化法对VMD分解性能提升的有效性，统计并且比较分析VMD-ELM(1)、VMD-ELM(2)、以及所提出VMD-ELM的预测结果，获得的预测误差如表2所示，黑色加粗表示最优误差值。

表2 不同VMD分解K值优化方法预测误差

对比三种VMD分解模态K值选取方法，所提出的基于最小模糊熵准则的K值优化法的三种误差指标和方向性指标均优于其他两种。这有力的证明了基于最小模糊熵准则的K值优化法可以提高VMD的分解能力，使得预测模型能够更好的捕获时间序列的特征，从而提高预测精度。

3.4.3 统计学检验

为了更好的从数值上表示其中的差异，表3给出了所提出的模型与其他模型的统计学Diebold-Mariano(DM)检测P值结果。

表3 DM检测P值

从表3的DM检验结果可以看出，针对小麦、豆粕期货价格，DM检验的P值绝大部分都小于0.01，这说明在1%的显著性水平上，DM检验的结果拒绝两个模型的预测误差无显著性差异的零假设。也就是说，VMD-ELM在显著性水平为1%的情况下优于单模型，其他分解集成模型，和其他VMD分解K值优化方法。针对稻谷期货，DM检验的P值绝大部分都小于0.1，这说明所提出的VMD-ELM在显著性水平为10%的情况下优于单模型，其他分解集成模型，和其他VMD分解K值优化方法。这个结果从统计上证实了所提出的VMD-ELM分解集成预测模型的优越性。

4 结论

由于农产品期货市场价格具有高度复杂性，单一预测模型难以捕捉其规律特征。因此本文构建了VMD-ELM农产品期货价格分解集成预测模型，并且针对VMD分解关键参数模态数K值选择难题，提出了基于最小模糊熵准则的K值优化法，通过对CBOT交易所的稻谷、小麦和豆粕期货价格的实证研究，可以得出以下四个结论：(1)对比单预测模型和分解集成预测模型，所有分解集成预测模型的水平精度指标和方向性指标均优于单预测模型，这证实了分解集成策略在农产品期货价格预测的有效性。(2)对比3个分解集成预测模型，VMD-ELM的预测误差远远小于其他分解集成预测模型，这证实了VMD-ELM相比于其他的分解集成模型能够更好的将复杂的农产品市场期货价格序列分解为简单的子序列，减低单模型的预测压力，以此提高自身泛化能力，能有效的提高预测性能。(3)对比3种VMD分解K值选取方法，所提出了基于最小化模糊熵准则的K值优化法表现最佳，这证实了所提出的方法能有效避免VMD分解不足或过分解，从而提升模型的预测性能。(4)通过DM检验，在统计上证实了所提出VMD-ELM分解集成模型相比于其他模型具有更优的预测性能、更高的预测精度。