柔性作业车间调度与视情维修的联合决策
2023-03-02吴燕汝张晓红
甘 婕, 王 磊, 吴燕汝, 张晓红
(1.太原科技大学 经济与管理学院 工业与系统工程研究所,山西 太原 030024; 2.山西人文社科重点研究基地:装备制造业创新发展研究中心,山西 太原 030024)
0 引言
在制造企业中,生产调度和维修活动常发生冲突[1]。提前预防性维修(PM)能确保生产顺利进行[2]。但过多的预防性维修会影响正常的生产活动和企业效益[3]。因此,将生产调度与预防性维修活动相结合,解决两者间的冲突问题成为了制造领域的研究焦点。
柔性作业车间调度(FJSS)在传统调度的基础上,进一步考虑每道工序在不同设备选择加工的问题[4]。针对FJSS与PM的联合研究,E.Moradi等学者建立了相关决策模型,并结合理性策略与定周期策略进行维修决策[5]。路光明等分析了FJSS的鲁棒性,建立了两者的多目标联合决策模型[6]。刘永等研究联合决策模型时,考虑了设备的役龄约束[7]。杜阳宇等在此基础上,引入了可靠性控制因子,通过设备可靠性对维修活动进行决策[8]。Mirahmadi等针对同样的联合决策问题,提出了一个随机数学模型,该模型同时考虑到了最小化完工时间和最小化能源消耗两个方面[9]。
以上的决策研究中,采用多是基于时间的维修(TBM)策略。然而,随着传感技术的日益发展,设备状态可直接或间接检测获得,以致基于状态的预防性维修策略受到了广泛关注[10。采用视情维修策略(CBM),使得设备发生故障之前得到有效的预防维修[11。文献[12进行了综述,认为CBM策略较TBM策略更现实、更经济,决策时在TBM中,插入了适当的CBM。文献[13进行单机调度与CBM的集成研究,并建立了相应的优化模型。Fei等同时考虑了生产成本与完工时间两个目标,研究了基于可靠性的PM与流水车间调度的联合优化问题[14。文献[15]在FJSS和PM集成问题研究中,采用了TBM和CBM相结合的维修策略。
本文针对柔性作业生产车间,且劣化状态可直接或间接检测的设备,以FJSS调度序列和每项工序前进行CBM的逻辑变量作为决策变量,进行FJSS与CBM的联合决策研究。
1 问题描述
FJSS与CBM的联合决策包括以下问题:
(1)工序分配问题,将工序分配到可加工的相应设备;
(2)工序排序问题,各设备上的工序排序;
(3)维修决策问题,根据设备状态安排PM。
在FJSS与CBM的联合决策研究中,考虑以下假设:
(1)设备初始状态全新,加工作业在零时开始加工;
(2)忽略设备的初始设置和作业在不同设备间的移动时间;
(3)调度序列中每个位置只能加工一项作业,每项作业只能被分配到序列的一个位置上;
(4)工序的加工不可续;
(5)维修后,设备状态恢复全新;
(6)维修时,相应设备停工。
2 FJSS与CBM联合决策模型
2.1 符号定义
n:待加工作业总数;m:加工设备总数;
oi:待加工作业i的工序总数,i=1,2,…,n;
tijk:作业i的工序j在设备k上加工的时间,i=1,2,…,n,j=1,2,…,oi,k=1,2,…,m;
rk:设备k上被分配的加工作业总数;
D[r]k:设备k上第r项作业完工时,设备的劣化值,k=1,2,…,m,r=1,2,…,rk;
tP:预防性维修所需时间;tF:故障后更换所需时间;
ck:设备k上加工作业的完成时间。
决策变量符号定义如下:
xijk:FJSS的决策变量,在设备k上加工作业i的工序j;
yrij:FJSS的决策变量,在设备的第r个位置上,加工作业i的工序j;
z[r]k:维修策略的决策变量,判断设备k上第r项作业加工前设备是否被维修。
2.2 FJSS与CBM的联合策略
xijk确定了对作业i的工序j加工的设备,表达如式(1)所示:
(1)

(2)
维修策略的决策变量为z[r]k,表达为式(3):
(3)
联合策略:
1)当z[r]k=1时,进行维修活动,若D[r]k≥Dk,则安排故障更换;否则,安排预防性维修。
2)当z[r]k=0时,安排下一项加工作业,设备状态继续劣化。
2.3 模型建立
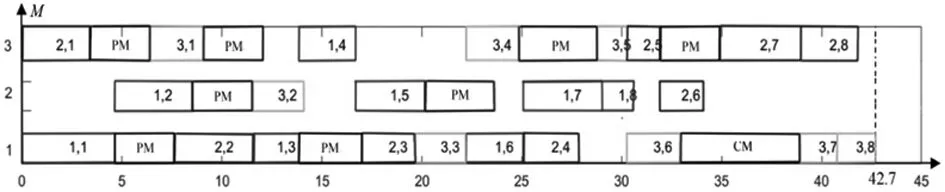
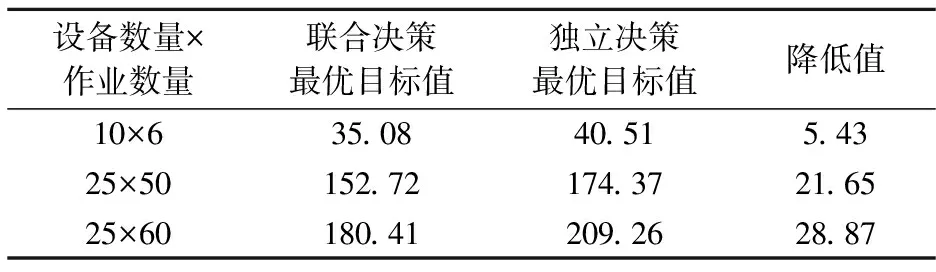
若D[r]k (4) 若D[r]k≥DF时,则进行故障后更换,维修概率表达如式(5): (5) 首先,对每项作业的第一道工序进行加工,j=1时,存在两种可能: 1)若该作业是设备k的第1项加工作业,r=1,则其作业的完成时间为:c[1]k=t[1]k。 2)否则,当前设备已有加工作业工序被加工,必须在加工完成当前作业工序后加工,即r>1,该作业的完成时间为: c[r]k=c[r-1]k+z[r]k(PP[r]k·tp+PF[r]k·tF)+t[r]k (6) 其次,按照既定的工艺流程,安排每项作业的其余工序,即j>1时,存在两种可能: 1)该作业是设备的第1项加工作业,r=1,则c[r]k=c[h]l+t[r]k,h≠l。 2)当前设备已有其它作业的工序被加工,必须在完成当前作业的工序后加工,即r>1,该作业工序的完成时间为: c[r]k=max{c[h]l,c[r-1]k+z[r]k(PP[r]k· tP+PF[r]k·tF)+t[r]k} (7) 以最大期望完工时间最小为优化目标,建立相应数学模型: (8) (12) 式(8)为目标函数; 式(9)与式(10)为FJSS的加工约束; 式(11)为预防性维修的决策变量; 式(12)表示只能在第k个设备的空闲期间安排维修。设备k上第r项作业开始时间(c[r]k-t[r]k),必须大于等于第r-1项作业的完成时间c[r-1]k与维修时间z[r]k(PP[r]k·tP+PF[r]k·PF[r]k·tF)之和。 假设设备在单位时间内的劣化增量ΔD~F(D),初始劣化为D[0]k=0。 选取第1台设备进行分析,当r=1时,设备运行第t[1]1个时间单位后完成第1项加工作业,此时设备的劣化状态由0增长为D[1]1,其概率密度函数表示为式(13): φ1=(D[1]1)=f(t[1]1)(D[1]1) (13) 当r=2时,劣化状态为D[2]1,加工时间为t[2]1。具体分析如下。 1)若z[2]1=0,设备未维修,概率密度函数为φ1=(D[2]1)=f(t[2]1)(D[2]1-D[1]1)。 2)若z[2]1=1,安排预防性维修,设备状态恢复全新,φ1=(D[2]1)=f(t[2]1)(D[2]1)。 根据前两式,φ1=(D[2]1)的计算公式为式(14): φ1=(D[2]1)=f(t[2]1)(D[2]1-(1-z[2]1)D[1]1) (14) 以此类推,第k台设备上,第r项作业完成后,D[r]k对应的概率密度函数通式为式(15): φk(D[r]k)=f(t[r]k)(D[r]k-(1-z[r]k)D[r-1]k) (15) 设t[r]k~U(1,5);ΔD~Γ(α,β),β=0.25,α1=4,α2=4.5,α3=5;tP=3,tF=6。3个工件分配到3台设备加工,每个工件有8道工序,每道工序对应2台设备。 加工数据如表1所示。 表1 可加工工序对应设备及加工时间 遗传算法参数:种群大小40,最大遗传代数500,交叉概率0.8,变异概率0.1,代沟0.8。 3.1.1 染色体编码设计 3.1.2 遗传算子设计 1)选择:采用轮盘赌的选择方法。 2)交叉:满足交叉概率,分别对工序调度序列和维修决策部分进行单点交叉操作。交叉后,调整新的染色体,以满足待加工工序对应设备的调度约束。 3)变异:满足变异概率,取[1,m]内的随机整数,替换调度序列中需变异的值,并调整工序以满足调度约束;再将维修决策部分的变异编码进行0/1变异。 图1 染色体编码示例 分别采用柔性作业车间调度与视情维修的联合决策和独立决策得到目标值,并进行比较分析。图2为根据表1给出的加工数据,由联合决策模型进行优化后所得的甘特图。 图2 联合决策结果的甘特图 如图2所示,柔性作业车间调度与视情维修联合决策中,最优目标值为36.11。同时调整调度序列与维修序列,以防止设备故障产生长时间停机维修。 两者独立决策。先在FJSS规则下,得到最大完工时间最小的调度序列;而后在该序列中插入维修,得到最优值为42.7,如图3。 图3 独立决策结果的甘特图 比较两种决策,联合决策比独立决策的目标值降低了6.59。在加工作业过程中,联合决策有利于减少调度决策和维修决策之间的矛盾。因此,联合决策可以获得更优的目标值。 为证明联合决策模型在不同加工作业规模下的有效性,随机生成了10×6、25×50和25×60不同规模,将联合决策与独立决策进行对比。如表2所示。 表2 不同加工规模下的优化结果 经比较,10×6规模下,联合决策的最优目标值相较于独立决策降低了5.43。25×50规模下,联合决策的最优目标值相较于独立决策降低了21.65。25×60大规模下,联合决策的最优目标值相较于独立决策降低了28.87。 结果表明,柔性作业车间调度和视情维修的联合决策相较于独立决策的最优目标值低,而且在加工规模越大的情况下,降低越多。 为判断所建模型的适用性及灵敏度,对联合决策的劣化参数α和tP/tD进行分析。 其余参数确定不变,对不同设备下不同α的情况分析相应目标值。 实验2中3台设备劣化参数取值为5,6,7,而实验1中的劣化参数取值为2,3,4,表明实验2中3台设备的劣化速度总体比实验1中3台设备的劣化要快。 表3 α对优化结果的影响 观察表3中α对优化结果的影响,随着α的增大,设备劣化速度加快,为了保证设备能正常运行,需要安排更多的预防性维修,致使目标最大期望完工时间增大,根据模型优化求解后,目标值E(cn)由37.62增加到44.89,且实验2中被安排了8次维修,而实验1中安排了5次预防性维修,实验2比实验1多安排了3次维修活动。 以M1,M2,M3为例,将tP/tF对优化结果的影响进行比较,分别取三个设备的劣化参数为α=2,3,4,如表4所示,其中PM为预防性维修次数,CM为故障更换次数。 表4 tP/tF对优化结果的影响 当tP/tF=1/6时,最大期望完工时间为32.23。联合决策中,安排了8次PM。柔性作业车间调度中,安排加工作业时,优先选择在加工时间较短的设备上进行加工。 当tP/tF=3/6时,目标值增加到37.62。进行了2次CM与5次PM。调度序列自适应调整,将部分作业安排到劣化速度慢的设备上加工,以得到最优目标值。 当tP/tF=5/6时,tP和tF接近,最大期望完工时间为40.61,进行了3次CM与5次PM。调度和维修序列同样依据联合决策结果进行调整,以得到最优目标值。 综上所述,模型对设备的劣化速度与预防性维修时间和故障后更换时间的比值都具有良好的敏感度。 针对可直接或间接检测获取劣化状态的设备,研究FJSS与CBM的联合决策问题。以FJSS的调度序列与CBM序列为决策变量,构建了最大期望完工时间最小的联合优化模型。推导了联合决策过程中相应的概率密度函数。通过联合决策与独立决策的数值分析结果对比和对劣化参数的敏感度分析,验证了本文所建模型的有效性。基于此研究思路,可以对柔性作业车间调度与非完美视情维修的联合决策进行进一步研究。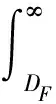

2.4 概率密度函数
3 数值分析
3.1 模型求解


3.2 联合决策优化模型验证

3.3 灵敏度分析


4 总结与期望
