具有图结构和联盟结构的Banzhaf值及应用
2023-03-02单而芳刘贺宇吕文蓉史纪磊
单而芳, 刘贺宇, 吕文蓉, 史纪磊
(上海大学 管理学院,上海 200444)
0 引言
可转移效用合作对策(cooperative game with transferable utility)[1],简称TU-对策,描述的是参与者间通过形成合作联盟,产生一定的联盟效用。该模型假设任何有限参与者间都可能形成合作联盟(coalition for cooperation),即任何联盟都是可行的。针对TU-对策,Shapley[2]以每个参与者为分析对象, 对参与者合作产生的联盟效用提出了一种分配规则,即Shapley值。TU-对策中另一个著名分配规则是由Owen[3]提出的Banzhaf值,该值起源于投票对策,后被逐步拓展到TU-对策中。Shapley值和Banzhaf值都是通过参与者的边际贡献来度量的,可以看作参与者对所有联盟产生的边际贡献的期望值。不过,它们对于每个联盟边际贡献的权重定义是不同的。具体地,在Shapley值中,规定每个参与者加入任何相同规模联盟的可能性是相同的,而在Banzhaf值中,规定参与者加入任何联盟的可能性都是相同的。对于总效用的分配,Banzhaf值的计算方式比Shapley值更为简单。
实际中,并非所有参与者间均能进行有效合作。为描述该合作约束,Myerson[4]引入图(graph)的概念,将TU-对策和图结构结合,提出了具有图结构的TU-对策,简称图对策(graph game)。图中的节点(node)代表参与者,图中的边(link)代表参与者之间存在的某种合作关系,且假设只有在有边或路(path)连通的情况下,参与者间才能形成合作联盟。在此基础上,定义图限制对策(graph-restricted game)上的Shapley值作为图对策中的一种分配规则,即著名的Myerson值。同样使用图结构描述参与者间的合作约束。Owen[5]对Banzhaf值进行了研究,提出了图限制对策中的Banzhaf值,简称为Banzhaf图值(Banzhaf graph value)。之后,Alonso-Meijide和Fiestras-Janeri[6]给出了Banzhaf图值的四种公理性刻画。第一种是使用独立性(isolation)、二合并性(pairwise merging)和公平性(fairness);第二种是利用分支总贡献性(component total power)和公平性(fairness);第三种和第四种由平衡贡献性(balanced contributions)代替公平性得到。其他以图结构描述合作约束的研究可参见[7~11]。
不同于Myerson[4]用图结构描述参与者间的合作约束,Owen[12]使用联盟结构描述合作约束,分析优先联盟(priori union)对效用分配造成的影响,提出了具有联盟结构的TU-对策(TU-games with coalition structures),并定义了具有联盟结构的Banzhaf值(简称Banzhaf-Owen值)作为该对策上的一种分配规则。考虑对称性,Alonso-Meijide和Fiestras-Janerio[13]提出了具有联盟结构的Banzhaf值的另一种修正形式,即对称联盟Banzhaf值(symmetric coalitional Banzhaf value)。类似的,Kamijo[14]定义了联盟结构TU-对策上的分割限制对策,提出并刻画了该结构下的一种新的分配方案,即Ka值。Owen值和Ka值所定义的联盟结构的不同点在于前者的优先联盟中的部分参与者可以和其他完整的优先联盟进行合作,而后者则假定只有完整的优先联盟间才能进行完全合作。
合作的复杂性使得合作往往受两种甚至多种形式的约束。Alonso-Meijide等[15]考虑了具有联盟结构和图结构双重限制的TU-对策,将Banzhaf-Owen值和对称联盟Banzhaf值推广到了该模型中。而van den Brink等[16]则将Ka值和Myerson值推广到具有联盟结构和图结构的TU-对策(TU-games with coalition and graph structure)上,提出了图-分割值(graph-partition value)和分割-图值(partition-graph value),即具有图结构的Ka值和具有联盟结构的Myerson值,并进行了公理性刻画。这两个值都是Shapley值的推广,而Banzhaf值在该形式下的推广尚未有学者进行研究。
本文旨在将Banzhaf值推广到具有联盟结构和图结构的TU-对策上,提出并刻画一种新的具有联盟结构和图结构的Banzhaf值。本文结构安排如下: 第二节给出本文需要的基本定义和符号。第三节给出具有联盟结构和图结构的Banzhaf值的定义,并进行公理性刻画。第四节以天然气管道案例进行分析,将具有联盟结构和图结构的Banzhaf值与其他值进行比较分析。最后对本文所做工作进行总结并给出注记。
1 预备知识
1.1 TU-对策
可转移效用合作对策,简称TU-对策,是由二元组(N,v)组成。其中N表示有限参与者(player)集,v表示特征函数(characteristic function),它是定义在2N→R上的一个映射,并规定v(Ø)=0。对N中任意一个非空子集S,v(S)表示联盟中成员进行合作所产生的效用,用s表示联盟S的基数。(S,v|S)是(N,v)的子对策,且对任意的T⊆S,有v|S(T)=v(T)。为了简便,我们将v({i,j,…,k})简记为v(i,j,…,k),相应的也将S∪{i}简记为S∪i。
支付向量(payoff vector)x=(x1,x2,…,xn)∈Rn是指分配给每个参与者i的支付为xi。TU-对策的一个分配规则(allocation)或者值是一个函数f,指分配给任意(N,v)的一个支付向量f(N,v)∈Rn。对于TU-对策(N,v)和任意的i∈N,Shapley值Sh(N,v)[2]是TU-对策上最著名的一个分配规则,其定义为:
TU-对策中,另一个分配规则是Banzhaf值[3],其定义如下:
(1)
1.2 图和通讯情境
图(graph)由有限点集N和无向边集L⊆LN={{i,j}|i,j∈N,i≠j}组成,用二元组(N,L)表示,其中LN称为N上的完全图。在参与者集合N固定时,我们将(N,L)简记为L。记所有的图(N,L)的集合为LN。为简便起见,文中将{i,j}简记为ij。
如果对任意k=1,2,…,p-1,都有ikik+1∈L,则称点集(i1,i2,…,ip)为L中的一条路。如果i和j间存在一条路或者i=j,则称i和j在L中是连通的。如果图L中任意两点间均是连通的,则称图L是连通的。对于任意的S⊆N,图(S,L(S))称为L在S上的子图,其中L(S)={{i,j}∈L|i,j∈S}。对于任意的S⊆N,如果S中任意两点在L(S)上均是连通的,则称S在L上是连通的。一个极大的连通子集S称为L上的一个分支。将(S,L(S))和(N,L)中所有分支的集合分别记为S/L和N/L。用(N,L-ij)表示由(N,L)去掉边ij后形成的图,用Li={ij∈L|j∈N}表示L中所有与i相关的无向边的集合,记L-i,LLi表示去掉所有与i相关的无向边后形成的子图。
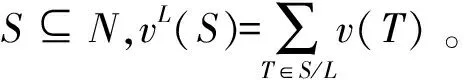
1.3 具有联盟结构的TU-对策
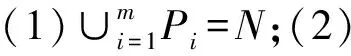


2 具有联盟结构和图结构的Banzhaf值及其公理化刻画
2.1 具有联盟结构和图结构的Banzhaf值
具有联盟结构和图结构的TU-对策由四元组(N,v,L,P)组成,其中(N,v)代表TU-对策,(N,L)代表图,而(N,P)代表联盟结构。记所有具有联盟结构和图结构的TU-对策(N,v,L,P)的集合为PN。对任意的(N,v,L,P)∈PN,van den Brink等[16]将分割-图限制对策(N,(v|P)L)的特征函数定义为:对任意的S⊆N
(2)
在上述理论基础上,本文将Banzhaf值拓展到具有联盟结构和图结构的TU-对策中,定义一种新的具有联盟结构和图结构的Banzhaf值,简称为PL-Banzhaf值。
定义1(PL-Banzhaf值) 对于任意的(N,v,L,P)∈PN,PL-Banzhaf值Ψ(N,v,L,P)可定义如下:对任意的i∈N
Ψi(N,v,L,P)=ξi(N,v1P,L)=Bai(N,(v|P)L)
(3)
显然,当P为平凡联盟,也即P={N}或P={{1},{2},…,{n}}时,PL-Banzhaf值就是Banzhaf图值。进一步,当P为平凡联盟并且图是完全图时,PL-Banzhaf值就是Banzhaf值。因此,PL-Banzhaf值是Banzhaf图值和Banzhaf值的一类自然推广。
2.2 PL-Banzhaf值的公理化刻画
本节将给出PL-Banzhaf值的公理性刻画。为方便刻画,我们首先介绍一些性质。

分割分支总贡献性是指:分支的总效用等于该分支内每个参与者限制在该分支子对策上的效应之和。
公平性(Fairness,简记为FA)。对任意(N,v,L,P)∈PN,及任意的ij∈L,i,j∈N,若分配规则f∈Rn满足fi(N,v,L,P)-fi(N,v,L-ij,P)=fj(N,v,L,P)-fj(N,v,L-ij,P),则称f具有公平性。
公平性是指:与一条无向边关联的两个参与者,当去掉这条无向边时,对这两个参与者支付造成的影响是相同的。
引理1对任意的(N,v,L,P)∈PN,PL-Banzhaf值Ψ(N,v,L,P)满足FA。
证明由定义1及Banzhaf图值满足FA[6]易得:
Ψi(N,v,L,P)-Ψi(N,v,L-ij,P)
=ξi(N,v|P,L)-ξi(N,v|P,L-ij)
=ξj(N,v|P,L)-ξj(N,v|P,L-ij)
=Ψj(N,v,L,P)-Ψj(N,v,L-ij,P)
所以Ψ(N,v,L,P)满足公平性,引理得证。
平衡贡献性(Balanced contributions,简记为BC)。对任意(N,v,L,P)∈PN及i,j∈N,若分配规则∈Rn满足fi(N,v,L,P)-fi(N,v,L-j,P)=fj(N,v,L,P)-fj(N,v,L-i,P),则称f具有平衡贡献性。
平衡贡献性是指:i和j为联盟N中的两个参与者,参与者i选择孤立自己对参与者j支付的影响与参与者j选择孤立自己对参与者i支付的影响是相等的。
引理2对任意的(N,v,L,P)∈PN,PL-Banzhaf值Ψ(N,v,L,P)满足平衡贡献性(BC)。
证明由定义1及Banzhaf图值满足BC[6]易得:
Ψi(N,v,L,P)-Ψi(N,v,L-j,P)
=ξi(N,v|P,L)-ξi(N,v|P,L-j)
=Ψj(N,v,L,P)-Ψj(N,v,L-i,P)
所以Ψ(N,v,L,P)满足平衡贡献性,引理得证。
定理3对任意的(N,v,L,P)∈PN,PL-Banzhaf值Ψ(N,v,L,P)可由公平性(FA)和分割分支总贡献性(PCTP)所唯一确定。
证明存在性。对于任意(N,v,L,P)∈PN,根据引理2可知,PL-Banzhaf值Ψ(N,v,L,P)满足公平性。而由Banzhaf图值满足分支总贡献性易证PL-Banzhaf值满足PCTP。
唯一性。假设存在另一个满足FA和PCTP的分配规则f,我们需证明f=Ψ。当|L|=0时,即L为空图。此时,每个节点i∈N都是一个分支,由PCTP可得:fi(N,v,Ø,P)=v(i)=Ψi(N,v,Ø,P)。
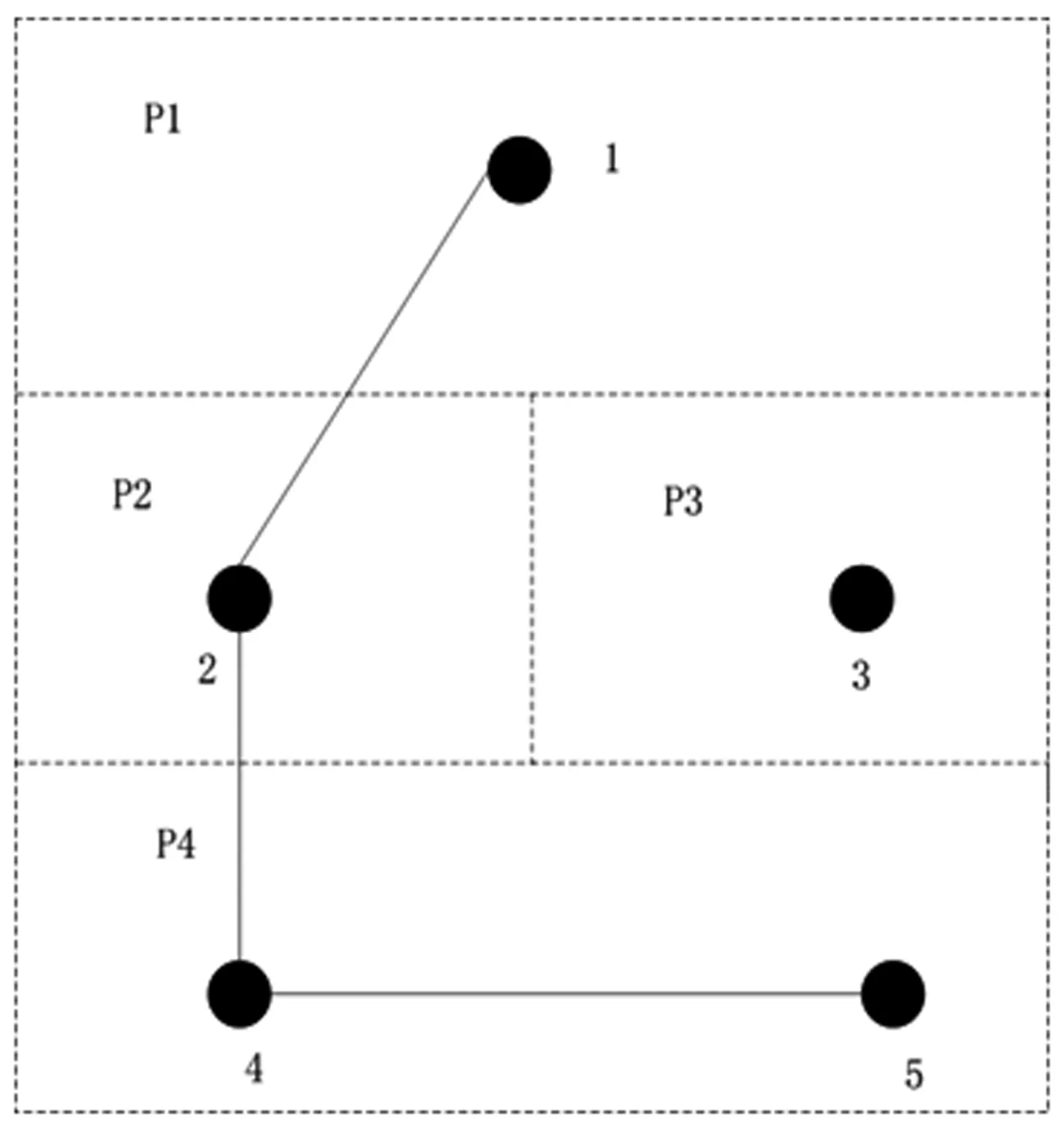
现假设对任意的(N,v,L,P)∈PN,i∈N,当|L| fi(N,v,L,P)-fj(N,v,L,P) =fi(N,v,L-ij,P)-fj(N,v,L-ij,P) =Ψi(N,v,L-ij,P)-Ψj(N,v,L-ij,P) =Ψi(N,v,L,P)-Ψj(N,v,L,P) 即,fi(N,v,L,P)-Ψi(N,v,L,P)=fj(N,v,L,P)-Ψj(N,v,L,P)。 根据分支内参与者间的传递性可知,存在一个实数d,使得对任意i∈S∈S/L,有fi(N,v,L,P)-Ψi(N,v,L,P)=d。进一步结合PCTP可得: 因为s≠0,所以d=0,即fi(N,v,L,P)=Ψi(N,v,L,P)。 综上所述,对任意的i∈N,均有fi(N,v,L,P)=Ψi(N,v,L,P),定理得证。 引理4对任意的(N,v,L,P)∈PN,PL-Banzhaf值Ψ(N,v,L,P)满足平衡贡献性(BC)必定满足公平性(FA)。 证明对于对策(N,v,L,P)及任意的i,j∈N,由PL-Banzhaf图值满足BC可知: Ψi(N,v,L,P)-Ψi(N,v,L-j,P) =Ψj(N,v,L,P)-Ψj(N,v,L-i,P) (4) 对任意的i,j∈N及对策(N,v,L-ij,P),由PL-Banzhaf图值满足BC可知: Ψi(N,v,L-ij,P)-Ψi(N,v,(L-ij)-j,P) =Ψj(N,v,L-ji,P)-Ψi(N,v,(L-ij)-i,P) (5) 容易验证(L-ij)-j=L-j及(L-ij)-i=L-i成立。进一步,式(5)可化简为 Ψi(N,v,L-ij,P)-Ψi(N,v,L-j,P) =Ψj(N,v,L-ij,P)-Ψj(N,v,L-i,P) (6) 将式(4)和式(5)相减可得 Ψi(N,v,L,P)-Ψi(N,v,L-ij,P) =Ψj(N,v,L,P)-Ψj(N,v,L-ij,P) 所以Ψ(N,v,L,P)满足BC必定满足FA,引理得证。 结合引理2、引理4和定理3可得关于PL-Banzhaf值的新刻画。 定理5对任意的(N,v,L,P)∈PN,PL-Banzhaf值Ψ(N,v,L,P)可由平衡贡献性(BC)和分割分支总贡献性(PCTP)所唯一确定。 跨国运输问题一般均可抽象为具有联盟结构和图结构的TU-对策,其中每个国家代表一种联盟结构,天然气运输管道代表图结构。本节将引入一个跨国天然气管道运输案例,分析PL-Banzhaf值的合理性和优势。 图1 跨国天然气管道运输模型示意图 考虑由五个地区构成的天然气跨国运输模型。N={1,2,3,4,5}是地区集合,其中地区1坐落在P1国,地区2坐落在P2国,地区3坐落在P3国,地区4和地区5属于同一个国家,记为P4国。地区1是天然气的主要出口区,通过现有的天然气管道将天然气运送给其他各区。而地区3是天然气自给自足区,产生的天然气仅供给本区使用,且不需要进口。将国家抽象为联盟结构,天然气管道抽象为图结构,可将上述模型抽象为如图1所示的结构。其中边集L={12,24,45},联盟分割为P={P1,P2,P3,P4}={{1},{2},{3},{4,5}} 根据上述假设可知,地区3自身即可产生收益,不需与其他地区合作。地区1自身可以产生收益,也可通过与其他地区合作获得更大的收益。而其他地区均需包含天然气的出口区1时才会产生收益。现只考虑每个地区在运输过程中产生的效用,据此,我们定义如下特征函数: 根据式(1)、式(2)和定义1,计算可得各地区的PL-Banzhaf值Ψ如表1所示,表中同样还列出了Banzhaf值Φ、Banzhaf图值Π、Banzhaf-Owen图值[12]ξ和λ[13]。 表1 跨国天然气管道运输案例各值计算结果 分析表1可知,Banzhaf值没有考虑到各地区间所属的国别差异和天然气管道的限制,给予了地区2最低的分配值。但实际上,地区1往地区4和地区5运输天然气时必须经过地区2,因此,Banzhaf值并未体现出地区2在天然气运输过程中的作为必要枢纽的重要性。Banzhaf图值虽然体现出了地区2作为必要枢纽的重要性,但未考虑到联盟结构。Banzhaf-Owen值和对称联盟Banzhaf值虽然同时考虑了图结构和联盟结构,但并未体现联盟结构内合作共赢的理念。一般而言,选择天然气进口区时会倾向于选择能使国家内所有需求区都能获得最大效用的地区,因此需征求所有地区的意见,而Banzhaf-Owen值和对称联盟Banzhaf值使用的联盟结构定义并不满足该条件。本文提出的PL-Banzhaf值,则能够很好适应该结构。 注意到PL-Banzhaf值不满足有效性,因此这个值不一定在核心中。 本文给出了一种新的具有联盟结构和图结构的Banzhaf值(PL-Banzhaf值)的定义及其满足的性质,它是对Banzhaf值的一类推广。首先,通过公平性、平衡贡献性和分割分支总贡献性,给出了PL-Banzhaf值的两种刻画方式。其次,根据跨国天然气管道运输案例分析,PL-Banzhaf值相比其他分配规则更能提出参与者在运输过程中以及联盟协商中的地位。另外,van den Brink等[16]指出联盟结构和图结构考虑的先后顺序不同时,会形成两种不同的限制对策,本文只考虑了其中一种,而另外一种也是十分具有研究意义的。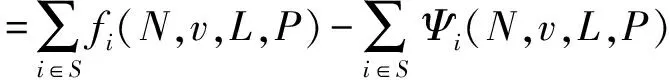
3 应用举例—天然气管道运输问题


4 结论及注记
