辨析问题结构 提升解题效率 追求德育价值
2023-03-02何承生
何承生
(浙江师范大学附属中学,浙江 金华 321004)
高考试题、强基试题等往往有比较深广的数学背景,有些试题思路宽广、灵活又有趣味,能考查学生的优秀思维品质和逻辑推理能力.笔者对一些高考试题和强基试题进行分析后,结合问题的结构特征做出进一步的探索,寻找妙解之道.如此也更有利于激发学生的学习兴趣,从解题教学维度渗透数学的德育价值.
1 结构决定思路
先以一道高考题为例,说明抓住问题“结构”特征的重要性.


2)略.
(2022年全国数学新高考Ⅰ卷第18题)

视角2(分式结构)条件为分式结构,可能会想到十字相乘法,处理思路为:由已知条件得
sin 2B+sinAsin 2B=cosA+cosAcos 2B,
整理得 sin 2B=cosA+cosAcos 2B-sinAsin 2B,
即
sin 2B=cosA+cos(A+2B).
化成上述等式是基于角的特点,等式右边利用和差化积公式化简得到的结构更美观、更简洁,想到和差化积则是因为等式左边为积(sin 2B=2sinBcosB)的结构.而
cosA+cos(A+2B)=-2cosBcosC,
从而
2sinBcosB=-2cosBcosC,
即
(sinB+cosC)cosB=0,
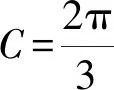
视角3(倍角结构)等式左边为单倍角A,右边为二倍角2B,可能会想到将等式右边的2B化为单倍角B,于是就产生如下思路:


(1)
根据式(1)的分式结构,我们会想到以下3种处理方法:
方法1(分式结构)将式(1)十字相乘化为
cosAcosB=(1+sinA)sinB,
重新组合后得 sinB=cos(A+B)=-cosC,
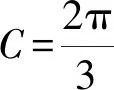
方法2(同名结构)式(1)左右两边都化为正切
得到
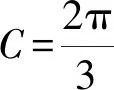
视角4(化边结构)例1条件中式子的左右两边均为关于“角”的关系,可能想到转化成“边”处理,但式(1)的结构不具备化边的条件,故不可行.
可将“角”化为“边”处理的结构如:
1)2022年全国数学高考乙卷理科第17题中条件“sinCsin(A-B)=sinBsin(C-A)”,此结构具备等式两边正弦“sin”齐次的特征.
2)2021年全国数学新高考Ⅰ卷第19题中条件“BDsin∠ABC=asinC”,此结构也具备等式两边正弦“sin”齐次的特征.
可能还有其他视角处理本题结构的方法,但无论从什么视角处理,都是基于对问题“结构”的理解,即结构决定思路.
2 结构决定思路的内因
数学经历几千年的积累与发展,逐步通过自身独特的符号、思维诠释世界,有图形的语言、数的语言,并通过数学符号、图像形状、函数方程等不同的结构展示世界的内涵.《普通高中数学课程标准(2017年版)》指出:数学是研究数量关系和空间形式的一门科学.数学源于对现实世界的抽象,基于抽象结构,通过符号运算、形式推理、模型构建等,理解和表达现实世界中事物的本质、关系和规律.美国著名数学教育家斯蒂恩曾说:“数学应被看成是一种结构性科学.”千变万化的现象背后都有内在的道理,而数学的功能,则是将现实世界的性质、定理、原理、规律等通过结构表达出来,因此结构是数学本质的一种体现.
下面笔者以“垂直”为例说明与垂直有关的数学结构.
在学生还未建立“垂直”概念前,生活中形形色色垂直的形象为他们理解“垂直”奠定了经验基础,该阶段学生对垂直结构的认知应是这些具体的形状.
在小学阶段,垂直的形象具体为“两条相交直线为直角”,垂直的结构可以是某某角为90°,用“⊥”符号表示,进一步发展为正方形、长方形、直角三角形等图形结构,该阶段垂直结构发展为符号语言和抽象形状.
在初中阶段,垂直的结构可以体现在:勾股定理、直径所对的圆周角等,该阶段垂直结构发展为代数方程和性质定理等.
在高中阶段,垂直的结构在立体几何、向量、解析几何中都有多种不同形式的体现,如在立体几何中,线面垂直、面面垂直、线面角、二面角大小等都有其对应的几何模型,这些几何模型中都含有与垂直有关的结构.另外,解析几何中也有大量与垂直有关的结论.
因此,不同的数学知识通过特定的文字、符号、图形展示世界的原理,不同的结构特征背后蕴涵着内在的数学知识,通过剖析数学问题的结构寻找解题思路是有依据的.
3 基于结构提升解题效率
笔者选取“比较大小”“倒根方程”两类问题,通过结构启发解题思路,以期提升解题效率.
3.1 比较大小问题

( )
A.a C.b (2021年天津市数学高考试题第5题) ( ) A.a C.c (2022年全国数学新高考Ⅰ卷第7题) ( ) A.c C.a (2022年全国数学高考甲卷理科试题第12题) 例5已知9m=10,a=10m-11,b=8m-9,则 ( ) A.a<0 C.b>a>0 D.b>0>a (2022年全国数学高考甲卷文科试题第12题) 思路可能会想到构造函数法,也可能将条件转化为9m=10,10m=a+11,8m=b+9,看到这3个式子左边的结构,可能会想到画出指数函数y=8x,y=9x,y=10x的图象.若m=1,则8m,9m,10m这3个数相差1,但实际m>1.根据指数函数的变化特点,8m,9m,10m这3个数差值大于1,从而8m<9m-1.由10m>9m+1,知b+9<9,又a+11>11,可选出答案. 2)若α是方程f(x)=0的根,则α+k是方程f(x-k)=0的根. ( ) D.前3个答案都不对 (2020年北京大学强基计划试题第4题) 思路针对问题中的分式结构,可能想到通分之类的处理办法,但通分后式子的结构较为复杂,化简较为烦琐,运算量大.我们还可依据以下结构特征尝试破解方法: 1)针对“已知……是方程……的4个复根”结构,可能会想到韦达定理; 因此,本题可以这样处理:由 记p(x)=x4+2x3+3x2+4x+5,则a+2,b+2,c+2,d+2是p(x-2)=0的4个根,展开得 p(x-2)=x4-6x3+15x2-16x+9=0. 其倒根方程为 1-6x+15x2-16x3+9x4=0, 从而 故选A. (2020年北京大学高水平艺术团招生文化课测试第1题) 之后便可求解问题,此思路是将根的通项公式表示出来,先分后合,方法自然清晰,对化简能力、运算能力要求较高.结合例6的经验,此题也具有类似的结构特征,故有以下思路: 思路2显然2,x1+1,x2+1,…,x2 018+1是方程(x-1)2 019-1=0的所有根,由二项展开得 (2021年北京大学优秀中学生暑假学堂数学测试第7题) 思路同例7,不再赘述. 解易知i+xj(其中j=1,2,…,2 021)是方程(x-i)2 021=1的根,展开得 (2) 其倒根方程为 (3) 从而 评注其实我们只需要方程(2)和方程(3)左端的最后两项,甚至从方程(2)就可以得到结果,例6和例7也是如此. 由此说明,问题的结构一定程度上决定了解题的思路,不同的结构也会启发不同的思考角度,造成不同解法之间效率的差别. 真正的教学是教人,而不是教书,学科教师不是教学科,而是用学科来教人[2],数学的育人功能应着眼于培养学生的逻辑思维能力、灵动思考能力.解题教学也是如此,不能只着眼于算出答案,不能为了解而解,让学生觉得数学就是做题目,通过大量刷题、重复训练以提升解题能力,这样会弱化数学的育人功能,不利于数学文化的传播,难以体现数学的教育价值.那么通过剖析结构寻找思路的解题教学蕴涵哪些教育价值呢?笔者浅说几点. 1)积累经验,巩固知识,提高解题效率.通过剖析问题的结构,是对所学知识的再认识,将已学知识进行联系和区别,方能从众多已有经验中调取与当前问题相关的经验迅速做出判断,寻找解决问题的最佳方法和路径,从而高效、正确地解决问题.这就要求教师在教授新知识时也需抓住知识的结构特征,深入剖析以引导学生清楚知识的结构体现,通过结构引领教学、练习,达到巩固数学知识、基本技能的目的,进而提升解题效率. 2)择题标准,注重思维,锻炼思考能力.教师选择例题和习题,依据应是重思维轻运算.如果一道题运算过分复杂,那么运算会掩盖思维的价值,影响思想方法的渗透,加重学习负担,让学生失去学习兴趣.尽管高考的压轴题运算量大,但与其所蕴涵的思维价值、处理结构的方法价值相比,运算地位是次要的,也不能说运算量大就不是好题.总之解题教学所选择的问题应更注重思维的价值,这应是好题的标准之一,也是落实“减负增效”的好办法.问题的结构是思维的载体,教师进行解题教学时,不妨精选一些结构特征比较明显的问题,以锻炼学生的思考能力. 3)数学结构,生活结构,提升数学素养.不仅数学知识有结构,其他学科知识有结构,生活中的问题也有着独特的结构.学习时依据不同的结构将知识进行分类,拿到一个问题,应思考:问题有什么特征、有什么结构、该怎么处理等,进而掌握解决问题的普适思想与方法,养成良好的数学思维习惯,从而提升数学素养.通过结构重塑对数学思想方法的认识,这些思想方法是知识迁移的基础,是应对变化的根本,是产生灵动思考的保障,有助于提高学生的学习力、思考力,对问题结构的处理能力潜移默化中转变为对生活中各式各样问题处理的能力,为未来的学习与生活所需提供更坚实的本领.

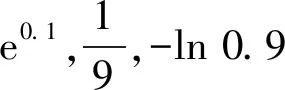
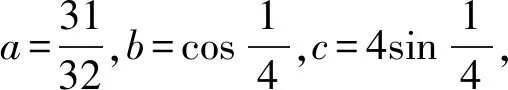
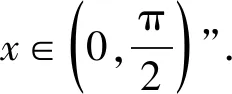
3.2 倒根方程问题





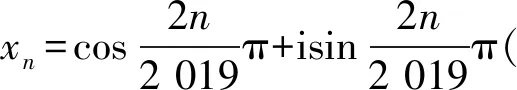


4 解题教学的德育价值
