深度学习理念下初中几何解题教学的策略研究
2023-03-02徐国安
徐国安
(银湖实验中学,浙江 杭州 311400)
所谓深度学习,指在真实复杂的情境中,学生运用所学的本学科知识和跨学科知识,运用常规思维和非常规思维,将所学的知识和技能用于解决实际问题,以发展学生的批判性思维、创新能力、合作精神和交往技能的认知策略[1].深度学习拥有如下3种特质:基于学科本质的真正革新的学习;主体性对话性的学习,即通过同伴的协作能够达到认知极限的课题学习;学习者自身能够体悟到学习深度的“深度学习”[2].
20世纪著名数学家傅种孙先生在《高中平面几何》的自序中说:“几何之务,不在知其然,而在知其所以然;不在知其然,而在知何由以知其所以然!”向着傅先生“几何之务”的目标和深度学习的3种特质,笔者在浙江省特级教师王红权名师工作室的导引下,结合深度学习理念对初中几何解题教学提出了以下几点策略.
1 重“想”轻“做”,思维可视,形成图式
在几何教学中,常听到教师讲“怎么做”,很少听到教师问“怎么想”,然而学生的思考肤浅无序,无法形成做几何题系统化、结构化的问题解决策略.以下是两个同课异构课的教学片段:

图1
片段1
例1已知AB是⊙O的直径,点C是⊙O上一点,联结BC,AC,过点C作CD⊥AB于点D,F是⊙O上的点,联结BF,与直线CD交于点G.求证:BC2=BG·BF.
师:分析后,“怎么做”这个题?如何找到等式BC2=BG·BF左右两边的联系?
生1:根据射影定理可得BC2=BD·BA,因此只需要证明BG·BF=BD·BA.
生(众):对的!接下来通过“相似”应该可以证明……
师:很好!根据射影定理,所证的结论实现了转化,转化为BG·BF=BD·BA后,如何证明呢?有同学说“可以用相似证明”,可以吗?等积式如何转化?
生3:好!我知道了!联结AF,利用“反A字”基本图形证明△BAF∽△BGD.
师:非常不错!根据刚才几位同学的回答,我们完成了这个例题的解答.让我们看下一题吧……
片段2
师:这个问题中,需要证明一组线段的“等积式”,同学们“怎么想”?

可见平时真是“训练有素”!这样的“顺口溜”真可谓是“一桥飞架南北,天堑变通途”.
师:这个想法非常好!但是这里行得通吗?含有平方关系的等积式,我们该“怎么想”?

图2
生1:勾股定理.
生2:射影定理.
生3:共边共角型,如图2.
师:这些想法都是不错的!我们再读题分析一下,看看从哪里切入?
生4:根据射影定理可得BC2=BD·BA,因此只需要证明BG·BF=BD·BA.
生5:对!再转化为等比式,然后找相似,但是相似……
师:好!既然直接找不到相似,那么我们再看看条件“AB是⊙O的直径”,该“怎么想”?
生6:遇直径想直角!联结AF,我知道怎么证了!
教师小结当我们看到“平方关系的等积式”,首先会想到“共边共角型相似”,其实射影定理也是特殊的“共边共角型相似”,同时联想能不能通过等线或等比来代替.结合题目条件,从图中“提取”几何基本图形,比如这个题中的“双垂型”和“遇直径想直角”的常用辅助线添法,找到已知和未知的联系.
片段1注重“怎么做”,片段2注重“怎么想”.笔者认为,几何解题教学中,按照“几何解题图式”,让学生经历“读题→上图(画图)→识图→可知”的循环审题过程打开思维,教师追问“怎么想”,重“想”轻“做”,启迪学生的思维,学生不断从已有的认知结构中检索“知识与方法”“图形与联系”,并充分暴露自己的思维,展现元认知的过程,通过系统化、结构化的理解,最终完成“怎么做”,才能真正形成深度的结构性思维.
2 单元视角,注重关联,形成结构
崔允漷教授指出,单元整体教学中的单元和教材中的单元是有区别的.这里所说的单元是一种学习单位,一个单元就是一个学习事件、一个完整的学习故事,因此一个单元就是一个微课程.一个学习单元由素养目标、课时、情境、任务、知识点等组成,单元就是将这些要素按某种需求和规范组织起来形成一个有结构的整体.
在几何教学中,我们从把握几何教学的整体结构入手,通过单元视角来组织教学,并注重教学中的知识关联、活动关联和方法关联,帮助学生理解知识的本质特征,让学生主动建构并形成认知结构.笔者在组织几何计算(单元)教学中进行了结构化的方法梳理,即几何计算包含求线段长度和求角度两大范畴,进而衍生出求面积、求比值、求三角函数值、求几何最值等.几何计算的整体思维框架如下:

结合这一思维框架,在几何计算教学中,笔者引导学生形成总的解决问题的思维框架:分析问题时先进行“内部分析”,即在一个三角形或一个四边形内部根据特殊三角形的性质,结合三角函数、面积法探寻解题思路,当思路“遇阻”,则寻求“外部力量”,探寻能否通过“全等”和“相似”来找到合适的解题路径.比如:在“求长度”教学中,让学生形成“勾股定理→三角函数→面积法→全等(相似)→坐标法→……”的解题结构路径.
在搭建解决问题的思维框架的同时,注重知识、方法的关联,以形成单元视角中的结构.比如在“求面积”教学中,教师可引导学生梳理具有层次性、递进性和关联性的模型结构(如图3):
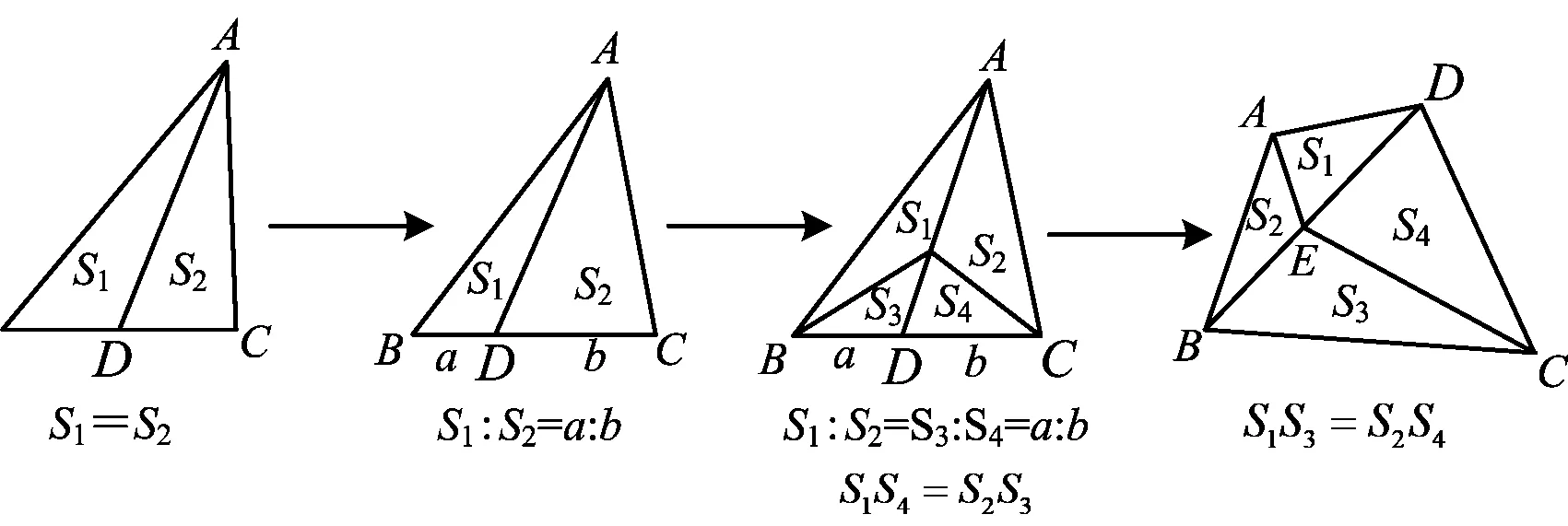
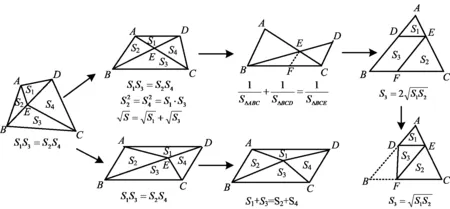
图3
在课堂上,教师组织学生经历这样的图形分析和比较的过程,引导学生学会关注共性,分辨差异,形成合适的“类”,借助图形分析问题,发展模型观念,从而激发学生的高阶思维,学会用数学的语言表达现实世界,提升学生的数学核心素养[3].
3 一题多变,关注逻辑,主线清晰
波利亚曾形象地说:“好问题同某种蘑菇有些相像,它们都成堆地生长,找到一个以后,你应当在周围找找,很可能附近就有好几个.”在几何教学中,教师要引导学生运用类比和联想,通过“因果逆向化、条件一般化、条件特殊化、结论一般化、结论开放化、图形拓展化”的变式手段,注意厘清变式中的知识主线或方法主线或基本图形主线,同时关注内在的逻辑关联,探索问题的发展变化,使其在更深入、更透彻地理解核心问题本质属性的同时拓展了数学思维,起到事半功倍的教学实效.
3.1 因果逆向化
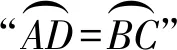

图4

3.2 一般化和特殊化
在几何变式教学中,通常能看到条件的特殊化或一般化,以及结论的一般化或特殊化.“一般化或特殊化”的变式教学让课堂绽放活力,让学生跳出“题海”、自主投入、寻找关联、深度思考,达成触类旁通、多题归一、深度学习的教学效果.
例3如图5,在正方形ABCD中,对角线AC和BD相交于点O,在线段AD上任意取一点F(不与点A,D重合),联结CF并延长交BA的延长线于点E,交AD于点G.探索线段CG,GF,EG的数量关系,用等式表示并证明.
变式1将例3中“如图5,在正方形ABCD中”改为“如图6,在ABCD中”,其余条件保持不变.当时,求和的值.

图5 图6
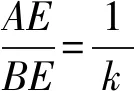
变式3在ABCD的条件下,线段CG,GF,EG的数量关系还成立吗?请说明理由.
3.3 结论开放化
孔子曰:“不愤不启,不悱不发,举一隅不以三隅反,则不复也.”学起于思,思源于疑.几何课堂中,当教师呈现“仅有条件没有结论”的开放性问题时,无疑是给学生创设了一个处于“愤悱”状态的场域.比如教师呈现如下问题:
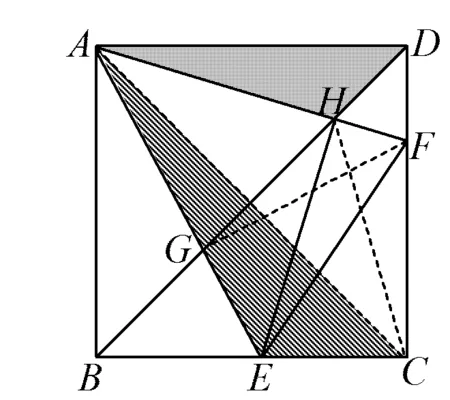
图7
例4如图7,在正方形ABCD中,E,F分别是BC和CD上的一点,联结AE和AF,分别交对角线BD于点G,H,且∠EAF=45°.
1)你能从中得到哪些结论?
2)联结AC,CH,EH,FG,你能从中得到哪些结论?
通过学生探索研究,发现了如下有价值的一些结论,并得到了证明:
①Rt△AEH和Rt△AFG均为等腰三角形.
②点A,B,E,H共圆;点C,E,H,F共圆;点E,F,H,G共圆;点A,D,F,G共圆.


⑤在Rt△ABD中,GH2=BG2+DH2,△ABH∽△GAH∽△GDA.
此时,学生的心扉被打开,探究的热情被激活,源于问题解决的创新思维被激发,这样开放的变式教学让学生在任务驱动下发现问题、主动建构、思维争辩、启迪智慧、畅思畅想,使课堂充满生趣,充满孜孜不倦的探索.
3.4 图形拓展化
结构化、系统化设计让学生能见“树木”,更能见“森林”,做到化“碎”为“整”.教师通过层次化、递进式的图形拓展(如图8),由“有公共顶点的两个等边三角形”出发,经历“有公共顶点的两个等腰三角形”“有公共顶点的两个等腰直角三角形”“有公共顶点的两个正方形”的变式拓展,引导学生形成知识结构、方法结构和内在的逻辑关系结构.
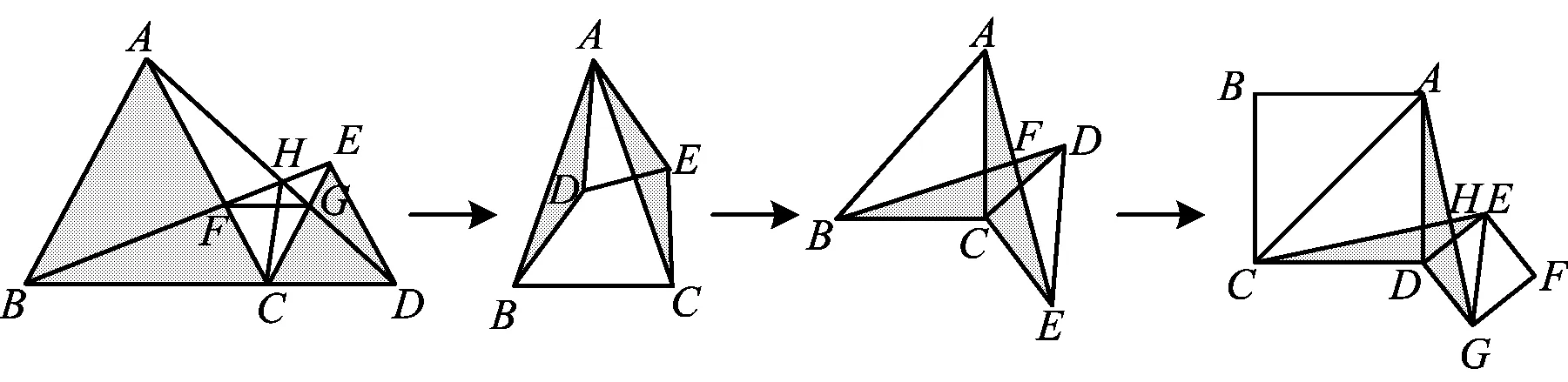
图8
教贵引导,学在领悟.笔者通过“逆向化、一般化、特殊化、开放化、拓展化”的变式策略,同时关注变式的“目的性、关联性、逻辑性、结构性”,引导学生深度参与,关注问题之间的多向联系及内在逻辑,主动探究,深度感悟,让学生在几何学习中自觉形成新的认知结构和心智图式.
4 一题多解,掌握通法,提炼优法
一题多解有利于调动学生的学习积极性,有利于学生对知识的掌握和厘清解题线索,有利于培养思维的广度和深度,有利于培养学生的创新思维和解题能力.一题多解也是几何教学的常用方法,但在实际教学中,很多教师采用了一题多解后,往往忽视了通性通法的梳理,忽视了最优方法的提炼,“热热闹闹”讲了诸多解法,由于没有重点,导致学生能掌握得甚少.我们来看一则案例:

图9

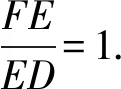

图10 图11 图12 图13
方法2如图11,过点D作DG∥AC交AB于点G,在△ABC中,由DG∥AC得“平A型”,△DFG中,由AE∥DG得“平A型”,求解可得.
方法3如图12,过点A作AG∥DF交BC于点G,在△BDF中,由AG∥DF得“平A型”,△ACG中,由AG∥DE得“平A型”,求解可得.
方法4如图13,过点A作AG∥BC交DF于点G,在△BDF中,由AG∥BD得“平A型”,又由AG∥DC得“平8型”,求解可得.
方法5分别过端点B,C,F作平行线,各有2种不同解法.
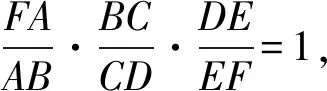
教师展示的6种解法对培养学生的思维和解题能力有一定的帮助,课后笔者随机找了8位学生座谈,结果显示:有5位学生表示“了解了6种解法,但是脑子里似乎有点混乱”;有2位学生表示“听懂了2~3种解法”;有1位基础相对薄弱的学生表示“一种解法都没搞懂”.
案例反思在上课前,教师要对方法先进行归类整理,梳理解决这一问题的通性通法是“添平行线法”:一类是过条件中的“特殊点”添平行线,如过点D或点A添平行线;另一类是过“端点”添平行线,如过点A或点B或点C添平行线.在上课中,教师要落实“添平行线法”的归类梳理,并引导学生在诸多方法中,首选过“特殊点”作平行线,即为最优方法,同时引导学生一起归纳得到:在每一种添法中,所添的平行线段都是两个基本图形(“A”字或“8”字)的公用线段,如方法1中,添辅助线DG在△ABC中构成基本图形“A”字型,同时在AF∥DG中构成“8”字型.这样的题后反思归纳有助于学生形成解题思路,解题路径更清晰,更有利于学生多向联系和正向迁移.
一题多解是提升几何教学效率,提升学生分析问题、解决问题能力的有效方法.但是,如果不注意梳理通性通法,不提炼最优方法,就无法走入学生心里,这样的一题多解,思维肤浅,深度学习很难形成.
几何教学离不开解题教学的策略研究.本文抛砖引玉,希望能给同行带来一些收获和思考,让我们一起在新课标和深度学习理念下进一步加强初中几何解题教学的策略研究,让学生的深度学习不断走向深入.
