基于ABAQUS的盘刷刷毛清扫性能分析

林 煜

（福建船政交通职业学院 汽车学院，福建 福州 350000）

清扫车在进行清扫作业时，盘刷刷毛作为与垃圾颗粒直接接触的部分，其清扫的性能如何，能否成功扫动垃圾颗粒，与垃圾颗粒之间的接触运动形式又是什么样的，这是值得探索的。

为了对盘刷刷毛的清扫性能进行分析，文中采用有限元方法来探讨刷毛对垃圾颗粒的作用情况，通过在ABAQUS软件中建立盘刷刷毛与垃圾颗粒的模型，模拟其清扫接触过程，从而得到刷毛与垃圾颗粒之间的运动受力情况，以此来说明刷毛对垃圾颗粒的清除效果。接着在不同触地深度下进行清扫，分析触地深度对于盘刷刷毛清扫性能的影响。

1 盘刷刷毛与颗粒的接触形式

清扫车在工作过程中，盘刷作为主要的工作装置之一，用来清扫清扫车两侧路面上的垃圾，而刷毛作为直接与垃圾颗粒接触的物体，其清扫性能的好坏直接关系到盘刷以及整辆清扫车的作业性能[1]。盘刷在扫动时，其刷毛与垃圾颗粒之间接触的形式一般分为两种，切式清扫和弹式清扫，两者的所受的作用力和发生的形变不同。

由于盘刷刷毛切式清扫与弹式清扫的特点不同，它们所适用的路况也就不同。在垃圾密度高的路面，应采用切式清扫；在垃圾密度较低的路面上，宜采用弹式清扫。本文所研究的清扫车一般常用在城市道路，主要清扫的对象为质量较轻的常见垃圾，因此，采用弹式清扫。

2 盘刷刷毛与颗粒的建模方法

刷毛与颗粒的接触是非常复杂的非线性接触问题，另外，垃圾颗粒与不同的路面之间的接触情况也不同。在干燥路面，可采用库伦摩擦定律进行计算；而当路面潮湿或者有泥土等复杂情况时，一般方法很难准确计算分析盘刷刷毛与路面及垃圾颗粒之间的受力和运动情况，因此，对模型的简化提出四点假设：

（1）清扫车盘刷所清扫的路面是平坦整齐的平面；

（2）盘刷刷毛与地面垂直，且在垂直于地面的平面内发生形变[2]；

（3）盘刷所清扫的垃圾颗粒具有一般的几何外形；

（4）盘刷刷毛与垃圾颗粒，垃圾颗粒与地面均充分接触且满足基本物理理论。

在上述假设条件下，为了便于分析，本文把垃圾物体简化成一个与地面充分接触的不规则体。图1为第j根刷毛与第i个垃圾颗粒接触的受力分析图。其中，1和2分别为颗粒与地面的接触点；aj为接触点3与点2之间的水平距离；hj为垃圾颗粒与刷毛的接触点3到地面的高度；颗粒与地面之间的摩擦系数为μ。

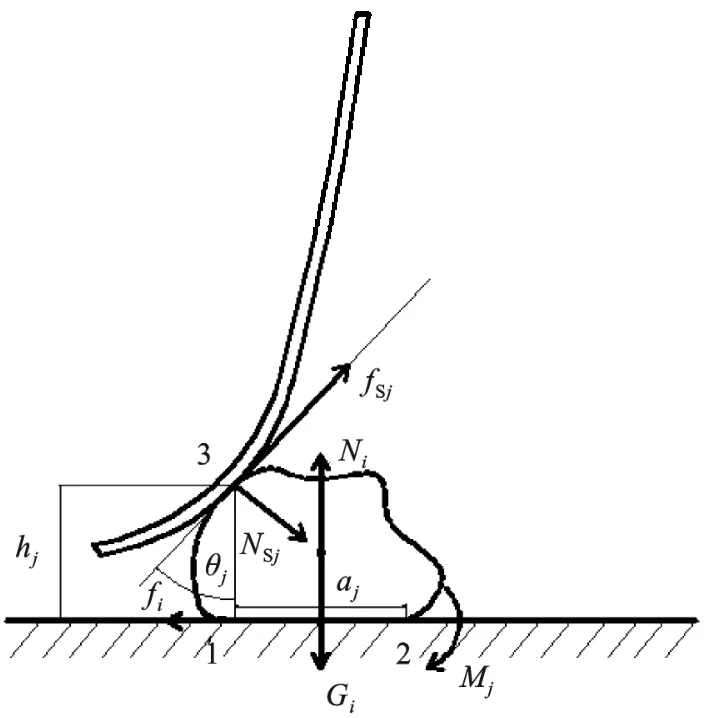
图1 刷毛与垃圾颗粒接触时的受力分析

当盘刷开始工作时，刷毛运动与垃圾颗粒形成接触并发生形变，之后如图所示与颗粒在点3处形成点接触，垃圾颗粒受到变形刷毛给予的接触压力NSj和两者间的摩擦力fSj，与此同时，垃圾颗粒也受到自身的重力Gi，地面给予的支持力Ni以及水平方向上的摩擦力fi，在外力的共同作用下，垃圾颗粒产生了一个绕着端点2的顺时针转矩Mj[3]。假设Fj为盘刷刷毛给予垃圾颗粒的清扫力，则通过受力分析可以得到

刷毛在水平方向上的清扫力为

刷毛在竖直方向上的清扫力为

式中，θj为刷毛与颗粒的接触点3的刷毛切线方向与竖直方向之间的夹角。

垃圾颗粒绕着端点2的顺时针转矩为

通过上述分析可以看出，刷毛给予垃圾颗粒的水平方向和竖直方向上的清扫力以及垃圾颗粒所受到的外力引起的转矩决定了刷毛能否成功扫动垃圾物。也就是盘刷能否完成有效清扫取决于水平清扫力FX和绕端点2的转矩M。

根据受力情况，可以得出垃圾颗粒被成功清扫的临界条件为[4-5]

式中，n为与垃圾颗粒i接触的刷毛总数；xi为垃圾颗粒i的重心与2点之间的水平距离。只有在满足上述条件之一，垃圾颗粒才能被成功清扫，视为有效清扫。

3 盘刷刷毛与颗粒ABAQUS分析

在满足几点假设的前提下，将盘刷刷毛与垃圾颗粒的接触模型进行了简化，由于盘刷刷毛对于垃圾物体的清扫过程中盘刷刷毛的变形情况无法获得，而且在刷毛与垃圾颗粒的接触过程中，刷毛垃圾颗粒的接触点不断改变，不同位置的边界条件无法确定[4]。因此，为了更好地分析刷毛与颗粒的非线性接触问题，文中采用了ABAQUS有限元方法。

盘刷刷毛与垃圾颗粒的接触过程作为高度非线性问题，一方面刷毛与颗粒的接触区域未知，接触过程中位置形态不断变化，而且受到多个因素的影响，比如：材料、载荷等等[5]。另一方面，刷毛与颗粒之间的接触要考虑摩擦力的作用，而摩擦问题经常都是非线性无序的，很容易造成计算求解的不收敛，因此，创建合适的有限元模型是十分必要的，可以提高求解的效率。

为了更好地分析刷毛与颗粒的接触过程，本章将分别建立两个模型来模拟清扫过程，一个是盘刷刷毛不与地面接触，直接在位移载荷的作用下，与颗粒发生相互作用，另一个将对刷毛先施加不同的触地压力，即不同的触地深度，而后与颗粒接触。

3.1 刷毛直接与颗粒接触

在ABAQUS中建立盘刷刷毛与垃圾颗粒的简化二维接触模型，垃圾颗粒为不规则形体，故其重心的位置是无法确定的，为便于分析，将垃圾颗粒简化为正方形作为垃圾颗粒仿真模型。定义刷毛的长度250 mm，半径1 mm，设置与地面45°夹角，特征类型选择wire，其余保持默认。垃圾颗粒为边长30 mm正方形，类型为solid，在未接触前与刷毛之间相隔5 mm。

表2 垃圾颗粒设置

在初始分析步中将垃圾颗粒与地面接触的左右两个端点1、2进行约束，令其U1=U2=UR3=0，即在X方向、Y方向的位移为0，以及在平面内不发生转动。在刷毛的设置上，对其上端点进行约束，设置U2=UR3=0，即刷毛在Y方向上和平面内的转动自由度都为0。

在step1中，在刷毛的上端点施加水平方向的位移载荷[6]。刷毛与垃圾接触后，step1结束，进入step2，在该分析步中继续施加水平方向上的载荷。随着位移的增加，刷毛下端点与地面分离，直到与垃圾的4点接触，此时step2结束，进入step3，在该分析步中仍旧施加水平向右的位移载荷，直到刷毛与垃圾上表面分离。

图2 刷毛与垃圾颗粒及地面的模型

另外，设置刷毛下端点与地面、刷毛与垃圾颗粒左上端点4、刷毛下端点与颗粒上表面三处接触类型皆为点面接触。其中，刷毛沿着颗粒左上端点4运动时，刷毛位置不断移动，但是与颗粒的接触点保持不变，因此，可视为点面接触，而刷毛与地面以及颗粒上表面的接触位置始终为其下端点。这三处接触的切向属性均为penalty，切向摩擦系数分别设为0.5、0.2、0.2，而法向摩擦属性设为hard，接触面约束施加算法采用默认的default。

我说：“其实这也意味着你前期就已经做好了很多。”“也许是这样，顶尖的定义很难说，但是至少从其他行业来看，可能拿到MS在葡萄酒行业是比较顶尖的。当你在某一个行业比较顶尖的时候，你有更多的机会去认识其他行业顶尖的人。至少是那个行业的人认可的，这对我来说是很有意义的事情。因为抛开葡萄酒不说，这让你的眼界更宽广一点，让你想东西会更多一点，层次感会更强一点。这可能是拿到MS比较重要的一个变化。其实生活和工作没有什么变化，忙会更忙。但工作还是那些工作，还是我非常重要的一部分。”

分别对刷毛、地面以及垃圾颗粒进行网格的划分，建立的模型如图3—图4所示。

图3 颗粒左右端点1、2水平方向上的受力情况

在模型中，刷毛在水平方向的位移载荷作用下向右运动。

在得到颗粒与地面接触点的受力数据后，分别对颗粒与地面的左右接触端点在水平方向和竖直方向上的受力进行曲线拟合，得到的结果如图3和图4所示。其中P1、P2分别代表点1、点2，RF1为水平方向的力，RF2为竖直方向的力。第一条竖直线段之前表示刷毛在地面运动，还未与垃圾颗粒发生接触，两条竖直线段之间的部分表示刷毛沿着颗粒的左上端点4进行移动，两者有接触，第二条竖直线段之后的部分表示刷毛离开颗粒左上端点，其下端点与颗粒的上表面形成接触，直至刷毛与颗粒完全脱离，清扫过程结束。

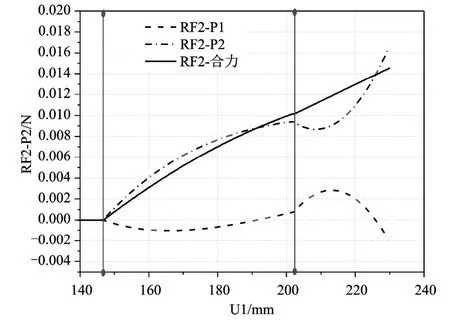
图4 颗粒左右端点1、2竖直方向上的受力情况

观察图4可以看到，刷毛与垃圾颗粒左上端点4接触的过程中，颗粒与地面接触的端点1和2受到的地面给予的力为负值，即水平向左，反过来说，刷毛给予颗粒水平向右的一个清扫力，和运动方向同向。且随着刷毛沿着颗粒左上端点不断移动，1和2点所受的力以及它们的合力不断变大，直到刷毛与左上端点即将分离时，达到最大值。在第二条竖直线段之后，即刷毛下端点与颗粒上表面接触，随着刷毛继续移动，刷毛作用在颗粒上的水平合力不断减小，在左端点1点上的分力在刷毛运动到颗粒上表面后半段时甚至改变了方向，阻碍颗粒被刷毛向前扫动，这是因为刷毛在颗粒上表面运动时，对颗粒有一定的压力，在运动到后半段时，由于弹性形变，会对颗粒产生一个向后推动的趋势，但总体来说，刷毛作用在颗粒的水平清扫力始终是正的。

图4中的两条竖直线段之间，地面给予颗粒的Y方向上的支持力越来越大，也就是说刷毛作用在颗粒上的压力越来越大。在与地面接触的左右端点1、2上，点1的支持力为负值（只有在刷毛即将与颗粒左上端点4脱离时才变为正值，因为此时刷毛即将与颗粒上表面接触，对颗粒的左半部分压力变大，导致颗粒有一个向后转动的趋势，阻碍颗粒向前的转动），点2的支持力为正值，这样一来，刷毛对颗粒就形成了一个顺时针的转矩，有利于刷毛扫动颗粒。在刷毛与颗粒上表面接触的部分，刷毛作用在颗粒上的压力继续变大，点1受到的地面支持力在正方向上先变大，之后减小变为负值并增大，而点2受到的地面支持力为始终为正值，有一个先减小后变大的变化过程，这些都符合了刷毛在颗粒上表面从左端移动到右端所引起的变化规律，直至两者脱离，清扫运动结束。

图5为刷毛对颗粒进行清扫时对其产生的绕着右下端点2的转矩，在刷毛与颗粒的左上端点4的接触过程中，刷毛一直对颗粒形成一个顺时针的转矩，有利于刷毛扫动垃圾颗粒，直到刷毛即将与颗粒的左上端点脱离，这时转矩变为逆时针，阻碍颗粒朝着清扫的方向转动。在刷毛与颗粒上表面接触中，逆转矩先变大后变小，之后又变成顺时针转矩，因为刷毛从颗粒上表面左端一直移动到了右端，变化趋势符合运动规律。

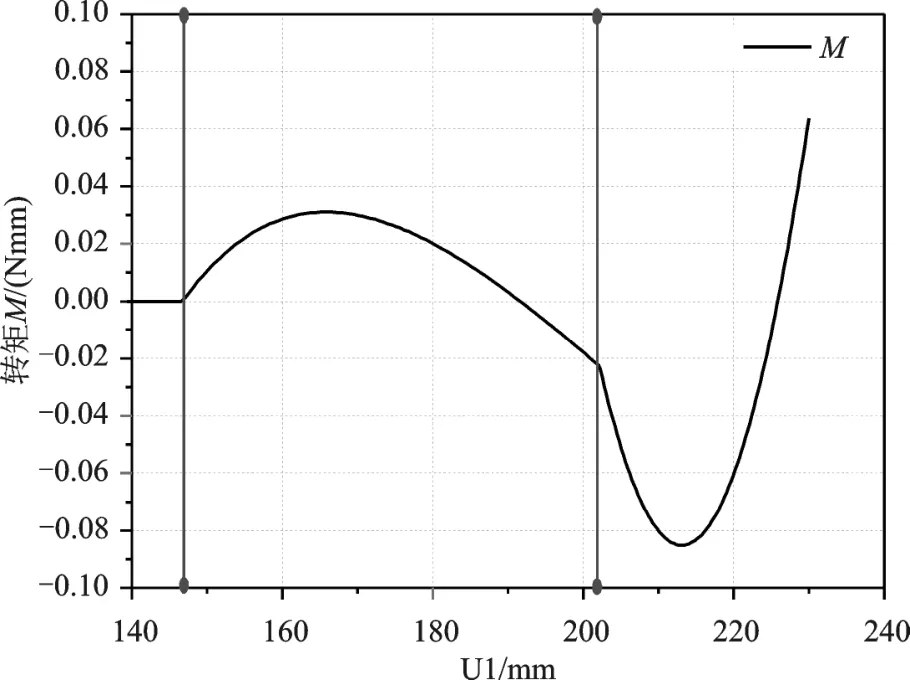
图5 刷毛对垃圾颗粒的滚动转矩

通过对比可以发现，单根刷毛对垃圾颗粒作用所产生的绕着左下端点2的转矩远小于颗粒自身重力在端点2的逆转矩0.5amg，即不满足颗粒在刷毛作用下发生转动的临界条件。所以，垃圾颗粒是否能够被刷毛成功清扫，取决与刷毛的水平清扫力FX，只有颗粒在水平方向上受到的清扫力大于颗粒受到的地面的摩擦力f，垃圾颗粒才能在地面上发生移动，即

式中，μ为地面和垃圾颗粒之间的摩擦系数；FX为刷毛对颗粒的水平清扫合力；FY为地面对垃圾颗粒的支持力。

为了能够更直观地分析刷毛对颗粒的作用，以及为下一节触地深度的分析做铺垫，本节在这里设定一个临界的摩擦系数μX，则

式中，n为刷束中刷毛的根数，在这里，取n值为10。

在清扫时，若垃圾颗粒与地面的实际摩擦系数μ小于临界摩擦系数μX，则说明垃圾颗粒可以被盘刷刷毛成功清扫。因此，可以通过计算得到临界摩擦系数μX与水平方向上移动的距离U1的关系，如图6所示，以此来判断垃圾颗粒是否被成功清扫。

从图6可以看到，在刷毛触地深度为零，即为自由状态下，直接对垃圾颗粒进行清扫的情况下，刷毛从与垃圾颗粒的左上端点接触，到与其上表面接触，直达与颗粒完全脱离，这个过程中，临界摩擦系数μX的最大值为0.22，也就是说，当垃圾颗粒与地面之间的实际摩擦系数μ小于0.22时，就可以被盘刷刷毛扫动，即有效清扫。

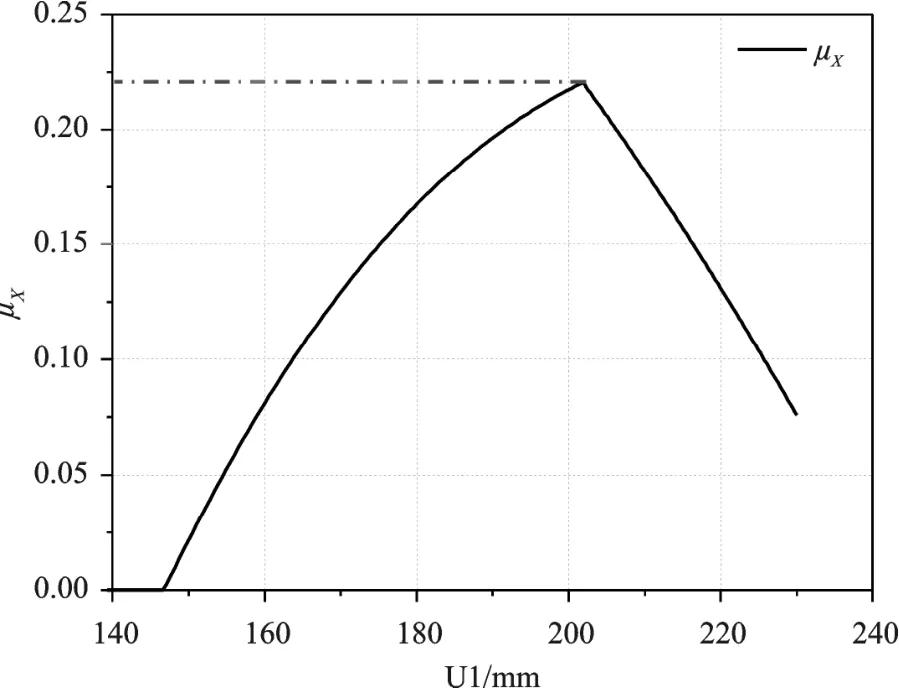
图6 临界摩擦系数μX的变化趋势

3.2 刷毛触地后与颗粒接触

刷毛在与垃圾颗粒接触之前，都会先有一定程度上的压缩变形，这是由盘刷自身的重量以及盘刷触地压力调节机构所决定的。在合理的触地压力下，刷毛具有一定的触地深度，从而发生形变。合理的压缩状态下的刷毛对颗粒进行清扫时，会把一定的弹性势能传递给垃圾颗粒，从而更有助于垃圾被成功清扫。

通过给予刷毛竖直方向上10 mm、20 mm、 30 mm等不同的触地深度，分别模拟刷毛与颗粒的接触过程，可以得到在不同触地深度下，垃圾颗粒受到的水平方向上的合力，即盘刷刷毛对颗粒的水平清扫力，如图7所示。从图中可以看出，随着触地深度的加大，刷毛给予垃圾颗粒的水平方向上的清扫力也在不断增大，这是由于刷毛压缩变形的一部分弹性势能释放，传递给了垃圾颗粒，转变成清扫力，有利于颗粒被扫动。但是可以观察到，清扫力增大的趋势在减小，因此，可以说明，过大触地深度在增加刷毛磨损的同时也不利于刷毛对颗粒的成功清扫，所以存在一个合理的触地深度值，对提升刷毛的清扫性能十分关键。

图7 压缩状态下刷毛的水平清扫合力

本节所建立的模型中，刷毛在不同触地深度下，所求得的垃圾颗粒受到的绕着右下端点2的转矩依旧小于颗粒自身重力在端点2的逆转矩0.5amg，因此，仍旧不满足颗粒在刷毛作用下发生转动的临界条件。所以，垃圾颗粒是否能够被刷毛成功清扫，还是取决与刷毛的水平清扫力FX。

为了直观地说明触地深度对于清扫力的影响，采用上文中的临界摩擦系数μX，通过在不同的触地深度下，分别求出垃圾颗粒在竖直方向和水平方向上所受到的力，进而求出临界摩擦系数，得到临界摩擦系数与刷毛触地深度的变化趋势，如图8所示。

图8 临界摩擦系μX数与触地深度的关系

从图8中可以观察到，前期随着刷毛触地深度的增加，临界摩擦系数μX也在不断变大，在触地深度60 mm左右时，达到最大值0.72，即当垃圾颗粒与地面之间的实际摩擦系数μ小于0.72时，均可以被盘刷刷毛成功有效清扫。之后，触地深度继续增大，临界摩擦系数反而逐渐变小，盘刷刷毛的清扫性能降低，这是因为过大的触地深度会使刷毛形变增大，给予垃圾颗粒的压力也不断变大，这会增大颗粒与地面的摩擦力，加大了清扫难度，同时触地深度变大会加大刷毛的磨损程度。

4 小结

本章目的在于了解盘刷刷毛清扫的过程，采用有限元方法对盘刷刷毛的清扫性能进行分析，在满足所提出的四点假设的基础上，对刷毛与颗粒的模型进行了简化。但是由于盘刷刷毛与垃圾颗粒的接触过程作为高度非线性问题，对其过程的分析还是存在较大困难，一方面是因为在清扫过程中盘刷刷毛的变形情况无法知晓，另一方面在刷毛与垃圾颗粒的接触过程中，刷毛沿着颗粒发生滑动，其与垃圾颗粒的接触点不断在变，不同位置的边界条件不同，无法确定，因此，建立合理的有限元模型十分关键。

为了更好地分析刷毛与颗粒的接触过程，本章在ABAQUS软件中分别建立了两个模型来模拟清扫过程，一个是盘刷刷毛不与地面接触，直接 在位移载荷的作用下，与颗粒发生相互作用，另一个是对刷毛先施加不同的触地深度，而后与颗粒接触。在模拟接触过程后，得到了刷毛对于垃圾颗粒在水平方向和竖直方向上的清扫力，以及颗粒沿着运动方向受到的转矩。在对受力数据进行分析之后，得到了清扫力及力矩的变化规律，之后，在不同触地深度的对比之下，得到刷毛的最佳触地深度值。