不均等层厚划分的功能梯度圆筒的有限元分析

胡雷雨，薛恺文，王 政

(中国矿业大学力学与土木工程学院，江苏 徐州 221116)

0 引言

煤炭作为我国能源供给结构的主体，已经成为国民经济高速发展的重要基础，在短时间内其地位不会发生动摇。但随着几十年的不断开采利用，我国浅部可开发煤炭资源的急剧减少，使得人们不得不将目光转向了深部地下，深部煤炭资源的开采已经成为了必然趋势，立井的建设将成为今后煤炭行业一个主要的工作方向。但是随着开采深度的不断增加，深部巨大的围岩压力以及复杂的地层环境对支护结构的承载力提出了更高的要求，如何有效提高井壁的承载能力引起了许多学者的关注。

目前为提高井壁的承载能力，现有解决方法主要有提高混凝土材料强度、增加井壁厚度以及使用特殊结构。针对提高材料强度来提高立井井壁的承载能力的方法，姚直书等[1]学者曾提出混凝土强度提高10 MPa，则井壁承载力将提高约13.8%。而对于增加井壁厚度提高井壁的承载能力的方法，张宁等[2]学者曾提出对于延伸至1 000 m深的竖井，衬砌厚度增加10 mm，钢筋混凝土将增加1%的总成本，而普通混凝土将增加0.25%的总成本。可见，此种方法会增加施工成本。同时，传统均质井壁在承受外压作用下，井壁内侧会出现环向应力集中的现象，且井壁外侧混凝土的承载能力却得不到有效发挥，因此上述两种方法提高井壁承载力的范围十分有限，并且将会造成材料的浪费。因此，较多的国内外学者将功能梯度材料引入了立井井壁。

功能梯度材料(FGM)是一种组成和性能在空间上呈连续变化的新型复合材料，最早是由新野正之与平井敏雄[3]等日本科学家于1987年提出。最初是为了解决航空航天领域中极端条件下材料的隔热问题，后来被广泛的应用于航天、石油天然气、机械、核反应等领域。功能梯度概念引入土木工程领域较晚，目前仍处于发展阶段。随着深部地下的开发，一些学者提出将功能梯度材料与立井井壁等结构结合，利用功能梯度材料的材料性能在空间连续变化的特性来缓解结构中应力集中现象，从而达到“柔性让压”的效果，但这种使材料属性连续变化的特点在实际工程中很难实现。针对这一不足，不少学者将层合模型的理念引入实际工程中来解决这一问题。张宁等[4-5]提出了一种多层功能梯度立井井壁结构及其制作方法，即将立井井壁分为多层同轴圆筒结构分层赋予不同材料，从而使材料弹性模量在半径方向上达到近似连续变化。上述井壁结构仅仅满足了力学承压要求，为了应对深部地层中的复杂环境，李德春等[6]提出一种新型功能梯度井壁结构，通过增加抗渗、抗水压、抗腐蚀、抗火等同轴混凝土功能层赋予结构多种功能特性。此外数值模拟方面，许冲[7]利用ABAQUS对于上述多层同轴的功能梯度井壁结构的受力变形规律进行了数值模拟，宋日新[8]研究了由两项材料按特定的体积分数组成的功能梯度圆筒，在弹性状态下运用ANASYS进行受内压的数值模拟，并与理论分析进行了比较，验证了其解析解的正确性。上述的功能梯度圆筒结构的层合模型都是等分的划分形式，即由多层同轴等厚度圆筒组成，并基于不同形式函数，使得圆筒结构的弹性模量沿半径方向发生近似连续变化。

但以上的层合模型均是基于普通均等划分层厚的情况(即每层同轴圆筒的厚度都相同)，对于井壁不均等层厚划分的情况(即每层同轴圆筒的厚度并不相同)目前尚没有学者进行相关深入研究，本文则通过建立N层不均等分功能梯度立井井壁的层合模型，借助ABAQUS有限元软件进行数值模拟，探究了在沿径向弹性模量线性变化(内小外大)的N层功能梯度圆筒中，4种不均等层厚划分与普通均等层厚划分相比井壁内部Mises应力和位移的差别，并通过改变划分层数N来进一步探究层数的变化对上述由不同划分层厚方式引起的差别的影响，最后验证了弹性模量沿径向线性变化情况下所得结论在沿径向方向弹性模量按照其他的函数变化形式中的适用性与普遍性。

1 有限元模型的建立

为了研究不均等层厚划分层合模型下功能梯度立井井壁力学特性变化，本次模拟我们针对井壁沿径向弹性模量的变化共设计了3种弹性模量函数(线性函数、指数函数、幂函数)，并就每种弹性模量变化分别设计了3层,6层,10层的功能梯度井壁，并针对每种情况研究了在5种不同层厚划分形式(中间层厚大两边层厚小、中间层厚小两边层厚大、均匀层厚、从内层到外层各层厚度依次增大、从内层到外层各层厚度依次减小)，共计45个模型，具体模型参数如表1所示。

表1 模型参数

使用ABAQUS进行数值模拟计算，采用二维平面模型，由于井壁为轴对称结构，为了简化模型加快运算速度，取1/4结构研究，井壁截面为对称边界，采用定向支座约束，在井壁外侧施加荷载，单元类型为CPE4R。圆筒的5种不同层厚划分形式(此处以6层井壁模型为例)：中间层厚大两边层厚小，如图1(a)所示；中间层厚小两边层厚大，见图1(b)，均匀层厚，见图1(c)；从内层到外层各层厚度依次增大，见图1(d)；从内层到外层各层厚度依次减小，见图1(e)。

工况J1：从内层到外层各层厚度依次减小。

工况J2：从内层到外层各层厚度依次增大。

工况J3：中间层厚大两边层厚小。

工况J4：中间层厚小两边层厚大。

工况J5：均匀层厚。

由内外边界弹性模量拟合得到如下3种不同形式弹性模量变化函数：

2)指数变化：E(r)=247 44e2.682 2×10-4r。

3)幂函数变化：E(r)=3 694.9r0.315。

5种工况下45个模型各层厚度分布见表2～表4。

表2 3层功能梯度井壁各层厚度分布

表3 6层功能梯度井壁各层厚度分布

表4 10层功能梯度井壁各层厚度分布

2 仿真结果分析

本文将主要分析弹性模量沿径向线性变化下不同层厚划分对功能梯度井壁结构力学特性的影响。根据ABAQUS数值模拟结果，我们将依次选取3层，6层和 10层分布的功能梯度井壁为研究对象。之后将进一步介绍其他两种弹性模量变化函数形式下的模拟结果。

2.1 弹性模量沿径向线性变化下的3层功能梯度圆筒仿真结果分析

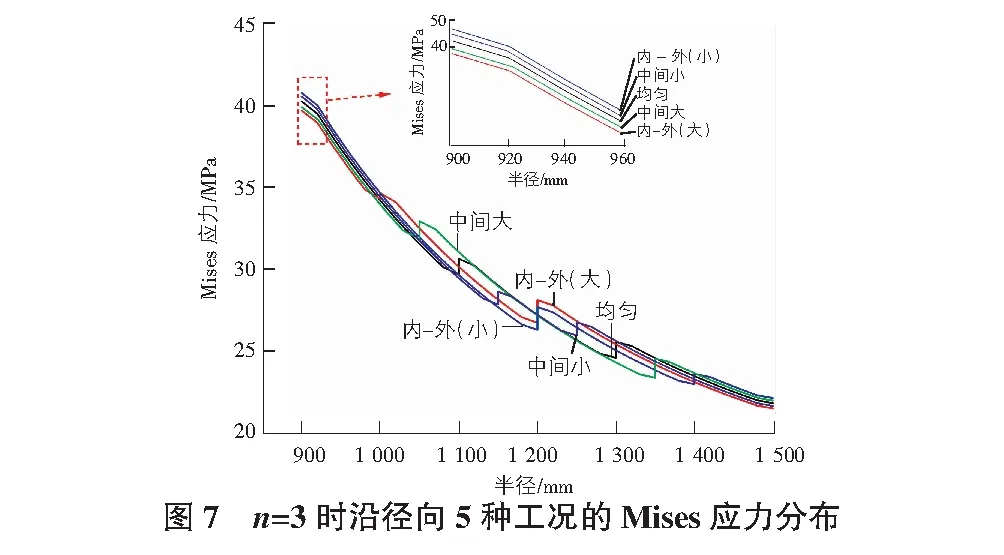
当功能梯度井壁划分为3层时，5种不同层厚划分工况下功能梯度井壁截面的Mises应力分布云图如图2～图6所示。由图可知，在外侧15 MPa的均布荷载的作用下，功能梯度井壁的内部Mises应力自外侧向内侧逐渐增大，应力最终在井壁最内层达到最大值。此外，通过比较不同层厚划分工况中的最大Mises应力和最小Mises应力可知，最大Mises应力满足：J1>J4>J5>J3>J2，最小Mises应力满足：J1>J3>J5>J4>J2，但这5种工况下井壁的位移云图基本相同(见表5)。沿径向5种工况的Mises应力分布图及位移分布图见图7，图8。

表5 n=3时各工况得到的最大应力、最小应力以及最大位移

2.2 弹性模量沿径向线性变化下的6层功能梯度圆筒仿真结果分析

当功能梯度圆筒划分为6层时，沿径向方向5种不同层厚划分工况下功能梯度井壁结构的Mises应力和位移分布，如图9，图10所示。由图可知，最大Mises应力满足：J4>J1>J5>J2>J3，最小Mises应力满足：J3>J1>J5>J2>J4，但这5种工况下圆筒的位移云图的分布和数值大小基本相同(见表6)。

表6 n=6时各工况得到的最大应力、最小应力以及最大位移

2.3 弹性模量沿径向线性变化下的10层功能梯度圆筒仿真结果分析

当功能梯度圆筒划分为10层时，沿径向方向5种不同层厚划分工况下功能梯度井壁结构的Mises应力和位移如图11，图12所示。由图可知，最大Mises应力满足：J1>J4>J5>J2>J3，最小Mises应力满足：J1>J3>J5>J4>J2，同时这5种工况下圆筒的位移云图的分布和数值大小基本相同(见表7)。

表7 n=10时各工况得到的最大应力、最小应力以及最大位移

线性函数3层：最大Mises应力：J1>J4>J5>J3>J2，最小Mises应力：J1>J3>J5>J4>J2，位移：基本相同。

线性函数6层：最大Mises应力：J1>J4>J5>J2>J3，最小Mises应力：J3>J1>J5>J2>J4，位移：基本相同。

线性函数10层：最大Mises应力：J1>J4>J5>J3>J2，最小Mises应力：J1>J3>J5>J4>J2，位移：基本相同。

不难发现，与功能梯度井壁划分为3层和6层时相比较，5种工况的最大Mises应力大小顺序满足一定规律，即J1，J4>J5>J2，J3。同样，5种工况的最小Mises应力大小顺序也满足一定规律，即J1，J3>J5>J2，J4，并且随着层数的增加，各工况下圆筒结构内部的最大Mises应力逐渐减小，最小Mises应力逐渐增大，并且使得不同工况的Mises应力数值差距越来越小。对于位移而言，5种工况下 的结构中各点位移基本相同，位移分布曲线都呈现出凹型，即位移分布沿井壁内部向外部先减小后增大。出现这种现象的原因是井壁的内边界和外边界为临空面，它们的变形没有受到其他物体约束，因此导致其内外边界位移较大；但处于井壁内部的各点的变形受到周边部分的限制，不能自由变形移动，并且越远离内外边界这种限制也就越发显著，从而导致内部各点位移较小，在井壁位移分布曲线上也就表现为沿井壁内部向外部先减小后增大的凹型分布。同时随着层数的增加，各工况的最大位移也逐渐增大，但增长量很小，不超过0.01 mm。

2.4 弹性模量沿径向指数和幂函数变化下的模拟结果概况

本文对沿径向弹性模量按照指数和幂函数变化的井壁情况同样进行了仿真模拟和结果分析，与上文中井壁的弹性模量按线性变化得出的结论基本吻合，5种工况中的最大Mises应力大小顺序满足J1,J4>J5>J2,J3。同样，5种工况中的最小Mises应力大小顺序也满足J1,J3>J5>J2,J4，并且随着层数的增加，各工况下圆筒结构内部的最大Mises应力逐渐减小，最小Mises应力逐渐增大，并且使得各工况中的Mises应力数值差距越来越小。对于位移而言，5种工况下的结构中各点位移基本相同，并且随着层数的增加，各工况的最大位移也逐渐增大，但增长量很小(不超过0.01 mm)。

指数函数3层时，最大Mises应力：J1>J4>J5>J3>J2，最小Mises应力：J1>J3>J5>J4>J2。

指数函数6层时，最大Mises应力：J4>J1>J5>J2>J3，最小Mises应力：J3>J1>J5>J2>J4。

指数函数10层时，最大Mises应力：J1>J4>J5>J2>J3，最小Mises应力：J1>J3>J5>J4>J2。

幂函数3层时，最大Mises应力：J1>J4>J5>J3>J2，最小Mises应力：J1>J3>J5>J4>J2。

幂函数6层时，最大Mises应力：J4>J1>J5>J3>J2，最小Mises应力：J1>J3>J5>J2>J4。

幂函数10层时，最大Mises应力：J1>J4>J5>J2>J3，最小Mises应力：J3>J5>J1>J4>J2。

不难看出，在3层，6层，10层层数下，5种工况中的最大Mises应力大小顺序均满足J1，J4>J5>J2，J3；最小Mises应力大小顺序也均满足J1，J3>J5>J2，J4，并且随着层数的逐渐增多，不同的层厚划分工况中的Mises应力数值差距越来越小。造成这种现象的原因，主要是随着划分层数的增加，每层厚度逐渐减小，整体上拟合弹性模量的变化函数也就越来越精确，井壁沿径向的弹性模量也就越接近连续变化，因此可以合理推测当层数N足够大时，就实现了真正意义上的功能梯度材料，即组成和性能在空间上呈连续变化。与此同时，功能梯度的“柔性让压”特性也在随着层数的增加而逐渐增强，从而缓解井壁内侧环向应力集中的现象，降低结构中的最大应力。从位移方面，5种工况下的结构中各点位移基本相同，位移分布曲线都呈现出凹型，即位移分布沿井壁内部向外部先减小后增大。出现这种现象的原因是井壁的内边界和外边界为临空面，它们的变形没有受到其他物体约束，因此导致其内外边界位移较大；但处于井壁内部的各点的变形受到周边部分的限制，不能自由变形移动，并且越远离内外边界这种限制也就越发显著，从而导致内部各点位移较小，在井壁位移分布曲线上也就表现为沿井壁内部向外部先减小后增大的凹型分布。但随着层数的增加，各工况的最大位移逐渐增大，这也正好印证了随着层数的增加，功能梯度的“柔性让压”特性逐渐变得显著。同样，在圆筒结构中采用其他的弹性模量的变化函数，除了缓解应力集中现象的效果有所差别，但是得出的结论与弹性模量沿径向线性变化的结果基本保持一致。

最后，通过综合最大Mises应力和最小Mises应力来分析，可以发现工况J2(从内层到外层各层厚度依次增大)的层厚划分为5种层厚划分工况中最优的(即工况J2中的最大Mises应力和最小Mises应力都是5种工况中较小的)，并且这种优势在层数越少的情况下反映的更加明显，因此这种特性十分有利于推广功能梯度井壁的实际运用。实际工程中由于受到施工条件的限制划分层数不可能过大，否则会导致每层厚度过小而不便于浇筑混凝土，因此为了兼顾施工便利需要和功能梯度特性，采用从内层到外层各层厚度依次增大的层厚划分则可以有效的解决这个问题，能在有限的划分层数下相比于其他层厚划分方式更能发挥功能梯度井壁的“柔性让压”特性，有效缓解井壁内侧环向应力集中现象，同时功能梯度井壁也避免了各处均采用同样高强度混凝土而造成不必要成本增加。

3 结论

1)5种工况中的最大Mises应力大小顺序满足J1，J4>J5>J2，J3；最小Mises应力大小顺序满足J1，J3>J5>J2，J4，并随着层数的逐渐增多，不同的层厚划分工况中的Mises应力数值差距越来越小。

2)5种工况下的结构中各点位移基本相同，并且随着层数的增加，各工况的最大位移也逐渐增大，但增长量很小(不超过0.01 mm)。

3)综合最大Mises应力和最小Mises应力来分析，可以发现工况J2(从内层到外层各层厚度依次增大)的层厚划分为5种层厚划分工况中最优的(即工况J2中的最大Mises应力和最小Mises应力都是5种工况中较小的)。

4)若在功能梯度井壁实际运用中，由于受到施工条件的限制划分层数不可能过大时，采用从内层到外层各层厚度依次增大的不均等层厚划分形式，可以在有限的划分层数下相比于其他层厚划分方式更能发挥功能梯度井壁的“柔性让压”特性，有效缓解井壁内侧环向应力集中现象。