对空间探测雷达网的多机协同航迹欺骗干扰方法

赵艳丽 李 宏 杜嘉薇 徐 阳

(63891部队 洛阳 471000)

1 引言

组网雷达是现代防空和反导战场中的重要装备。组网雷达凭借多频段、多体制及信息融合的优势，在防空或反导中，能够对突防的飞机或者导弹进行探测、定位、跟踪及识别，有效降低其突防概率[1–5]。

对组网雷达的多机协同的航迹欺骗干扰近些年受到广泛关注[6–12]。多机协同航迹欺骗干扰是指利用多架干扰机协同，利用数字射频存储器(Digital Radio Frequency Memory, DRFM)产生距离延迟假目标，对雷达网中各部雷达产生相互关联的虚假目标点迹；通过调整干扰机的航线及假目标转发延迟时间，使各部雷达形成相互关联的假目标航迹，进而诱惑敌方雷达网探测跟踪虚假航迹，降低雷达网对目标的发现概率，进而提升真实目标的突防概率。文献[6]最早提出多机协同航迹欺骗的基本概念，建立了多机协同飞行的航路规划模型。文献[7]进一步验证了多机协同航迹欺骗的可行性，文献[8]将最优控制理论引入航路规划问题中，提出了一种在线的实时控制技术。文献[9–16]从轨迹优化的或者干扰机数目优化的角度对多干扰机协同航迹欺骗进行了研究。文献[17]针对误差下的分布式组网雷达对虚假航迹的识别问题，提出了一种误差补偿机制。

以上的多机协同航迹欺骗干扰技术，都是以大气层内飞机类目标突防为背景，电子战干扰机具有动力系统和飞控系统，可以实时控制干扰机的运动参数。但是对于大气层外弹道中段突防的空间目标而言，其干扰机载体基本不具有动力系统和飞控系统，仅受地心引力作用，其运动轨迹仅由从母舱抛撒时的位置和速度决定，飞行期间无法改变其运动轨迹。所以，当前的多机协同航迹欺骗干扰技术无法直接应用到对空间目标的雷达网突防中。因此，如何对空间目标探测雷达网形成持续稳定的、不被融合中心识别剔除的高逼真欺骗航迹，是非常有难度、非常有挑战的一个问题，当前公开发表的文献中，尚未看到对此问题的研究。

本文提出了一种新颖的对空间探测雷达网进行多机协同航迹欺骗干扰方法。首先，从大气层外多机协同欺骗航迹的约束条件出发，基于简化问题找“特解”思想，通过巧妙设计多干扰机初始运动状态、使多干扰机弹道中段飞行过程中保持空间构型不变，进而使飞行过程中假目标航迹保持连续，解决了航迹欺骗干扰的关键技术难题。然后，推导计算了干扰机初始状态、干扰机的干扰延迟时间，给出航迹欺骗干扰的设计流程和实施流程。最后，以3部干扰机3部组网雷达为例进行了仿真实验，验证了本文方法的有效性。

2 多机协同航迹欺骗干扰理论研究

2.1 问题描述和分析

本文要研究的问题可以描述如下：对由多部相控阵雷达构成的空间探测雷达网，在其采用了数据融合抗干扰措施的前提下，采用多部弹道中段飞行的多干扰机协同对雷达网生成持续稳定的、不会被融合中心剔除的高逼真欺骗干扰航迹。

多干扰机对多部组网雷达进行干扰，需要首先满足干扰频段对准、干扰功率有效、复制的干扰信号精度满足需求等欺骗式电子干扰的常规约束。其次，多干扰机协同干扰还需考虑干扰机数量。通常情况下，为了不使欺骗航迹被识别，最好每一部雷达都有一部或多部干扰机负责对其干扰，因而，干扰机个数最好大于等于网中雷达的个数。最后，也是最重要和最困难的，是设计多部干扰机的相对运动态势以及干扰机的转发干扰延时时间。多干扰机能否在空间态势上、干扰延迟时间上精密配合，决定了对空间探测雷达网航迹欺骗的成败及质量。因此，本文需要重点研究多干扰机运动态势和干扰延迟时间的设计。

多干扰机想实现对空间探测雷达网的高逼真航迹欺骗干扰，须满足如下2个约束条件：

(1)各干扰机都依照弹道轨迹飞行。由于工程可实现性、干扰性价比等条件的约束，在本研究中，不考虑干扰机机动的可能性。在弹道中段干扰机仅受重力作用，干扰机服从“二体运动”方程，其轨迹由初始运动状态决定，这是受客观物理规律所支配的约束，是必须考虑的前提约束条件；

(2)干扰持续期间内，在各干扰机依照弹道轨迹高速飞行的情况下，任一时刻，多部雷达与对应干扰机所形成的多条射线必须有一个共同交点。该约束意味着可形成不会被融合中心剔除的协同假目标点迹，且协同假目标点迹可以保持连续，形成高逼真的协同假目标欺骗干扰航迹。

对于这2条约束，常规的思路是建立该问题的数学模型，但即便是在不考虑各种误差因素的理想情况下，粗略定性分析也会发现，存在如下困难：(1)干扰机的“二体运动”方程是非线性的微分方程组，无显式表达；(2)对一部干扰机的状态描述，需包含时戳、位置、速度、干扰延时时间等8个变量，M部干扰机则需至少8M维的变量。因此，对于一个如此复杂的情形，想建立一个统一的显式表达的数学模型，难度非常之大，另外即便能建立其数学模型，求其数学上的通解，几乎不具有可行性。

2.2 解决思路和方法

针对上述建立数学模型困难、求通解更难的问题，我们尝试另辟蹊径。考虑到我们的出发点是解决如何对空间探测雷达网生成欺骗航迹的这样一个工程问题，那么只要提出一种既能满足上述约束，又比较容易工程实现的干扰策略就是解决问题。也就是在求通解困难的情况下，求出问题的一个特解即可。

本文默认多部雷达为在同一平面内(或近似在一个平面内)。考虑一个满足条件的特解：若多干扰机所构成的多边形能与多雷达所构成的多边形平行且相似，则多雷达与对应干扰机的连线必然存在一个共同交点，该交点即为协同假目标点迹；若多干扰机在真空飞行过程中，该平行相似特性能一直保持，则多个协同假目标点迹会形成一条高逼真的假目标欺骗航迹。为简化起见，以3部干扰机协同干扰3部组网雷达为例。基于平行相似原理的欺骗航迹生成示意图如图1所示：在某一时刻，3部干扰机所构成的三角形与地面上的3部雷达构成的三角形平行且相似，那么3部雷达与对应的干扰机形成的3条射线在空间交于一点，即图中左侧的星号所示，也就是协同假目标点迹。在下一个时刻，干扰机组飞行到下一个位置，但构成的三角形依然与3部雷达构成的三角形平行且相似，同样可获得第2个空间协同假目标，也就是右侧星号所示。依次类推，一系列的星号点迹即可构成一条假目标欺骗航迹。

图1 基于平行相似原理的欺骗航迹生成示意图

从图1显然可以看出，如何在干扰机飞行过程中，使多部干扰机构成的多边形与雷达网构成的多边形一直保持平行且相似，这取决于各干扰机的弹道轨迹设计，是实现多机协同欺骗干扰的难点所在。对此，对干扰机飞行轨迹提出平行伴飞式、分导式两种策略。

平行伴飞式：从母舱释放出多部干扰机后，采用一定措施，使得某一时刻(记该时刻为初始时刻)，多干扰机的初始速度相同，而干扰机初始位置矢量差构成的多边形与多雷达构成的多边形平行且相似。根据“二体运动”方程，根据参考文献[18]中弹道中段轨迹的仿真生成方法，很容易仿真证明，在飞行过程中，多部干扰机速度仍然相同，其构成的多边形形状与大小不变，仍与雷达网构成的多边形保持平行相似(存在非常微小误差，可以忽略)。具体的证明过程不赘述。平行伴飞模式下多干扰机与雷达网的空间态势示意图如图2所示。

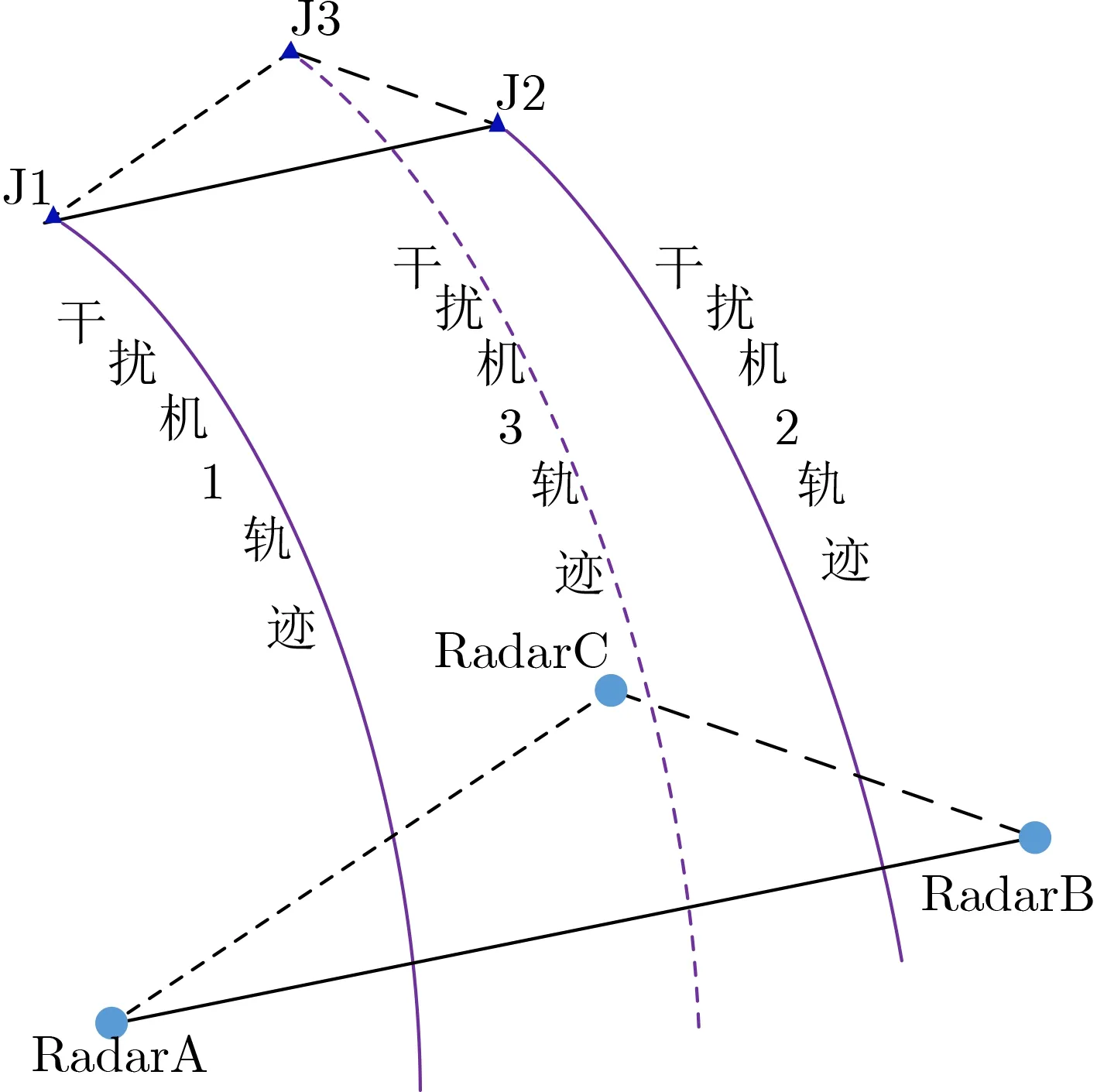
图2 平行伴飞式，多干扰机与雷达网空间态势示意图

分导式：同一时刻，母舱从同一位置抛射出多部干扰机，多干扰机的初始位置相同，则初始速度矢量差构成的多边形与多雷达构成的多边形平行且相似。同样容易仿真证明，在此初始条件下，在飞行过程中，多部干扰机构成的多边形不断放大，但仍能与雷达网构成的多边形保持平行相似(存在非常微小误差，可以忽略)。分导式多干扰机与雷达网的空间态势示意图如图3所示。

图3 分导式，多干扰机与雷达网空间态势示意图

从理论上讲，两种干扰机飞行策略都符合设计要求。但平行伴飞式要求干扰机从母舱释放后，需要在某一时刻到达需要的位置，构成一个特定的三角形，且飞行速度相同，水平方向相对速度为0。这可能要求设计必要的减速装置，在必要的时候为干扰机提供侧向加速度。因此平行伴飞式对母舱抛射要求较苛刻，工程实现难度高。因此，在后续研究中，从干扰机抛射工程易实现的角度出发，仅考虑分导式。

3 干扰实施方法

上一节给出了对空间探测雷达网高逼真多机协同航迹欺骗干扰的理论分析和思路方法，可见其关键技术是对干扰机初始运动状态的设计以及干扰机干扰延迟时间的计算。下面分别对这两项关键技术进行研究。

3.1 多干扰机初始运动状态设计

为简化起见，且不失一般性，以3部干扰机和3部雷达为例进行分析说明。如图4所示，不妨假定干扰机J1, J2, J3分别干扰雷达RadarA, RadarB,RadarC，3部干扰机所构成的三角形与3部雷达构成的三角形平行且相似。各干扰机与其对应的雷达连线的交点FT即为协同假目标位置。根据几何关系，它们满足：

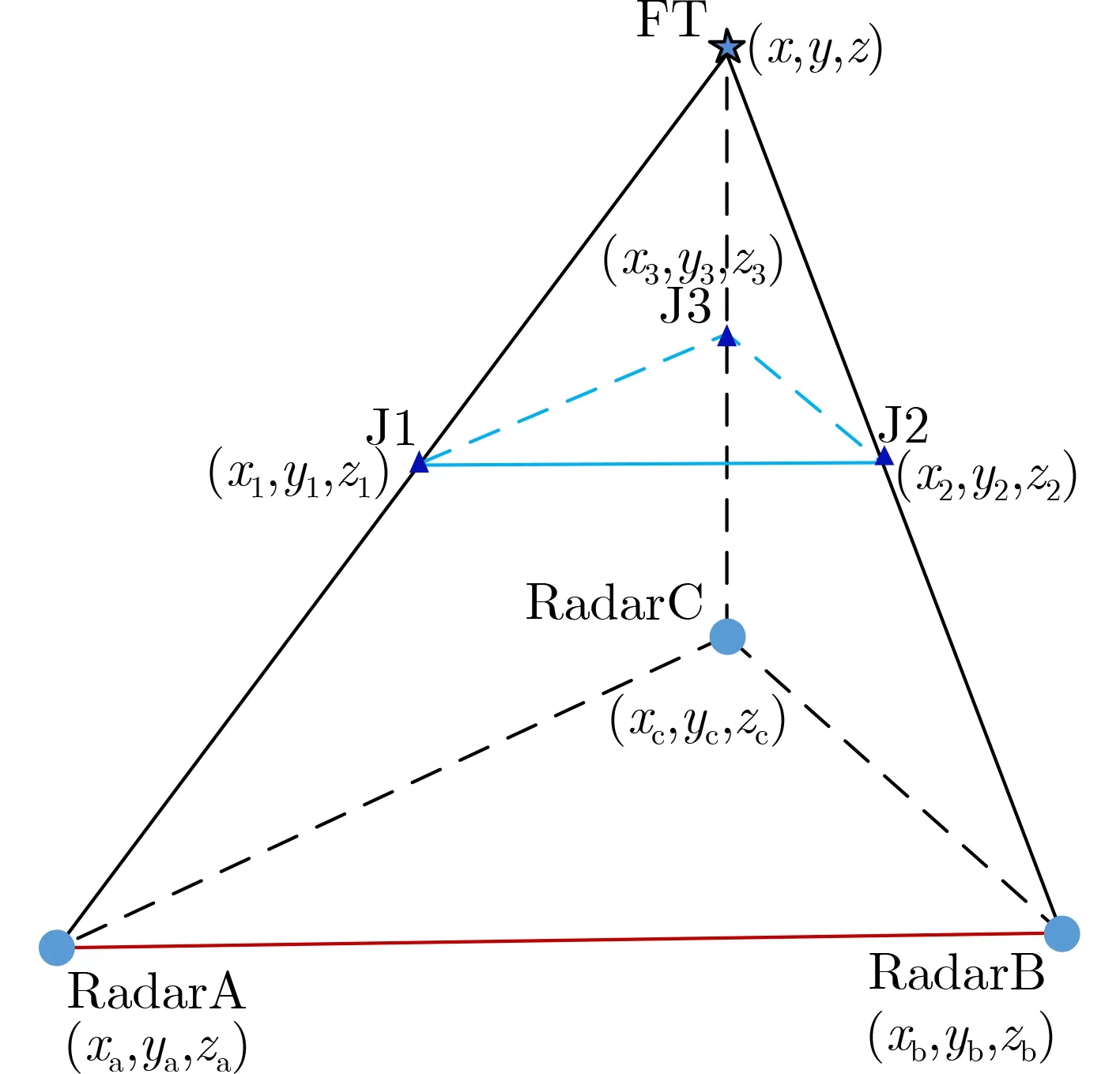
图4 3部雷达组网，协同假目标点迹示意图

3.2 多干扰机延迟时间设计

假定地球模型为椭球地球模型，参考ECI坐标系下弹道中段目标的轨道方程，则已知干扰机的初始运动参数，利用龙格库塔积分可计算每一时刻干扰机的运动参数，可获得干扰机1, 2, 3的运动轨迹，具体计算过程可参考文献[18]。

根据图4的几何关系，3条直线的交点即为协同假目标位置，据此列出方程组，解出假目标的位置。对于协同假目标FT，其坐标(x,y,z)满足式(6)方程

3.3 多机协同航迹欺骗干扰实施流程

解决了多干扰机初始运动状态和延迟时间的设计后，下面简要介绍对空间探测雷达网的高逼真多机协同航迹欺骗干扰设计及实施流程。首先进行干扰策略设计，即计算多个干扰机的初始位置、初始速度，以及干扰机的干扰转发延迟时间函数。在导弹发射之前，各干扰机统一时钟，以某个采样周期将干扰延迟时间离散化为一个干扰时间链表并装订入干扰机。当母舱飞行到某一位置时，将干扰机依照设计的初始速度抛射出来。当干扰机接收到雷达信号后，查询干扰时间链表，获取当前时刻干扰机所需的干扰延迟时间，然后按设定的干扰延迟时间复制转发脉冲。干扰机具体的工程技术实现及细节问题在本文不赘述。

4 仿真实验

在典型场景下对上述方法进行计算机仿真验证。假定地球为一标准匀质圆球，为简单起见，不考虑地球自旋。以3部干扰机协同欺骗干扰3部雷达组网为例。

地球模型为标准椭球，不影响问题本质且为简化起见，假定地球不自转。3部雷达布站位置为：雷达A(东经1.8°，北纬1°，高程0 m)，雷达B(东经2.5°，南纬1°，高程2 m)，雷达C(东经3.5°，北纬0.3°，高程5 m)。假定雷达距离测量标准差为3 m，方位角、俯仰角的测量标准差为1 mrad。3部干扰机在某一时刻(记为初始时刻)同时被母舱抛射出来，其初始速度差矢量所构成的三角形与3部雷达构成的三角形平行且形似。

仿真时间280 s，采样间隔为1 s。3部干扰机的空间距离如图5所示，3部雷达之间的速度差如图6所示。可以看出3部雷达随着时间的推进而越飞越开，但速度基本上保持不变的差距，这也符合我们的设计初衷。

图5 干扰机空间距离

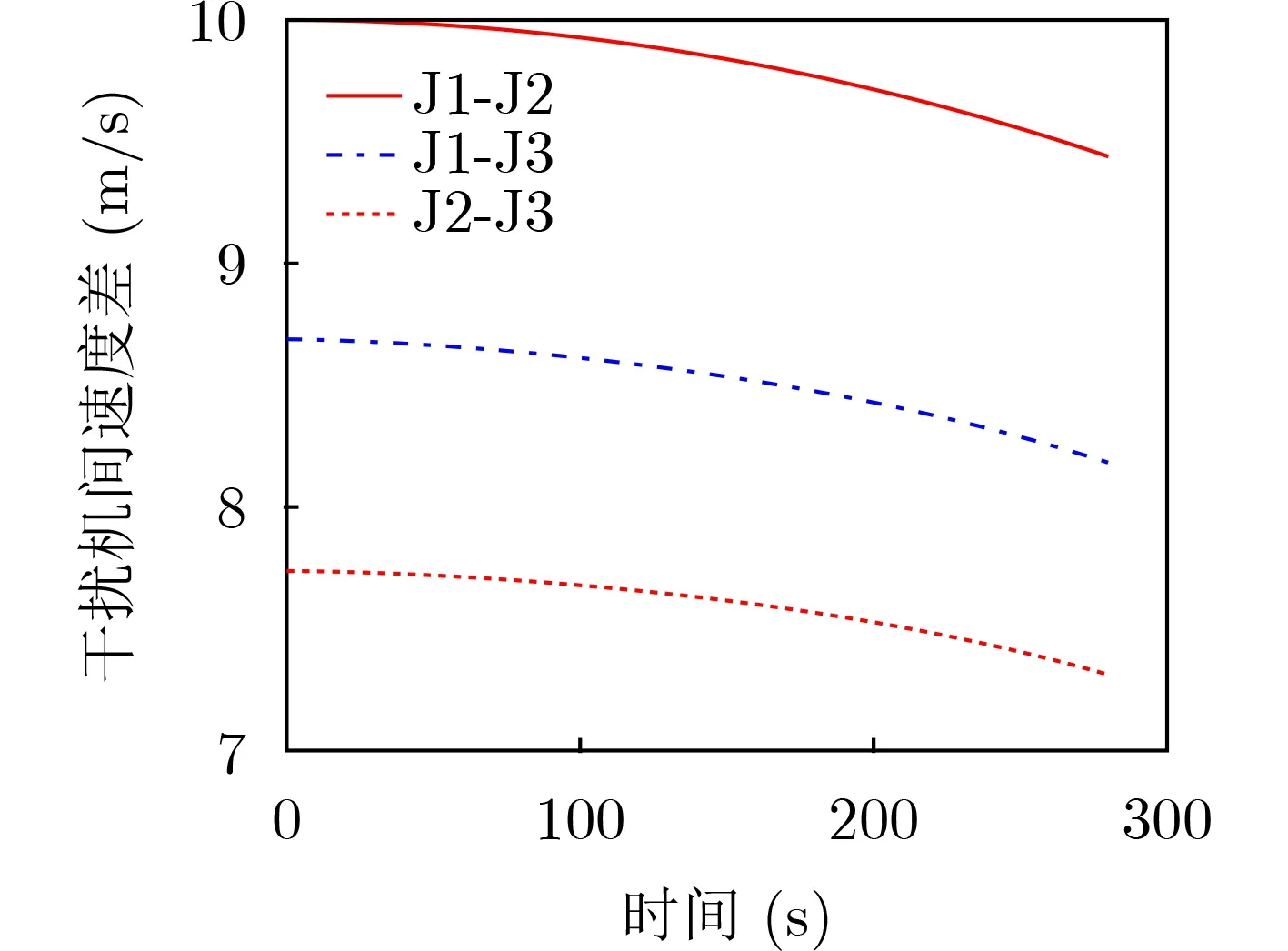
图6 3部干扰机的速度

设干扰机1，2相对于雷达A、雷达B产生的协同假目标为假目标1，干扰机1，3相对于雷达A、雷达C产生的协同假目标为假目标2，理论上假目标1，2应该在空间上是重合的，仿真计算了两个假目标的空间位置差，如图7所示，在280 s的飞行过程中，各个方向上的距离差最大不到0.5 m，这相对于几百公里的雷达观测距离是非常小的误差，基本上可以认为生成的协同假目标是凝聚在一起的。说明了该协同假目标生成方法是正确的。仿真计算为生成协同假目标3部干扰机所需要的延迟距离，对应的3部干扰机所需的转发延迟时间如图8所示。

图7 协同假目标空间位置误差

根据图8所示的3部干扰机延迟时间，实施分导式干扰策略，各部雷达对所观测到的真假目标信息进行滤波跟踪、关联处理，各部雷达站所得的航迹放在统一的一个坐标系下，共得到的12条航迹如图9所示。从图中可以看出，12条轨迹基本可以集合为4组。经过航迹关联融合处理后，剩下4条轨迹，如图10所示，其中3条实线轨迹分别对应干扰机1、干扰机2、干扰机3，其中1条虚线轨迹对应协同假目标航迹。这说明本方法可以成功地实现对于雷达组网的虚假航迹欺骗。为清晰显示可见，图9、图10仅截取了200～210 s的一段仿真航迹。

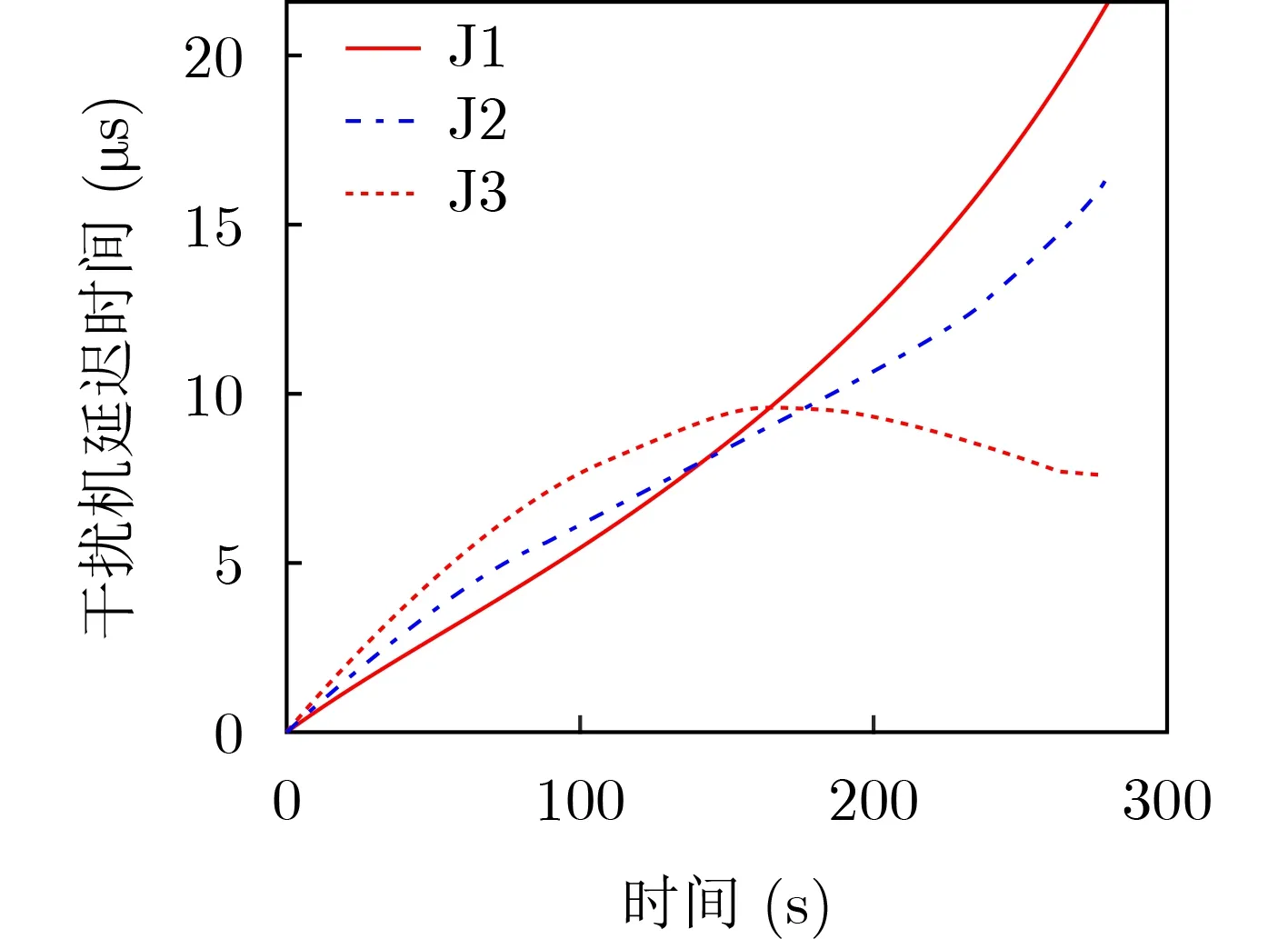
图8 干扰机延迟时间

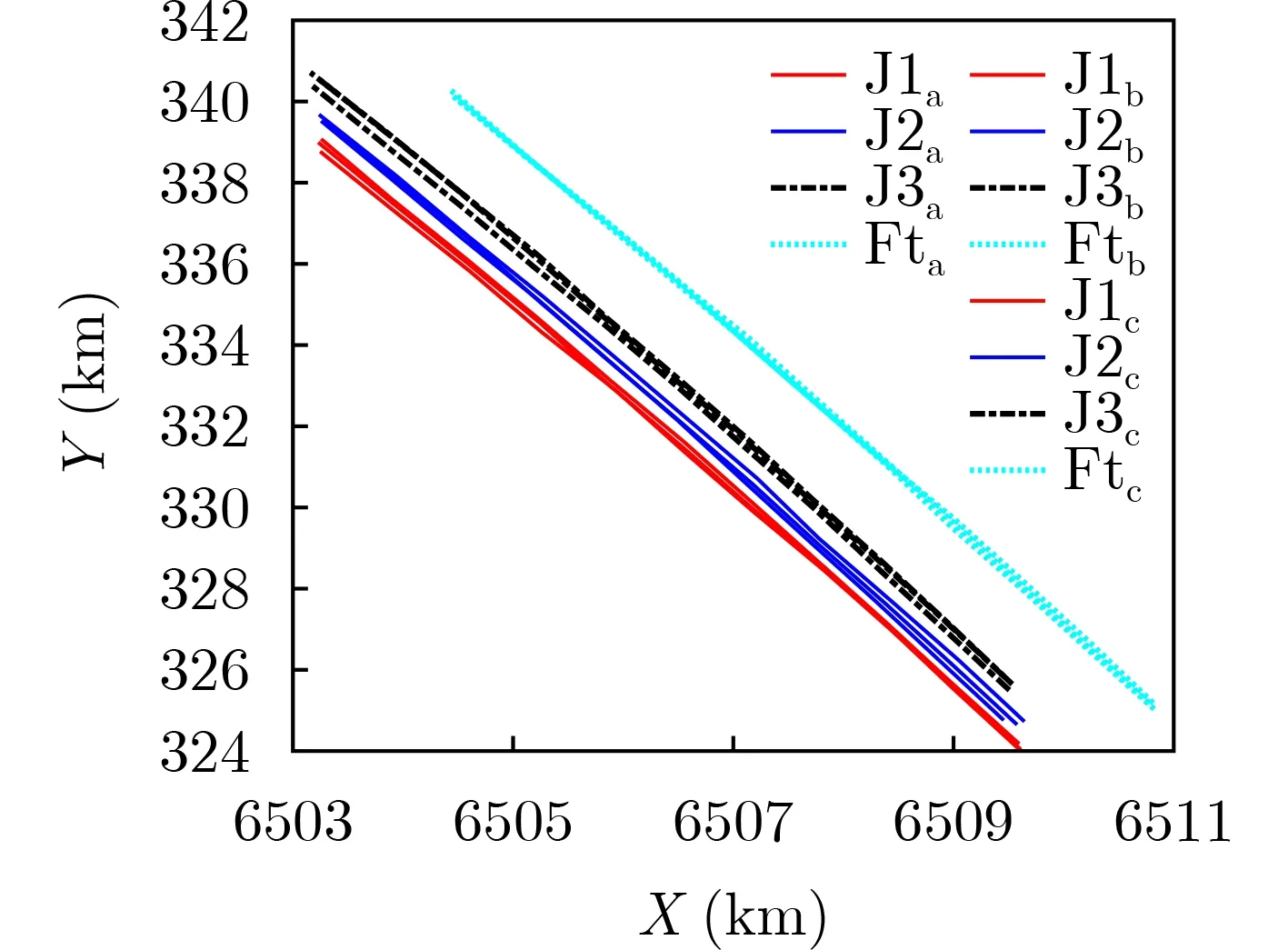
图9 统一坐标系下，3部雷达所观测到的12条航迹

图10 融合处理后的航迹

保持其他参数不变，依次改变仿真场景中的各种参数，如：雷达布站位置、第1部干扰机的初始运动状态、干扰机间的速度差矢量、雷达量测误差等，重复上述多部干扰机对多部雷达组网的协同欺骗干扰仿真实验，仿真结论不变：本文提出的欺骗干扰方法能成功形成持续稳定的、不会被融合中心识别的欺骗航迹。

5 结束语

本文提出了在自由飞行段使多干扰机保持构型、协同生成对空间探测雷达网的航迹欺骗干扰方法，解决了现有技术针对干扰机大气层外无动力飞行、难以对空间探测雷达网形成有效的多机协同航迹欺骗的难题。

本文提出的欺骗干扰方法的优点可总结如下：(1) 能对空间探测雷达网形成稳定持续的、不被融合中心识别的高逼真欺骗航迹；(2) 对干扰机要求不高：不需要干扰机载体具有动力及控制系统，不需要具有通信能力；(3) 干扰实施方案简单：只需要干扰机释放前装订好干扰时间链表，释放时按照计算好初始位置、初始速度即可，不需要后续过程控制。

文中提出的对空间探测雷达网高逼真多机协同航迹欺骗技术，涉及许多具体的技术细节问题，本文为了仅从原理上、方法上进行了关键技术的阐述，在许多方面没有详细展开说明，下面简要做些补充：

基于本文的干扰方法多部干扰机对多部雷达可以形成高逼真欺骗干扰航迹。实际上，由于雷达量测误差的存在，雷达网融合中心对来自多部雷达的航迹的关联和融合必然设定一定的门限，只要空间距离差小于关联门限的多条航迹就能被认为是一条航迹。也就是本文中设计的协同假目标航迹是理论上的“标称”欺骗航迹，在其附近的航迹仍可能被融合中心认为是真实航迹。以此“标称”欺骗航迹为基准，干扰机同时转发多个不同延迟的干扰脉冲(以理论计算出的干扰延迟时间为均值)，则在雷达网融合中心可以获得多条假目标欺骗航迹。这在理论上和工程上都是可行的，也可大大提高干扰机干扰效率。

文中以3部干扰机干扰3部组网雷达为例说明问题，实际上，该技术可以很容易地拓展到多部干扰机对3部雷达、多部干扰机对多部位于同一平面内的雷达网。而由于雷达雷达网融合中心的融合门限的客观存在，多部雷达也不需要严格在同一平面，只要在一定的容差范围内即可。

另外，关于本文方法对各种误差的适应性、欺骗航迹的逼真度和有效性、工程实用性等方面的问题，是下一步要研究的问题。