变电站轮式巡检机器人机械臂避障路径规划方法

李福鹏，曾红英，王 霞

(1.广东电网有限责任公司中山供电局，广东 中山 528400；2.浙江国自机器人技术股份有限公司，浙江 杭州 311422)

0 引言

站内设备巡检工作[1]作为确保变电站正常运行的关键环节，必须满足巡检规定频次，保证巡检工作量与质量，才能及时发现险情、消除故障，避免发生电力事故或事态升级。随着变电站无人化不断深入，人工智能技术、机器人技术迅猛进步，巡检机器人[2]日渐普及。

当前变电站常用的巡检机器人大都是以轮式架构为主的轮式机器人，此类型机器人集多种传感技术于一体，具有较高的灵活性与定位精度。为使此类机器人能够在特殊的变电站环境中灵活移动，顺利完成巡检任务，提出机械臂避障路径规划方法。针对该课题，近几年涌现出许多相对成熟的研究成果，薛阳等[3]提出改进人工势场法下双机械臂避障路径规划策略；曹毅等[4]提出改进双向快速扩展随机树下空间操作臂避障路径规划策略。

改进人工势场法需要依赖巡检环境的全部数据信息，而改进双向快速扩展随机树方法还未解决局部最优问题。故本文提出一种面向轮式巡检机器人的机械臂路径规化方法。

1 变电站轮式巡检机器人工作环境模型建立

变电站巡检环境在防止机器人机械臂发生碰撞的研究中有着重要作用。为合理规划避障路径，利用八叉树结构建模技术[5]，架构出轮式巡检机器人工作环境的三维模型。

将结构中每层的8个子节点作为当前分辨率下完全相同的8个像素块。假设传感器第c次的测量结果是kc，截止至第c次的传感估值是k1,c，φ(l)、φ(l|kc)、φ(l|k1,c)、φ(l|k1,c-1)分别为像素块l被占据的先验概率、第c次传感测量时被占据的概率、截止至第c次与第c-1次传感测量时被占据的概率，则像素块l被点云数据占据的判定条件式为

φ(l|k1,c)=

(1)

当像素块被点云数据占用时，划分该像素块为8个像素小块，以此类推，得到巡检环境的三维模型。利用式(2)更新模型，适应巡检环境变化，即

L(l|k1,c)=L(l|k1,c-1)+L(l|kc)

(2)

上式中的各项式分别为不同情况下像素块l被占据概率的对数变化。

2 轮式巡检机器人机械臂运动学

机械臂运动学是避障路径规划的基础，若想实现机械臂的复杂移动，就要采用数学模型来确定机械臂与环境关系。已知机械臂自由度n与连杆长度bw，连杆数量w=1,2,…,n，相对于基坐标系{0}的末端执行器坐标为(px,py)，将基坐标系{0}中的执行器坐标转换至世界坐标系{W}中的表达式为

(3)

(px,py){0}、(px,py){W}分别为基坐标系与世界坐标系下的执行器坐标；E为坐标的旋转变换矩阵。

根据坐标平移转换规律，坐标系变换矩阵为

T=rot(z,φ)trans(0,0,bω)trans(bw,0,0)rot(x,η)=

(4)

rot(z,φ)、rot(x,η)分别为坐标变换时连杆绕z轴转动φ、关节绕x轴转动η角度的旋转算子；trans(0,0,bω)、trans(bw,0,0)分别为坐标变换时关节与连杆各移动bω、bw距离的平移算子。

由此得到机械臂运动学模型的矩阵表达式为

(5)

ρx、ρy、ρz分别为机械臂在不同方向上的位置坐标；ϖ()、o()、μ()分别为关节在不同方向上因不同转角而形成的姿态。

当明确机械臂的期望末端位姿时，即

(6)

Tn为齐次变换矩阵。

(7)

3 变电站轮式巡检机器人机械臂避障路径规划

轮式机器人机械臂在执行巡检任务过程中，各关节的旋转移动行为均有可能使连杆碰撞到障碍物。故依据机械臂运动学模型得到各关节对应位姿，确定关节三维坐标，以此来防止机械臂连杆碰撞障碍物。

假定机械臂连杆AB两关节的三维坐标分别为(xA,yA,zA)、(xB,yB,zB)，则描述该连杆圆柱体的中心线的表达式为

(8)

α、β、γ分别为3个轴向的相关系数，取任意常数；(x′,y′,z′)为连杆圆柱体中心线上任意一点。

(9)

(10)

由此得出中心O与连杆AB间距最小值dminO-AB。

基于连杆不碰撞障碍物的必要条件，采用下列六次多项函数式，获得各关节的角速度与角加速度连续轨迹即

ψt=a0+a1t+…+an-1tn-1+Ktn

(11)

ψt为t时刻各关节的角度；ai为待定系数，i=0,1,…,n-1；K为非固定参数，就n自由度来说，也是一个n维向量，K=[K1,K2,…,Kn]，用于调整机械臂的移动轨迹，在确保成功避障的同时优化路径。

为使巡检机器人的机械臂能始终在避障路径上保持平稳的不间断运行，利用贝塞尔曲线[8]处理规划的避障路径，令锯齿与突变现象更加平滑。假设贝塞尔曲线上有m+1个控制点，则采用下列m次多项式界定该曲线形式，即

(12)

m为贝塞尔曲线阶数；Qj为第j个控制点的坐标值，j=0,1,…,m；u为曲线函数，取值在0到1之间；Vj,m(u)为伯恩斯坦多项式[9]。

扩展曲线多项式(12)，得出曲线参数方程为

S(u)=Q0u0(1-u)m+mQ1u(1-u)m-1+…+

mQjuj(1-u)m-j+…+Qmum

(13)

通过各点坐标，即可得到贝塞尔曲线[10-11]。其中，Q0、Qm分别为曲线的起始点与结束点，其他节点均为控制点。

因贝塞尔曲线两端点满足S(0)=Q0、S(1)=Qm，故用曲线的2个端点联立出方程组，描述所规划的避障路径，令曲线起始点Q0即路径起点(xs,ys,zs)，结束点Qm即路径终点(xg,yg,zg)。经贝塞尔曲线不断处理各关节的移动轨迹，提升整个避障路径的平滑程度，即

(14)

4 变电站巡检机器人机械臂避障路径规划仿真试验

4.1 试验平台搭建

选取TR20型号的变电站轮式智能巡检机器人作为试验对象，机械臂是型号为Universal UR系列的六自由度关节型装置，Denavit-Hartenberg参数如表1所示。

表1 轮式巡检机器人机械臂Denavit-Hartenberg参数

采用SolidWorks软件建立该机械臂的三维模型。根据表1中的Denavit-Hartenberg参数，选用simulation仿真工具，模拟机械臂末端执行器的避障路径轨迹。选取改进人工势场法与改进双向快速扩展随机树2种避障路径规划策略展开对比仿真试验，以凸显本文方法的优越性与实践性。

4.2 机械臂避障路径规划的轨迹分析

利用robot studio工具绘制出机械臂末端执行器在3种方法各自规划的避障路径上的运行轨迹，并将其与期望路径作对比。机械臂末端在三维空间中的运行轨迹如图1所示。

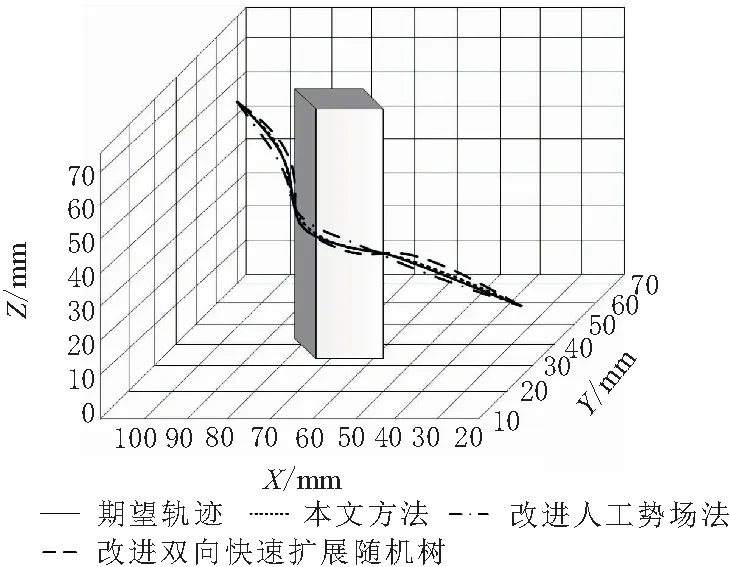
图1 各方法规划的机械臂避障路径

由图1可知，3种方法均能有效规划出无碰撞路径；对比方法规划的路径在整体方向上与期望路径一致，但改进双向快速扩展随机树规划法因局部最优问题，导致轨迹偏离点较多且误差较大，最大误差为3.2 mm，改进人工势场法次之，最大误差为2.4 mm；而本文方法的避障路径则与期望路径之间存在较小误差，最大值仅有1.1 mm，该误差产生的主要原因是计算过程中的小数点保留精度问题。

该试验环节结果表明，本文方法利用八叉树结构建模技术架构的巡检环境三维模型，为合理规划避障路径提供了可靠依据，通过不断更新三维模型，令机械臂更好地适应环境变化，故规划的避障路径不仅使机械臂始终未与障碍物发生刮碰，而且精度更优越，更理想地实现了躲避障碍物的目的。

4.3 机械臂避障路径规划效果量化分析

为直观地说明本文方法的性能优势，分别从路径距离、规划时间2方面比较、分析3种方法规划的多组避障路径指标数据。仿真试验结果如图2所示。

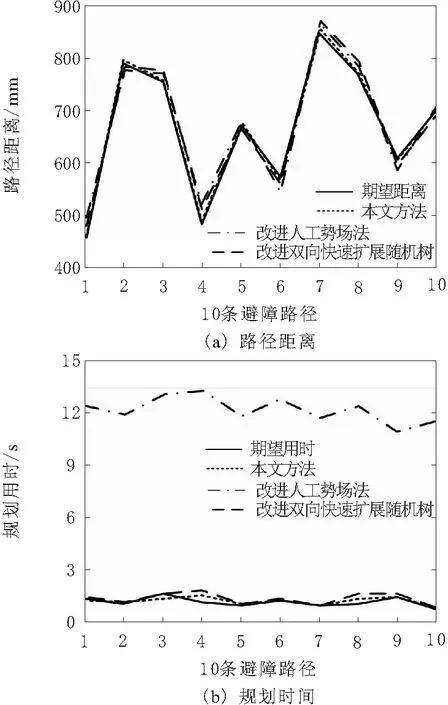
图2 各方法避障路径规划指标

由图2可知，各方法规划的避障路径距离相差无几，均有较好表现，比较期望路径距离，本文方法相对更优；对于规划速度而言，改进双向快速扩展随机树规划法滤除了冗余节点，故避障路径的规划用时平均不超过2 s；本文方法根据运动学模型确定的机械臂与环境关系，设立避障必要条件，得到关节角速度、角加速度的连续轨迹，不仅大幅缩短了避障路径的规划用时，使规划速度比改进双向快速扩展随机树规划法更快，并显著优于改进人工势场法，甚至在规划第1条、第3条和第9条路径时，略快于期望用时。

路径总长与规划时间2项指标数据足以表明，本文方法的综合性能更加优越，更能满足变电站巡检的合理性与实时性需求。

5 结束语

变电站环境特殊，为保证机器人安全作业，巡检工作顺利进行，提出了一种机械臂避障路径规划方法。经试验表明，该方法可防止机器人在巡检过程中与电力设备等物体发生碰撞，引发故障、事故。