考虑外部扰动的四轮移动机器人运动轨迹控制优化方法

2023-03-01纪永

机械与电子 2023年2期

纪永

(上海城建职业学院，上海 201415)

0 引言

人们在生活中对移动机器人的需求随着经济的发展不断提高[1]。在军事、航天和工业等领域中，移动机器人具有重要作用，送餐机器人、平衡车和扫地机器人是市场中的主要应用机器人，其大部分都为非全向移动机器人，这类机器人的运动控制器和路径规划算法只适用于简单的环境[2-3]。四轮移动机器人应用广泛，灵活性较高，可以满足人们的需求。对四轮移动机器人运动轨迹实行控制优化可以提高用户的体验感以及机器人的实用性。

黄健萌等[4]首先确定了控制优化目标，优化机器人的路径序列，在JPS搜索规则的基础上获取多条移动机器人路径，平滑处理上述获取的路径，通过多段高阶多项式完成移动机器人运动轨迹的控制优化，该方法获得的运动轨迹与期望轨迹之间存在较大误差，存在轨迹控制效果差的问题。陈素霞等[5]将自适应控制算法应用到轨迹控制中，将跟踪误差作为控制优化的目标，根据机器人运动模型设计Lyapunov函数，结合上述函数通过backstepping方法设计机器人运动轨迹控制器，该方法控制结果的距离误差较大。贾松敏等[6]在机器人运动轨迹控制优化过程中引入反步控制技术，构建机器人运动学模型，结合自抗扰技术构建运动轨迹控制器，实现轨迹的优化控制，该方法无法精准地控制机器人的角速度，导致机器人运动的稳定性较低。

为了解决上述方法中存在的问题，提出考虑外部扰动的四轮移动机器人运动轨迹控制优化方法。

1 四轮移动机器人数学模型

1.1 运动学模型

设ϑ=ϑr=ϑw为运动过程中相应的方位角，Ow-XwYw为基准坐标系[7-8]，Or-XrYr为相对坐标系，具体位姿分别为(xw,yw,ϑw)、(xr,yr,ϑr)，轮胎线速度为vi，i=1、2、3、4，即

(1)

基准坐标系和相对坐标系之间的关系为

(2)

结合上述公式，获得机器人在运动过程中的4个轮胎线速度为

(3)

1.2 动力学模型

设gi为电机在机器人4个轮上的驱动力，Y1为平移运动时机器人产生的动能，Y2为旋转运动时机器人产生的动能，Y3为电机旋转过程中机器人产生的动能，其计算公式分别为

(4)

机器人在移动过程中产生的能量损失R为

(5)

Fm为黏性摩擦因数；Fa为地面与机器人底座之间存在的摩擦因数。

分析机器人电机的特性，获得其运动过程中产生的驱动力gi，综上所述，本文方法构建的机器人动力学模型[9-10]为

(6)

2 机器人运动轨迹控制优化

2.1 路径轨迹规划

本文方法采用人工势场法[11-12]规划机器人的运动轨迹。设置正比例系数satt，建立引力势场函数Iatt(S)为

Iatt(S)=fc(s,sgoal)satt

(7)

fc(s,sgoal)为目标点与机器人质点之间存在的距离。

通过上述函数获得吸引力Gatt(s)为

Gatt(s)=-∇Iatt(S)

(8)

设置正比例系数srep，用Irep(s)表示障碍物在环境中产生的斥力，当最短距离f(s,sobs)小于f0时会产生斥力势场Grep(s)，四轮移动机器人在斥力势场的影响下会躲开障碍物，即

mRG为机器人产生的单位向量；mOR为障碍物点的单位向量。

在上述结果的基础上，四轮移动机器人的合力Gtotal(s)为

Gtotal(s)=Gall(s)+Grep(s)

(10)

四轮移动机器人在合力Gtotal(s)的作用下向目标点移动，获得移动方向和移动轨迹，实现四轮移动机器人运动轨迹的规划。

2.2 机器人运动轨迹控制器

考虑外部扰动和不确定性的影响，设Mt为等效正定惯性矩阵，将未知干扰参量R(t)引入机器人动力学模型中，即有

(11)

T为等效力矩；C为向心力矩阵。

机器人在静止坐标系中的移动轨迹可通过光滑曲线q(t)=[X(t),Y(t),θ(t)]T描述，用qd(t)=[X(t),Y(t),θ(t)]T表示运动过程中的期望轨迹，则机器人运动轨迹控制优化过程中的轨迹跟踪误差e(t)为

e(t)=qd(t)-q(t)

(12)

本文方法在滑膜控制基本原理[13-14]的基础上，选取线性滑膜面作为四轮移动机器人的滑膜面d(t)，低通滤波器W(s)的表达式为

W(s)=μi/(di+μi)

(13)

在四轮移动机器人动力学模型的基础上得到

(14)

u为滑膜控制器的输出。

分析滑膜控制的基本理论，设计机器人运动轨迹控制器J的滑膜控制规律为

(15)

ιsgn(s)为切换函数；J0为机器人运动轨迹控制器J的精确值。

假设各参数在机器人运动轨迹控制器J0是已知的，但由于外部扰动和不确定性等影响因素，导致参数在控制器中势场发生变化。为了解决上述方法中存在的问题，可通过自适应控制方法[15]减少运动轨迹控制器受参数的影响程度。

(16)

通过上述分析，重新设计四轮移动机器人在运动过程中的滑膜控制率为

(17)

本文设计的运动轨迹控制器结构如图1所示。

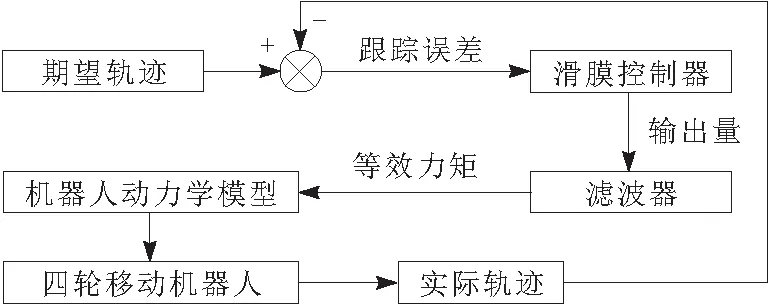
图1 运动轨迹控制器

3 实验与分析

为了验证考虑外部扰动的四轮移动机器人运动轨迹控制优化方法的整体有效性，进行如下测试。

采用本文方法与不同方法的运动轨迹进行比较，结果如图2所示。

图2 不同方法的运动轨迹控制结果

由图2可知，采用本文方法控制四轮移动机器人运动时，获得的运动轨迹与期望轨迹基本相符，可准确地完成四轮移动机器人运动轨迹的控制。

在上述测试环境中，采用本文方法、文献[3]方法和文献[4]方法控制四轮移动机器人，对比不同方法的y轴距离误差、x轴距离误差，获得相应的距离误差响应曲线，结果如图3所示。

由图3a可知，对比3种方法的测试结果，本文方法控制机器人运动轨迹时，可在较短时间内将x轴误差降低为0.2 m。

由图3b可知，与x轴距离误差相比，本文方法获得y轴距离误差所用的时间相对较少，在10 s时就可将y轴距离误差控制为0.2 m。

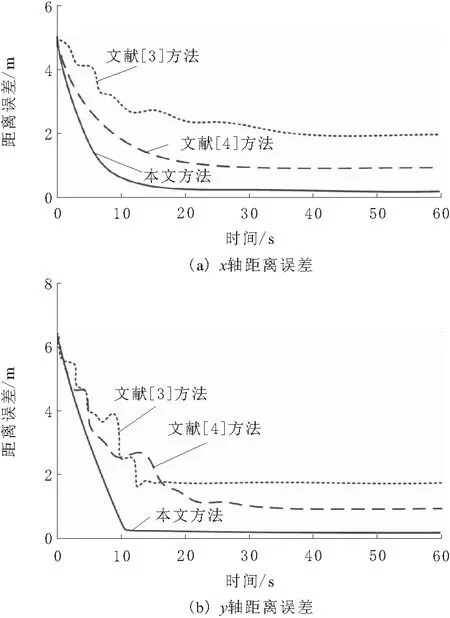
图3 不同方法的距离误差

角速度误差是控制四轮移动机器人运动轨迹的关键，在实验开始之前，设定四轮移动机器人运动期望角速度，采用本文方法、文献[3]方法和文献[4]方法控制四轮移动机器人的角速度，将控制结果与期望角速度对比，角速度误差越小，表明方法的控制效果越好，反之，方法的控制效果越差。

将控制周期设定为1 min，采用本文方法、文献

[3]方法和文献[4]方法在相同环境中控制四轮移动机器人做运动，获得3种算法的角速度误差曲线，如图4所示。

图4 不同方法的角速度误差

由图4可知，采用本文方法测试时，获得的角速度误差曲线前期存在小波动，在15 s处角速度保持为0，直至实验结束；采用文献[3]方法测试时，角速度曲线在前30 s内存在波动；采用文献[4]方法测试时，获得的角速度误差曲线波动最大，且曲线平稳所用的时间高于本文方法和文献[3]方法。通过上述测试可知，本文方法可精准控制四轮移动机器人的角速度，且控制波动小，因为本文方法设计运动轨迹控制器时，利用自适应控制方法避免四轮移动机器人受外部扰动和不确定性等影响因素的干扰，避免机器人在运动过程中出现抖动，提高了方法的控制稳定性。