一种基于生态流量的水资源开发利用率阈值估算方法

张晓璐，刘德地

（武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072）

0 引 言

水资源开发利用率阈值是进行水资源开发利用、安全评价、风险调控与综合管理的控制性指标，国际上常以年取水量与年可获得水资源量的比值作为水资源开发利用率，取40%作为其阈值，并以此为依据判断一个区域水资源利用状况是否处于安全或者高压力状态［1］，但随着该阈值在水资源管理科学研究与实践中的广泛应用，其确定依据和合理性越来越受到人们的高度关注。Balcerski［2］最早定义了水资源利用指数为年可获得水资源量与年取水量的比值，并认为其小于5时，水资源开始限制经济发展。1972年Szesztay［3］首次在实际中应用Balcerski的方法分析了欧洲30 个国家的水资源利用状况，1976年Falkenmark and Lindh［4］将水资源开发利用率定义为水资源利用指数的倒数，进一步解释了在欧洲当水资源开发利用率超过20%时，水资源的进一步开发将会增大必要的基础设施工程投入，从而影响国家的经济发展。1993年Kulshreshtha［5］根据当时的用水情况预测了在气候变化情境下世界上各个研究区域的水资源开发利用率，提到在未来日本的水资源开发利用率将保持在40%以下，这相对亚洲其他国家是较不脆弱的。1997年Raskin［6］将水资源开发利用率分为4 个等级，将40%设定为水资源高压力阈值，并在全球范围内评价了各个区域从1995年到2025年间水资源压力状态的变化，但并未明确给出40%阈值的确定依据和参考文献。Hanasaki等［7］也认为水资源开发利用率阈值为40%的来源和科学依据不明，然而自Raskin［6］水资源状况的研究报告发布后，大量有关水资源安全、水资源压力的评价报告和论文均以40%作为水资源安全指标的阈值［1，8-12］。我国众多研究者对水资源开发利用率有着不同的定义和计算，王建生［13］提出地表水资源可利用量和水资源可利用总量的计算方法，对我国各水资源一级区和全国水资源可利用率进行了计算和分析。祝晓宇［14］等则基于水资源调入调出关系，分析了我国各水资源一级区地表水资源开发利用率及其变化趋势。左其亭［15］评述了现有水资源利用率的概念和计算公式，认为现有的水资源利用率概念不清，并提出了扣除非供人类使用的生态需水等后计算的净水资源利用率的概念和计算公式。马涛等［16］总结了非常规水资源的现状开发利用量和开发利用模式并分析了其中存在的主要问题，提出了针对性对策以更好地支撑非常规水资源开发利用管理和实践来缓解水资源危机。李丽娟和郑红星［17］认为海、滦河流域出现生态问题的根本原因是水资源的过度开发，应考虑河流的基本生态环境需水量来帮助把握水资源开发利用的程度。王西琴和张远［18］从水质和水量综合角度探讨了水资源开发利用率阈值，在同时考虑水资源消耗系数、污径比和生态流量的前提下，给出了我国七大流域水资源利用率阈值。刘晓燕等［19］通过耦合分析黄河的输沙需水及不同鱼类和湿地对生态需水和流量的要求，并考虑水库群难以调蓄的洪水，对黄河未来可供人类利用水量进行了预测，说明了水资源开发利用阈值具有动态性特征。还有一些研究者［20-25］从水足迹视角分析了当前水资源利用结构特征，从考虑生态用水的角度下综合评价了我国不同省市或流域的水资源可持续利用情况，为接下来各流域城市制定和调整水资源可持续开发利用管理政策提供了新方向。

目前结合生态对水资源开发利用率的研究常根据生态流量利用比例进行估算，其中的生态流量法采用Tennant法［26］，如贾绍凤和柳文华［27］认为Tennant法中河流保有60%的多年平均年径流量可以保障河流大多数生物生长是河流水资源开发利用率不超过40%的合理依据，而Tennant 法存在以下不足：①采用多年平均年径流量的百分比表示生态流量，没有考虑其逐月或年际变化；②采用多年平均月径流量的百分比表示生态流量的改进Tennant 法，未能克服极端年际流量的影响；③不同流域或同个流域不同河段都采用同一个生态流量百分比，未考虑不同流域或不同河段间的差异性。针对Tennant 法的不足，本文在应用SWAT 模型模拟径流，得到反映时空分布的各子流域径流的基础上，通过基于多层次生境条件的改进Tennant法（Modified Tennant Method based on Multilevel Habitat Conditions，MTMMHC 法）［28，29］计算各月份在丰、平、枯年份的各级生态流量，进一步根据河道内水量平衡原理，建立水资源开发利用率阈值与河道内生态流量的互补关系，将河道内水量计算问题转化为河道出口断面流量的监测问题，通过保证子流域出口的生态流量来确保整个子流域的水资源开发符合要求。考虑到目前较难做到实时监测和反馈，仅使用平均流量来计算，最终得到各子流域（表征不同河段）各月份在不同水平年的各级水资源开发利用率阈值，研究路线见图1。MTMMHC 法充分考虑了流量的年内和年际变化以及极端年际流量与流量年内分布不均的影响，最终结果改进了水资源开发利用率阈值在不同水平年和河段为单一值的情况，体现了其时间和空间变异性，可为水资源综合开发利用管理及调水工程的运行管理提供支撑。

图1 基于生态流量的水资源开发利用率阈值研究路线图Fig.1 Research roadmap of water exploitation index based on ecological flow

1 研究方法

1.1 SWAT分布式水文模型

SWAT模型是美国农业部和农业研究局开发的流域尺度的分布式水文模型。在SWAT模型中每一个水文响应单元均涉及截留、融雪、地表径流、壤中流、地下径流和蒸散发等［30］（图2），地表径流量的计算主要采用SCS 径流曲线数法［31］和Green &Ampt 下渗法［32］，本文选用SCS 径流曲线数法，壤中流采用动力储水模型计算，地下径流只有浅层地下水对该流域的河川径流有补给时才产流，蒸散发的计算主要采用Penman-Monteith法［33］、Priestley-Taylor 法［34］和Hargreaves 法［35］，本文选用Penman-Monteith法；河道汇流演算方法采用Muskingum法［36］。

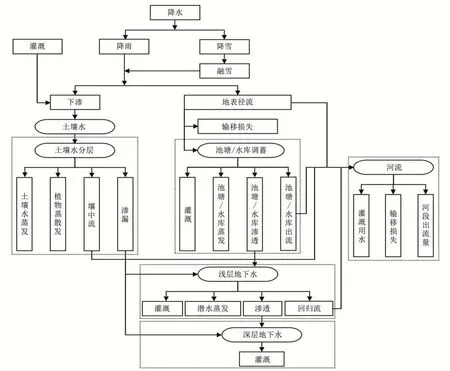
图2 SWAT模型结构示意图Fig.2 Schematic diagram of SWAT model structure

1.2 MTMMHC法计算生态流量

生态流量采用MTMMHC 法计算，其主要优势在于：①同传统Tennant 法以平均流量的单一百分比作为生态流量不同，通过它可以计算出不同月份不同水平年的生态流量，其中水平年的划分基于月平均流量序列的不同保证率，能充分考虑流量的年内变化和年际变化（时间变异性）；②它以不同水平年组不同月份的月中值流量代替Tennant 法中年平均流量或月平均流量，考虑了极端年际流量及流量年内分布不均的影响（时间变异性）；③采用MTMMHC 法计算流域内不同子流域的各级生态流量，即在不同河段采用不同的生态流量，能改进在整个流域采用同一个生态流量的情况（空间变异性）。

MTMMHC 法采用逐月流量历时曲线（Flow Duration Curve，FDC）改进法［29，37］计算最小生态流量（Minimum Ecological Flow，MEF）即生态基流，考虑了MEF的年际变化和逐月变化。其主要步骤是：首先，根据月平均流量的保证率P对各月的日流量系列划分丰（P＜25%）、平（25%＜P＜75%）和枯（P＞75%）水平年组；其次，使用各个月份在不同水平年组的日均流量构建逐月FDC；最后，取90%历时点流量Q90和95%历时点流量Q95的平均值作为各个月份在不同水平年的MEF：

式中：i=1，2，3，分别为丰、平、枯水平年；j=1，2，…，12，分别为1-12月；MEF（ij）为第i水平年第j月份的最小生态流量，m³∕s；Q90（ij）为第i水平年第j月份FDC 上的90%历时点流量，m³∕s；Q95（ij）为第i水平年第j月份FDC上的95%历时点流量，m³∕s。

MTMMHC 法以50%历时点流量Q50代替Tennant 法中多年平均年径流量（Average Annual Flow，AAF），即为最优生态流量（Optimum Ecological Flow，OEF）的上限：

式中：OEFmax（ij）为第i水平年第j月份最优生态流量上限，m³∕s；Q50（ij）为第i水平年第j月份FDC上的50%历时点流量，m³∕s。

基于Tennant 法的等差数列分级思想，MTMMHC 法将MEF（ij）～OEFmax（ij）初步等分为10级，将第6级设定为最优生态流量的下限即最适宜生态流量：

式中：OEFmin（ij）为第i水平年第j月份最优生态流量下限，m³∕s。

MTMMHC 法以10%Q50代替Tennant 法中10%AAF作为MEF（ij）～OEFmin（ij）各级的等差以优化其分级数量，OEFmin（ij）～OEFmax（ij）不再分级，即初步等分后的6～10 级仅保留了OEFmin（ij）和OEFmax（ij），生态流量总分级数最大为7，那么MEF（ij）～OEFmin（ij）（包括两端点）分级数最大为6。各子流域MEF（ij）～OEFmin（ij）的分级数为MEF（ij）～OEFmin（ij）分级数nij的平均值，为方便计算，最终取各子流域MEF（ij）～OEFmin（ij）分级数的众数作为所有子流域MEF（ij）～OEFmin（ij）分级数N：

式中：N为所有子流域MEF（ij）～OEFmin（ij）的分级数，N≤6（MEF（ij）～OEFmin（ij）分级数最大值为6）；nij为第i水平年第j月份MEF（ij）～OEFmin（ij）的分级数；Mode（·）为求众数函数；Average（·）为求平均值函数；Round（·）为四舍五入函数。

最终MEF（ij）～OEFmin（ij）间各级生态流量为：

式中：Em（ij）为第i水平年第j月份第m级生态流量，m³∕s，m=1，2，…，N-1。

1.3 水资源开发利用率阈值估算

生态需水（Ecological Water Requirements，EWRs）是维持河道生态系统平衡的基本水量，也就是河道生态系统在不同时间尺度上的需水总量，其计算公式如下：

式中：Qall为河道总水量，m³；Ea为河道生态流量占比，即不同时间尺度生态流量占其多年平均同期径流的比值，本文取其为各月份在不同水平年的各级生态流量占各水平年组多年平均月径流量（Average Monthly Flow，AMF）的比值。

生态用水（Ecological Water Use，EWU）指生态系统维持一定的稳定状态时实际所利用的水量［38］，可以理解为在一定开发和消耗水平下剩余在河道内供其维持生态平衡的水量，其计算公式如下：

式中：u为水资源开发利用率；k为水资源消耗系数。

根据河道内水量平衡原理，当EWRs=EWU时，河道生态系统处于适宜状态；当EWRs＜EWU时，河道内水量不仅能维持当前河段内河道生态系统平衡，还有富余的水分；当EWRs＞EWU时，河道内水量不足以维持河道生态系统的正常功能，出现生态缺水［38］。

因此，要保证河流生态系统不受破坏，需要满足：

即：

从而得到，水资源开发利用率：

故水资源开发利用率阈值为：

若在跨流域调水河流或流域内调水河段，调出的水不会回到原流域或河段或在某一断面取水，回归水不能回归到当前河段，而是排放到其他河段或只考虑水资源一次利用，而不考虑或无法考虑其多次利用时，取水量与耗水量相等，即水资源消耗系数k取为1，则水资源开发利用率阈值为：

式（12）为水资源开发利用率阈值与河道内生态流量之间的互补关系，其实质为河道内生态用水与河道外社会经济活动用水的相互耦合，反映了生态用水的动态性特征，实现了从单一考虑水资源开发利用对经济社会发展的工程影响［2-4］（如最早的水资源开发利用率阈值为20%）和考虑固定比例生态流量对水资源开发利用的影响［27］（如水资源开发利用率阈值为40%），到考虑动态生态环境需水对水资源开发利用影响的转变，但水资源开发利用率阈值还需综合考虑水资源系统中供水子系统、水力发电子系统和水生态环境保护系统之间相互转换的纽带关系等，如还可从水资源系统回弹性角度进行估算。

2 研究区域概况与数据

2.1 汉江流域概况

汉江是长江第一大支流，其干流发源于陕西省秦岭南麓，干流流经陕西、湖北两省，在武汉汇入长江，干流全长1 577 km，流域水系呈现叶脉状，支流众多，流域跨度大，面积达15.9 万km2。汉江流域属亚热带季风区，气候温和湿润，降水量丰沛，水资源总量非常丰富，但降水年内分配不均，主要集中在夏季，暴雨多发生于7-10月［39］，径流年际变化大，多集中在5-10月［40］。汉江流域是我国重要的战略水源地，随着“南水北调”中线、“引汉济渭”、兴隆水利枢纽、“引江济汉”、“鄂水北调”等工程的实施，汉江流域和调水工程受水区的水资源系统、生态环境均发生了改变［41］。作为诸多水资源工程的水源地，汉江流域有着沉重的水资源负担，不同河段不同季节水资源开发利用率阈值的研究能够为其工程规划提供合理的参考，有助于维持其河流生态系统平衡。

2.2 数据收集与处理

2.2.1 气象数据

汉江流域气象数据来源于中国国家气象局，选取了汉江流域13 个国家气象站点［图3（a）］1980-2000年所测得的逐日气象数据资料（包括降水量、最低最高气温等），用于驱动SWAT水文模型进行径流模拟。

2.2.2 径流数据

观测径流数据来源于长江委水文局，选取了汉江干流上包括白河（32.82°N，110.12°E）、黄家港（32.52°N，111.52°E）、襄阳（32.03°N，112.17°E）和皇庄（31.19°N，112.56°E）4 个水文站［图3（a）］作为干流主要测站，径流数据包括这4 个站点1980-2000年的逐日平均径流量。

2.2.3 数字高程模型（Digital Elevation Model，DEM）

DEM 数据［图3（b）］来源于中国科学院地理科学与资源研究所资源环境科学与数据中心，数据分辨率为1 km，需对DEM原始数据进行拼接、裁剪和填洼等处理。

图3 汉江流域SWAT模型输入数据Fig.3 Input data of SWAT model in Hanjiang River basin

2.2.4 土地利用/覆被数据（Land-Use and Land-Cover，LUC）

LUC 数据来源于中国科学院地理科学与资源研究所资源环境科学与数据中心，采用2015年空间分辨率为1 km 的栅格数据。LUC 类型包括耕地、林地、草地、水域、居民地和未利用土地6 个一级类型以及水田、旱地、有林地和灌木林等25 个二级类型。根据SWAT 模型中LUC 分类标准进行重新分类，最终获得7种LUC类型［图3（c）］。

2.2.5 土壤数据

土壤数据来源于联合国粮农组织和维也纳国际应用系统研究所构建的世界土壤数据库（Harmonized World Soil Database，HWSD），数据分辨率为1 km。经美国华盛顿州立大学开发的土壤水特性软件SPAW 中的土壤水分特征（Soil-Water-Characteristics，SWCT）参数估计模块计算出研究区域内所含土壤的有关物理参数，结合SWAT 模型的土壤类型划分标准，将研究区内物理特性相近的土壤类型归为同一类型，最终得到11种土壤类型［图3（d）］。

3 研究结果与分析

3.1 SWAT水文模型的参数率定与检验

SWAT 模型构建采用ArcGIS 10.2 环境下的Arc-SWAT 2012 版本。输入汉江流域的DEM 数据，使用模型推荐面积作为集水区划分的阈值，通过ArcSWAT自动提取水流方向和河流网络，获取模型所需要的地形参数、水系、汇流区域等信息，最终生成26 个子流域（图4）。在子流域基础上根据LUC、土壤数据和坡度范围使模型生成适量的水文响应单元（Hydrological Response Unit，HRU），每个子流域中LUC、土壤类型和坡度的唯一组合被定义为HRU，最终模型共生成303个HRU。

图4 汉江流域子流域划分及编号Fig.4 Division and numbering of sub-basin of Hanjiang River basin

3.1.1 模型参数率定

将1980年设置为模型预热期，1981-1995年为模型率定期，1996-2000年为模型检验期，通过Arc-SWAT 模型配套软件SWAT-CUP，应用SUFI-2 算法和全局敏感性分析方法，选取SCS 径流曲线系数、主河道曼宁系数和土壤蒸发补偿系数等13个对径流影响较大的输入参数［42，43］，同时对白河、黄家港、襄阳和皇庄4 个水文站1980-2000年的日平均径流数据进行参数率定和检验。采用相关系数（R2）、纳什效率系数（Nash-Sutcliffe Efficiency coefficient，NSE）［44］和偏差百分比（PBIAS）作为评价模型适用性的目标函数［45，46］，各指标计算公式分别如下：

式中：Qo，i为第i个观测径流，m³∕s；Qm，i为第i个模拟径流，m³∕s；为观测径流平均值，m³∕s；为模拟径流平均值，m³∕s；n为流量系列长度。

R2反映模拟值和观测值之间的线性相关性，其取值范围为0～1，其值越大，表示模拟值越接近观测值，模拟效果越好，一般认为R2＞0.6 时的模拟情况是可接受的［47］；NSE取值范围为-∞～1，NSE越接近1，表示模型模拟质量越好，模型可信度越高，一般认为NSE＞0.5 时的模拟情况是可接受的［48］；PBIAS反映模型模拟值和观测值的偏差程度，PBIAS=0表示模拟值等于观测值，PBIAS＞0 表示模拟值小于观测值，PBIAS＜0 表示模拟值大于观测值，即PBIAS绝对值越接近0，模型模拟效果越好，一般认为PBIAS绝对值＜25%时的模拟情况是可接受的［48］。

3.1.2 汉江流域SWAT水文模型径流模拟结果分析与讨论

从评价指标（表1）来看，4 个水文站的R2均在0.75 以上，PBIAS绝对值均在15%以内，除黄家港站检验期NSE为0.67 以外，其余NSE均在0.70 以上，各水文站的评价指标符合精度要求，说明SWAT模型在汉江流域的径流模拟结果是比较可靠的。

表1 汉江流域径流模拟评价结果Tab.1 Results of runoff simulation evaluation in Hanjiang River basin

为了更加直观地展示模拟径流与观测径流在径流峰值与枯水值的模拟情况以及二者拟合程度，分别绘制各水文站率定期和检验期的模拟径流与观测径流过程线（图5）及散点图（图6）。从图5、6 可知：①各站点在率定期和检验期模拟值和观测值都比较接近，模拟效果均良好，其中皇庄站径流模拟值和观测值最为接近，较其他各站效果好，而黄家港站模拟效果略差于其他各站；②各站点当径流观测值处于峰值时，径流模拟值也为峰值，但与观测值相比，模拟值偏低，当径流观测值为枯水值时，径流模拟值也为枯水值，但与观测值相比，模拟值偏高，可见模型对径流数据有一定的平均化作用；③模拟径流值与观测径流值线性相关性较好，散点分布在拟合直线1∶1的两侧，但部分点离拟合直线1∶1距离较远，这部分点主要为径流峰值点，由此可见，除径流峰值外，其余各点模拟效果较好。造成以上现象的原因可能是：皇庄站位于流域下游末端，水量充沛，河流调蓄能力强，因此模拟效果较好，黄家港站位于丹江口下游附近，观测径流受丹江口水库强大的调蓄作用影响，丰水期蓄水，枯水期补水，而模型则对天然径流进行模拟，因此径流模拟效果略差；另外，由于模型本身的不确定性，使其在峰值和枯水值上的模拟相对较差。最后，将率定好的SWAT 模型参数应用到汉江流域其他22 个子流域，便可得到各个出口断面的径流模拟值。

图5 汉江流域4个水文站率定期（1981-1995）及检验期（1996-2000）径流模拟结果过程线Fig.5 Runoff simulation results of four hydrological stations in Hanjiang River basin during calibration periods（1980-1995）and validation periods （1996-2000）

图6 汉江流域4个水文站率定期（1981-1995）及检验期（1996-2000）径流模拟结果散点图Fig.6 Scatterplot of runoff simulation results of four hydrological stations in Hanjiang River basin during calibration periods（1980-1995）and validation periods （1996-2000）

3.2 汉江流域生态流量计算

运用MTMMHC 法分别使用观测径流和模拟径流计算白河、黄家港、襄阳和皇庄水文站的生态流量，以皇庄站为例进行分析以检验由模拟径流所计算生态流量结果的合理性，若结果偏差较小则认为模拟数据较合理，可通过MTMMHC 法求得其他子流域的生态流量及Ea。再通过包括Tennant 法、年内展布计算法［49］、FDC法在内的水文学法分别计算汉江流域26个子流域出口的MEF，并分别按对应的时间尺度计算MEF占AAF或AMF的比值即MEF同期占比Ea（Tennant 法和年内展布计算法按年或月尺度计算的Ea相等，FDC 法按月尺度计算Ea），来对比各方法的优缺点，以皇庄站为例进行对比分析。

各方法MEF计算公式如下所示：

式中：MEFT、MEFN和MEFF分别为由Tennant 法、年内展布计算法和FDC 法所计算MEF，m³∕s；η为年内展布计算法中同期均值比；AAFmin为多年最小年均径流量，m³∕s。

MEF同期占比Ea计算公式为：

式中：Ea_y和Ea_m分别为年尺度和月尺度下的生态基流同期占比；MEFy和MEFm分别为按年尺度和月尺度计算的最小生态流量，m³∕s。

3.2.1 MTMMHC法生态流量分级

各子流域出口处MEF（ij）～OEFmin（ij）之间分级数经计算取为3 级，则各子流域出口处生态流量总共为4 级，各级生态流量分别表示为MEF、E2、OEFmin和OEFmax。

3.2.2 生态流量计算结果分析与讨论

表2是皇庄站出口断面分别由观测值和模拟值计算的不同月份在不同水平年的各级生态流量取值，其过程线见图7。结合表2和图7可知：针对皇庄站各月份的不同水平年组，在丰水年由观测值计算的MEF、E2、OEFmin和OEFmax的最大值均出现在7月或8月，由模拟值计算的除MEF最大值出现在9月，其余均出现在8月；在平水年由观测值和模拟值计算的MEF、E2、OEFmin和OEFmax的最大值均出现在8月；在枯水年由观测值计算的MEF、E2、OEFmin和OEFmax的最大值均出现在8月，由模拟值计算的除MEF最大值出现在8月，其余均出现在7月；各级生态流量的最大值都出现在同一个或者相邻的月份，各级生态流量的总体变化趋势是基本一致的。总体上，由观测值和模拟值计算的MEF、E2、OEFmin和OEFmax分别对应接近，对其微小差异可忽略，产生这一微小差距的原因可能是：计算月尺度下生态流量时，采用模拟日径流数据绘制逐月FDC，MEF的计算与Q90和Q95的大小息息相关，基于MEF计算的其他各级生态流量的计算也受到Q90和Q95的影响，而模拟径流数据与观测径流数据所求得Q90和Q95不同，计算的生态流量也会因此有略微差距。

表2 皇庄站以观测数据和模拟数据计算的各级生态流量取值对比m3∕sTab.2 Comparison of values of ecological flow at different levels calculated by observed data and simulated data at Huangzhuang hydrological station

将由Tennant 法、年内展布计算法、FDC 法和MTMMHC 法计算的MEF对应Ea分别表示为Ea_T、Ea_N、Ea_F和Ea_M，皇庄站各方法对应Ea见图8。从结果上来看：①Ea_T和Ea_N、均为定值，其中Tennant 法不能很好地考虑流量的逐月或年际变化，而年内展布计算法虽能够较好地体现年内各月河流天然径流的变化过程，但从计算上来看，采用最小年均径流这一最枯的情况代表所有情况，对天然径流年际丰枯变化的考虑较少；②MEFF和Ea_F在各月均取不同值，虽考虑了年内各月流量差异，但未考虑流量的年际丰枯变化；③Ea_M则不仅在年内各月都取得不同值，在同一月份的不同水平年也取得不同值，能充分考虑流量年内分布不均和年际变化的特点，体现了Ea在丰、平和枯年份的差异性。

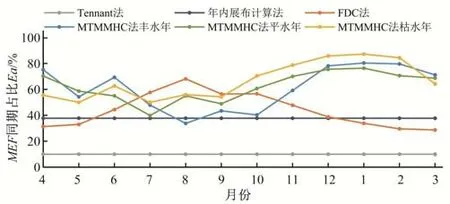
图8 皇庄站分别以Tennant法、年内展布计算法、FDC法和MTMMHC法计算的生态基流同期占比Fig.8 Comparison of the proportion of minimum ecological flow in the same periods calculated by four methods at Huangzhuang hydrological Station

结合图7、8 我们可以发现，在河道流量较大的月份Ea_F和MEFF均较大，MEFM也具有此特征，且MEFM在丰、平、枯年份间是逐渐减小的，但Ea_M并不具在流量大的月份大的规律，在丰、平、枯年份间也不是逐渐减小的，这与FDC 法很不同。这是因为在河道流量较大的月份，虽然MEF较大，但可能出现AMF远大于MEF使Ea较小，或月内逐日流量都很大，但AMF与MEF较接近使Ea较大的情况；在河道流量较小的月份，虽然MEF较小，但也可能出现AMF与MEF相差较大使Ea较小，或月内逐日流量都很小，但AMF与MEF较接近使Ea较大的情况。相对而言，流量大的月份Ea较小和流量小的月份Ea较大的情况比较容易出现。

图7 皇庄站以观测数据和模拟数据计算的各级生态流量及其占比Fig.7 Comparison of ecological flow and its proportion at different levels calculated by observed data and simulated data at Huangzhuang hydrological Station

3.3 汉江流域水资源开发利用率阈值结果分析与讨论

在计算汉江流域各子流域出口断面月尺度不同等级生态流量的基础上，求得满足不同等级生态流量要求的水资源开发利用率阈值（当月可开发利用水资源量占当月水资源总量的比值），u1、u2、u3和u4分别为MEF、E2、OEFmin和OEFmax所对应的水资源开发利用率阈值。

根据本文水资源开发利用率阈值的计算方法，Tennant法对应OEFmin即最适宜生态流量取60%AAF时的水资源开发利用率阈值对应现行40%的标准，故取由MTMMHC 法求得OEFmin对应的u3作为本文推荐的最适宜水资源开发利用率阈值。为反映汉江流域u3的时空分布特征，分别绘制了不同子流域各月份在丰、平、枯年份的u3空间分布图（图9～11），由图9～11 可知：①总体上，丰、平、枯年份丰水期（5-10月）u3相对于除丰水期外的其他月份（1、2、3、4、11和12月）而言较大，且多数子流域各月u3处于20%～40%及以上，其中7-9月的u3较5、6、10月而言更大，多数子流域在除丰水期外的月份u3＜20%；②在丰水年丰水期，仅有6 个子流域在各月出现u3＜20%共8 次，出现的频率仅为5.1%，其余u3都在20%～40%及以上，在7-9月大多数子流域各月u3在40%～60%及以上，在丰水期外，各子流域在各月u3＜20%出现的频率为70.5%；③在平水年丰水期，仅有4 个子流域在各月出现u3＜20%共7 次，出现的频率仅为4.5%，其余u3多数在20%～40%，在7-9月少于一半频次u3在40%～60%及以上，有2个子流域在各月出现u3＜20%共3 次，其余则在20%～40%及以上，在丰水期外，各子流域在各月u3＜20%出现的频率为77.6%；④在枯水年丰水期，多数子流域各月u3在20%～40%，仅有7 个子流域在各月出现u3在40%～60%及以上共14 次，出现的频率仅为9.0%，近一半子流域在各月出现u3＜20%共27 次，出现的频率仅为17.3%，在7-9月仅有6 个子流域在各月出现u3在40%～60%及以上共8次，仅有5个子流域在各月出现u3＜20%共5次，其余均在20%～40%，在丰水期外，各子流域在各月u3＜20%出现的频率为69.2%；⑤在除丰水期以外的月份中，各水平年u3大多在20%以下，低于现行40%的标准，总体上各子流域u3都较难满足现行40%的标准；⑥各子流域各月在不同丰、平、枯年份的u3均不同，体现了u3的时间和空间分布差异性。

图9 各子流域各月份在丰水年组的最适宜水资源开发利用率阈值Fig.9 The optimal threshold of water exploitation index of each sub-basin in each month in wet year

为保证河道内生态系统平衡以及防止水资源的过度开发，建议汉江流域在丰水年7-9月水资源开发利用率阈值可取40%，在丰水年丰水期除7-9月的其他月份以及平水年和枯水年的丰水期可取30%，除丰水期外的月份可取20%。

4 结论与展望

（1）利用SWAT模型模拟汉江流域径流过程，从径流过程线来看，径流模拟在峰值和枯水值上都略有欠缺，但从评价指标来看，4个水文站径流模拟结果均为良好，模拟精度达到了评价标准，说明SWAT模型能较好地应用于汉江流域径流模拟。

图10 各子流域各月份在平水年组的最适宜水资源开发利用率阈值Fig.10 The optimal threshold of water exploitation index of each sub-basin in each month in normal year

（2）通过MTMMHC 法计算有观测数据的4个子流域出口各月份不同水平年的各级生态流量，以皇庄站为例分析的结果表明，观测和模拟数据计算结果总体趋势基本一致，二者在数值上相差不大，认为模拟数据较为合理，可利用MTMMHC 法计算其他各子流域的生态流量。通过对比不同生态流量计算方法所计算生态基流占多年平均同期流量的比值，证明了MTMMHC法能同时考虑流量的年内和年际变化以及体现流量在丰、平和枯年份的差异性的优越性。

（3）通过河道内生态流量与水资源开发利用率阈值间的互补关系，求得各子流域各月份在丰、平、枯年份的水资源开发利用率阈值均不同，体现了水资源开发利用率阈值的时间和空间分布差异，反映了水资源开发利用率阈值的动态变化特征。

在以SWAT分布式水文模型模拟所得径流数据确定生态流量的基础上，计算了汉江流域各子流域各月份在不同水平年的各级水资源开发利用率阈值，体现了该阈值的时空分布特征。但文中所用的MTMMHC 法依旧是从水文学的角度上来计算生态流量，并不是完全按照生物学及物质循环角度，后续的研究中可以进一步考虑汉江流域不同鱼类和植物的生存环境以及通过动植物体内的物质循环推求其所需流量，以便在更好地满足生态需求基础上进行水资源的开发和利用。此外，水资源开发利用率阈值不仅仅与河道内生态流量有关，而且与开发利用能力、水资源系统特性和能源转化关系等有关，比如可从水资源系统回弹性角度进一步确定。

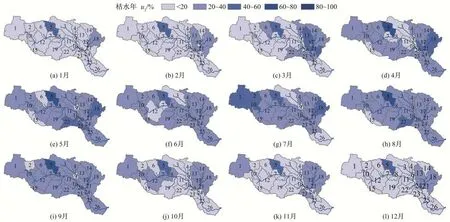
图11 各子流域各月份在枯水年组的最适宜水资源开发利用率阈值Fig.11 The optimal threshold of water exploitation index of each sub-basin in each month in dry year