HOG特征值的笔迹鉴定算法

2023-02-27王以松

智能计算机与应用 2023年2期

杨东，王以松

(贵州大学计算机科学与技术学院，贵阳 550025)

0 引言

统计学习理论(Statistical Learning Theory，SLT )是在20世纪60年代由Vapnik等人提出并于20世纪90年代中期建立的一种针对小样本情况研究统计学习规律的理论，由于解决了机器学习中小样本、过学习、欠学习和局部最小点等实际问题，从而成为20世纪90年代末发展最快的研究方向之一，其核心思想是学习机器要与有限样本相适应，从而实现最佳推广能力[1-2]。统计学习理论为小规模样本的机器学习问题提供了良好的理论框架，机器学习中的支持向量机(SVM)是最重要的算法之一，在诸多领域得到了运用[3]。郭辉[4]等人提出一种改进鲸鱼优化算法，同步优化SVM的特征选择模型，该算法的原理是利用Levy飞行策略对鲸鱼优化算法的螺旋更新位置进行变异扰动，改进了单纯形策略中的反射操作对种群中的精英个体，标准函数的测试结果证明，其改进能有效提高算法的收敛速度和计算精度。利用SVM核参数和特征选择目标作为共同优化对象，对UCI标准数据集和真实乳腺癌数据集进行特征选择仿真实验，真实乳腺癌数据集上的分类精度与传统支持向量机相比提高了11.053%。

方向梯度直方图(Histogram of Oriented Gradient, HOG)特征是在计算机视觉中用来对图片进行处理的一种特征描述子。HOG特征通过计算和统计图像局部区域的梯度方向直方图来构成特征[5]。韩松来[6]等人提出主成分分析(Principal Component Analysis，PCA)和 HOG特征的遥感异源图像匹配算法，利用HOG提取图像间的几何结构共性特征，能有效克服异源图像非线性灰度畸变的问题，实现多种遥感异源图像匹配性能的明显提升；宋建辉[7]等采用融入HOG特征对ResNet残差模型进行改进，利用自裁残差(Cropping Inside Residual，CIR)模型塑造的孪生目标可以增强跟踪网络的骨干网络对图形几何变化的鲁棒性；高达义[8]通过注意力模型(Convolutional Block Attention Module，CBAM)调节网络上下文信息的HOG特征比例，使网络中各特征图发挥出最好的效果。实验结果表明，该算法在OTB100的精确率和成功率分别达到81.9%和60.6%。

笔迹鉴定是司法领域的一个重要鉴定手段，张伟[9]等通过一起刑事申诉中的笔迹鉴定案例，阐述了笔迹鉴定意见在刑事审判中的关键性作用；张乐[10]等对中国裁判文书网平台的笔记鉴定意见资料进行归纳和分类，进而讨论笔迹鉴定在司法案件的应用，增强了笔迹鉴定意见的公信力，从而最大限度发挥笔记鉴定意见在诉讼案件中的证据作用。

目前，深度学习、强化学习等模型训练呈现训练规模大、时间长，对计算资源要求高的问题，在实际使用过程应用较为困难。本文探索提取笔迹HOG特征对笔迹的SVM模型进行训练，对笔迹的真伪进行鉴定。实验结果表明，该模型在较小的样本和较短的训练时间、资源条件下，能成功鉴定伪造笔迹。

1 算法思想

SVM(支持向量机)是定义在特征空间上通过求解间隔最大的线性分类器的二分类模型。SVM的求解问题可以形式化求解的凸二次规划问题中的间隔最大化，也等价于正则化的合页损失函数的最小化问题。SVM的学习算法就是求解凸二次规划的最优化算法[8]。本文提取笔迹的HOG特征向量，利用SVM算法训练出笔迹特征的HOG特征向量超平面。

1.1 SVM算法原理

SVM的基本算法思想是能够对训练数据集正确划分并且求解几何间隔最大的分离超平面。如图1所示，ω·x+b=0即为分离超平面，对于线性可分的数据集来说，虽然分离超平面可能有无穷多个，但是几何间隔最大的分离超平面却是唯一的。

几何间隔：对于给定的数据集T和超平面ω*x+b=0，定义超平面关于样本点 (xi，yi)的几何间隔，公式(1)：

(1)

SVM模型的求解最大分割超平面通过求解二次规划问题得到最小化泛函，式(2)：

(2)

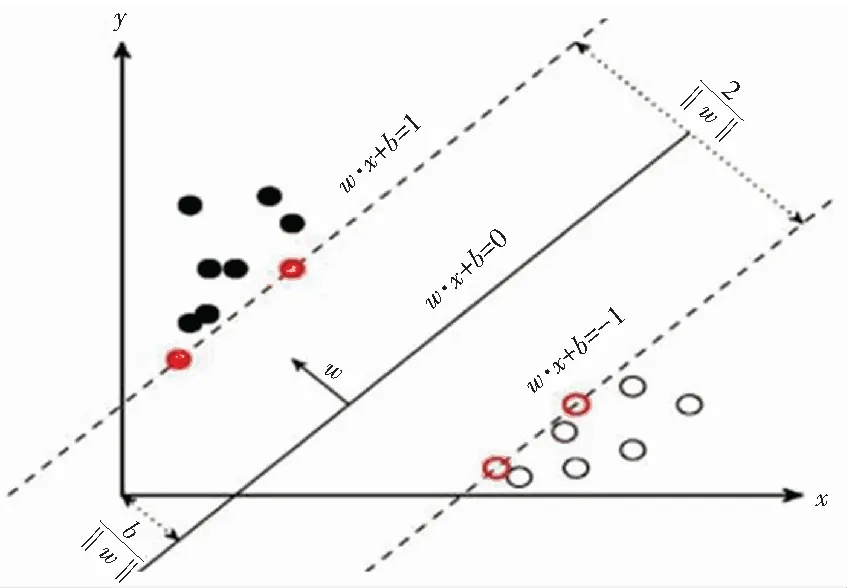
图1 SVM超平面图

约束条件为不等式类型：yi[(xi·ω)-b]≥1,i=1,2,3,…,l

这个优化问题的解是由拉格朗日泛函的鞍点给出的，式(3)：

(3)

其中，αi为拉格朗日乘子。

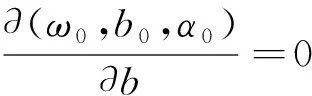
最优超平面具有两个特性：

(1)系数αi必须满足约束，式(4)：

(4)

(2)最优超平面，向量ω0是训练集中的向量的线性组合，式(5)：

(5)

只有所谓的支持向量可以在ω0的展开式中j具有非零的系数αi。不等式yi[(xi·ω)-b]≥1,i=1,2,3,…,l在等号成立时得到支持向量，其最优超平面，式(6)：

(6)

1.2 HOG特征向量的计算

纹理特征是图片的一种独特的特征。纹理作为反映图像同质现象的一种视觉特征，当物体表面具有缓慢变化或者周期性变化时，纹理就会体现出相应的变化。纹理的3大标志：非随机排列、某种局部序列性不断重复以及纹理区域内大致为均匀的统一体。纹理特征包含统计型纹理特征和模型纹理特征。统计型纹理特征从像元及其邻域内的灰度属性出发，研究纹理区域中的统计特征；模型纹理特征是假设图片纹理是某种参数控制的分布模型的形式，再以纹理图像的实现来估计计算模型参数[5]。HOG特征是描述局部纹理的有效特征向量，计算笔迹图片的HOG特征的方法为：将一张笔迹图片按照8×8像素的大小分割为若干个细胞单元，每个细胞单元中梯度角度的取值范围介于0～180°之间，将角度范围分成9份，每20°为一个组；在细胞单元中，对内部所有的像素的梯度进行统计；将每一组中所有像素对应的梯度值进行累加，可以得到9个数值。直方图就是由这9个数值组成的数组，每个细胞单元就会得到一个9维的特征向量，特征向量每一维对应的值是累加的梯度幅值。在获得每个细胞单元的梯度方向直方图后，再对细胞单元组合形成区块。在笔迹图片中，选取2×2个细胞单元作为一个区块，每次滑动8个像素得到一个新的区块，按照此步骤循环结束后得到整个笔迹图片的HOG特征向量。结合SVM的算法，可求解出笔迹图片中的HOG特征向量超平面。

2 实验步骤

本文的实验包括3个步骤：分别是图像预处理、计算梯度直方图并进行池化处理并训练模型，通过测试样本对模型进行检测。

(1)图像预处理包括伽马校正和灰度化。使用伽马校正减少光度对实验的影响。灰度化是将彩色图片变成灰度图，降低图片处理的计算量。考虑到本实验的笔迹均为黑白色，因此采用灰度图来处理。笔迹图片预处理后获取外部纹理特征如图2所示。

图2 笔迹图片预处理

(2)提取笔迹图片的HOG特征值，再对HOG特征值矩阵进行平均值池化处理，最终得到笔迹图片的HOG特征向量，如图3所示。

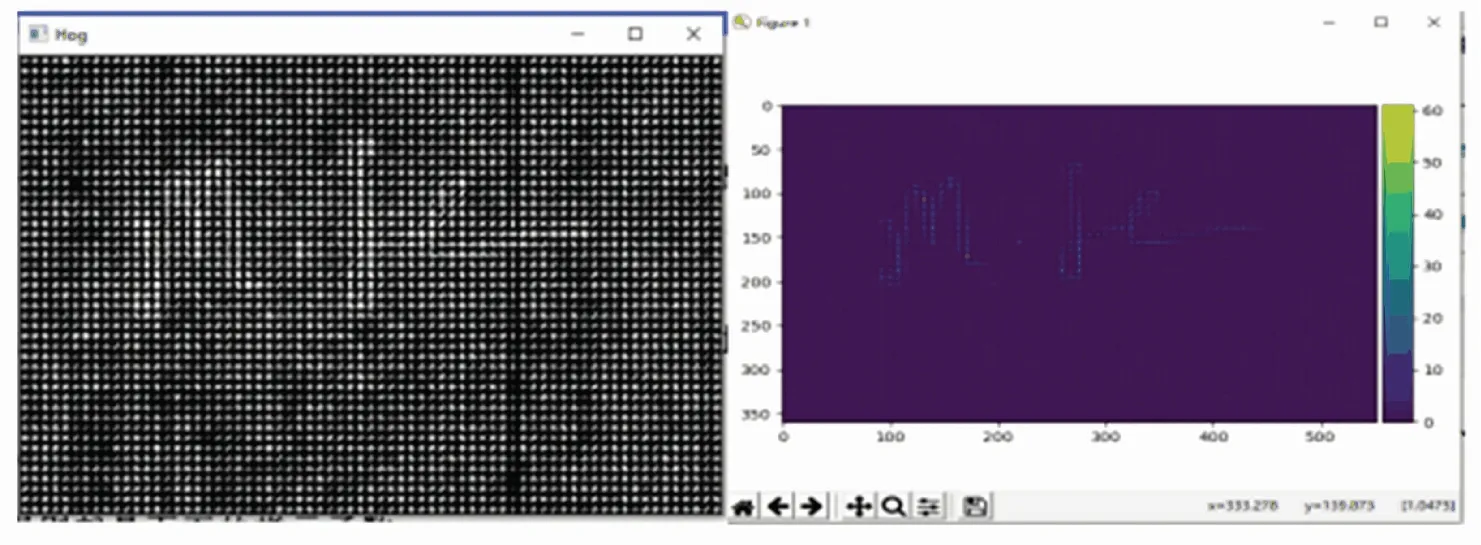
图3 笔迹图片的HOG特征向量

(3)通过测试样本对SVM模型的训练结果进行验证，如用仿冒的笔迹进行验证，则系统判定出属于仿冒的笔迹，且给出其属于仿冒笔迹的相应的概率值。两组数据分为训练数据组和测试数据组，而测试数据组则是用来检验模型是否可以对笔迹进行鉴别。通过人工标注方式对数据进行标注：本人笔迹标记label为1，仿冒笔迹标记为0。