基于螺旋光栅相位和分数Fourier的光学图像加密算法

车 凯， 王海翔， 白林亭， 文鹏程， 杨芷柔， 赵洪东

(1 中航工业西安航空计算技术研究所， 西安 710065； 2 西北工业大学 计算机学院， 西安 710072； 3 哈尔滨工业大学 计算学部， 哈尔滨 150001)

0 引 言

随着大数据时代的来临，图片数据存储量越来越大，原始的图像置乱加密的方法，已不能满足高效加密的需求。当前不仅需要的是安全性较高的加密方法，且实际场景应用要求加密系统在保证足够安全的前提下，对性能提出了要确保时效性较高、抵抗攻击的鲁棒性能要好、图像密钥占据空间要小、密文图像与明文图像的相似度小等众多要求[1-2]。

目前，在图像加密技术中，较为流行的方法主要分为两大类：混沌加密和光学加密[3]。混沌加密技术主要是利用复杂的相空间等特征，对图像像素及其值进行改变。虽然此类方法的加密效果较好，但混沌系统的周期性会造成加密安全性的缺失。为解决混沌加密安全性的问题，光学加密技术相继被提出，该技术具有效率高、存储量大、并行度高以及密钥维度多等特性。自1995年后，随着Refregier等人[4]提出经典的双随机相位编码光学加密系统后，一系列的光学加密方法相继被提出。2017年，Kumar[5]等人提出了一种新的非线性光学图像加密技术，使用螺旋相位变换(SPT)，采用随机相位掩码(RPM)调制，使得图像以距离z进行菲涅耳传播，以达到加密的效果。但是，复杂的菲涅耳变换会增加计算的难度。同年，Kumar等[6]又提出了利用小波变换替换分数傅里叶变换，并分析了不同融合方法的优缺点。2018年，Khurana M[7]提出了一种基于混合结构相位掩模(HSPM)的旋转变换(GT)域双图像加密方法，使光学图像加密方法鲁棒性得到提升。

为了同时提高鲁棒性和加密效率，本文在使用螺旋相位作为部分密钥的基础上，引入错位光栅生成的涡旋光束作为部分密钥，提出了一种基于螺旋光栅相位和分数Fourier的光学图像加密算法。利用计算全息法设计位错光栅并生成涡旋光束，然后与自主设计的螺旋相位结合形成加密密钥，使用分数傅里叶变换对图像进行加密。经统计直方图、信息熵、差异性和抗噪声攻击能力等实验分析，表明该方法具有很好的鲁棒性和安全性。

1 基于螺旋光栅相位和分数Fourier的光学图像加密算法

1.1 螺旋相位变换(SPT)

在螺旋相位变换中，二维符号函数sgn(μ,ν)也被称为螺旋相位函数(SPF)，用于二维Hilbert变换[8-9]。二维符号函数可以定义为空间频率中的纯SPF：

(1)

其中，相位φ(μ,ν)是频率空间中的极坐标角。SPF函数未在原点处定义，其在原点处的值可以是0或1，这些值指向奇点。

在此情况下，通过引入参数q来修改SPM函数。q是奇点的数量或SPF的阶，对应于SPF值未定义的点(即0或1)。修改后的SPF可改写为

SPF=exp{iqφ(μ,ν)}

(2)

因此，对于特定阶的SPF，二维信号的SPT可以表示为

SPF{f(x,y)}=IFT{SPF.FT{f(x,y)}}

(3)

其中，FT和IFT分别表示二维傅里叶正变换和反变换。

SPT的逆为

ISPF{f(x,y)}=IFT{conj(SPF).FT{f(x,y)}}

(4)

其中，conj()表示共轭复数。

1.2 计算全息法生成涡旋光束

涡旋光束是一种具有螺旋状相位波前的光束，且在传播方向上，光束中心强度或轴向强度为0，又被称为暗中空光束[10]。涡旋光束具有暗斑尺寸极小、光强呈环状分布和传播不变性等独特的物理特性，因此涡旋光束被广泛地应用在光学计算、物理数学和信息处理等方面。

通常，涡旋光束的获取有多种方法，如：计算全息法、几何光学法和中空波导法等[11]。以上方法中，基于计算全息法适用范围广，能够便捷地生成不同阶的涡旋光束。

假设：E1exp(iφ1)和E2exp(iφ2)分别表示两个光束的波函数，当两束光发生干涉时，产生的干涉光强则为

(5)

其中，2E1E2cos(φ1-φ2)表示干涉光强的空间分布特性，通常选择其作为光栅透过率函数来产生光栅。将E1exp(iφ1)作为参考光束，通过照射光栅，光束E2exp(iφ2)能够在透射光束中再现，即为全息术的原理。

计算全息法就是基于全息术原理，利用已有光束来获取所需的具有某种特性的光束。由于光栅的种类可以不同，透射光束也就不同，造成了透射光束的多样性和不确定性，这正是生成密钥所需要考虑的形式之一。因此，本文选择计算全息法产生的涡旋光束相位作为密钥的一部分。

1.3 分数傅里叶变换

分数傅里叶变换是1980年Namias[12]为求解偏微分方程而引入量子力学。1993年，Mendlovic等[13]人通过研究光在二次梯度折射率介质中的传播，给出了分数阶傅里叶变换级数形式的表达式。同年，Lonmann用Wigner相空间旋转的概念，给出了分数傅里叶变换的积分形式表达式[14]。

设f(x)为输入信号，则其P阶分数傅里叶变换定义为

(6)

1.4 加密算法的实现

加密流程如图1所示，其实现的具体步骤如下：

Step 1将原彩色图像转化为灰度图像，再将灰度图像转换为double值;

Step 2利用SPT自行设计一个螺旋相位，记为p1；

Step 3利用计算全息法模拟错位光栅产生的涡旋光束相位，记为p2；

Step 4将p1和p2组成密钥p；

Step 5利用密钥p，采用分数傅里叶变换对double值图像进行处理，即得到加密图像。

图1 加密计算流程图

与之对应的解密过程为：利用相同参数的加密密钥图像，输入加密参数相反数，对加密图像进行分数傅里叶变换，即可以得到加密之前的灰度图像。还可恢复原来色彩，得到原始彩色图像。具体解密流程如图2所示。

图2 解密计算流程图

2 实验仿真与算法性能分析

仿真实验选取大小为512*512的“Lena”彩色图像。首先，采用本文提出的加密算法进行实验；其次，以统计直方图、信息熵、差异性和抗干扰能力等评价指标与其它加密算法进行比较。实验表明，本文提出的加密算法具有很好的安全性和有效性。

2.1 加密实验

在不进行任何攻击测试的前提下，测试了加密的全过程，实验结果如图3所示。

图3 无攻击情况下的加密过程

其中，加密处理结果的放大效果如图4所示。

早期的唐草风格基本指的就是亚利桑那和加州风格。其特点是纹样的边线处理不规则，并且随型的比较多。之所以叫亚利桑那风格,是因为图案中出现的花卉纹样是采用亚利桑那特有花卉图案。花托部分的装饰线条是Y形纹排列，中间用刀线从上往下隔开。装饰性的茎干数量小，弧度小，卷草粗大，头部收缩卷曲，用圆点图案在中心收节。枝叶部分是采用欧式的茛苕叶。刀线走得窄而深。

图4 放大后的加密结果

2.2 算法安全性及性能分析

2.2.1 统计直方图分析

首先，对明文图像和密文图像的统计直方图进行了对比，实验结果如图5所示；其次，为了对比明文图像与解密图像的差异性，对两者进行了统计分析，实验结果见图6；最后，对经典的混沌加密算法、块置乱加密算法、像素置乱加密算法和CaTmap加密算法的实验结果进行了统计图分析，实验结果如图7～图10所示。

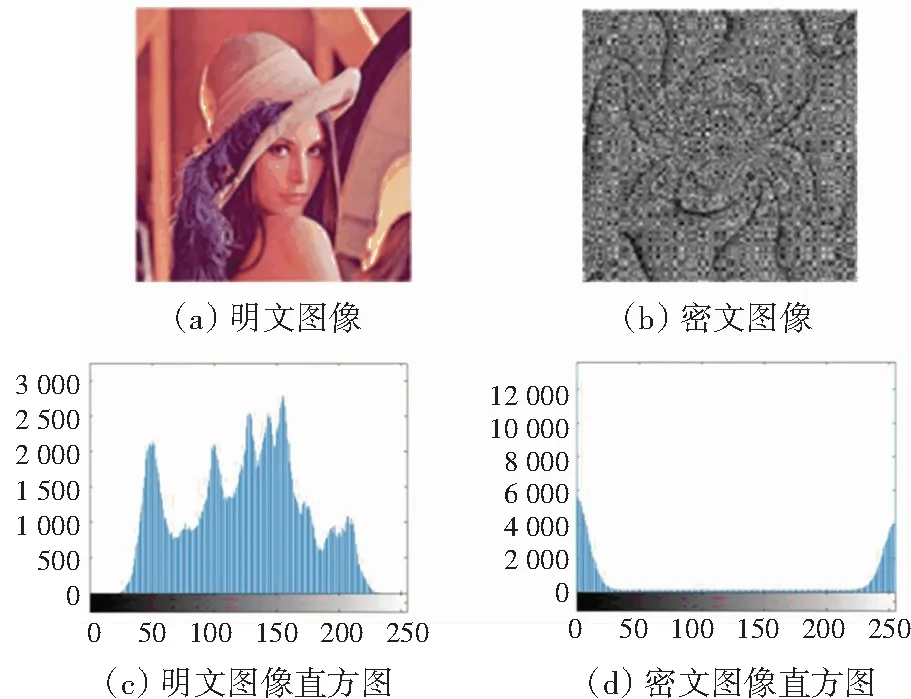
图5 本文方法的明文和密文图像直方图

图6 本文方法的明文和解密图像直方图

图7 混沌加密算法的明文和密文图像直方图

图8 块置乱加密算法的明文和密文图像直方图

图9 像素置乱加密算法的明文和密文图像直方图

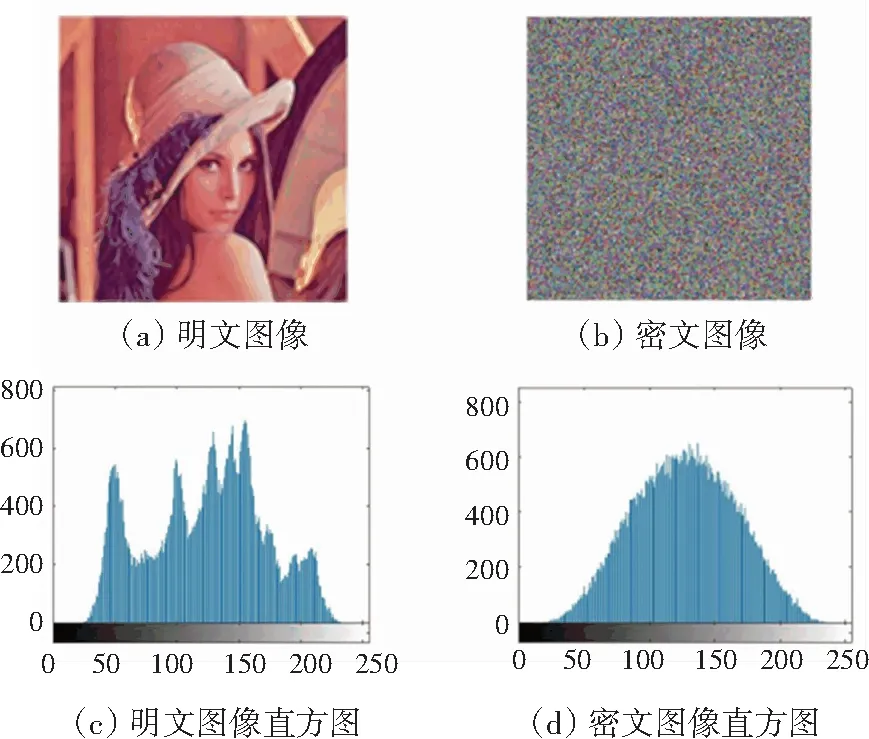
图10 CaT Map加密算法的明文和密文图像直方图

由多组实验对比可以看出，本论文提出的加密算法在统计规律上，停留在像素值为0～35和220～155这个区域，这是由于图像的加密算法中的密钥造成的。从密文图片可见，整体可以看出融合密钥的纹理信息，这也从侧面说明了统计图的结果。

2.2.2 信息熵分析

信息熵表示信息的混乱程度，图像的信息熵越接近理想值，则表示其信息越混乱，也说明其加密效果越好[15]。通常，加密图像信息熵的理想值为8。本文所提算法加密后图像的信息熵为7.995 85。

设图像m的信息熵为H(m)，其定义为

(7)

其中，p(mi) 表示信息值mi出现的概率。

2.2.3 差异攻击分析

当明文图像中的微小变化在密文像素中产生巨大差异时，图像加密方法对于差分攻击具有较强的抵抗力。这种类型的分析通过像素变化率(NPCR)和均匀变化强度(UACI)来度量。本文方法与Jan Sher Khan[16]的方法在NPCR和UACI上进行了对比，实验结果见表1。结果表明，本文方法具有良好的差异攻击性。

表1 NPCR 和 UACI 测试数值的对比结果

2.2.4 噪声攻击分析

为了验证加密算法在抵抗密文攻击时的鲁棒性，本文验证了抗噪声干扰的能力。在密文图像中加入高斯噪声。

G′=G(1+Kσ)

(8)

其中，G和G′分别表示密文图像和攻击后的图像；K表示噪声强度系数；σ表示加入的随机噪声。

图11为加入不同噪声后灰度图像的解密结果。Lena的解密图像能够被识别出来，当K=0.6时，解密图像仍能够被识别出来，表明该加密算法对噪声攻击具有较强的鲁棒性。

(a) K=0.1 (b) K=0.3 (c) K=0.6

3 结束语

本文提出了一种基于螺旋光栅相位和分数Fourier的光学图像加密算法。该方法的密钥融合了螺旋相位和错位光栅生成的涡旋光束，在利用分数傅里叶变换对图像进行加密处理。仿真实验从统计直方图分析、信息熵分析、差异性分析和抗噪声攻击能力分析等方面进行验证，实验结果表明该方法具有很好的加密效果、鲁棒性和安全性。