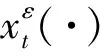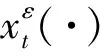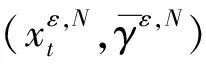具有随机切换的泛函Liénard方程的平均法
2023-02-27徐燕李彩月
徐燕,李彩月
(河北大学 数学与信息科学学院,河北 保定 071002)
随机微分方程作为一种动态模型,广泛应用于复杂的生物、物理、化学和工业等领域.在自然界和工程实践中,由于随机扰动的影响许多现象或过程具有多尺度特征.例如:在经典的基因表达模型中,由于转录过程快于翻译过程,所以可用双时间尺度系统刻画,另外,地理方面的大气和海洋现象等许多物理现象也都具有空间或时空的多尺度特征,因此,用多尺度系统理论来描述或分析这些现象或过程是十分有必要的.对于多尺度的定性分析,平均法提供了极大帮助.多尺度的随机微分方程的平均法就是在一定的条件下,将快变量过程视为随机噪声并将其消除从而得到一个极限过程,使得极限过程的解逼近原始方程中慢变量的解.
平均法广泛应用于力学、物理、控制等领域,是简化动力系统从而得到微分方程近似解的有力工具.平均原理首先由Krylov等[1]提出,而后由Gikhman[2-3]推广到非线性常微分方程.1968年,Khäminskii[4]首次将平均法推广到随机微分方程.此后,随机微分方程的平均法便引起学者们广泛关注.文献[5-8]讨论了在Lipschitz条件下的双时间尺度随机微分方程的平均法.Xu等[9]拓展文献[5-8]中的结果,将平均法应用到非-Lipschitz条件下的随机微分方程.通过消除快变量建立了耦合系统平均方程存在定理,从而将系统简化为单个随机微分方程.结果表明,该慢变量强收敛于相应的平均方程的解.
另一方面,某些过程在已知现在时刻所处的状态条件下,其在将来时刻处的状态,只与过程在时刻所处的状态有关,而与过程在时刻以前所处的状态无关.当在不确定性条件下的实际系统出现这样的过程时,通常使用Markov模型.Yin等[10]收集了分散在其他关于Markov链文献和奇异摄动的一些观点.但在处理不确定条件下的实际系统时,往往非常复杂.因此,希望将一个复杂的、大维度的系统划分为许多更简单、低纬度的子系统,否则,即使有强大的计算设备,也很难处理.同时,Markov链通常受制于频繁的波动,为突出空间状态中不同的波动速率,引入一个小参数ε>0,可以表明Markov链在单个状态Wk中波动很快,但从状态Wi跳跃到状态Wj却很慢(i≠j).因此,在Wk中的状态可以聚合为一个状态k.这样通过分离-聚合的思想从而使潜在的问题是可解决的.对于此类的Markov模型,Yin[11]推广了一般的保险风险模型,研究了由连续时间Markov链调制的双时间尺度跳跃扩散模型,其中,Markov链在文章中表示保险风险模型在不同的社会环境中所处的状态.Yin等[12]利用平均法研究了具有随机切换的随机Liénard方程,对于系统中同时出现的连续变量(随机Liénard方程的解)及离散变量(在很大但有限的状态空间中的Markov链),结合分离聚合的思想、鞅问题公式,得到一个弱收敛结果.
随机微分方程的平均法已经取得了很大的进展,但对于随机泛函微分方程的平均法的研究却很少.Dupire[13]利用分段泛函导数建立了泛函It公式,量化了路径在端点处的泛函变化.泛函It公式的建立改变了随机泛函微分方程的发展格局,解决了许多由于长期缺乏工具而无法解决的问题,并为随机泛函微分方程的发展奠定了基础.Wu等[14]拓展泛函It公式到混合泛函微分方程的It公式,利用混合泛函It公式和鞅表示定理得到具有双时间尺度的路径相关泛函扩散系统的渐进性质.受此启发,本文将泛函It公式应用到具有随机切换的泛函Liénard方程,利用平均法得到随机泛函Liénard方程的平均方程, 得到的极限过程可以用于逼近和计算分析原始方程, 以降低计算复杂度.
1 预备知识和符号假设
定义过程xt={x(σ∧t):0≤σ≤T}为[0,T]上的函数,即有效信息始终在[0,T]内,其中xt表示对历史的依赖;R2表示具有欧几范数|·|的2-维欧几里得空间;D([0,T];R2)表示在[0,T]内右连左极且取值在R2内的函数空间,其范数定义为最大范数‖·‖∞;C([0,t];R2)为从[0,T]到R2的连续函数族;对任意N>0,BN={x:|X| 首先,给出水平导和垂直导的相关概念. 定义1[15]设xt={x(σ∧t):0≤σ≤T},若非预期泛函F:[0,T]×D(0,T];Rn)→R的极限 存在,则非预期泛函F在(t,x)∈[0,T]×D([0,T];Rn)处水平可微,称DF(t,x)为F在(t,x)处的水平导数. 定义2[15]设xt={x(σ∧t):0≤σ≤T},若泛函映射e→F(t,xt+e1[t,T])在0处可微,则非预期泛函F:[0,T]×D([0,T];Rn)→R在(t,x)∈[0,T]×D([0,T];Rn)处垂直可微,其在0处的梯度称为F在(t,x)处的垂直导数: xtF(t,x)=(∂1F(t,x),…,∂nF(t,x)), 其中, 如果F对所有(t,x)∈[0,T]×D([0,T];Rn)垂直可微,则称非预期泛函xtF为在(t,x)处的垂直导数. 在完备的概率空间(Ω,F,P)中,研究以下系统: (1) 基于上述讨论,给出以下相关假设. 因此,系统(1)可以写为 (2) 因此,相关算子为 (3) 利用随机平均法,得到系统(2)平均后的方程 (4) 其中, 定义截断函数为一个平稳函数,使得 当x在半径为N的球内时其截断为1,在半径为N+1的球外时其值为0,且是光滑连通的.因此可将方程(2)写为 (5) 假设H1)说明了f(xt,l,t)在x处有界保持,且f(xt,l,t)在[0,T]上关于γε连续有界,印证了f(xt,l,t)∈Cb(R2;W,[0,T]),由此可得fN(xt,l,t)是有界的.同理可得对任何x∈D([0,T];BN),gN(xt,l,t)和hN(xt,l,t)是有界的. (6) 为讨论Xt的胎紧性,需要下面的定理. 如果存在一个随机变量Φε(σ),对任意0≤s≤σ,t≤T使得 为得到本文主要结果,给出以下引理. 引理2在假设H2)的条件下,对于i=1,2,…,l,j=1,2,…,mi以及有界可测确定函数βij(·),有 证明见文献[10]引理7.18. (7) 将系统(5)代入式(3),有 由引理2,可知 (8) 关于其余项,应用引理2以及dl的有界性可得 可得 (9) 结合式(8)和式(9)可得 (10) 同理,有 (11) 因此应用相同的技巧,可得 (12) 同时,有 (13)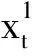
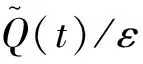

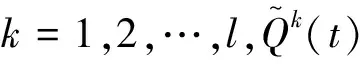

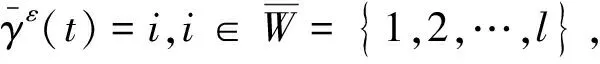
2 鞅问题方法