锆石辐射损伤测年方法研究进展与应用
2023-02-27范明璞柳小明孙圣思
范明璞,柳小明,孙圣思
大陆动力学国家重点实验室,西北大学地质学系,西安,710069
内容提要:锆石辐射损伤测年是一种新兴的低温热年代学方法(封闭温度为~230 ± 25℃),其原理是依据拉曼半高宽(ν3)计算出锆石所累积的α通量,结合U、Th含量,得出锆石辐射损伤的累积时间,即锆石辐射损伤年龄。相较于其他低温年代学方法,锆石辐射损伤测年具有测试简便、高效、低成本、双(多)定年等优势,在地学研究中展现出广泛的应用前景,现已成功应用于示踪物源区和揭示岩体热事件等领域。然而,该方法尚存几个关键问题有待解决,例如,微区测试的空间不匹配性、封闭温度存有争议、较大的年龄偏差等,这无疑阻碍其在地球科学领域中更进一步的推广和应用。本文系统地介绍了锆石辐射损伤测年方法的起源、原理和测试方法,总结了相关应用的重要进展,阐述了锆石辐射损伤测年方法的尚存问题,并对该方法的发展趋势作以展望,以期为年代学的发展提供新的技术手段。
锆石是一种普遍存在于地壳岩石中的副矿物,具有良好的物理、化学稳定性,且晶格中放射性元素U、Th含量较高(普通Pb含量极低),现已成为年代学研究中最为理想的矿物之一。目前,已有多种测年技术成功应用于地质过程中,例如,U-Pb、Pb/Pb、裂变径迹和(U—Th)/He方法(Reiners et al., 2005)。随着科学研究的不断深入,新方法、高效率、高精度、高空间分辨率和多信息的同时获取已成为年代学领域发展的必然趋势(李献华等,2022)。
1 锆石辐射损伤测年方法发展史
20世纪初,Hamberg(1914)提出不同锆石物理性质的差异是由于放射性元素(不同含量)衰变产生的高能量α粒子对晶格的破坏所引起,即随着U、Th的不断衰变,锆石晶格的稳定性逐渐遭受破坏,导致其物理性质持续发生变化,例如,密度、折射率、双折射率不断减小,晶格逐渐膨胀等。随后,该理论已被研究证实和广泛接受(Chudoba and Stackelberg, 1936; Anderson and Payne, 1937; Bauer, 1939)。20世纪50年代,研究者们首次提出,这些物理性质及参数的变化可能被用作地质年代计(Holland and Kulp, 1950; Kulp et al., 1952; Hurley and Fairbairn, 1953)。同期,Holland和Gottfried(1955)利用X射线衍射技术对斯里兰卡锆石的密度和晶胞参数进行测定,结合U-Pb年龄及U、Th含量得出α通量,试图建立α通量与晶胞参数和密度的函数关系。但是,斯里兰卡锆石与其他地区锆石的晶胞参数存有差异,研究者们将其解释为该锆石经历了部分热退火,这一认知对构建辐射损伤的标定曲线增加了一定难度。后期研究证实,遭受辐射损伤的锆石的确会发生热退火作用(Bursill and Mclaren, 1966; Pidgeon et al., 1973; Meldrum et al., 1998; Geisler et al., 2001)。20世纪50年代末,随着同位素稀释法对锆石U-Pb年龄精确测试的出现(Tilton et al., 1955; Silver and Deutsch, 1963),以及年代学对辐射损伤微区精准测定的需求,锆石辐射损伤年代学可能作为一种测年技术已被基本遗弃。
然而,对于锆石辐射损伤的研究并未停止,并且已积累了多种表征方法,例如,粉晶质衍射(Murakami et al., 1986)、X射线吸收(Nakai et al., 1987; Farges and Calas, 1991)、核磁共振(Kalinichenko et al., 1990)等,但这些技术对于辐射损伤的定量评估却存有较多不足(耗时、不精确等)。随后,Nasdala等(1995)利用LRM对锆石的辐射损伤进行测试,指出随着辐射损伤的累积,锆石晶格不断遭受破坏,使得拉曼峰位值逐渐向低波数漂移、半高宽(FWHM,full width at half maximum)不断增大且强度逐渐变低,并且认为~1008 cm-1拉曼特征峰所对应的半高宽能够定量描述锆石的辐射损伤程度(最为敏感),为后期建立辐射损伤(FWHM)与α通量的校正曲线以及利用拉曼光谱法进行测年提供了可能。值得一提的是,这一技术相较于其他测试方法而言,最大的优势在于:测试迅速、低成本、无需特殊制样、无损且精度高,可用于微区辐射损伤的定量评估。
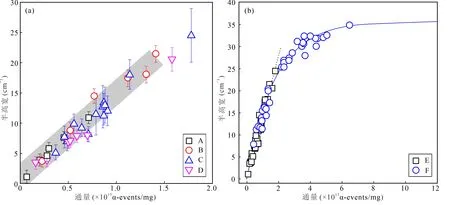
图1 α通量与半高宽关系图
2 蜕晶化和热退火作用
锆石自形成之后,由于其所含放射性元素U、Th的持续衰变,随着时间的推移,锆石晶格逐渐由晶体质向蜕晶质转化,最终趋于无定型状态,即蜕晶化作用(Metamictization)。自然界中,大部分锆石处于蜕晶质或无定型状态,且蜕晶化程度主要取决于所包含的U、Th含量,结晶年龄(形成时间)以及后期经历的热事件。并且,在地质演化过程中,如果蜕晶质锆石在形成之后经历过低温或高温热事件(温度增加至足以使锆石的辐射损伤结构发生愈合),那么该锆石就会发生热退火作用(Annealing),引起晶格中移位的原子获得能量后重新回到初始位置,从而使得辐射损伤的晶格逐渐愈合以至于恢复至晶体质状态。20世纪以来,由于为人所知的宝石级斯里兰卡锆石具有全范围的辐射损伤、含有的杂质较少且展现出一致的热演化史等特性,已是研究锆石蜕晶化和热退火作用的绝佳样品(Holland and Gottfried, 1955; Murakami et al., 1991; Nasdala et al., 1998, 2001, 2003; Farnan, 1999; Rios and Salje, 1999; Salje et al., 1999; Rios et al., 2000a, b; Zhang Ming et al., 2000a, b, c; Farnan and Salje, 2001; Palenik et al., 2003; Ginster et al., 2019; Ende et al., 2021)。
2.1 蜕晶化作用
自Hamberg(1914)首次提出锆石的蜕晶化过程是由于U、Th衰变引起锆石晶格由周期向非周期性阶段性转化之后,已积累了多种用以描述锆石蜕晶化作用的测试方法和物理参数(不同尺度),例如,X射线衍射(晶胞参数)、红外和拉曼光谱(峰位值、峰宽和强度)、透射电镜和核磁共振(成像)、折射率、双折射率、密度、热荧光性、硬度、泊松比等(Pabst, 1952; Holland and Gottfried, 1955; Vance and Boland, 1975; Chakoumakos et al., 1987; Weber, 1990; Murakami et al., 1991; Weber et al., 1994; Nasdala et al., 1995; Farnan, 1999; Salje et al., 1999; Zhang Ming et al., 2000b, c; Geisler et al., 2001; Ewing et al., 2003; Palenik et al., 2003)。Murakami等(1991)对一系列斯里兰卡锆石(不同辐射损伤程度)展开研究,结合高分辨透射电镜成像特征和X射线衍射分析,根据该锆石所累积的α通量,将辐射损伤的累积过程划分为3个阶段:第一阶段是点缺陷的累积,引起锆石晶胞的轻微膨胀和乱序,对应的α通量为<3×1015α/mg;第二阶段是晶格发生扭曲,逐渐向无定形转变,而晶格结构仍以晶体质为主,对应的α通量为3×1015~8×1015α/mg;第三阶段是锆石晶格完全处于无定型状态,对应的α通量为>8×1015α/mg。并且,依据拉曼光谱(ν3)的变化,可将锆石结构划分为晶体质(或轻微乱序)、蜕晶质和高度蜕晶质(无定型),对应的峰位值和半高宽分别为:~1007 cm-1、≤5 cm-1(或<10 cm-1),1000~980 cm-1、10~20 cm-1和<980 cm-1、>30 cm-1(Nasdala et al., 1995, 1998)。随后,基于“渗滤相变”理论对锆石的蜕晶化过程分析得出,锆石晶格由晶体质向无定型状态的转变存在2个阈值(渗滤点),即锆石晶格中孤立的“岛(点缺陷)”逐渐增加至长程连通状态时到达第一渗滤点(~3×1015α/mg);且随着非晶质物质占比的增加,锆石晶格基本处于无定型状态时到达第二渗滤点(~8×1015α/mg)(Salje et al., 1999)。而根据天然锆石(斯里兰卡和萨克森锆石)拉曼峰位值和半高宽的变化,可将锆石的蜕晶化过程划分为2个阶段(图2a):第一阶段是点缺陷的累积,代表短程乱序的增加;第二阶段是长程有序的破坏,锆石晶格向无定型过渡,非晶质形成(Geisler et al., 2001)。后期,Pidgeon(2014)通过斯里兰卡锆石辐射损伤累积曲线对早期所提出的两阶段α通量进行修正,渗滤点分别对应于~2.2×1015α/mg和~5×1015α/mg。
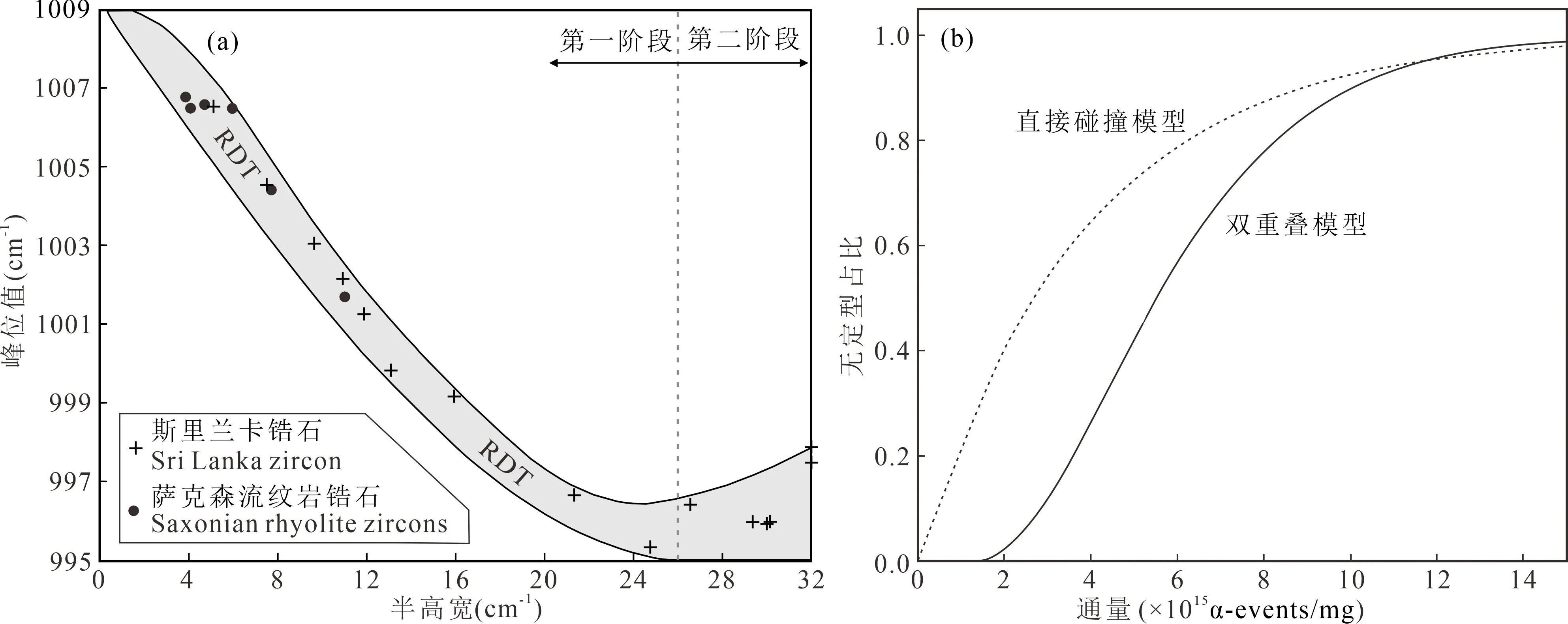
图2 蜕晶质锆石峰位值与半高宽关系图(a)(据Geisler et al., 2001修改)和锆石晶格无定型占比与α通量关系图(b)(直接碰撞模型,据Farnan, 1999; Rios et al., 2000b; Palenik et al., 2003修改;双重叠模型,据Holland and Gottfried, 1955; Weber, 1990, 2000修改)
在过去的70余年里,一系列关于天然、掺Pu和离子辐射锆石蜕晶化作用的研究表明,存有2种辐射损伤累积模型(不同的测试方法),即直接碰撞模型和双重叠模型(图2b)。例如,随着α通量的增加,拉曼半高宽的变化呈近指数关系(Palenik et al., 2003),而X射线衍射参数呈近“S”型曲线关系(Holland and Gottfried, 1955; Weber, 1990, 2000)。因此,对于评估锆石辐射损伤程度最为广泛的拉曼光谱法而言,拉曼半高宽与α通量之间的函数关系显示,直接碰撞模型的描述是合理的(图2b,Palenik et al., 2003)。
2.2 热退火作用
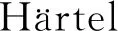
图3 蜕晶质锆石退火趋势峰位值与半高宽关系图(据 et al., 2021b修改;数据引自Geisler, 2002; Pidgeon et al., 2017; Ginster et al., 2019; 范明璞,2020;Ende et al., 2021; et al., 2021b)
3 原理与方法
3.1 锆石拉曼光谱学特征
基于前人对锆石拉曼光谱的研究(Dawson et al., 1971; Nicola and Rutt, 1974; Syme et al., 1977),Nasdala等(1995)指出,理论上,锆石共有12个拉曼振动模式(2A1g+4B1g+B2g+5Eg),以硅氧四面体(SiO4)的振动占据主导位置,且各振动峰的相对强度与激光束的测试方位有关,其原因在于晶体的各向异性。其中,较为明显的7个振动峰包括(图4):3个晶格结构内部振动峰为1008 cm-1、974 cm-1和439 cm-1,分别对应硅氧四面体的反对称伸缩振动B1g(ν3)、对称伸缩振动A1g(ν1)和对称弯曲振动A1g(ν2);另外四个振动峰为202 cm-1、214 cm-1、225 cm-1和356 cm-1,对应于晶格的外部振动,主要是阳离子(Zr4+)的振动引起整个晶胞骨架振动(张成中等,2006)。对于356 cm-1振动峰而言,也有学者将其归于硅氧四面体的内部振动(Dawson et al., 1971)。并且,不同辐射损伤程度锆石的拉曼光谱学特征显示(图4),ν3(SiO4)振动峰最为敏感,也是最能反映辐射损伤程度的特征峰,进而利用该振动峰所对应的半高宽来定量描述锆石的辐射损伤程度(Nasdala et al., 1995, 2001)。一般认为,半高宽是反映锆石晶格结构的有序性,指示硅氧四面体内和硅氧四面体之间键长、键角的规则性变化;峰位值则表征锆石晶格的结晶程度,主要与晶体物质的成分变化和结构缺陷有关,峰位值的漂移代表原子间距增大和晶格扩张(Nasdala et al., 1995, 2003)。

图4 锆石拉曼光谱图(据Nasdala et al., 2001, 2003 修改)
3.2 拉曼光谱的获取与处理
锆石拉曼光谱的精确获取是准确得出ZRDA的关键因素之一,而LRM测试参数的选取和拉曼光谱的处理至关重要。测试参数主要包括:激光波长和能量、物镜倍数、叠加次数、光谱分辨率等。通常,激光能量越高、物镜倍数越高、叠加次数越多,拉曼光谱的信号越强。然而,较高的激光能量可能会改变锆石微区的辐射损伤程度(局部加热),无法获得原始的光谱信息。因此,综合考虑测试精度和效率的背景下,需要先期实验进行测试参数的优化选取。同时,由于锆石晶体的各向异性,在实验过程中,尽可能地保证~1008 cm-1特征峰强度最大处为测试方位。在相同的测试条件下,仪器光谱分辨率可依据测量原子发射谱线所得出的谱峰半高宽来表征,且所测谱线应与待测样品的谱峰(特征峰)相接近。再者,拉曼光谱的处理通常采用分段线性基线校正及洛伦兹—高斯函数(Lorentzian—Gaussian)进行拟合,常用的处理软件包括Wire、PeakFit和LabSpec等,进而对实测半高宽进行校正(公式1,见下文),以消除不同仪器之间的测试偏差,最终得出真实半高宽。
3.3 计算方法
锆石辐射损伤测年方法是利用拉曼半高宽(FWHM)来定量描述锆石所累积的辐射损伤(α通量),结合所测得的U、Th含量,进而得出ZRDA。具体计算方法如下:①利用LRM对锆石~1008 cm-1特征峰对应的半高宽进行测定且对所测得的半高宽进行校正(公式1;Irmer, 1985);②通过所建立的半高宽与α通量的校正曲线计算出锆石所累积的模型通量(公式2;Palenik et al., 2003);③结合U、Th含量(SIMS、EPMA或LA-ICP-MS)及模型通量,依据α通量计算公式得出ZRDA(公式3;Murakami et al., 1991)。
(1)
式中,b为真实半高宽,bs为实测半高宽,s为仪器光谱分辨率。
FWHM=A×[1-exp(-BFWHM·Dα)]
(2)
式中,A是接近最大FWHM值,BFWHM与每个α衰变事件造成的材料损伤质量有关,Dα为等价辐射损伤通量。基于统计学回归分析(R2= 0.975),A值为35.64 cm-1,BFWHM值为5.49×10-19/g。
Dα=8N1·[exp(λ238t-1)]+
7N2·[exp(λ235t-1)]+
6N3·[exp(λ232t-1)]
(3)
式中,N1、N2和N3分别代表现今238U、235U和232Th的分子数,λ238、λ235和λ232代表相应同位素的衰变常数,t为年龄,公式采用现今U的丰度(假设238U = 0.9928,235U = 0.0072)。
4 应用与实例
近年来,随着拉曼光谱定量描述锆石辐射损伤程度这一技术的广泛应用,锆石辐射损伤测年方法作为一种新兴的低温热年代学技术,现已成功应用于判定碎屑锆石物源区(Garver and Davidson, 2015; Resentini et al., 2020)、揭示岩体热演化史(Nasdala et al., 2001; 刘文元和刘景波,2009;Pidgeon, 2014; Pidgeon et al., 2016; Hueck et al., 2018; Anderson et al., 2020)、示踪岩浆锆石的源岩信息(Nasdala et al., 2014)、识别继承锆石来源(Bjerga et al., 2022)以及表征锆石在风化过程中的保存能力(Balan et al., 2001)等领域。同时,辐射损伤的定量评估在校正锆石LA-ICP-MS U-Pb年龄测定的“α通量基体效应”(Allen and Campbell, 2012; Crowley et al., 2014; von Quadt et al., 2014; Solari et al., 2015; Marillo-Sialer et al., 2016; 王家松等,2016;Sliwinski et al., 2017)和指示He扩散行为(提高锆石(U—Th)/He测年精度)(Reiners et al., 2004, 2017; Guenthner et al., 2013; Powell et al., 2016)等方面发挥着重要作用。
4.1 示踪物源区


图5 碎屑锆石多重测年技术物源分析示意图(a)、(b)(据修改)与阿拉斯加地区前寒武纪碎屑锆石“eU”和 ν3(SiO4)振动峰拉曼位移关系图(c)(虚线为不同辐射损伤所对应的等价累积时间,据Garver and Davidson, 2015修改)
值得注意的是,对于一些较老或U含量较高的碎屑锆石而言,通常具有中—高等程度的辐射损伤,当进行裂变径迹和(U—Th)/He年龄计算时存有一定的难度和局限性(如高密度的裂变径迹,子核He的丢失等)。现今,随着人们对锆石蜕晶化和热退火作用的研究进一步加深,结合碎屑锆石所保留的辐射损伤和所经历热退火事件的差异来进一步限定潜在物源区,使得辐射损伤(年龄)在碎屑锆石示踪物源区领域成为一种极具应用潜力的新兴方向和热温度计(Garver and Davidson, 2015; Enkelmann and Garver, 2016; Resentini et al., 2020)。例如,采用拉曼光谱法对阿拉斯加地区的一系列前寒武纪(约1000~2000 Ma)碎屑锆石进行分析,尽管这些锆石的U-Pb年龄具有相似性,但所累积的辐射损伤存有明显差异,表明这些碎屑锆石经历过不同的热演化史,对应的辐射损伤累积等价时间约为500~1000 Ma和100 Ma,从而依据这一特征分辨出这些锆石来自于不同的物源区(图5c)(Garver and Davidson, 2015);同样地,基于该方法对非洲南部Zambezi三角洲地区的物源进行分析,根据锆石拉曼峰位值和所累积α通量之间的关系,划分出三个不同的趋势(未退火、部分退火和高度退火),再依据锆石U-Pb年龄及可能经历的热事件(~1.0,~0.6,~0.26和~0.12 Ga)计算出累积的α通量,进一步区分潜在的物源区(Resentini et al., 2020)。因而,采用锆石拉曼光谱和U-Pb年龄相结合的分析方法可为示踪物源区领域提供一种新的途径,无需特殊制样且测试效率高,便可获得源区的热演化信息。
4.2 揭示岩体热演化史
同位素定年技术在地质学中的应用极为广泛,对于研究与解决地质体的形成时代、变质时代、沉积上、下限时代、构造变形定年、盆山耦合关系和造山带的隆升史与剥露史等方面发挥着极其重要的作用。高温年代学一般代表岩体的形成年龄,而低温年代学则指示岩体的冷却或剥蚀年龄。现今常用的低温热年代学方法有:锆石、磷灰石裂变径迹和(U-Th)/He测年,可应用于重建地壳浅部所经历的热事件等多方面研究(周祖翼,2014;田朋飞等,2020)。而随着锆石辐射损伤测年方法的不断改进和完善,已被认为是一种潜在的低温年代学测试手段。近些年来,该方法在约束和揭示岩体隆升时代及所经历的热事件等相关领域扮演着重要角色(Nasdala et al., 2001; 刘文元和刘景波,2009; Presser et al., 2012; Pidgeon, 2014; Pidgeon et al., 2016; Hueck et al., 2018; Anderson et al., 2020)。
基于初步建立的ZRDA校正曲线,对Ivrea地区的麻粒岩锆石进行测试,得出该岩体自形成之后经历了长期的热退火且在古近纪时期开始隆升(Nasdala et al., 2001);通过对大别山高压—超高压片麻岩锆石进行拉曼光谱分析,指出这些变质锆石所保留的α通量是自~200 Ma以来累积而成,进一步表明超高压岩石在~200 Ma已出露地表,与前人的研究结果基本一致(刘文元和刘景波,2009);对经历过海西(~300 Ma)和阿尔卑斯运动(~35 Ma)两期变质事件的古老基底锆石进行测试,结果表明,其经历过部分退火且表现出明显不同的ZRDA,尽管该年龄并不对应于地质事件的发生时代,但对于理解地质演化过程具有一定的指示意义(Presser et al., 2012);综合已有的黑云母Rb-Sr年龄(约500~380 Ma)和地震、重力场资料,西澳大利亚达令山脉太古代花岗岩体的ZRDA显示,该岩体隆升于~420 Ma(温度低于~320℃)(Pidgeon, 2014);采用相同方法对阿波罗14号样品中锆石进行测定,得出该锆石于~3410 Ma发生过热退火事件且退火温度介于230~500℃,从而推测该岩石的邻区曾产生过大量的熔岩(3150~3750 Ma)(Pidgeon et al., 2016);结合锆石和磷灰石(U—Th)/He年代学结果,Hueck等(2018)对巴西南部地区的地质意义进行探讨,发现ZRDA与锆石(U—Th)/He年龄相比稍微偏大且比较分散,认为尽管锆石辐射损伤的退火机制尚不明确,但ZRDA在一定程度上可反映出该地区经历过不同的热事件;通过对里昂山脉的花岗岩锆石进行分析,结果显示,ZRDA(~560 Ma)与锆石裂变径迹年龄(540~580 Ma)相似,且该年龄与Iapetus洋的打开和Rodinia超大陆裂解后的冷却时期相对应(200~350℃)(Anderson et al., 2020)。综上,对锆石进行ZRDA的测定,一定程度上可以反映岩体隆升时代及所经历的热事件,再结合其他低温年代学方法的研究,便可获得更多的热年代学信息。
4.3 校正LA-ICP-MS U-Pb测年α通量的基体效应
自20世纪80年代,激光(LA)和电感耦合等离子质谱(ICP-MS)技术连用以来,因其具有制样简单、测试迅速、高分辨率并可进行原位分析等优点,已成为锆石U-Pb同位素定年分析的首选对象(Gray, 1985; Liu Xiaoming et al., 2007)。而随着其在地学研究中的应用日趋深入,锆石LA-ICP-MS U-Pb同位素测年的精确度(精密度和准确度)受到研究者们的广泛关注(Black et al., 2004; Allen and Campbell, 2012; Marillo-Sialer et al., 2014, 2016; Steely et al., 2014; von Quadt et al., 2014; Li Xianhua et al., 2015; Solari et al., 2015; 王家松等,2016;Sliwinski et al., 2017; 李献华等,2022)。已有研究表明,所测锆石与标准锆石所保留的辐射损伤(α通量)差异会导致U、Pb同位素剥蚀坑内分馏行为和剥蚀速率的不同(α通量基体效应),从而引起LA-ICP-MS和同位素稀释—热电离质谱(ID-TIMS)U-Pb年龄测试结果存有偏倚,尤其是对于古老或年轻的锆石而言,偏离程度可达约2%~5%(Allen and Campbell, 2012; Marillo-Sialer et al., 2014, 2016)。近年来,随着人们对这一问题的持续关注和重视,许多学者已进行了一些探索并取得较为一致的成果和认识。例如,Allen and Campbell(2012)对13组锆石进行测试,结果表明,所测锆石的LA-ICP-MS和TIMS U-Pb年龄的差异与α通量具有良好的相关性(R2= 0.94),并且认为在锆石进行LA-ICP-MS U-Pb年龄测试之前对标准锆石和所测锆石进行热退火处理可消除二者之间α通量的差异,进而降低测年偏差。但是,该校正公式(年龄差与α通量)并不能推广使用,原因在于该公式是基于结晶年龄所计算的理论α通量(公式3),并不完全对应于实际所保留的α通量(锆石自形成后可能会经历热退火事件);另有研究指出,锆石的辐射损伤程度(α通量)和激光剥蚀坑的深度呈正相关性(Steely et al., 2014);与此同时,相关研究表明,对锆石进行先期的化学磨蚀(chemical abrasion)热退火处理(850~900℃)可提高测年的精确度(Crowley et al., 2014; von Quadt et al., 2014; Solari et al., 2015)。然而,锆石的LA-ICP-MS和TIMS U-Pb年龄差可归因于剥蚀速率的不同,热退火处理并不能完全消除测试样品与标准锆石之间剥蚀速率的差异,对提高测年的精确度是有限的,并且热退火实验需要更高的温度(>1000℃)(Marillo-Sialer et al., 2014, 2016);近期,王家松等(2016)研究表明,结合已有的校正公式(图6a)和拉曼光谱的测试能够实现对α通量的准确校正(图6b);同样地,Sliwinski等(2017)报道了U-Pb年龄不确定性与α通量之间的函数关系,进一步提高锆石U-Pb年龄的测试精度,尤其是新生代以来的锆石。

图6 LA-ICP-MS和TIMS 206Pb/238U年龄差与α通量关系图(a)(据Allen and Campbell, 2012修改,数据引自与α通量校正前后LA-ICP-MS U-Pb年龄对比图(b)(数据引自王家松等,2016)
综上,标准锆石和所测锆石中所保留的辐射损伤(α通量)差异是导致LA-ICP-MS与TIMS U-Pb年龄之间存有偏倚的一个重要因素,而热退火实验可以消除晶格的辐射损伤,从而达到提高测年精确度的目的。但是,在现今年代学发展趋势的背景下(见引言),当对单颗粒锆石进行多重定年(裂变径迹、(U—Th)/He和U-Pb年龄)时,热退火实验处理显然是不可行的,这时就需选择合适的标准锆石(与所测锆石保留的α通量相匹配)或对所测锆石的α通量进行定量化评估。然而,在对未知锆石进行测年时,难以直接获得所测锆石的实际α通量。因此,根据现今年代学的发展需求,对于一些特殊样品展开年代学工作时,选择合适的测试微区进行拉曼光谱和U-Pb年龄的测定,获得锆石所保留的辐射损伤(公式2),再结合α通量—年龄差的校正公式,便可得到较为准确的LA-ICP-MS U-Pb年龄结果。值得一提的是,这一测试流程可同时得到ZRDA,进而获取更多的年代学信息。
4.4 指示He扩散行为
锆石(U—Th)/He热年代学是基于氦同位素(He)的扩散行为发展而来,常被用于研究(近)地壳的热演化过程(Reiners et al., 2004; Enkelmann and Garver, 2016)。研究表明,锆石所累积的辐射损伤会改变He的扩散速率从而间接影响He保留的tc,引起He年龄存在较大的不确定性,即辐射损伤的增加会逐渐阻碍He的扩散,提高保存率,使得tc升高,进而导致He年龄偏大(Reiners et al., 2004, 2017; Guenthner et al., 2013; Powell et al., 2016)。故而,更为详细地评估和理解锆石所累积的辐射损伤(α通量)是精确解释He扩散机制和模拟热演化史的关键所在。Guenthner等(2013)通过一系列高温加热实验探索锆石所保留的辐射损伤对He扩散机制的影响,结果表明,存在不同的扩散模型(图7):一是低等辐射损伤程度时(0.012×1015~1.4×1015α/mg),随着辐射损伤的增加,He扩散系数逐渐减小、tc会增大,锆石的eU与He年龄呈正相关性;二是高等辐射损伤程度时(>2×1015α/mg),He扩散系数随辐射损伤的增加而增大、tc则减小,锆石的eU与He年龄呈负相关性。相应地,综合HeFTy(Ketcham, 2005)和 QTQt热模拟软件(Gallagher, 2012),该模型已成功应用于限定地质体近地表的热演化史(Orme et al., 2016; Guenthner et al., 2017; Johnson et al., 2017)。然而,新近研究指出,基于辐射损伤累积—退火模型得出He的tc推测值和经验值存有差异,而这一差异在一定程度上可归因于辐射损伤(U、Th成分环带)(Powell et al., 2016; Anderson et al., 2017; Johnson et al., 2017)。为此,Anderson等(2020)认为在对锆石进行He年龄测定时,结合拉曼光谱面扫(Raman mapping)分析,识别和量化锆石的辐射损伤程度(或辐射损伤环带),将有助于研究者们更为深刻地理解He扩散机制,从而获得更为精确的年代学结果。
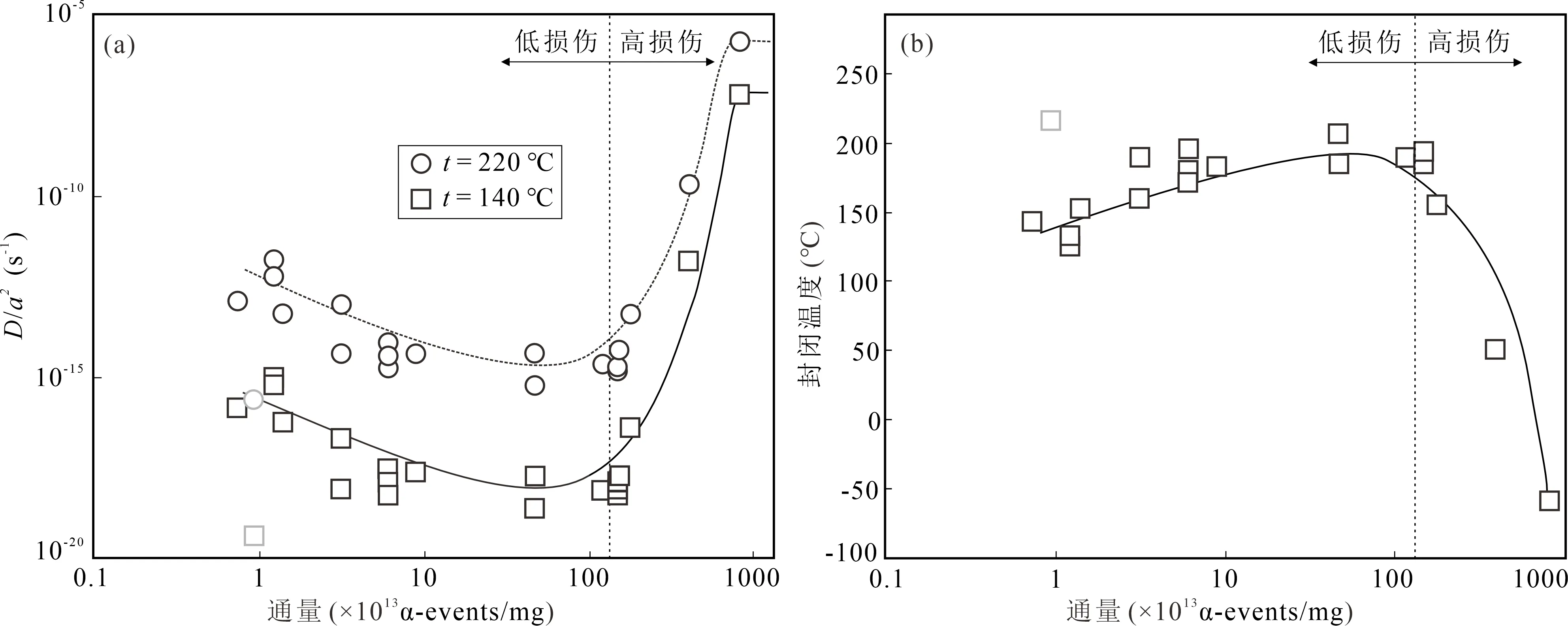
图7 不同温度下(140℃、220℃)锆石中He扩散率(a)和封闭温度(b)与α通量关系图
5 尚存的研究问题

5.1 实验测试的不确定性
研究表明,LRM测定锆石半高宽的不确定性约为±0.1 cm-1(合成锆石),且测试误差与锆石的辐射损伤程度和仪器分辨率等因素有关(Palenik et al., 2003; Anderson et al., 2020; 范明璞,2020)。对于低—中等辐射损伤的锆石而言,半高宽的测试误差可小于±0.5 cm-1(Pidgeon et al., 2016)。LA-ICP-MS测定锆石中U、Th含量时,所引入的偏差因含量的变化而有所差异,在大多数天然锆石中,相对标准偏差可小于3%(图8)。以上结果显示,LRM和LA-ICP-MS的测试误差并非实验测试不确定性的主要来源。一般而言,LA-ICP-MS U-Pb年龄测试的斑束直径为~20 μm时,所对应的测试深度约为20~30 μm,而LRM测试直径为1~2 μm,所对应的测试深度可达30~50 μm(Presser and Glotzbach, 2009)。因此,两种测试仪器分辨率的差异(空间不匹配性)是实验测试不确定性的主要来源。由于多数锆石中U、Th的分布具有不均匀性(辐射损伤的累积密度存有差异),这便要求在测试的过程中,选取合适微区进行拉曼光谱的多次测定,从而尽可能地缩小二者在空间上的不匹配性,即假设同一柱体体积内U、Th含量与半高宽近似匹配(Anderson et al., 2020)。再者,由于锆石中U、Th衰变所产生的α粒子停止、反冲距离分别约为10~30 μm和30~40 nm(Farley et al., 1996),那么在一些高(或低)U、Th成分环带过渡区域必然存在U、Th含量与半高宽的不匹配性(α粒子植入效应),进而影响ZRDA的测试精度。故而,在该方法的推广之际,务必对这一问题加以重视。

图8 锆石U、Th含量与实验测定(LA-ICP-MS)的相对标准偏差(RSD)关系图(数据引自柳小明等,2002)
5.2 校正曲线的不确定性


图9 不同元素含量与半高宽(ν3)变化量关系图(阴影区域为不确定性,数据引自范明璞, 2020)
5.3 封闭温度的不确定性

图10 锆石辐射损伤退火温度图(据 修改)
6 结语与展望
近20年来,随着低温年代学技术的飞速发展与完善,使其逐渐成为研究地壳顶部发生的构造和气候驱动过程相互作用的重要手段,进而获得地表到下地壳多种地质过程的关键信息(田朋飞等,2020;李广伟,2021)。然而,在运用多种测年技术的过程中,仍然存在成本高、效率低、周期长、精度较差、年代学信息单一等问题,这也为低温年代学未来的发展趋势提出了新的要求,即不断改进和优化实验流程、开发新的测年手段、深化联用多种定年技术、探索更为全面的动力学模型等。而锆石辐射损伤测年方法作为一种低温年代学技术,其最大优势在于高效、低成本、无需特殊制样等,尤其是对多颗粒样品的分析,完全契合现阶段年代学测试技术的发展需求。在更多地融入其他低温年代学信息的基础上(裂变径迹和(U—Th)/He 测年),对推动热年代学在地球科学领域的进一步发展和应用具有重大意义。正如本文所述,随着科学研究的不断深入,在未来的研究工作中,对同一锆石颗粒甚至可实现四重定年,即(U—Th)/He年龄、裂变径迹年龄、辐射损伤年龄和U-Pb年龄。同时,基于拉曼光谱对锆石辐射损伤程度的精确描述,可对锆石U-Pb和(U—Th)/He年龄进行校正和约束,进而获得更为丰富、准确的热年代学信息。诚然,锆石辐射损伤年代学在地学研究的应用中尚存一些关键问题:微区测试(分辨率)的不匹配性、封闭温度存有争议、较大的年龄偏差、辐射损伤和退火机制的精确描述等,这必然会影响和阻碍该方法在地学领域中的广泛应用。因此,在今后的研究中,仍需研究者们积极、深入的开展相关工作,改进和完善该方法的不足之处,以期进一步促进地质年代学的发展,解决更多的地质问题。
