考虑预应力的鼓式制动器制动鼓模态分析
2023-02-27何宁张德龙张庆华
何宁,张德龙,张庆华
(741000 甘肃省 天水市 甘肃机电职业技术学院)
0 引言
制动器的固有频率影响整车的舒适性、噪声等[1-2]。在结构的静态、动态分析中利用有限元进行制动器的固有特性分析,可以较快甄别制动器在设计阶段能否满足汽车的制动噪声要求,这样不仅可以缩短试验周期,而且节省试验费用。基于有限元分析软件,本文对鼓式制动器的制动鼓进行预应力模态分析,提取制动鼓前10 阶模态进行固有频率和噪声振动振型分析[3]。目前,汽车制动器一般为机械摩擦式的,利用固定元件与旋转元件两表面间的机械摩擦产生制动力矩,使得车辆减速或驻车。根据制动器在汽车上的位置,其可分为车轮制动器和中央制动器,前者安装在车轮处,后者安装在传动系的某轴上[4-5]。
1 鼓式制动器三维建模
本文所研究的某款轿车鼓式制动器为领从蹄式鼓式制动器,主要结构组成为制动鼓、制动蹄、摩擦片。简化后基于SolidWorks 建立的三维模型如图1 所示,其各部分的几何参数如表1 所示。
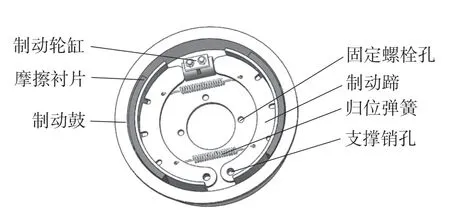
图1 鼓式制动器简图Fig.1 Schematic diagram of drum brake

表1 鼓式制动器结构参数Tab.1 Structural parameters of drum brake
2 鼓式制动器制动鼓模态分析
2.1 结构动力学方程
制动鼓的自振因素较多,其中最重要的是路况不同所带来的伴随着轮毂的冲击,从而产生的共振,直接损伤制动鼓,对整个制动系统的制动性能产生影响[6-8]。模态分析是自由振动分析,是研究结构动力特性的一种近代方法。模态是机械结构的固有特性,每一个模态具有特定的固有特性、阻尼比和模态振型,模态参数可由计算或试验分析取得,这一过程叫做模态分析[9-10]。试验表明,低频模态对机械的影响甚微,所以本文选取制动鼓的前10 阶振型作为分析对象。
制动鼓的动力平衡方程为
式中:[M1]——制动鼓质量矩阵;[C1]——阻尼矩阵;[K1]——刚度矩阵;X(t)——整个结构的位移量;f(t)——制动鼓受到的外部激励向量。
模态分析的对象是一个无阻尼的自由振动系统,其目的是识别出系统的模态参数,为结构的振动特性分析、振动故障诊断和预报、结构动力学特性优化提供依据。
制动鼓的动力平衡方程修正为:
因此在制动鼓的振动模态分析中,物理坐标可以用参数化模态坐标来代替,参数化计算后,解耦后成不相关的独立微分方程。计算的结论表明,物理参数模态化的结果可以解决大型平台的共振分析问题。
2.2 制动鼓边界约束
基于SolidWorks 三维建模软件的鼓式制动器制动鼓简图如图2(a)所示。对制动鼓网格划分采用3D 实体八节点六面体Hex Solid45 单元类型,网格控制选择sizing=5 mm,网格划分效果如图2(b)所示,材料参数见表2。
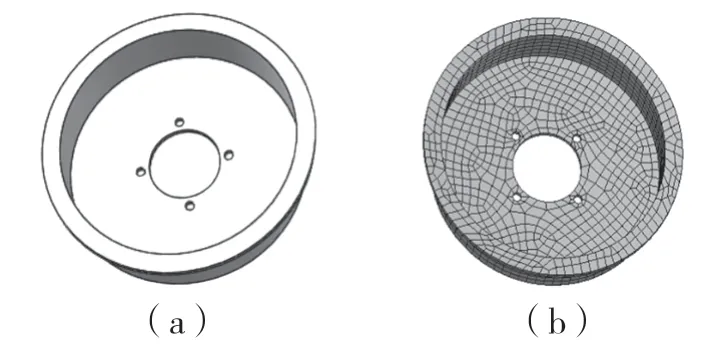
图2 制动鼓及其网格划分图Fig.2 Brake drum and its grid division
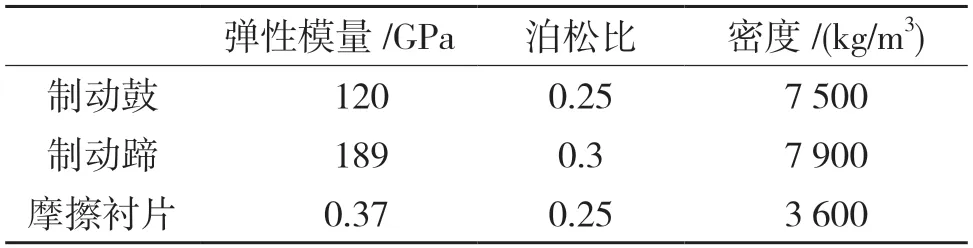
表2 材料特性参数Tab.2 Material property parameters
对制动鼓进行模态分析,不存在结构与热载荷,无须考虑任何的力载荷,只须设置边界约束条件,因为模态分析是纯粹的线性分析。制动鼓模态分析的约束条件为:(1)预应力约束。汽车在行驶中,制动鼓随着车轮一起转动,为了更好地模拟制动鼓的运行情况,考虑在制动鼓的模态分析中加入旋转角速度ω=10 rad/s;(2)将制动鼓的底部螺栓孔内表面设置为固定约束。
2.3 制动鼓模态求解
由于制动鼓受到外界激励的频率较高,而低阶频率又对制动鼓的制动性能起到决定作用,因此本文提取制动鼓的前10 阶模态,如图3 所示。
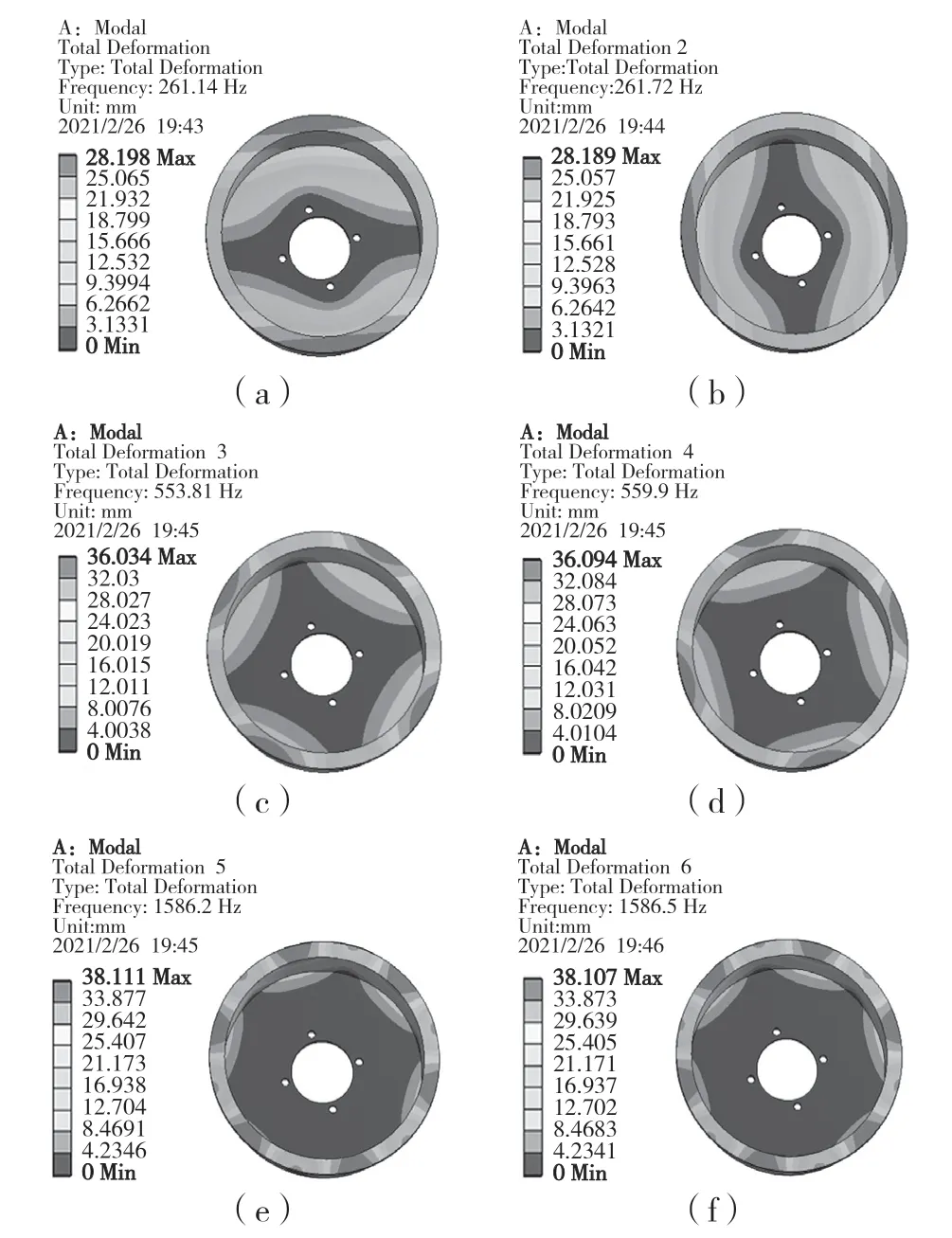

图3 各阶模态振型图Fig.3 Modal shape diagram of each order
2.4 制动鼓振型分析
Block Lanczos 是众多机械结构模态分析常用的方法。鼓式制动器所面临的工况较复杂,除了本身制动促动力的挤压摩擦,本文研究的制动鼓主要考虑了路面工况所带来的冲击,这样就构成了一个多自由度复杂的工况系统,从而使建立的有限元模型也很庞大。采用Block Lanczos 能很好地利用制动鼓某些网格单元存在质量较差的单元模型模拟实际工况,能简化计算,提高效率,得出较准确的分析结果。制动鼓前10 阶模态的固有频率和振型描述如表3 所示。
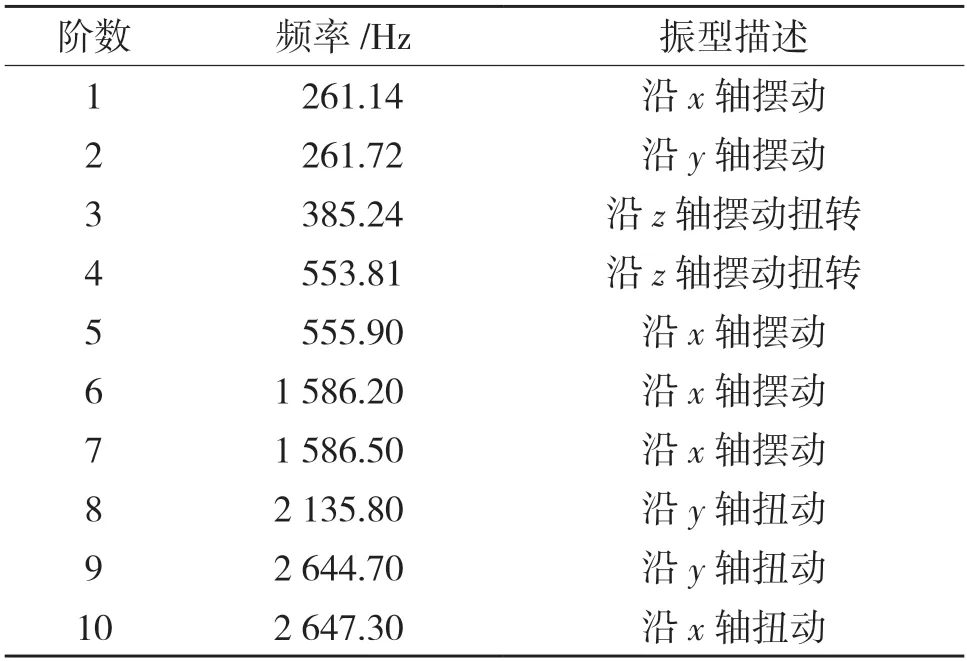
表3 制动鼓固有频率和振型描述Tab.3 Natural frequency and mode description of brake drum
由图3 可知,模态1 阶、2 阶振型基本相同,只有一个相位角的差别,振型主要表现为1 阶摆振,两半圆的位移相差较大。第3 阶和第4 阶的模态振型也是基本相同,只有相位的差别而已,均表现为对称振,振动位移沿直径对称分布。第5 阶、第6阶模态开始表现为圆周振,相位角逐渐减小,且位移沿径向发生扩散变化。第7、第8 阶模态完全为圆周振动,同一半径圆上的位移相同。第9 阶和第10 阶均是表现为3 阶的扭转振动。
根据制动器噪声研究的经验,道路试验时鼓式制动器产生的噪声频率应在800 Hz频程范围内,并且500~1 000 Hz 为制动噪声的主要研究范围。综上分析所得,制动鼓的第5、第6 阶固有频率分别为555.90 Hz 和1 586.20 Hz,接近道路研究的800 Hz 的噪声研究范围,因此满足制动器噪声研究理论。
3 结论
考虑到制动鼓随车轮以一定角速度一起转动,对制动鼓进行预应力的前10 阶模态分析;由噪声振动的经验可知:此鼓式制动器制动鼓的第5、第6 阶固有频率分别为555.90 Hz、1 586.20 Hz,接近道路研究的800 Hz 的噪声研究范围,这些研究为制动器的结构参数和材料参数的设计提供了一定的参考依据。
