基于MSC.Fatigue的链条疲劳寿命分析与优化
2023-02-27付振明李存志谢爱军王桂斌
付振明,李存志,谢爱军,王桂斌
(1.青岛征和工业股份有限公司,山东 青岛 266700;2.中国机械工程学会机械传动分会 链传动专业委员会,长春 130022)
0 引言
疲劳寿命作为链系统性能的重要质量指标,一直以来都是行业内各制造企业所关注的重点,国际标准ISO 606:2015标准中也明确规定了链条必须达到的最小动载强度要求。目前,仅A系列标准滚子链有链条疲劳寿命的近似计算方法,其余系列链条仍然没有明确的参考设计方案可循。通常是按照国际标准ISO 15654:2015进行疲劳寿命的试验验证[1],此方式并未对前期的设计阶段起到直接指导作用,反而导致了设计安全系数预留过剩的问题。本文以ABAQUS有限元分析结果、Miner线性累积损伤理论为基础,利用MSC.Fatigue的全寿命(S-N)分析方法,在设计阶段就可以快速得到产品的疲劳寿命分布情况,避免设计缺陷的产生,大大提高了链系统产品的开发效率,同时为设计过程中的产品优化奠定了基础[2]。
1 研究技术路线
本文以链传动行业所遵循的设计标准为依据,进行某型号链条零件尺寸参数设计,在满足静强度理论分析的基础上,建立三维模型和有限元模型。采用与实际疲劳试验相一致的方法,选取产品疲劳性能设计要求的载荷水平分别进行ABAQUS有限元应力分析。ABAQUS有限元应力结果、材料疲劳特性与载荷谱作为输入进行MSC.Fatigue的全寿命(S-N)分析,确定链条的最小疲劳寿命及其分布,验证链条是否满足疲劳寿命的设计要求,具体研究技术路线如图1所示。
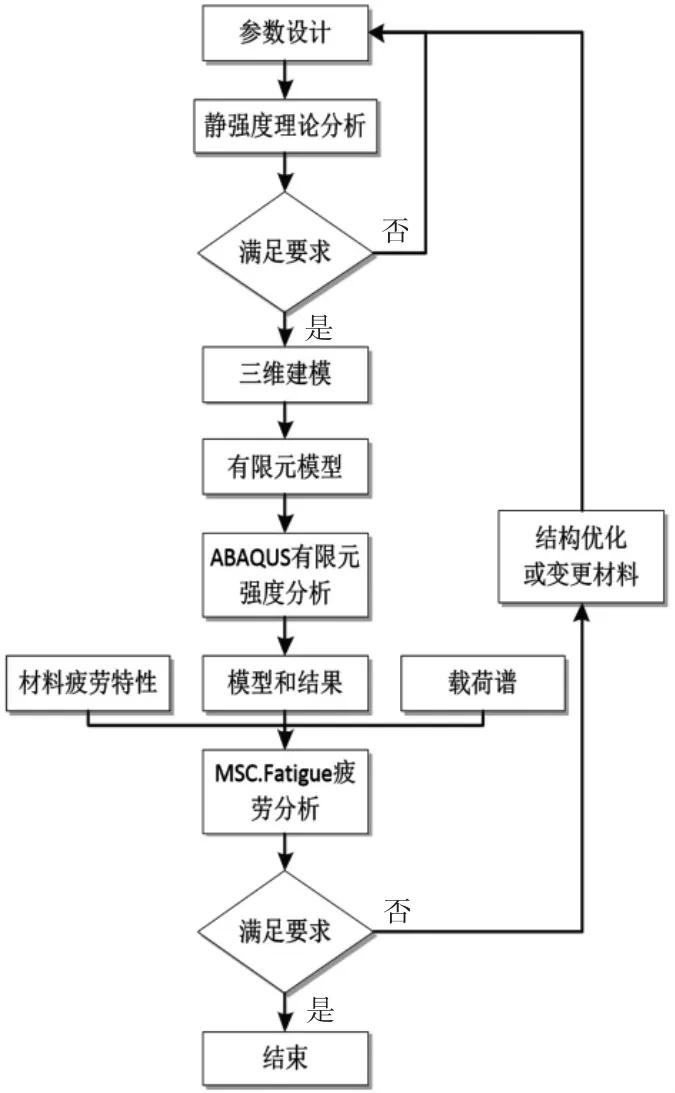
图1 研究技术路线
2 链条零件参数设计与静强度理论分析
以64B(4 in) 链条为分析对象,依据国际标准ISO 606:2015 进行各零件尺寸、材质等关键参数的设计,如表1所示。

表1 零件参数表 mm
链板拉伸强度校验公式[3]为
式中:Fumin为链条最小抗拉强度,取1120 kN;t为链板厚度;h为链板高度;d为链板孔径;σb为材料抗拉强度,取1080 MPa;d2为销轴直径;τ为材料抗剪强度,取784 MPa。
由式(1)、式(2)可得,内外链板的拉伸强度σ内、σ外分别为1025.9、1006.2 MPa,均小于许用抗拉强度要求。销轴的剪切强度τ为506.3 MPa,也小于许用抗剪强度要求。
通过理论校验可以看出链板抗拉强度、销轴抗剪强度均满足许用强度要求,尺寸、材质等参数设计可行,后续的疲劳样件模型则在上述参数的基础上建立。
3 ABAQUS有限元分析
3.1 有限元模型建立
为提高模型的分析效率,对整个疲劳分析模型进行简化,模型仅包含3个链节和两端夹具。由于滚子零件不会对链条的疲劳寿命产生影响,也将其省略。在ABAQUS中使用C3D8R网格类型的六面体网格对模型中各零件进行划分,如图2所示。
模型的边界条件如图2 所示,分析工况按照国际标准ISO 15654:2015进行。由于考虑到疲劳设计的安全系数,一般载荷水平以通过标准之上的3级载荷水平且循环次数达到3×106作为链条疲劳强度是否满足要求的判定标准。模型一端固定,另一端按照特定载荷进行水平轴向加载。所加载载荷选取载荷水平中对应的最大载荷Fmax作为有限元的分析工况,按照步长累加的升降法原则[4-5]持续分析4个载荷水平下的应力结果,以便得出循环次数达到3×106的载荷水平,判定是否达到疲劳设计要求。仿真开始的动载强度Ft按照标准取107 kN,步长取11 kN。其中载荷水平如表2所示。
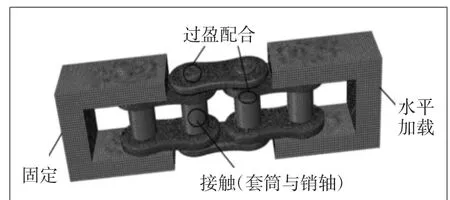
图2 链条疲劳分析FEM模型及边界条件

表2 载荷水平
3.2 链条应力分析
分别在4级载荷水平下,利用ABAQUS进行应力求解,得出链条应力云图,如图3所示。通过应力云图可以看出,疲劳链段在不同载荷水平下,最大应力位置均出现在内链板内孔 区 域[6],这 与实际应用中链条经常出现裂纹的位置相符[7],并且最大应力随着载荷水平的提高而不断增加。当最大载荷为159.6 kN时,最大应力为482 MPa。另外,从应力云图也可以看出各零件所受应力均低于屈服强度,可以用于后续的MSC.Fatigue 的全寿命(S-N)仿真分析。由于套筒和销轴两种零件所受应力远远低于疲劳极限所限定的应力值,实际应用中也不存在疲劳损伤的情况,在此不再进行过多的分析。

图3 链条应力云图
4 MSC.Fatigue全寿命(S-N)分析
4.1 Miner线性累积损伤原理
Miner线性累积损伤法则基于损伤积累与循环次数成线性关系的假设前提下,疲劳损伤线性累加,当达到疲劳寿命所限定的某一数值时,构件则产生疲劳破坏[8-10]。
在某一应力水平σ1加载下,构件的疲劳寿命为N,则进行n个循环造成的损伤计算公式为

在σ1、σ2、σ3……σl等l个不同应力水平下(各应力水平对应的疲劳寿命依次为N1、N2、N3……Nl),则各应力水平进行n1、n2…、nl次循环,造成的损伤为

当损伤累积之和D等于1时,构件将会发生疲劳破坏[11]。MSC.Fatigue的全寿命(S-N)则是基于该理论进行仿真计算。
4.2 疲劳载荷谱及材料的S-N曲线
构件的疲劳寿命主要取决于其力学性能的优劣和载荷水平的高低,合理材料参数和载荷曲线的输入是保证MSC.fatigue计算结果准确的重要因素。国际标准ISO 15654:2015规定了链条疲劳试验时,在特定的频率下,最大载荷Fmax需以正弦方式平滑过渡到最小载荷Fmin[12],并且两者的取值按照式(5)确定:
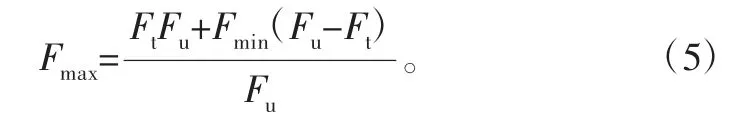
由式(5)可得不同载荷水平下对应的载荷曲线如图4所示。

图4 不同载荷水平的载荷曲线
由于MSC.fatigue中材料数据库中缺少40Cr材料相关数据。因此,需要根据材料在指定存活率的疲劳寿命属性,得出材料对应的S-N曲线表达式[13-15]。40Cr材料在存活率95%下的S-N曲线表达式为
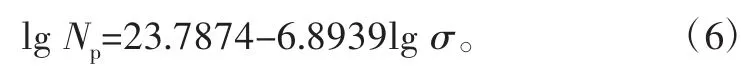
应力幅SRI1、第一疲劳强度指数b1等参数便可由式(6) 得出,对应的40Cr材料S-N曲线如图5所示。

图5 40Cr材料S-N曲线
4.3 疲劳寿命分析与优化
ABAQUS静力学分析结果、疲劳载荷谱及材料的S-N曲线作为MSC.Fatigue的全寿命(S-N)分析的输入,运用Goodman平均应力修正方法,进行疲劳寿命的计算,疲劳寿命结果数据表如表3所示。计算结果仅顺利通过了第1级载荷水平,第2级载荷水平下的疲劳寿命只有4.97×105次循环,显然不满足疲劳设计要求。
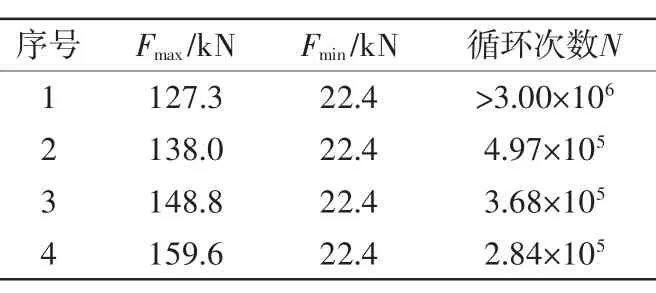
表3 不同载荷水平的疲劳寿命
通过第2级载荷水平下的寿命云图(如图6),可以看出最小疲劳寿命位置与有限元分析结果相同,均处于内链板内孔区域,其余零件均未出现疲劳损伤。为达到疲劳设计要求,必须对链条进行优化调整。
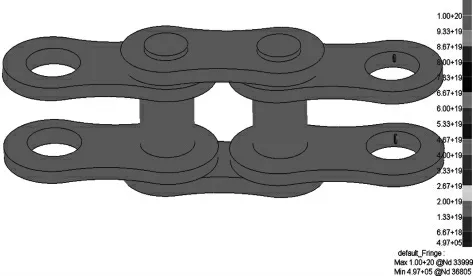
图6 第2级载荷水平的寿命云图
以减小链条整体结构的变动,满足通用性要求为方向,优化方案不再进行结构上的调整,而将链板材质由40Cr变更为42CrMo,两种不同材料的S-N曲线对比如图7所示。变更材质后,再次进行寿命分析,不同载荷水平的疲劳寿命结果如表4所示。

图7 缆筐整体吊装设计

图7 不同材料S-N曲线
由表4可以看出,优化后的链条在第七级载荷水平下发生疲劳损坏,循环次数为2.85×105,第七级载荷水平下的寿命云图如图8所示,最小疲劳寿命位置处于内链板内孔区域,外链板也开始出现损伤,疲劳破坏的最大载荷由138.0 kN提高到191.9 kN,其余6级载荷水平均顺利通过,满足了国标标准以上3级载荷水平且循环次数大于3×106的设计要求。

图8 第7级载荷水平的局部寿命云图

表4 优化后不同载荷水平的疲劳寿命
5 试验验证
为验证上述计算、分析和优化方法的可行性和有效性,将优化设计后的链条做出样品进行疲劳试验验证。验证设备选用PWSE200疲劳试验机, 试验方法按国际标准ISO 15654:2015执行,并采用与分析优化相同的载荷水平和加载方式,在频率为10 Hz条件下进行疲劳试验,如图9所示。

图9 疲劳试验
试验结果:在第七级载荷水平下经过3.25×105次循环后,链条产生疲劳断裂,如图10所示。疲劳断裂零件损伤位置及其循环次数与计算分析结果基本一致,这证明了MSC.Fatigue疲劳寿命分析与优化方法是可行和有效的。
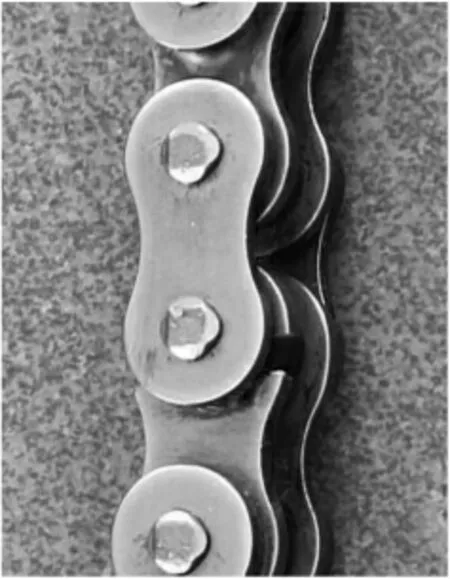
图10 疲劳试验结果
6 结论
1)基于ABAQUS建立了链条疲劳试验模型,并提出了一种基于MSC.Fatigue的链条疲劳寿命分析方法,在链条设计开发阶段就能快速准确确定链条的最小疲劳寿命,缩短了新产品开发周期。
2)通过疲劳试验设备验证基于MSC.Fatigue的链条疲劳寿命分析优化的结果,其结果是一致的,证明了该种基于MSC.Fatigue的链条疲劳寿命分析方法是可行和有效的,为链系统的可靠性设计提供了一个新的技术方案。
