模型与数据双驱动的锂电池状态精准估计

陈清炀，何映晖，余官定，刘铭扬，徐 翀，李振明

（1浙江大学信息与电子工程学院，浙江 杭州 310058；2中国电力科学研究院有限公司储能与电工新技术研究所，北京 100192）

锂电池由于具有循环寿命相对长、自放电量较少、无记忆性问题等优势，对我国新能源的发展与普及具有重要意义。根据中关村储能产业技术联盟全球储能项目数据库的调研报告，截至2019 年6 月，全球采用锂离子或动力电池的储能项目的比重已经超过了总电化学储能的86%[1]。随着锂电池的大面积普及，其本身的性能、利用率及安全性成为了业界最为关注的重点之一。

健康状况(state of health，SOH)、荷电状况(state of charge，SOC)、开路电压(open circuit voltage，OCV)是用于判断锂电池状态是否正常的主要参数。值得注意的是，SOC 无法直接检测，它与可被测得的电池参数(包括开路电压、工作电流、电池内部温度等)间不存在线性关系，所以对于锂离子电池中SOC 值的精确预测是业界研究的主要难点之一[2-3]。

如今较为常见的电池SOC 估测算法可分为直接估计法、模型驱动法与数据驱动法三类。直接估计法包括库仑计数法和开路电压法极易受到环境噪声和测量限制的影响，实用性较差[4-7]。相较于此，现有较为优越的两类SOC 估测方法——模型驱动法和数据驱动法在稳定性、收敛性和预测精度上都有了显著的提高。模型驱动法以卡尔曼滤波[8]为代表，在一定程度上降低了系统的开环风险，但若仅使用模型驱动法，电池模型本身的不精确性会大大影响SOC 估算的精确度，同时电池充放电状态在使用过程中充满随机性，观测量的频繁突变进一步放大了模型驱动法的不稳定性。数据驱动法以神经网络、模糊逻辑[9-10]为代表，在简化电池建模过程的同时保证了算法鲁棒性，但其忽略了系统的开环风险，对于选用的电池状态参数类别、数量、训练方式等都有着极高的要求，因此需要较高的训练成本才能确保其收敛性。

现有的大多数SOC 估测方法采用了模型驱动与数据驱动中的一种，通过将基本的卡尔曼滤波器或神经网络不断复杂化以实现个别算法指标的改进，却无法综合提升算法的估计精度、收敛性、鲁棒性、模型泛化和其他指标方面的全面性能。因此，针对以往算法的片面性，本工作提出了基于模型与数据双驱动的SOC 估测算法，实现了算法综合性能的提高。

本工作主要贡献如下：

（1）明确采用模型驱动与数据驱动的串联融合，在保证精度的同时提升算法的鲁棒性；

（2）创新采用扩展卡尔曼滤波器与无迹卡尔曼滤波器这一组合分别处理SOC 估计中线性程度不同的部分，提升模型驱动法结果的可信度；

（3）使用LSTM 神经网络完成数据驱动法部分，以贴合电池状态具有时序性的特点。

在完成算法设计与搭建后，本工作采用来自NASA卓越中心的电池数据集对单驱动法、双驱动法分别进行测试，以证实双驱动法的优越性。

1 锂电池等效模型

由于本工作算法涉及模型驱动模块，因此需提前建立锂电池等效模型，其精度会极大地影响模型驱动法的性能。

电池等效模型通常可分为电化学模型和等效电路模型两类。通常，电化学模型在模拟电池状态时比后者更精确，然而实操难度较大。与传统电化学模型相比，等效电路模型简单，性能良好。因此，它被认为是最适合估算SOC 的模型之一[11]。N 阶RC 模式也是最常见的等效电路模式之一，具有精度高等优点。它有n个电阻-电容分支，每个分支由一个电阻器和一个电容器组成。然而在实际的仿真模拟过程中，对等效电路模型中无限的RC 网络进行计算分析是不现实的，简化模型是必要的。科研人员对一阶到四阶的RC 等效电路模型进行了仿真试验[12]，发现一阶模型的拟合误差明显较大，而二、三和四阶模型误差相差不大。其原因可能是电池内部的电化学反应随着电池老化越来越复杂，简单的一阶模型已经难以拟合，而高阶模型对复杂的非线性过程有更好的拟合能力。为了便于实际计算，本工作将以二阶RC 等效电路模型为例进行分析。

二阶RC 等效电路模型结构如图1 所示，本工作假设两个RC 并联网络两端的电压差分别为U1、U2。

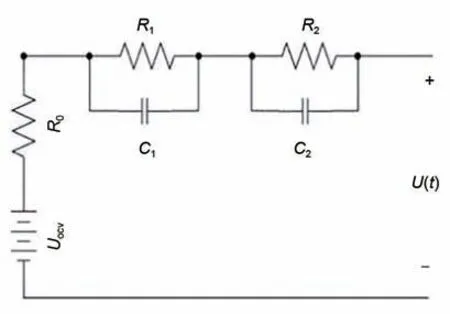
图1 2-RC电池等效模型Fig. 1 2-RC electric equivalent circuit model of battery

2 模型与数据双驱动的SOC 估测算法

2.1 算法流程

2.1.1 双驱动联合模式

由于本研究中电池模型并不精确，相关参数确切简洁，需同时追求估测的实时性和准确性，因此采用较为灵活的串联法来实现双驱动集成。

模型与数据双驱动的联合模式主要可分为串联法、并联法与融合法三种[13]。本工作采取的串联法流程如图2所示，其先后利用两种驱动方式对数据进行处理，输出最终结果。在实际应用过程中，也可以使用模型驱动方式为数据驱动方法筛选关键特性，这样就可以降低数据驱动方法的输入特性维度。数据驱动方法也可用作模型驱动方法的误差校正方法。该方法可以提高准确性、时间效率和灵活性。

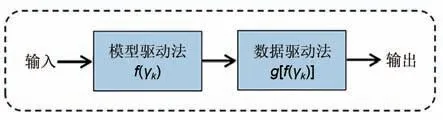
图2 串联法流程示意图Fig. 2 Schematic diagram of serial integration approach

2.1.2 双驱动SOC估测算法流程

首先利用模型驱动模块对电池数据进行处理输出大致的SOC 估计结果，再将该结果及原始数据输入数据驱动模块实现误差修正输出最终结果。

利用SOC 的初步估测数据以及两个卡尔曼滤波器的观测误差值，神经网络可以拟合出初步数据、误差值与最终参考值之间的某种非线性拟合关系，从而实现对初步数据的误差纠正，使其更接近真实值。另外，LSTM神经网络中加入了温度这一特征，从而涉及到了模型驱动法中并没有计算到的部分，更有利于精度的提升。

总体算法流程如图3所示。

图3 双驱动算法流程图Fig. 3 Schematic diagram of dual-driven algorithm

2.2 模型驱动模块

2.2.1 扩展卡尔曼滤波器

锂电池模型是一个经典的非线性系统，然而传统的卡尔曼滤波器仅能用来解决线性问题，无法应对锂电池SOC 这一非线性相关的特征，因此本工作使用到扩展卡尔曼滤波器[14]。扩展卡尔曼滤波器(extended kalman filter，EKF)广泛应用于非线性系统的预判。EKF的基本原理是对状态函数和测量函数执行一阶的泰勒展开，从而使得其局部线性化。对于非线性系统，可以使用以下状态空间方程来描述：

式中，Xk是系统状态变量；yk是系统观测变量；uk是系统输入变量；f是状态的非线性函数；h是观测的非线性函数；wk-1和vk分别是均值为零和协方差为Q和R的高斯白噪声。

在使用EKF估计状态时，需要提供精准的先验噪声统计结果，包括过程噪声方差矩阵Q和测量噪声方差矩阵R。不准确的Q与R会导致EKF的计算准确度降低。如果Q和R太小，不确定性范围将太小，从而导致估计有偏差。如果Q和R太大，可能会导致过滤器发散。另外，EKF 假设Q和R为常数，而在实际滤波过程中，电池模型会受到干扰。此时，应估计模型扰动后的Q与R的值，然后调整滤波器增益矩阵K。

2.2.2 无迹卡尔曼滤波器

无迹卡尔曼滤波器[15](unscented kalman filter，UKF)是典型的通过无迹变换进行递归状态估计的滤波方法。无迹变换方法既可通过几个已知的Sigma 点捕捉Gaussian 分布的均值和方差，还可在使用基于传播的Sigma点的非线性系统的同时捕捉随机变量的后验分布。UKF算法使用一组特定样本的近似概率密度分布，从而拟合状态的后验概率密度，不需要计算Jacobi 矩阵。因此，UKF 不会与EKF一样在强非线性系统中增加估计误差，导致估计精度不理想。

2.2.3 基于双卡尔曼滤波器的模型驱动模块

电池开路电压OCV 指电池在不连入电路情况下正负极之间的电压大小。研究人员证实，在电池开关压力和电池荷电状态之间具有一个稳定的参数关联，而且这个参数关联并不因为锂电池的使用而改变。因此，在已知OCV-SOC曲线的情况下，只需获得OCV即可粗略确认电池的荷电状态。

因此，选择[U1U2SOC]T作为UKF的状态向量，根据2-RC 等效电路以及戴维南定理列出以下方程组：

式中，Cs表示电池在满电情况下可存储的电量，η代表库仑效率，即在相同的充放电的循环中该电池释放的电量与输入的电量的比值。联立方程组并离散化后可得到如下UKF状态转移方程：

式中，X为状态向量[U1U2SOC]T；为与电压U区分，此处系统输入(即k-1 时刻的电流大小)由Ik-1表示。A表示系统状态向量，B表示系统输入的系数矩阵，具体数值为：

式中，τ1、τ2为2-RC电路中两个阻容并联结构的时间常数。

将电池正负极两端电压差作为系统观测量，则锂电池的观测方程为：

式中，UOCV(SOCk)表示由SOC 映射至OCV的函数关系。设[R0]为EKF 的状态向量。由于数据采集频率较高，可忽略锂电池内阻的变化，因此EKF的状态转移方程为

同样将电池正负极电压差作为EKF观测量，观测方程与前文一致。

基于双卡尔曼滤波器的模型驱动算法具体流程如图4所示。

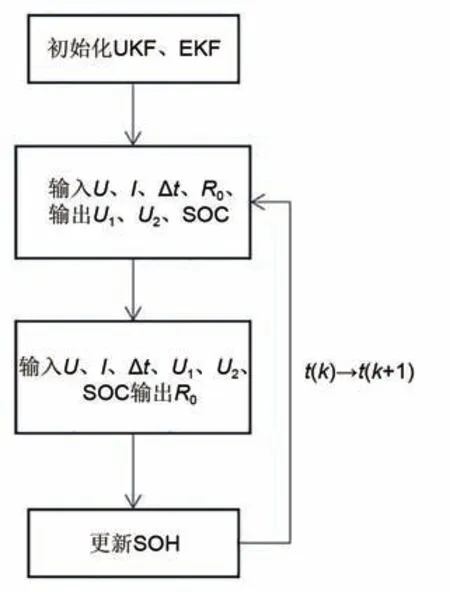
图4 双卡尔曼滤波器算法流程图Fig. 4 Schematic diagram of dual-Kalman filter algorithm

在初始化卡尔曼滤波器后，可通过UKF 对电池的荷电状态和极化电压进行预测，并将此结果作为EKF 的输入，以更新对电池内阻的估计。在EKF算法完成后更新电池满电状态下的电荷量Cs。因为电池SOH 值与电池内部阻抗间具有一一对应关系，因此可利用电池内部阻抗计算SOH，具体表达式如下：

得到SOH 后可根据其定义以及电池生产时的满电状态下储存的电量计算得出Cs，完成一个计算周期。再次采样获得数据后，不断循环上述步骤，从而实现对锂电池各个状态参数的实时估算。

2.3 数据驱动模块

2.3.1 LSTM神经网络

循环归神经网络(recurrent neural network，RNN)的实际训练流程中，由于同时添加了一系列数据，来自早期时刻的信息对当前时刻的输出几乎没有影响。另外，RNN 的一个缺陷就是序列中稳定性的显著降低，在反向扩散过程中很容易发生梯度消失或梯度爆炸。作为RNN的改进版本，LSTM被引入来解决该问题。

图5显示了常用的单个LSTM单元，其中σ表示Sigmoid激活函数，tanh表示双曲函数；Xk是一个1×6 的向量，是整个网络的输入值，包含了第k步时电池的电压、电流、温度、双滤波器观测误差、初步SOC 估计值；hk-1为前一时间步k-1 的输出，即对锂电池SOC 的最终估计值。与RNN 不同，LSTM 配备了三个门来存储长期依赖关系。输入门、输出门和遗忘门组合在一起，以决定一个单元是否应该记忆或遗忘新获取的信息。具体表达公式如式（9）。

图5 LSTM神经网络神经元结构图Fig. 5 Schematic diagram of LSTM neural network

式中，W表示权重，i、f、o和c表示进入门、出口门、遗忘门和记忆单元。b代表偏置。Sigmoid函数的门输出值在0～1之间，但一旦门的值接近于零，将不是存储了新的输入信号(对于输入门)，而是忘记以前的记忆(对于遗忘门)，并且过去的记忆不会影响当前输出(对于输出门)。如图5所示，每个门层实际上都是一个全连接层。LSTM单元的其他部分使用tanh函数作为激活函数，因为它的二阶导数在归零之前可以在很长的范围内保持，这可以有效地解决梯度消失问题。

2.3.2 基于LSTM神经网络的数据驱动模块

长短期记忆神经网络，简称LSTM 神经网络，它具有所有RNN 神经网络都拥有的记忆能力，同时额外配备了遗忘门、输入门和输出门来实现对过去记忆的筛选功能，使其克服了传统RNN 神经网络的长期依赖问题[16]。电池状态是随着时间连续发展变化的，因此在对其进行估计时不仅需考虑当前时刻的各参数值，还需考虑在过去时刻中所测量到的所有性能状态。因此具有记忆功能的RNN 神经网络有着相较于其他数据驱动方法独一无二的优越性，而LSTM 更是RNN 神经网络中性能最为良好的算法之一。

根据采集到的电池运行状态如电压、电流、温度以及由数据驱动法得出的SOC 初步估计值、观测误差、电池SOH 信息构造出符合时序特征的输入数据格式，输入数据是大小为一行六列的矩阵，一行指一个时刻，六列分别指六个电池特征。在利用历史时间信息的形式输入电池特性信息的同时，也将当前时间内特定形式的电池特性信息导入至LSTM神经网络，最后计算得到对锂电池当前荷电状态的估算值。LSTM神经网络的训练结构见图6，首先通过激活函数为Sigmoid 的LSTM 网络，而后进入遗忘率为0.5的dropout层、LSTM学习层、再一次dropout 层之后连入全连接网络并最终输出SOC 估计结果。将每一组训练数据分别代入神经网络模型并不断迭代训练，得到最终的LSTM 模型，输出最终的SOC估测结果。

图6 LSTM模型训练过程Fig. 6 The training process of LSTM neural network

3 实验

3.1 参数获取

本实验的测试数据来自美国国家航空航天局卓越预报中心的电池测试数据集[17]。其中记录了四组锂电池在限定电流大小情况下执行特定的充放电操作。充放电操作共分为随机游走模式(random walk，RW)、参考充放电、脉冲充放电(pulse)、低电流放电。电池中设有传感器以一定频率测量电池的电压、电流、温度、充放电持续时间、充放电模式等信息。

建立电池物理模型后，有部分参数需要提前计算获取以确保后续算法的运行。获得参数的精度会极大地影响算法的准确性。

首先是OCV-SOC对应曲线。目前常用的拟合方法包括复合模型法、多项式拟合法等。传统精确测量电池开路电压的方法要求电池在放电后长时间静置以消除电池内部极化效应产生的压降。该方法效率极低，采样一组数据便需要几个小时的时间。由于锂电池内阻较小，可采用小电流放电的方式来辅助确认OCV-SOC曲线，在同样耗时的情况下可采集多组开路电压数据，此时电池内部的压降为毫伏级别，在大多应用场景中可忽略不计。因此，利用小电流法拟合的OCV-SOC关系曲线如图7所示。

图7 小电流法OCV-SOC对应曲线Fig. 7 OCV-SOC corresponding curve

除此之外，面对非线性拟合问题，采用神经网络更不失为一种更好的选择。本实验使用了传统的BP神经网络实现拟合。神经网络拟合结果，如图8所示。

图8 BP神经网络拟合OCV-SOC对应曲线Fig. 8 OCV-SOC corresponding curve

其次是电池2-RC 等效电路模型的相关参数，包括两个RC 并联网络的时间常数τ1、τ2以及极化电阻R1、R2。已知测试用锂电池脉冲放电曲线如图9所示，且满足以下等式：

利用最小二乘法将涉及数据代入方程可计算得到所需模型参数。

上述参数以及电池欧姆内阻R0、库仑效率η的结果汇总如表1所示。

表1 电池模型参数数据汇总Table 1 Parameters of equivalent model of battery

3.2 恒电流脉冲放电数据测试

本工作利用恒流脉冲放电与随机充放电两组数据分别对单模型驱动法以及模型-数据双驱动进行了测试。为避免电池在长期充放电后SOH 变化带来的误差，本实验选择在完成参考充放电测量后最邻近的Pulse类型数据和Random walk数据进行测试。利用参考充放电数据获得电池当前满电状态下可储存的电荷量Cs，并使用式(12)所示的安时积分法，代入Pulse 阶段的测试数据从而得出实际SOC，为后续估计提供参考。

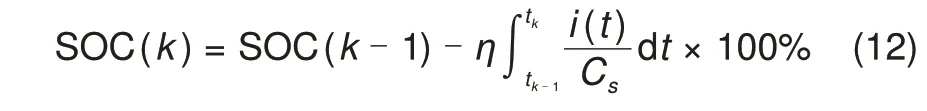
首先使用脉冲充放电数据对算法进行实验。该阶段数据采样间隔为1 s，共20000个数据。分别使用双驱动法、模型驱动法、数据驱动法对SOC进行预测，其中由模型驱动模块得到的双卡尔曼滤波器观测误差如图9 所示，预测绝对误差结果如图10、图11 所示。可以发现，单纯使用模型驱动模块在SOC 值较大时能得到较为满意的结果，估测绝对误差保持在±0.01以内，相对误差保持在±3%左右。在SOC小于0.4后，估测误差会大幅上升，相对误差在0.02 左右。单纯使用数据驱动法对SOC 的估测效果不佳，不论SOC大小如何，误差在均±0.15以上，原因是数据特征较少，神经网络的训练结果难以收敛。双驱动法在精确度上相较于两者均有较为明显的提升，在SOC 较大的情况下，误差可维持在±0.005 以内；在SOC 较小的情况下，通过神经网络的误差纠正，误差也可维持在±0.01左右。

图9 卡尔曼滤波器观测误差Fig. 9 Absolute error of observations of Kalman filters

图10 恒电流充放电SOC估测绝对误差(SOC>0.4)Fig. 10 Pulse charge SOC estimation absolute error(SOC>0.4)

图11 恒电流充放电SOC估测绝对误差(SOC<0.4)Fig. 11 Pulse charge SOC estimation absolute error(SOC<0.4)

以上对恒电流脉冲充放电数据集的估测结果汇总如表2所示，误差CDF分布情况如图12所示。

表2 恒电流充放电SOC估测误差Table 2 Pulse charge SOC estimation error

3.3 随机游走充放电数据测试

首先单纯利用模型驱动模块对随机充放电数据进行预测。数据采样间隔为1 s，共24000 个数据。分别使用双驱动法、模型驱动法、数据驱动法对SOC 进行预测，预测绝对误差结果如图12、图13所示。模型驱动法的SOC估测绝对误差维持在±0.02，在SOH 大于0.4 时，相对误差保持在5%～7%，当SOH 小于0.4 后误差会大幅度上升，相对误差甚会达到0.02+。由以上数据可发现，Random walk阶段的模型驱动法估测精度以及鲁棒性较差，说明了单模型驱动法易受突变因素影响而不稳定的特点。单纯使用数据驱动法对SOC 的估测效果不佳，不论SOC大小如何，误差均在±0.15以上，原因为数据特征较少，神经训练结果难以收敛。

图12 恒电流充放电SOC估测绝对误差概率分布图Fig. 12 CDF of pulse charge SOC estimation absolute error

图13 随机充放电SOC估测绝对误差(SOC>0.4)Fig. 13 Random walk SOC estimation absolute error(SOC>0.4)

图14 随机充放电SOC估测绝对误差(SOC<0.4)Fig. 14 Random walk SOC estimation absolute error(SOC<0.4)

当SOC<0.4 时，双驱动法的相对误差也会有所上升，但绝对误差维持在±0.015以内，相较单驱动法也有所提升。说明在模型和数据驱动的相辅相成下，模型驱动法帮助数据驱动法更好地收敛，降低了数据依赖性；数据驱动法帮助模型驱动法修正了误差，提高了算法总体的鲁棒性。

以上对随机游走充放电数据集的估测结果汇总如表3所示，误差CDF分布情况如图15所示。

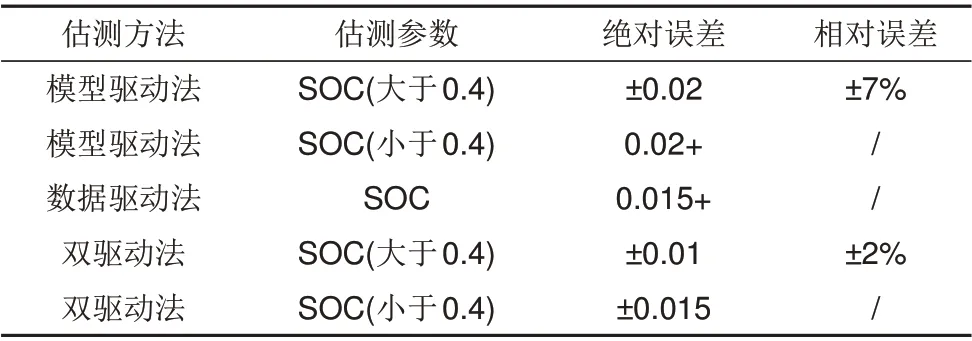
表3 随机充放电SOC估测误差Table 3 Random walk SOC estimation error

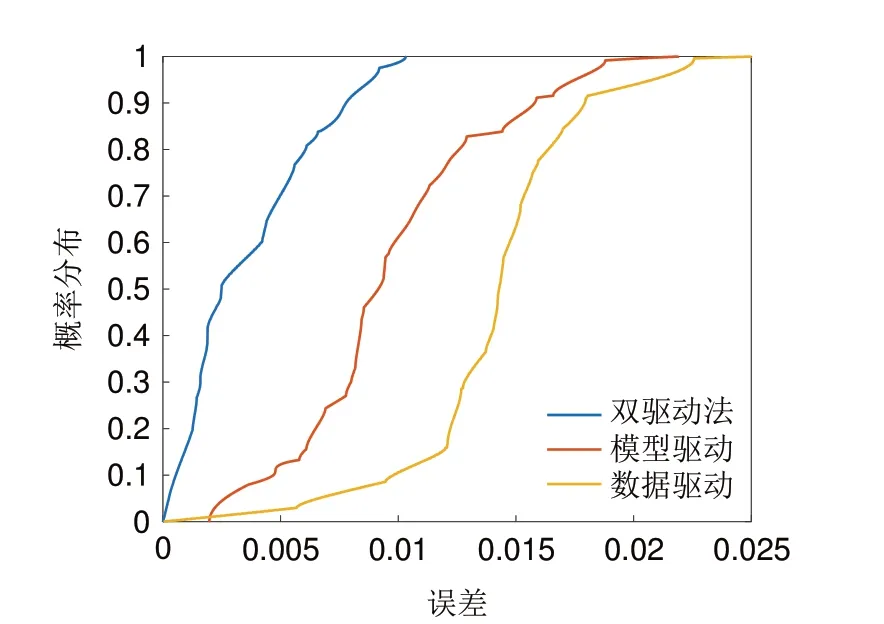
图15 随机充放电SOC估测绝对误差概率分布图Fig. 15 CDF of random walk SOC estimation absolute error

4 结 论

本工作首先讨论了传统SOC 估测方法，总结提炼出了模型驱动法与数据驱动法的优劣并进行了有机结合，通过串联使用的方式得到了一种模型与数据双驱动的SOC 估测方式。实验结果表明，新算法在提高模型驱动法精度的同时降低了数据驱动法对于数据的依赖，相较于单模型驱动法，单数据驱动法具有更高的精确度以及算法鲁棒性。双驱动融合算法具有较高的研究价值，本工作仅探讨了串联使用模型驱动法与数据驱动法的方式来估测电池健康状况。倘若能建立更加精准的电池等效电路模型，融合使用双驱动法不失为一种值得考虑的选择。最后，目前电池爆炸事故频发，为避免类似悲剧的发生，仅仅预测电池SOC、SOH 是远远不够的。BMS需要搭载更多电池健康参数的预测系统，例如电池压力、电池内化学离子浓度、泄漏气体浓度等，从而起到更好的预警作用。