飞轮储能辅助风电一次调频仿真分析
2023-02-27陈俊涛王亚军宋顺一曲文浩柳亦兵
陈俊涛,王亚军,宋顺一,曲文浩,柳亦兵
(1华北电力大学先进飞轮储能技术研究中心,北京 102206;2深能南京能源控股有限公司,江苏 南京 210000)
我国为了积极实现“碳达峰、碳中和”的目标,提出要构建以新能源为主的新型电力系统,推动能源电力低碳转型发展[1]。在新能源的快速发展中,清洁无污染、分布广泛、可再生的风能越来越受到人们的重视,截止到2021 年底我国风电装机容量已突破3亿千瓦。但风电渗透率的不断提高给电力系统的正常稳定运行带来了巨大挑战,首先是因为风能具有波动性和随机性,风电的大规模接入会增大电网系统净负荷波动的幅值和速率;其次风电机组往往采用最大功率跟踪模式运行,并通过电力电子装置接入电网,导致电网惯性降低,并且转子动能被隐藏,转子转速与电网频率处于解耦状态,使得风电机组无法实现惯性响应和一次频率调节[2]。
为了提高风电机组对电力系统频率变化的响应能力,维持系统频率稳定,使风电机组具备一次调频能力,目前常采用不同的控制策略来利用风电机组本身隐含的转子动能的能量[3],但受转子转速约束和变桨控制响应慢的影响,控制过程比较复杂,难以满足系统调频需求,并且会损失一部分经济效益。因此,通过具有快速负荷响应的储能系统耦合风电机组进行频率调节成为研究热点[4]。近年来国内外利用电化学储能辅助风电进行调频的工程项目发展迅速,虽然取得一定的效果,但是电化学储能存在燃烧和爆炸风险、对温度敏感和废弃物回收等问题[5-6]。飞轮储能作为一种新型物理储能技术,具有功率密度大、响应速度快、长寿命、环境影响小、可扩展性好、无污染等特点,可以很好地匹配频率调节频繁的功率波动以及有较小时间尺度的要求,因此比较适合辅助调频以及新能源消纳等应用场景[7-8]。
目前飞轮储能系统的应用研究集中于辅助火电机组调频以及平滑风电功率波动等,文献[9-11]发现利用飞轮储能系统辅助火电机组进行一次调频和二次调频,可以明显提高机组的调频性能,减少火电机组的调频负担。文献[12]通过在风光储基地搭建飞轮储能系统进行实际充放电验证,表明飞轮储能系统运行稳定、可靠,其功率、容量和响应速度等均具有显著优势。文献[13-14]采用飞轮储能系统平滑风电的输出功率,显著降低了风电功率的波动量。文献[15]通过利用飞轮储能协同风电机组运行,不仅有助于提高系统恢复同步稳定的动态特性,而且能够降低同步发电机参与调频的有功调节速度要求。《并网电源一次调频技术规定及试验导则》规定风电场必须具备一次调频功能,一次调频主要针对变动幅度小、周期很短的负荷波动,考虑将小负荷波动下调频任务由飞轮储能单独承担,利用飞轮储能装置的快速响应能力协助风电机组进行一次调频控制,不仅提高系统频率的稳定性,而且简化风电机组的协调控制,提升风电消纳,具有较好的应用前景。
本工作在传统电力系统频率分析模型的基础上,研究飞轮储能参与一次调频对电网频率特性的改善效果,采用传递函数进行等效建模,建立飞轮储能辅助风电进行一次调频系统低阶线性模型,通过传递函数分析系统的频率特性,在阶跃负荷扰动和连续负荷扰动的条件进行飞轮储能辅助风电一次调频的仿真验证。
1 电力系统一次调频原理
电力系统一次调频是指当电力系统频率偏离目标频率时,电源通过控制系统的自动反应,调整有功出力减少频率偏差的控制过程,一次调频属于有差调节。基于同步发电机的传统电力系统的一次频率模型是一个闭环控制系统,主要包括调速器、汽轮机及发电机与负荷等。在分析电力系统总体频率特性时,忽略对电压和功角的动态特性研究,采用小信号模型将电力系统频率一次调频模型简化为图1所示[16]。

图1 同步发电机组一次调频模型Fig. 1 Primary frequency modulation model of power system of synchronous generators
图1 中,R为调差系数,T为汽轮机的等值惯性时间常数,a为汽轮机的特征系数,M为与系统惯量相关的转子时间常数,D为负荷的有功频率响应系数,ΔPm为汽轮机变化功率,ΔPL为负荷变化功率,ΔPe为负荷变化总功率,fref为参考频率,f为实际频率,Δf为频率变化量。
2 飞轮储能辅助风电一次调频分析
2.1 飞轮储能辅助风电一次调频模型
假设某区域电网发电单元场景主要由风电场和火电机组构成,飞轮储能作为辅助风电的调频系统,飞轮储能单元主要组成结构包括飞轮本体、双向电机、机侧变流器,通常由多个飞轮储能单元通过直流母线并联到网侧变流器组成飞轮阵列系统,同时为了简化控制,飞轮储能系统采用集中配置的方式布置在风电场出口母线处,并通过升压变等设备并入电网,系统拓扑结构简图如图2所示。
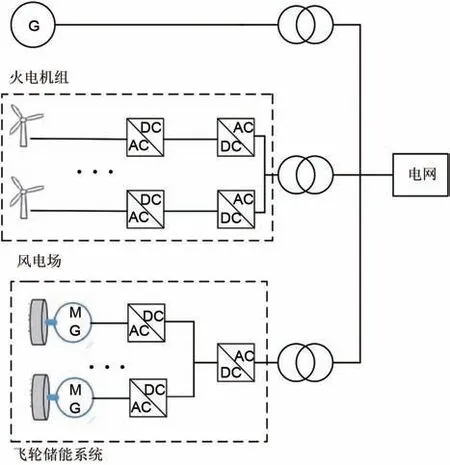
图2 区域电网简化结构图Fig. 2 Simplified structure diagram of regional power grid
根据图1,忽略火电机组具体的调速器控制、汽轮机模型、限幅等非线性环节与二次调频,典型火力发电系统中调速器和汽轮机部分的传递函数为:

风电机组是一个非线性系统可通过转子惯性控制、超速控制和变桨控制等,使其具备一次调频能力。其中变桨距控制调节能力较强,调节范围较广,适用于所有风速模式[17]。当风电机组通过利用桨距控制器进行变桨控制,改变桨叶角度调整机组出力以减少电网频率波动时,风电机组处于最大功率点之下的某一运行点,以留出一定的备用容量,因此风电机组的一次调频模型等效为一阶滞后传递函数[18]:
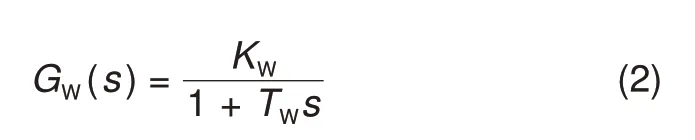
式中,KW为风电机组一次调频系数,TW为风电机组的变桨控制响应时间常数。
飞轮储能的基本原理是绕定轴旋转的飞轮转子通过转速变化实现能量转换,转子加速过程存储能量,减速过程中释放能量。飞轮系统存储的能量与飞轮转子的转动惯量和转速有关,可以用下列公式表示:

式中,E为飞轮转子所具有的动能,J;J为飞轮转子的转动惯量,kg·m2;ω为飞轮转子的工作转速,rad/s。
为着重分析飞轮储能参与一次调频的效果,通常采用一阶惯性模型作为飞轮储能的等效模型,并以虚拟下垂控制作为飞轮储能参与一次调频的控制方法[18-19],则飞轮储能控制系统由飞轮出力控制模块和飞轮传递函数模块组成。飞轮储能控制系统的传递函数可以表示为

式中,KF为飞轮储能系统的下垂控制系数,TF为飞轮储能系统的时间惯性常数,通常取决于飞轮储能系统本身的特性。
随着风力发电比重的提高,逐渐代替火电等常规同步发电机组,电力系统中提供惯性和一次调频响应的调节资源逐步减少,表现为电网等效惯性时间常数减小。定义常规同步发电机组系数K:

K的取值范围为0≤K≤1,则同步发电机组系数为K的系统负荷-频率响应函数为:

为了分析飞轮储能辅助风电调频的系统频率特性,根据图2 的电网结构简图,火电机组模型用式(1)表示,风电机组变桨调频模型用式(2)表示,飞轮储能控制模型用式(4)表示,得到飞轮储能辅助风电一次调频的响应模型,如图3 所示,图中,ΔPF为飞轮储能调频提供的功率,ΔPW为风电机组调频提供的功率。
2.2 飞轮储能辅助风电一次调频频率特性分析
根据图3,当常规火电机组发电系数为K时,风电渗透率为1-K,设定输入的参考频率为0,分别讨论以下三种场景在负荷功率变化时的频率响应特性。
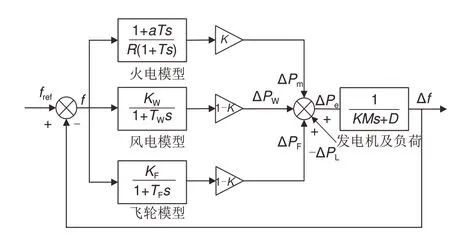
图3 飞轮储能辅助风电一次调频控制模型Fig. 3 Primary frequency modulation control model of flywheel energy storage assisted wind power
场景1:风电机组并入电网,但不考虑风电机组调频能力,只依靠火电机组的调频能力,记作系统S1,系统S1的频率响应函数为:

场景2:风电机组通过留有备用容量参与一次调频,但飞轮储能系统不接入电网,系统的调频资源由火电机组和风电机组提供,记作系统S2,系统S2的频率响应函数为:
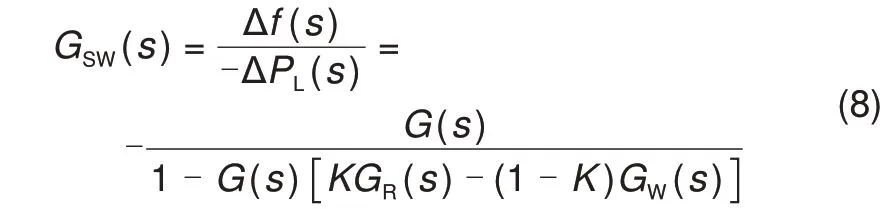
场景3:飞轮储能系统接入风电场的母线处,风电机组并入电网,但不计及风电机组一次调频能力,采用飞轮储能系统辅助风电进行调频,记作系统S3,系统S3的频率响应函数为:

当电力系统在受到负荷扰动ΔPL时,采用终值定理分别计算上述3 种场景的稳态频率偏差Δfss、Δfsw、Δfsf,公式为:
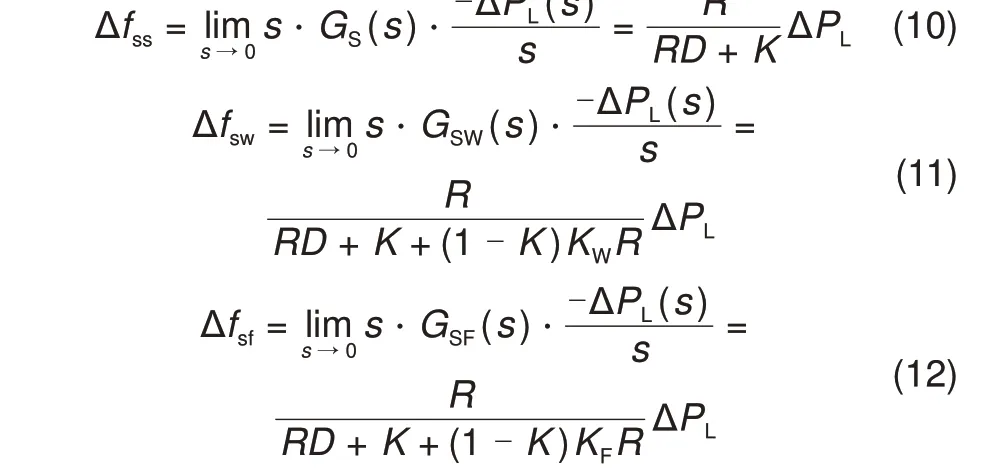
由式(10)、(11)和(12)可以看出:
(1)有风电渗透的电力系统的稳态频率误差主要与同步发电机组系数K有关,这表明,如果风电机组不提供频率控制能力,在一定的负荷扰动下,系统的稳态误差随风电渗透率的增加而增大,系统频率维持工频同步和抗扰动的能力也会随风电渗透率提高而下降。
(2)相比于风电机组不参与调频,通过加入飞轮储能或者风电机组参与一次调频时,都能够降低电力系统频率的稳态误差,从而增强系统频率维持工频同步和抗扰动的能力。
2.3 飞轮储能容量配置
飞轮储能的容量配比是辅助风电参与一次调频的重要问题,为了满足系统在较高风速的一次调频能力,减少弃风量,假设风电场以额定功率PW(MW)发电,需要配置的飞轮储能的功率等于风电场通过变桨控制具备一次调频能力时提供的备用功率,则飞轮储能需要功率ΔPF和容量E如下式:

式中,Δf为一次调频稳态频率变化量,RW为风电一次调频系数,t为一次调频投入时间。
在整个频率响应过程中,衡量系统性能的关键指标包括频率变化率幅值、峰值频率、稳态频率和频率调节时间,以文献[20]的频率稳定运行标准作为衡量系统运行性能指标的标准,如表1所示。
从表1 可知,在一次调频过程中需要满足稳态频率偏差Δf在±0.2 Hz的范围内。当风电一次调频系数RW取0.04,Δf取0.2 Hz,fref取50 Hz,t取20 s,代入式(13)和得到ΔPF=0.1PW(MW),E=0.56PW(kWh),故取飞轮储能的功率为风电场额定功率的10%,容量满足0.56PW(kWh)时,可以满足风电场一次调频的频率指标。

表1 动态性能指标标准Table 1 Standard of performance indices of IR and PFR
3 仿真分析
以上述的飞轮储能辅助风电的频率控制模型为基础,在Matlab/simulink中建立图3所示的飞轮储能系统辅助风电机组一次调频系统的仿真模型。选取各项参数如表2所示[15,18],参数以额定负荷1000 MW及额定频率50 Hz为基准进行标幺化。为了减少动作次数,设置调频动作死区为±0.03 Hz,即频率波动绝对值小于0.03 Hz 时,电网频率处于稳定状态,调频系统不工作,飞轮储能系统的功率出力策略如图4。

表2 仿真参数Table 2 Parameters in simulation
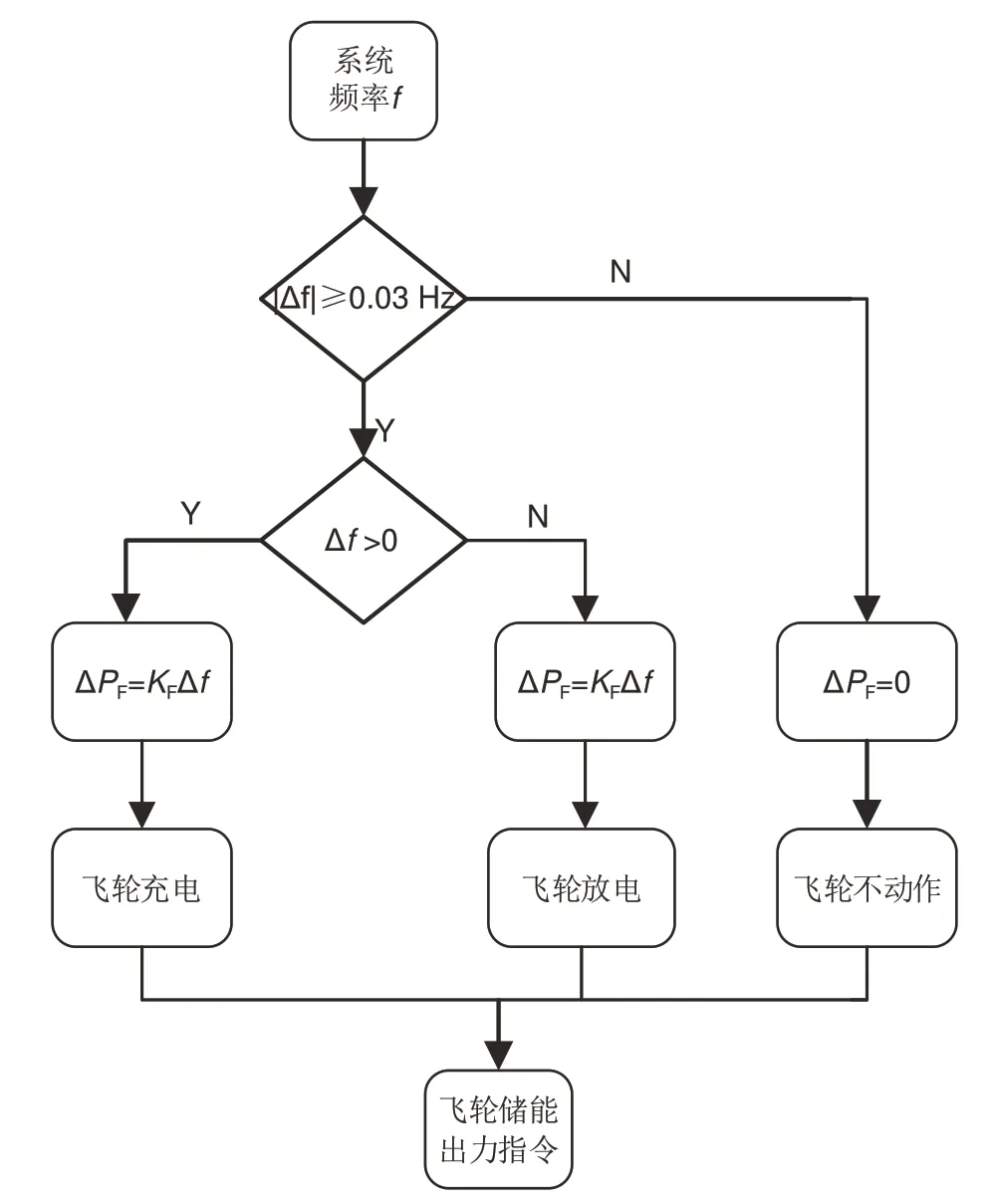
图4 飞轮储能出力控制策略Fig. 4 The output strategy of flywheel energy storage
3.1 风电渗透率对电力系统频率的影响
在场景1的仿真条件下,比较不同风电渗透率的频率响应,设风电渗透率为p(p=1-K),在5 s时加入幅值为0.05 pu 的阶跃负荷扰动,系统的频率变化曲线以及动态性能指标变化如图5 和图6所示。
通常稳态频率作为衡量一次调频的重要性能标准,在不考虑风电机组的调频能力时,从图5和图6 中看出,对于0.05 pu 的负荷功率阶跃,当风电渗透率为30%,即K=0.7时,稳态频率偏差控制在0.2 Hz,符合表1的稳态频率要求。当风电渗透率继续增加,系统惯性持续减小,系统的稳态频率逐渐降低,系统的低谷/高峰时频率偏移增大,频率变化率幅值不断增加,电力系统的频率特性不断恶化,因此风电场必须具备相应的一次调频能力来改善系统的频率响应特性。

图5 阶跃扰动下不同风电渗透率的频率变化Fig. 5 Frequency variation of different wind power penetration under step disturbance
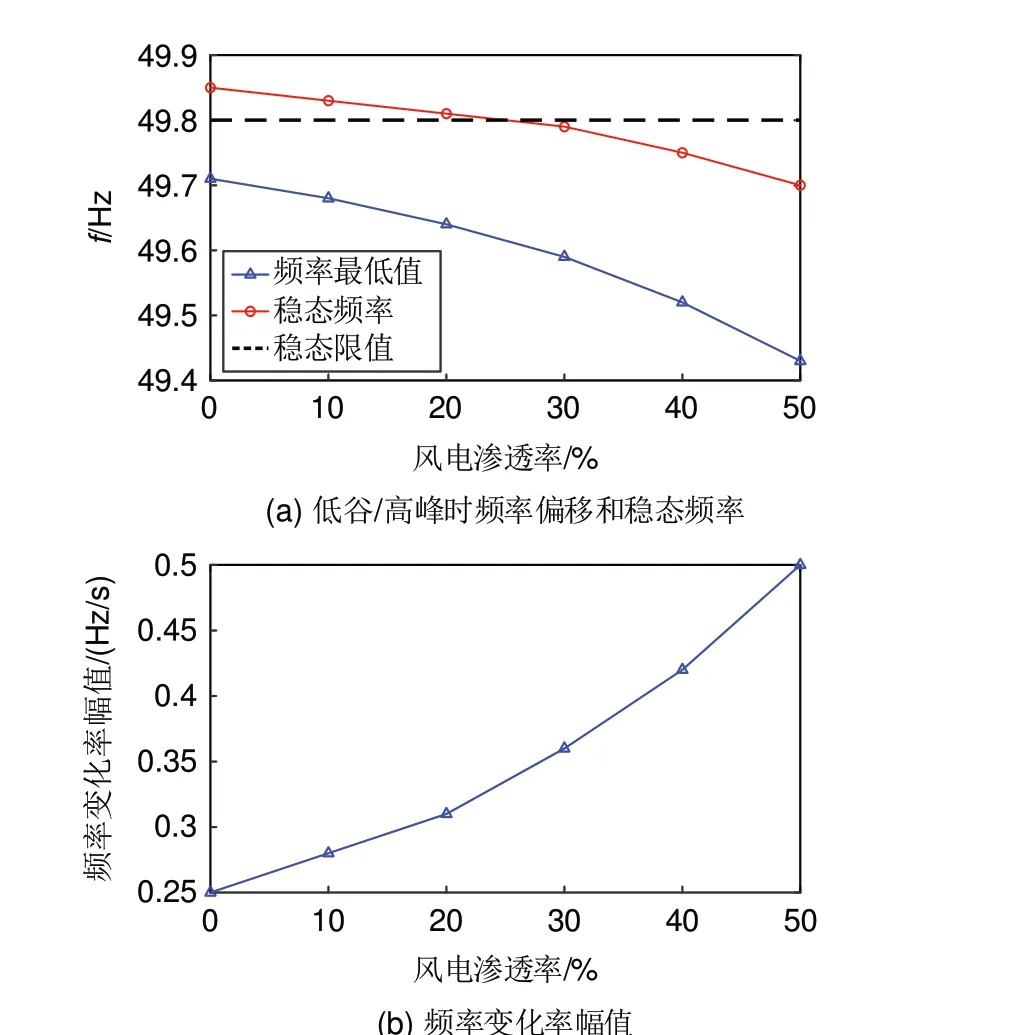
图6 不同风电渗透率的动态性能指标Fig. 6 Performance indices of different wind power penetration under step disturbance
3.2 阶跃扰动下仿真分析
假设风电场运行在额定风速,设置风电渗透率为30%(K=0.7),飞轮储能的功率为风电场额定功率的10%,即风电出力为300 MW,飞轮储能的额定功率为30 MW,需要的调频容量为168 kWh。基于一次调频经验,飞轮储能系统需至少满足30 s~2 min 的能量支撑,目前应用于电力系统的飞轮储能单元为250 kW/50 kWh,可由120台飞轮储能单元组成阵列,即可满足一次调频能量需求。在5 s时加入0.05 pu 的阶跃负荷扰动,分别对系统S1、S2和S3的三种场景进行分析,三种场景的频率变化、一次调频功率变化以及频率性能指标分别如图7和表3所示。
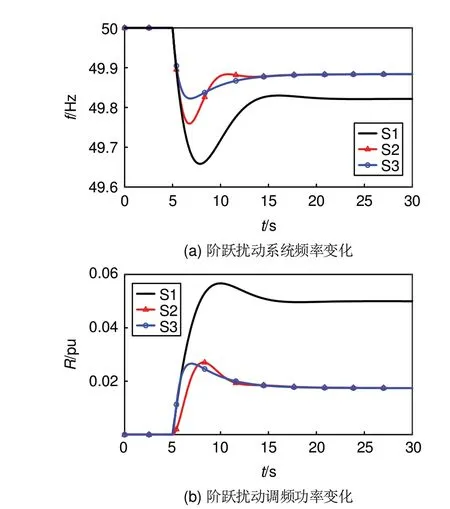
图7 阶跃扰动下系统频率和功率变化Fig. 7 Frequency and power variation of system under step disturbance
从图7和表3可以看出,当系统负荷功率发生阶跃扰动时,在系统S1风电机组不参与一次调频时,电力系统的调频功率完全由火电机组输出,电力系统的频率跌落较大,频率的最低值为49.66 Hz,稳态频率为49.82 Hz;在系统S2 风电机组参与一次调频时,风电机组通过释放备用功率来进行频率调节,频率的最低值为49.76 Hz,稳态频率为49.88 Hz;在系统S3 飞轮储能单独辅助风电场参与一次调频时,飞轮储能输出功率和风电一次调频释放功率基本相等,相对于系统S1 的单独依靠火电机组一次调频的功率有明显降低,并且由于飞轮储能响应速度更快,单位时间输出能量大,飞轮储能调频的频率最低值为49.83 Hz,频率变化率相较于系统S1和S2有所降低,各项指标均符合表1的动态性能要求。
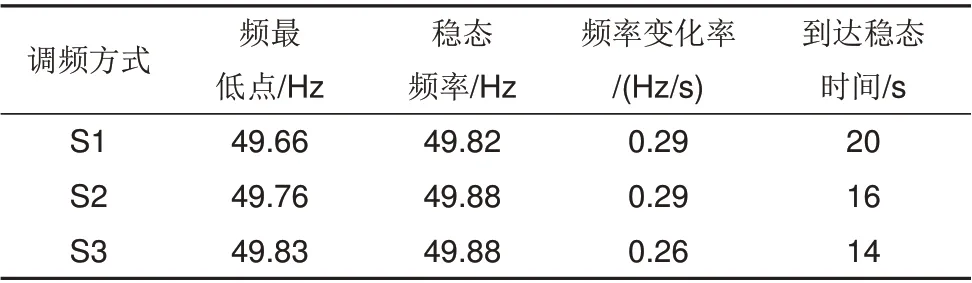
表3 不同调频方式下动态性能指标Table 3 Performance indexes under different frequency modulation modesandard
3.3 连续扰动下仿真分析
负荷功率发生阶跃扰动时,飞轮储能的加入可以提升风电机组的一次调频效果,但负荷功率的波动通常是无规则的连续波动,因此需要分析在负荷功率连续扰动时一次调频的效果。
为了模拟系统负荷的连续扰动情况,采用信号叠加的方法生成随机扰动信号,信号扰动幅值范围为[-0.035,0.045] pu,单向最大幅值为0.01 pu,如图8 所示,其余仿真条件与3.2 节相同,分析系统S1、S2和S3的频率变化和调频功率变化,仿真结果如图9所示。
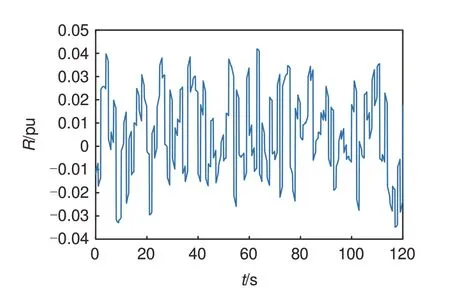
图8 连续负荷扰动曲线Fig. 8 Continuous load disturbance curve
根据图9 的结果,如果负荷发生连续扰动时,在系统S1 时,系统频率的最小值为49.76 Hz,最大值为50.25 Hz,系统的标准方差为0.09592 Hz;在系统S2 时,系统频率的最小值为49.82 Hz,最大值为50.17 Hz,系统的标准方差为0.0751 Hz;在系统S3 时,系统频率的最小值为49.88 Hz,最大值为50.12 Hz,系统的标准方差为0.04904 Hz,满足系统的频率偏差在±0.2 Hz 之间,说明在负荷发生连续扰动时,飞轮储能装置能迅速跟随系统负荷的功率变化,降低系统的频率偏差,比风电机组参与调频的性能效果更好。

图9 连续扰动下系统频率和功率变化Fig. 9 Frequency and power variation of system under continuous disturbance
4 结 论
本工作讨论在风电大规模并网的场景下,探讨对风电场增设飞轮储能系统对电网频率的影响,在Matlab/simulink中建立飞轮储能辅助风电一次调频的线性模型,通过模拟仿真得出如下结论。
(1)在风电本身不参与电力系统调频,随着风电渗透率的不断提高以及同步发电机组占比的逐渐减少,系统频率的下降情况会越来越严重,通过采用飞轮储能系统可以有效提高电网频率的抗干扰能力,抑制频率跌落作用显著。
(2)通过对区域电网耦合10%风电额定功率的飞轮储能系统参与一次调频时,在系统负荷功率发生阶跃扰动时,频率的最低点偏差和稳态频率偏差相比于无调频时分别提高了50%和33%,相比于风电调频时频率最低点偏差提高了29%;在系统负荷功率发生连续扰动时,飞轮储能参与一次调频的频率偏差始终稳定在±0.2 Hz,频率偏差的峰谷差比无调频和风电调频分别降低了51%和31%,频率标准方差分别降低了48%和35%,加入飞轮储能系统的一次调频响应效果明显优于风电通过变桨距控制的一次调频响应效果,有效遏制了由于风电并网导致的系统频率特性的下降。
