液力变矩器叶轮能容定向优化反设计方法
2023-02-27柯志芳魏巍刘城郭猛张嘉华闫清东
柯志芳,魏巍,刘城,郭猛,张嘉华,闫清东,3
(1.北京理工大学 机械与车辆学院,北京 100081;2.北京理工大学 济南前沿技术研究院,山东 济南 250300;3.北京理工大学 车辆传动重点实验室,北京 100081;4.北京理工大学 重庆创新中心,重庆 401122)
0 引言
液力变矩器作为一种液力传动系统的核心部件[1-2],广泛应用于坦克装甲车辆、工程机械、轮船以及民用车辆中,其变矩性能、效率性能和能容性能的提升,或指定性能以及多项性能的同步提升,是变矩器的核心设计目标之一。
以“叶形-流场-性能”为设计思路的变矩器[3],采用类似压气机、轴流泵和离心泵等旋转机械的叶轮叶片以及机翼、螺旋桨叶等翼型的正向设计方法,虽然能快速建立较复杂的变矩器叶栅系统,但相对来说其设计成本高、效率低,过度依赖专业和经验,优化过程具有较大盲目性等,且设计过程间的反馈较弱,设计-流场-性能之间存在着相对割裂的现象。由于流场能决定性能,而叶形能塑造流场,如果从流场的角度设计叶片,可视为基于流场直接设计性能,且流场设计结果可以反馈到设计中,这正是反设计方法(IDM) 的设计思路。
IDM 作为一种不同于正向设计方法,是一种带有反馈设计且具有良好前景的设计方法,其基本思路是预先利用能代表特定性能的流场特征分布[4]来确定叶片叶型结构。这一理论已经在压气机[5-6]、轴流泵轮机械[7-9]和涡轮机械[10-14]等领域应用,其中一种典型流场特征为一系列涡旋矢量,其强度由约束环量2πθrvθ的特定分布形式确定,其中,vθ为平均周向速度,其大小与叶片偏转角度相关,r和θ 分别为径向距离和周向角度参数,因此叶片形态不需要求解复杂流场即可反求得到。
目前叶片IDM 主要有3 种: 复特征线法[15]、虚拟气体法[16]和势流函数法[17]。叶片IDM 通过设计叶表载荷来设计叶片,而非直接设计叶片几何参数,这样可以实现基于流场特性的定向设计,从而提高设计速度,减少盲目性[18]。
在汽轮机以及涡轮机械等领域有诸多学者通过分析和对比不同正向设计得到的叶片结果[19],得到不同特性的叶表载荷特征,从而提高载荷设计成型率。同时在设计与优化方面,通过叶片IDM 与优化算法相结合的方式[20-22],在给定载荷基础上,以指定性能结果为目标进行定向优化设计,能够得到符合实际需求的设计解[23-24],证明了这种方法的可行性。
IDM 的主要优点是,基于约束载荷的简单分布,可以快速设计具有可控三维压力场叶片的复杂三维叶片形状[25-26]。这种方法可应用于泵轮、涡轮、扩散器等叶片的设计中。扩散器与变矩器叶轮叶片的设计过程基本相同[27-29],不同之处在于应考虑来自上游叶轮不均匀来流的影响。为了扩展该方法,还可以设置包括入出口剪切流的影响,这对于变矩器这类深受非均匀入出口流场影响的叶片反设计十分重要。
本文提出液力变矩器叶栅IDM,并在基本保证变矩器性能的基础上对泵轮能容进行定向提升的反设计。
1 反设计方法
1.1 反设计理论
已有反设计理论[30]中,假设流体是无黏的,叶片无限薄,尾流引发的冲击效果导致的熵变场会被忽略;同时经典空气动力学方法是利用边界涡量来表征叶片形状的,这一方法在具有循环流动特征的液力变矩器中仍可采用,但不同的是需要考虑流体的黏性特性和不可压缩特性,此时熵变将用压力梯度替代。基于反设计理论[4,11],假设来流是稳定无旋流场,则边界的涡量结果为
式中:δP(α)为周期Delta方Δ程[31],α为周向角度;r 为离线位置的离轴半径;为哈密顿算子;vt为叶表周向速度分量;为周向速度均值;α 为叶片偏转角。由α 表征的叶片表面如下定义:
式中:(z,r,θ) 为右手坐标系下液力变矩器流道的空间坐标点;γ 为叶片沿着流线方向的偏转角;i 为不大于叶片数的非负整数;NB为叶片数。
对于强迫涡流流动的叶片结果,上述两方程分别代表的是叶片尾流的涡量和叶表吸力面附近的尾流,并且轴流面上的速度是指周向流场速度的节角均值结果,即
式中:标量ϕ=ϕ(z,r,θ) 为速度矢量的势能部分,其余项则是表示的旋转部分;S(α) 为周期性锯齿函数[31],代表周期性速度结果。由此可知式(1) 即式(4) 所示速度场的散度结果。
针对可压缩流体反设计,Zangeneh[10]利用预给定值来表征周期性节角均值速度,因而容易将速度矢量场分解为上述包括二维轴截面上节角周期均值速度和剩下三维中与轴截面垂直的周向旋转速度两部分,不过因为叶表的周向速度均值为零,因此并未纳入实际计算叶片偏转角的部分,而是单独用于计算运动方程中的周期分量,这一点同样适用于不可压缩流体。
1.2 变矩器中的反设计
对于变矩器这类多叶轮旋转机械,其来流流场时并未充分发展且存在较大周向速度分量的周期性结果,因此需要将其他部分进一步利用来计算偏转角。根据Dang[11]提供的思路,运动方程以守恒的形式进行计算,如此利用周向分量同样可以计算,尾流的冲击部Δ分,因此可以直接将速度矢量定义为
式(6) 不仅包含平均速度的散度结果,同时又等价于周向流场的均值涡量,因此更有实践意义。同时需要一个新型叶片参数表征方法,而非单纯的叶片形状控制点或者流场压力载荷分布参数。
对于变矩器流场载荷构造,首先需要明确的是,变矩器的三维或准三维内流场结果中,其周向环面、流向流面以及展向节面流场均为非定常瞬态流场。其中内流场各个截面,曲线位置及其对应方向如图1 所示。图1 中:ω 为旋转速度,lsp、lci、lst分别为展向、周向和流向方向的归一化位置。
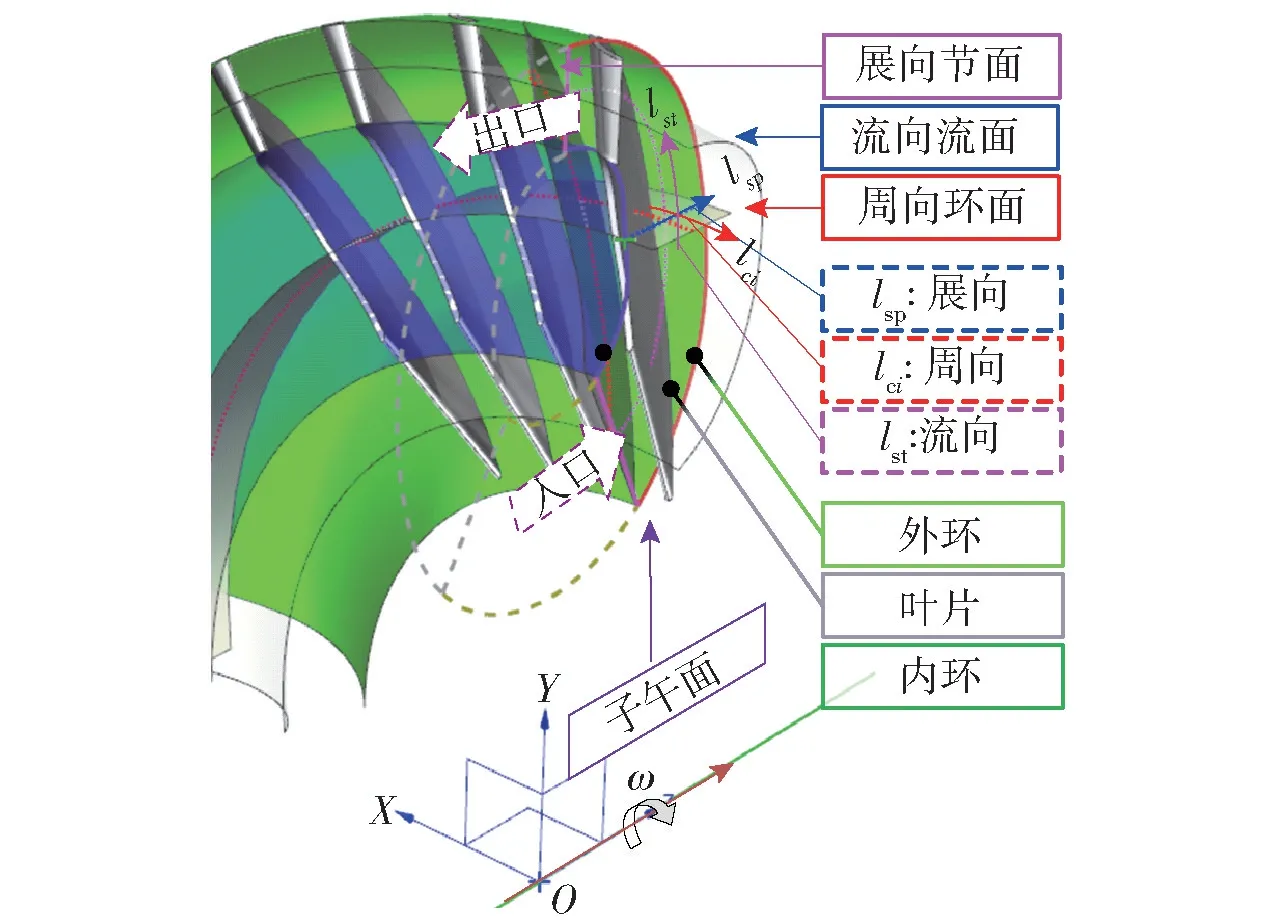
图1 流道截面曲线及其方向示意图Fig.1 Diagram of flow passage section curve and direction
出于设计需求,假设叶片无限薄,同时设计流线(即节面流线) 上的流场结果由该叶表流场的质量平均周向速度矢量表征,即
式中:PS 表示叶表的压力面;SS 对应叶表吸力面;ρ为流体介质的密度;V 为体积。针对变矩器内部流场,其内部传动介质为不可压缩流体,因此等温流动假设时密度不变,同时由于存在周期性特征,可将载荷rvt简化为周向的单周期流场载荷结果:
式中:N 为流道叶片数;γN为节角,因此γN=2π/N。设计点叶表两侧的流场在轴截面周向上受力结果仅为流体压力,然而实际上难以直接找到质量平均周向速度矢量值与叶表压力差以及相应的压力之间的数值关系。为此,有学者[10-11,32]提出一种可以根据量纲分析以及满足流体压力的压差计算方法,首先Crocco 形式的动量方程为
式中:FB为叶表压差造成的垂直于叶表表面的压差力。
式(9) 右侧部分即表示流体在叶片表面形成的反作用力。由于叶片表面的流体速度应与该表面的偏转角垂直,有
式中:vB为叶片吸力面表面周向流场的平均速度。
将式(10) 和式(1) 代入式(9),可以得到叶片所受的流体压差力结果:
式中:rvst,LE和rvst,TE分别为叶片前缘和叶片尾缘的叶表载荷矢量。值得注意的是,此处的叶表速度vB在叶表附近可产生非零结果,而在叶片尾流无叶片区域中,由于叶片所受流体作用力不存在,有vB·(rvst,LE-rvst,TE)=0 N,因而通过对叶表载荷矢量rvst分布的合理设计,即可对尾流无叶片区域结果进行表征和设计。
对于一个无限薄的叶片,同时叶片在不可压缩且无旋流场中,其压力差Δp 可由上述参数的导数表示:
式中:p+、p-分别为叶表压力面和吸力面的压力;lst为归一化的流线位置。因此可以将∂(rvt)/∂lst分布作为输入条件限制其峰值结果,即可优化压力载荷分布,进而优化流场结果。
2 高能容变矩器叶表载荷特性
对于变矩器,提高泵轮叶片的转矩特性,即可提升变矩器的能容特性,因此可以利用流场载荷特性定向优化能容特性。首先选取能容依次增大,弯曲程度也以此增加的P1、P2和P3等3 种泵轮叶片设计案例,对高能容变矩器叶表载荷特性进行探究。
研究结果表明,当入口流场方向基本等于泵轮叶片入口角度时,泵轮可达到最高效率,同时该工况下涡轮与泵轮转速之比(即速比SR) 也更接近位于起动工况和高效工况之间的变矩器常用工况,因此可以通过对入口角度的控制,将常用工况的速比设计为高效工况的速比,此时叶片环线的叶表载荷分布结果如图2 所示。
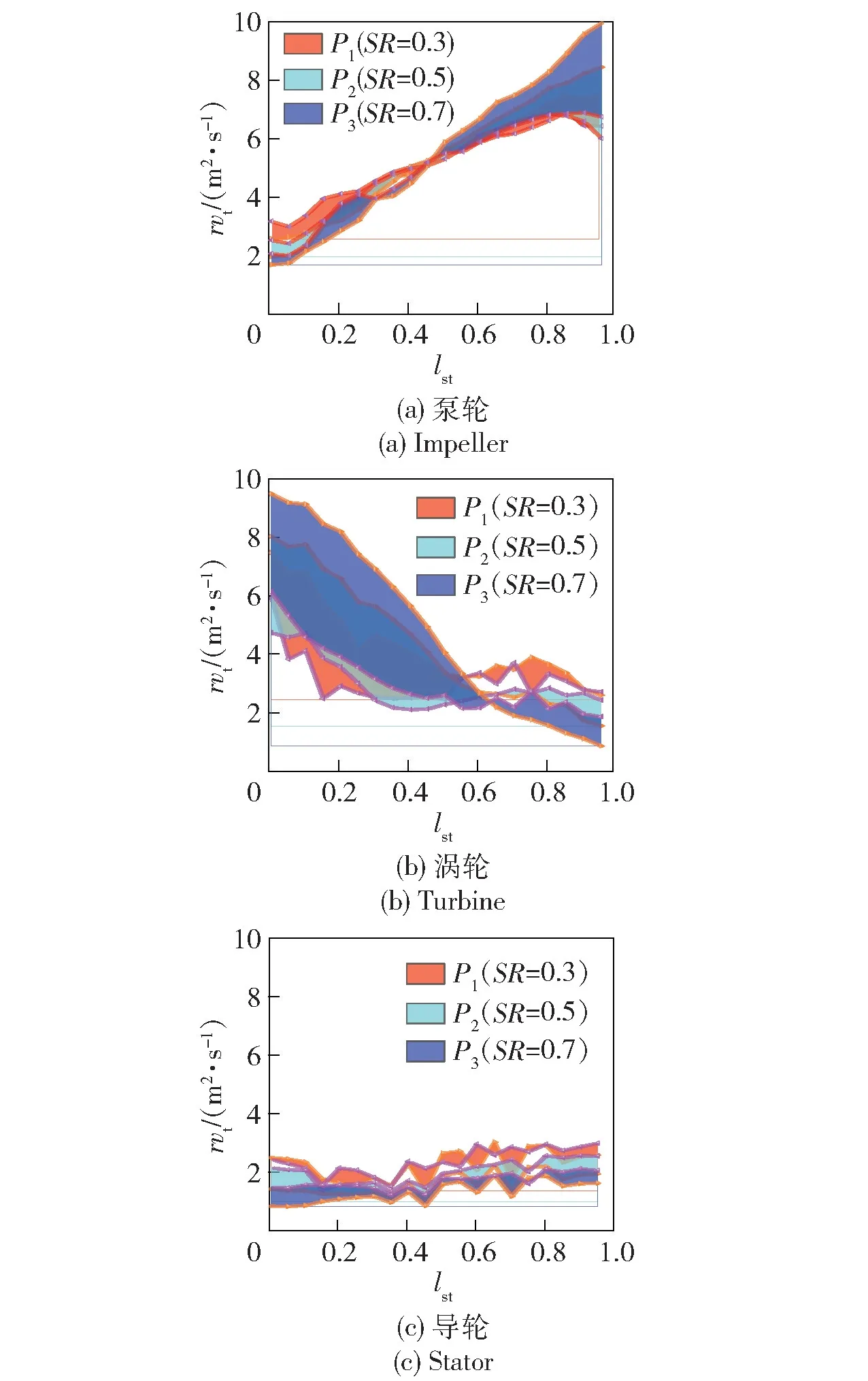
图2 变矩器叶片内外环环线的叶表载荷分布对比结果Fig.2 Comparison result of blade load distribution fortorque converter
由图2 可以看出: 高变矩比的P1案例中泵轮入口位置的载荷较高,出口位置相对上升不多,而涡轮载荷下降并不多,造成涡轮载荷与泵轮载荷之比较高,即变矩比较大;高效率P3案例中泵轮入口载荷较低,流体在泵轮流道中获得能量较高,其出口载荷上升偏高,然而叶片过于扭曲导致叶片出口位置处的载荷分布差异较大,涡轮吸收更多能量并转换为转矩输出,因而能量损失较小,整体效率较高。
进一步对比变矩器泵轮叶表载荷及其入出口叶表载荷差异,将泵轮叶片前缘(LE) 载荷分布rvTE(lsp) 和尾缘(TE) 载荷分布rvTE(lsp) 的差值作为调节泵轮转矩性能的指标,定义为泵轮的动力载荷drvt:
进一步统计各个速比下不同流线位置处的动力载荷如图3(a) 所示,以及动力载荷在相同流线位置的均值结果如图3(b) 所示。
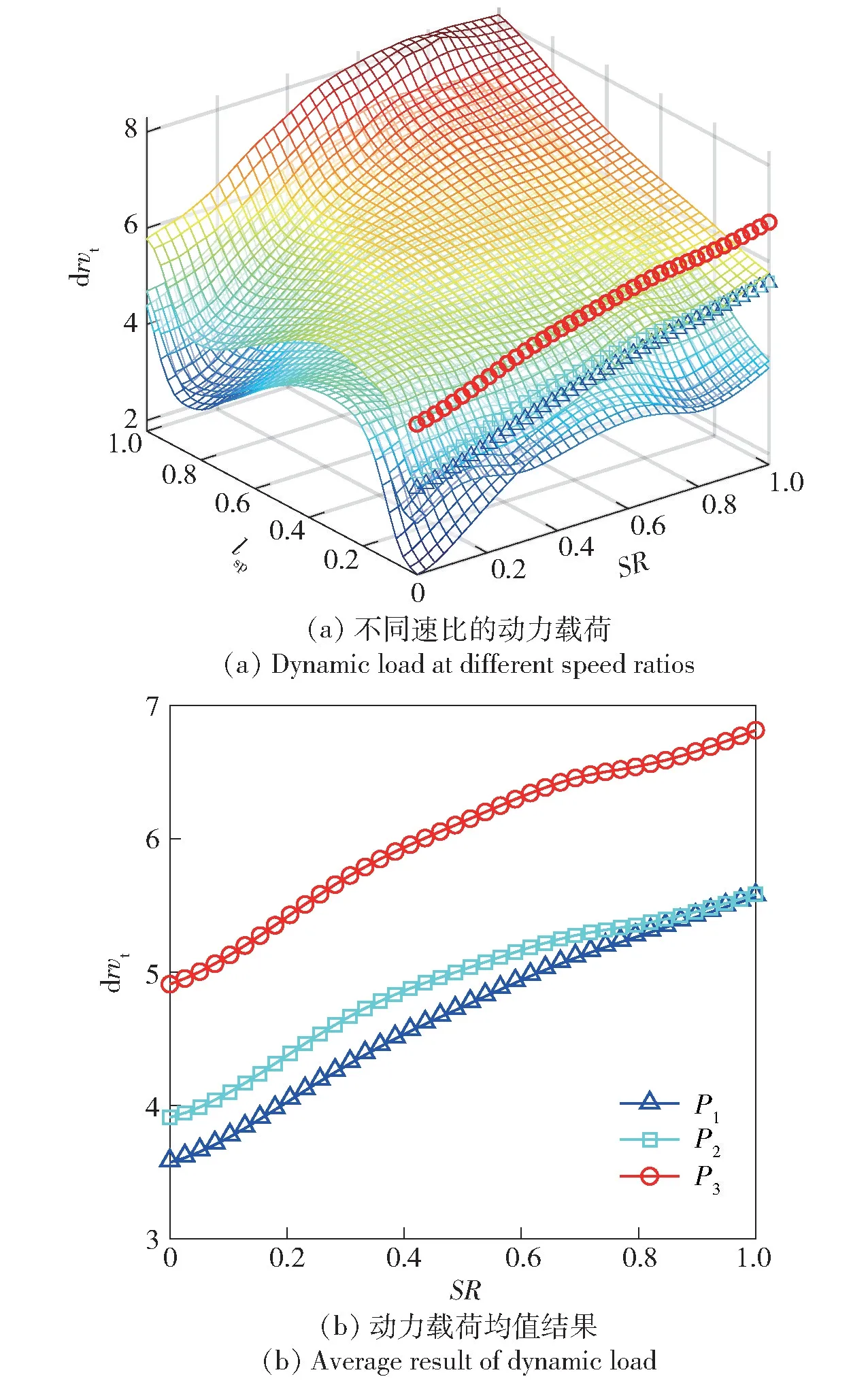
图3 泵轮叶片的动力载荷分布结果Fig.3 Dynamic load distribution result of the impeller blade
图3 中P1、P2和P3叶表动力载荷的均值分别为4.664 6 m2/s、4.897 1 m2/s 和6.012 4 m2/s,可以看到P2的动力载荷相对P1增大了5.0%,对应能容提升了7.05%,P3相对P1增大了28.9%,能容提升了38.13%,结果表明动力载荷差异随着叶形骨线的弯曲而逐渐增大,此时能容结果同样也在逐渐增大,说明入出口叶表载荷差异与能容结果存在强相关关系。
由此可以通过调节动力载荷,对泵轮能容性能进行调节,且动力载荷越大,泵轮能容性能越好。由于泵轮作为动力叶轮,作用是将外界能量转化为传动介质的动能,使得其速度从入口到出口逐渐增加,因此上述动力载荷可表征泵轮对油液做功的能力,若动力载荷越大,则泵轮的做功能力越大,因此叶片转矩与动力载荷之间存在正相关关系。根据上述原理,可以建立基于动力载荷特征的高能容变矩器设计理论,核心在于基于能容指标的变矩器入出口叶表载荷分布构造的方法。
3 泵轮反设计案例
基于第1 节IDM 和第2 节定向能容优化反设计思路,结合内流场的特性,对泵轮叶形骨线进行三维反设计,优化目标是提高泵轮能容性能的同时保证流场平顺性,抑制空化等现象。
3.1 变矩器泵轮反设计
以循环圆直径D=310 mm 的冲压型变矩器为例,进行泵轮叶形骨线反设计。泵轮将设计工况下入口流场与泵轮叶片入射角保持一致,并将此时速比设计为高效工况速比,此时泵轮转速在2 000 r/m,入口流场的流量为0.176 m3/s。提取该设计工况(SR=0.8) 下的载荷分布结果,具体如图4所示。
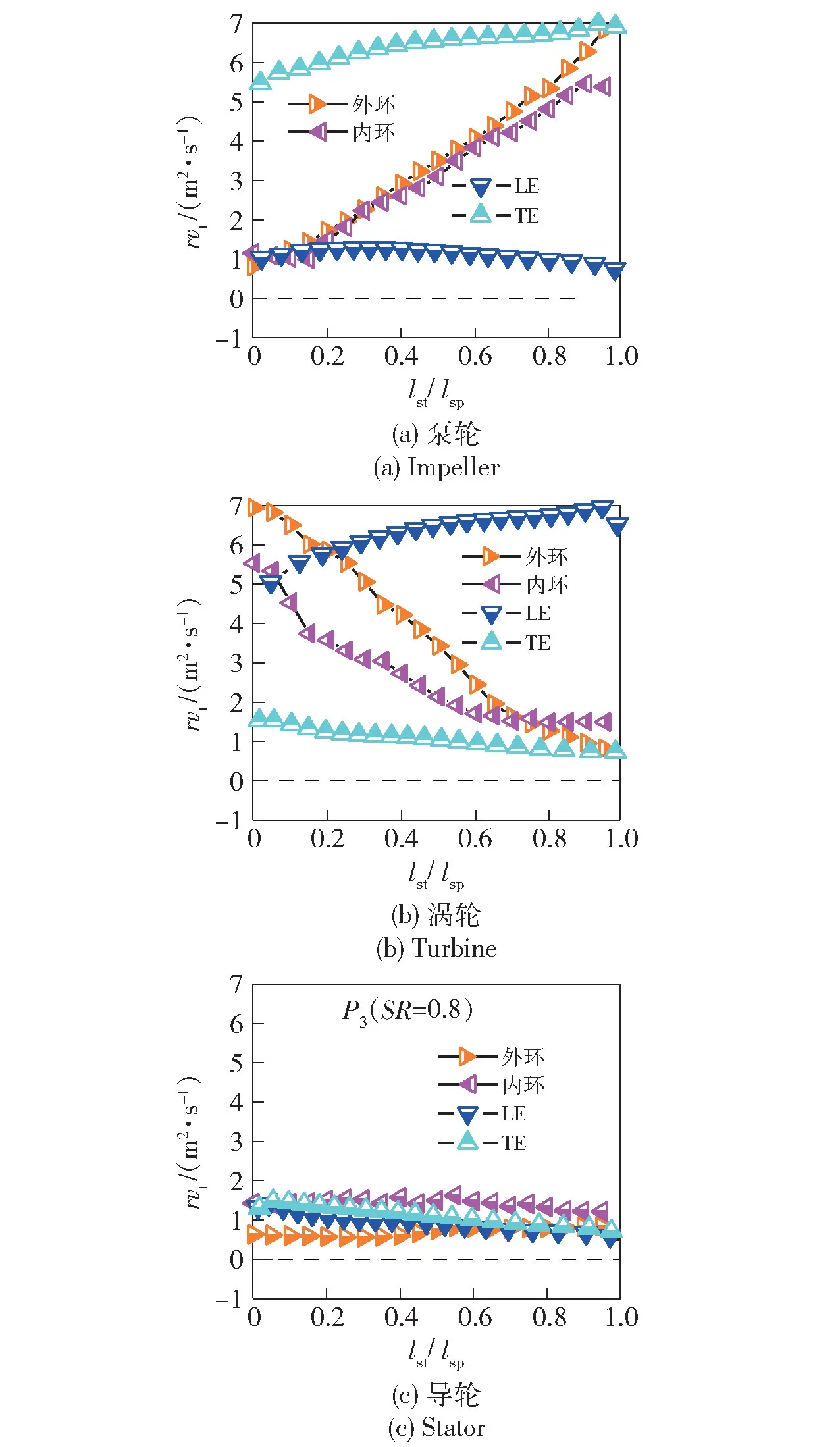
图4 变矩器叶表载荷分布结果Fig.4 Blade load distribution result of torque converter
首先设计泵轮循环圆结果,并给定变矩器入口条件。为减小入口流场对设计结果带来的过大误差,将导轮的部分循环圆作为泵轮循环圆的入口混流区,同时涡轮的部分循环圆作为泵轮出口混流区。由于该位置位于重点设计的LE 与TE 附近,附近网格进行加密,进一步提高了输入条件与变矩器叶片设计的耦合关系。设计区域与网格结果如图5所示。
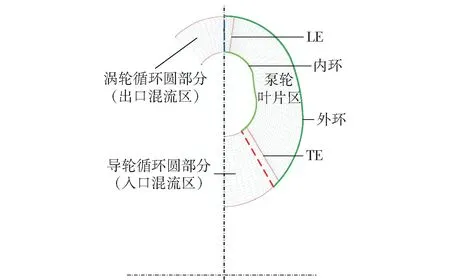
图5 泵轮反设计案例循环圆及其网格结果Fig.5 Torus result of the impeller and the meshing results in the inverse design case
叶片入出口的叶表载荷分布可采取线性拟合。根据第2 节定向能容提升的反设计原理,此处采取的优化策略为: 保持入口载荷不变,提高10%的出口外环处的叶表载荷,优化前后的叶表载荷分布拟合结果如图6 所示。
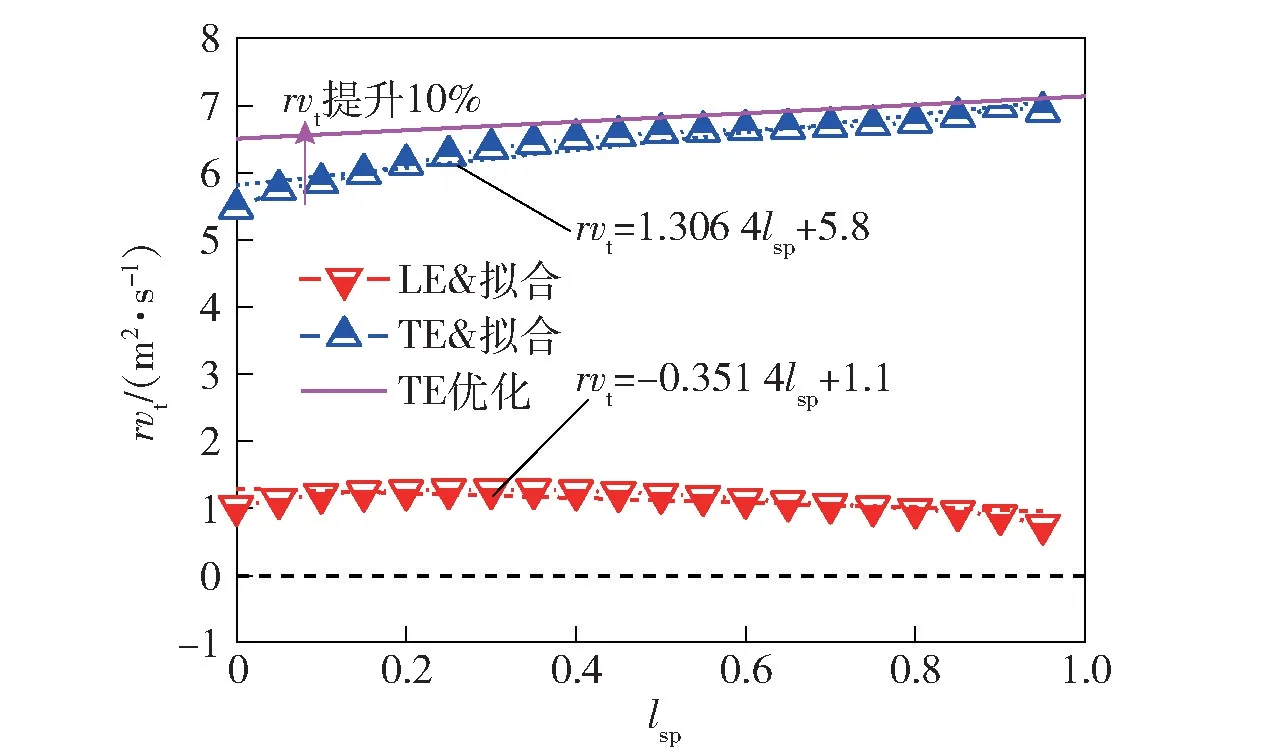
图6 泵轮入出口叶表载荷分布及其优化设计结果Fig.6 Blade load distribution of the impeller and its optimizaiton design result
同时对环线上的载荷分布进行优化的策略为:环线的边界载荷与入出口载荷的边界保持一致,同时优化内外环线叶表载荷梯度,该叶表载荷梯度在入出口位置采用二次函数拟合,中间则用一次函数光滑连接,并保证该载荷梯度的积分结果为入出口的叶表载荷之差(见图7(a)) :
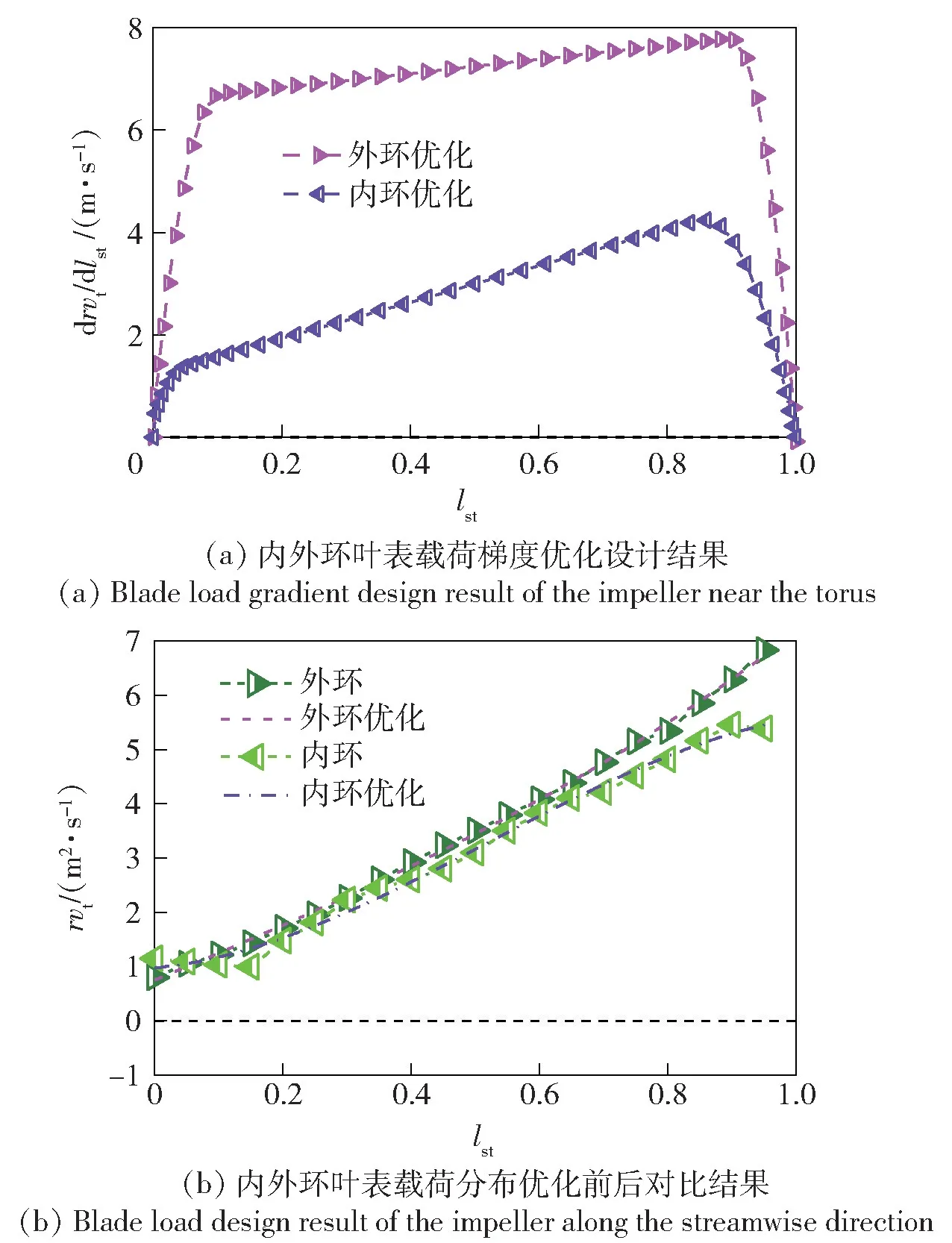
图7 泵轮环线叶表载荷分布的设计与优化Fig.7 Design result of the blade load distribution in the torus
由此设计得到的内外环叶表载荷结果如图7(b) 所示。根据特征载荷结果,可以二维插值求取叶片表面的载荷分布,进一步确定叶表压力差以及叶表偏转角度分布结果,从而确定叶片形状,其中叶表载荷分布结果如图8 所示。图8 中,Z 为轴向距离。
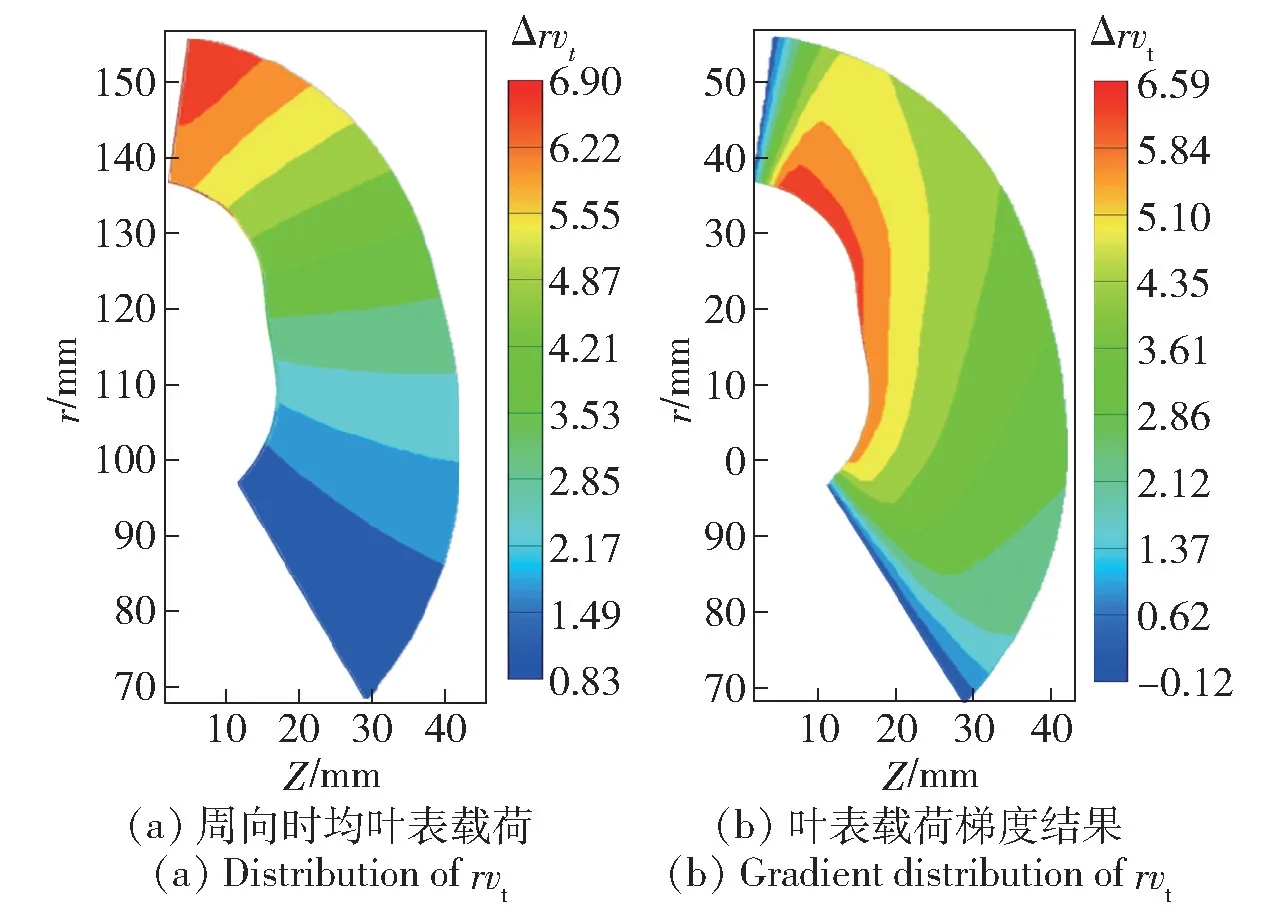
图8 泵轮叶表载荷分布结果Fig.8 Blade load distribution design result of the impeller
进一步对叶片形状进行迭代设计,以满足此叶表载荷要求,并利用三维流动设计平台生成三维叶栅结构。最终的泵轮叶片设计结果如图9 所示。
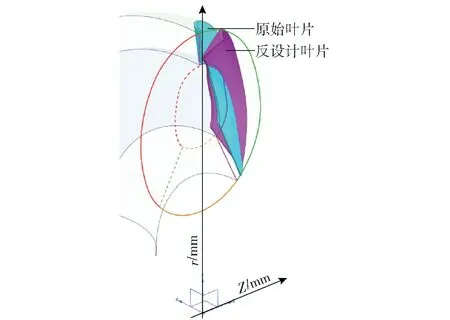
图9 反设计前后叶片对比结果Fig.9 Blade comparison results before and after inverse design
3.2 反设计结果分析与验证
经过3.1 节设计的泵轮叶片,进一步通过变矩器的三维流场仿真模型进行计算流体力学(CFD) 数值计算和验证。对比原始变矩器与反设计泵轮的变矩器,可以进一步发现和探究反设计叶片对性能和流场的影响。
首先二者在性能上的结果差异如图10 所示。图10 中,K、η 和Tp分别为变矩器性能参数变矩比、效率及泵轮转矩,ΔK、Δη 和Δλ 分别为与对应实验结果的相对误差;下标IDM 和ORI 分别表示反设计叶片和原叶片;下标CFD 和EXP 分别表示通过CFD 计算和实验测试得到的性能结果。由图10 可以看出,正如反设计理论所预测,反设计优化得到的样机相比原样机的能容性能有所提升,可以看到能容在SR <0.6 时均有所提升,相较实验结果最大提升17.1%,平均提升达到了13.1%,仅对比CFD 结果,表明可带来5.2%的提升;同时起动变矩比和最高效率特性也分别提升了2.1%和7.5%。由此可见,针对能容的定向设计,使得能容特性得到了大幅提升,因此可以证明IDM 对能容定向设计的有效性。
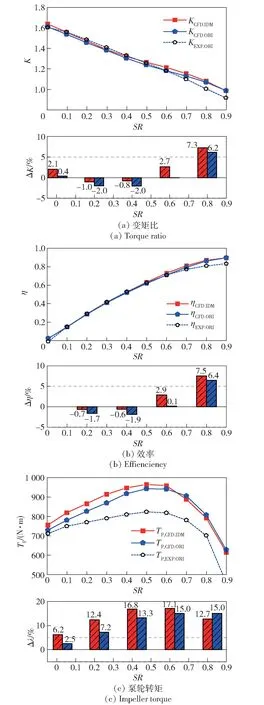
图10 原始变矩器与反设计变矩器性能对比Fig.10 Performance comparison result of the torque converter
此外,反设计对内流场的局部细节同样进行了优化。首先对比反设计泵轮的变矩器轴截面的平均载荷分布,其结果如图11 所示。从图11 中可以发现在设计工况(SR=0.8) 下,IDM 泵轮的最高叶表载荷从6.972 m2/s 下降至6.634 m2/s,同时最低载荷从0.424 9 m2/s 降至0.392 2 m2/s,使得叶表载荷的幅值从6.547 1 m2/s 下降至6.241 8 m2/s,降幅为4.9%,改善了压力梯度的分布结果,从而提高了内部流场的平顺性。同时起动工况的载荷结果也有所改善,其叶表载荷幅值最高下降1.4%,表明本文提出的IDM 可以同时改善变矩器的整体内部流场的平顺性。

图11 平均叶表载荷分布差异对比Fig.11 Comparison of the average blade load of torque converter
进一步地,其叶表压力载荷对比结果如图12所示。
由图12 可知,压力载荷结果在起动工况下变得更加平滑,最高压力下降,同时压力均值增大,而设计工况中最大压力同样下降,压力梯度变得平缓,但其压差略小于原设计。
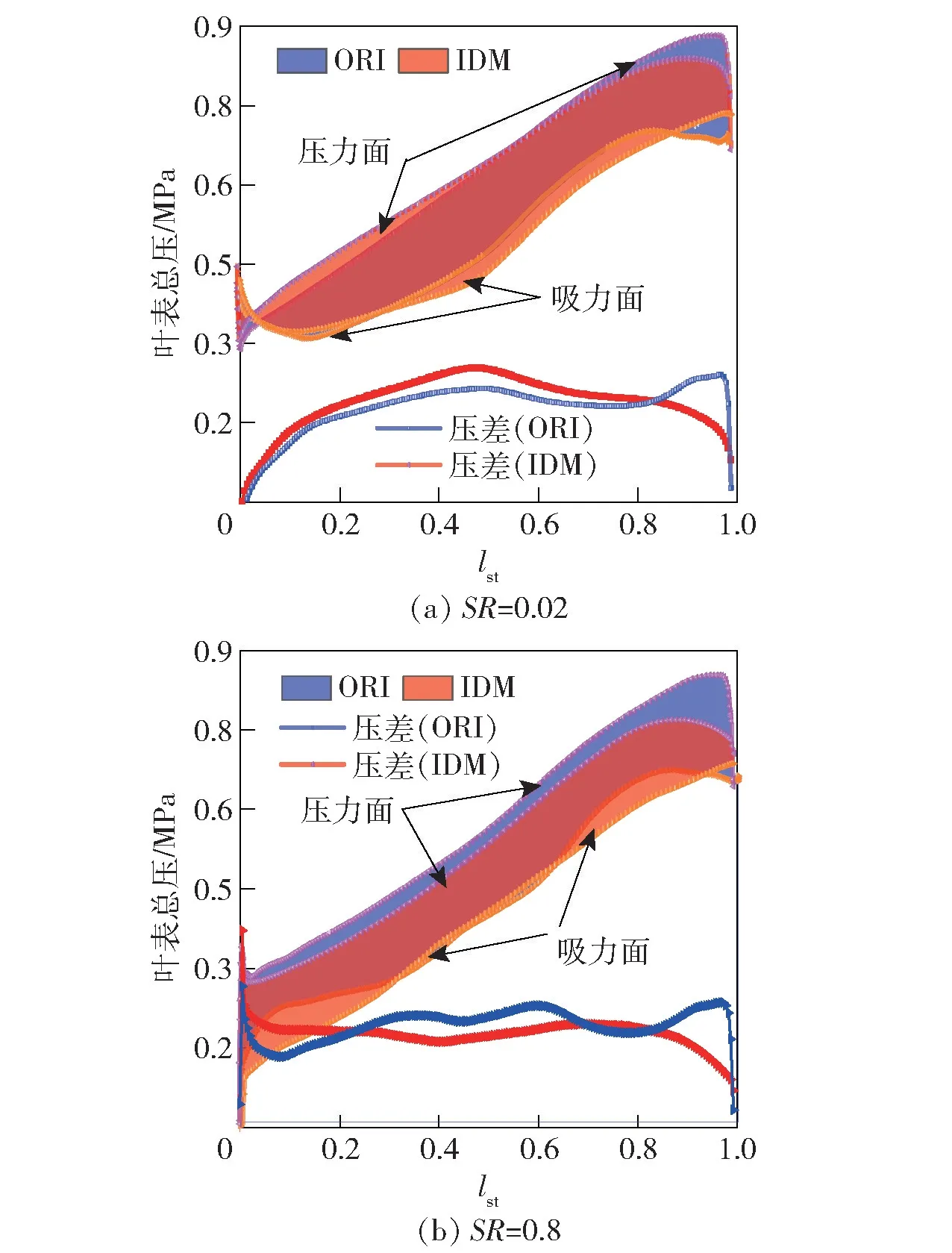
图12 优化前后叶表压力载荷结果Fig.12 Pressure difference near the blade before and after optimization
对入出口叶表载荷之差(动力载荷) 及其对应的性能响应进行统计分析,还可以得到图13 所示结果。由图13 可以看到,泵轮能容特性与动力载荷存在显著的二次相关关系,拟合结果表明动力载荷设计域不超过3.42 时动力载荷越大,反设计得到的泵轮转矩将越大,变矩器的能容特性也就越高。上述结果表明,对变矩器的能容性能进行高能容的定向设计在原理和设计中均可行且有效。
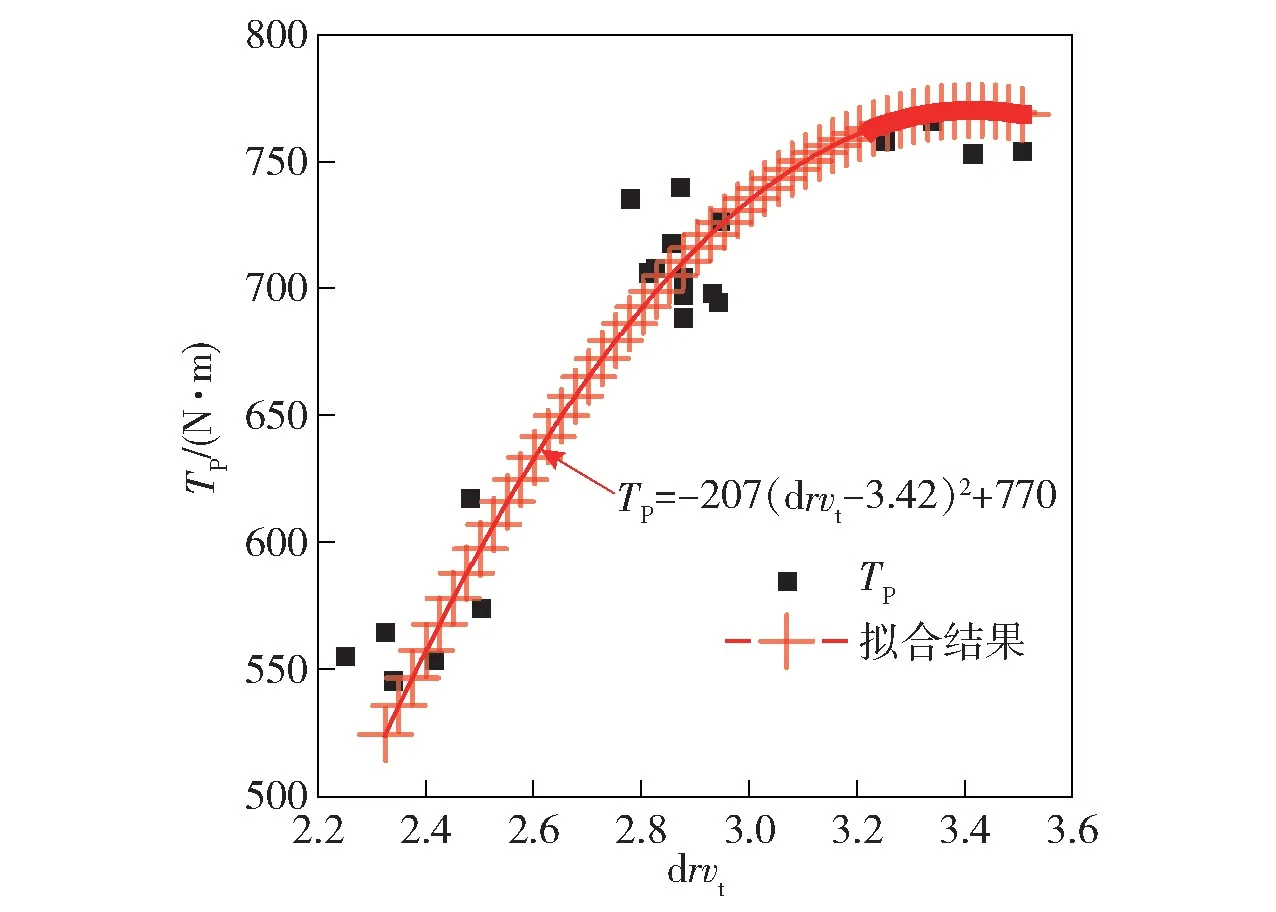
图13 动力载荷对泵轮转矩的关系Fig.13 Relationship between the dynamic load and the torque performance result of the impeller
4 结论
本文通过以质量平均周向速度矢量作为叶表载荷对叶片进行反设计的方法,并提出基于动力载荷对泵轮能容性能进行定向反设计。得到以下主要结论:
1) 通过rvt叶表载荷分布的设计可实现对液力元件叶片的有效反设计,案例中泵轮入口内环处动力载荷提升10%,实现了能容提升5.2%的提升,同时叶表载荷下降了4.9%。
2) 对于液力变矩器,泵轮动力载荷与能容存在显著二次相关关系,因此可通过提升动力载荷来定向提升变矩器的能容性能,泵轮的动力载荷越大,其能容性能越高。
3) 叶片动力载荷一定的情况下,通过对该流线位置的叶表载荷分布进行设计与优化,使得载荷分布梯度结果极大值降低,并缩小极值之间的差异,可以有效减少二次流,抑制空化以及降低液力损失,达到提升效率和改善流场平顺性的作用。
