基于代理模型进化的履带车辆动力学参数优化

张发平，张书畅，武锴，张云贺，阎艳

(1.北京理工大学 机械与车辆学院，北京 100081;2.北京电子工程总体研究所，北京 100085)

0 引言

坦克作为现代战争的主要路基武器载体，行进间射击精度和行驶平顺性是其重要的设计技术指标［1-3］，这些指标要通过对坦克动力学模型的参数优化来保证。基于虚拟样机技术的多体动力学建模仿真与参数优化是目前研究坦克等高机动履带车辆动力学性能的重要方法［4］。在进行参数优化时，需要大量重复调用仿真模型以获取响应计算目标值。然而由于该类车辆总体复杂，动力学仿真模型往往是高度密集计算、求解周期长、难以在有限计算资源内大量求解，成为制约参数优化效率和精度的瓶颈之一［5-6］。

使用代理模型技术构建设计变量和目标函数的近似响应面来提高优化效率，是现有研究的主流方向之一。如借助近似模型对履带车辆多体动力学模型的参数进行修正来解决模型仿真与试验结果的匹配问题［7-8］，基于全局敏感性分析采用代理模型对复杂非线性机械系统进行参数优化［9］等。然而，这些方法需要大量采样且优化精度不高，因此如何进一步提高效率和精度仍需研究。

基于代理模型的全局优化(SGO) 可以有效降低“昂贵模型”评估的次数，适用于包含高性能仿真模型的设计优化过程［10-11］。传统的SGO 方法需大量增加样本来降低代理模型的全局误差，很容易产生维度灾难问题。为了解决这一问题，近年来衍生出基于代理模型的全局抽样优化(SGSO) 方法，在SGO方法的基础上增加代理模型的静态和动态采样方法更新策略，在优化过程中选择样本点来更新代理模型。

更新抽样方法采用基于预测最优解的发掘方法［12］，将预测最优解作为新增样本点，通过提高代理模型的精度，来有效避免优化收敛得到非最优解。基于设计空间填充的采样策略，通过引入规则，将基于预测最优的发掘法和基于误差的发掘法融合。方法包括由Jones［13］提出的基于改善概率的全局优化(PGO) 算法和Jones 等［14］提出的基于期望改善度的全局优化(EGO) 算法，以及期望改善度(EI) 方法［15］。这些方法虽有较强的全局探索能力，但局部发掘性能较差，当各设计变量维数较高时收敛速度会大幅降低。

另外一类提高效率和精度的研究是基于设计空间缩减的策略方法。主要包括信赖域(TR) 方法和分割平面(CP) 方法。TR 法［16］提出TR 缩放指标，在每次迭代中根据缩放指标的大小判断设计空间是该收缩还是该扩张。Cheng 等［17］将TR 思想和模式采样(MPS) 方法结合，显著提高了MPS 的高维优化效率。TR 法求解局部最优解的效率较高，但在全局探索方面的能力稍显薄弱。CP 法由Wang 等［18］提出，其思想是通过设计空间中的超平面分割响应面，保留代理模型预测值较小的部分，并在该区域使用DOE 方法采集新的样本点，CP 的边界由最优化方法确定。CP 法是单向设计空间缩减法，无法增大寻优子空间，因此很可能陷入局部最优。

针对以上问题，本文以坦克动力学模型参数优化为研究对象，提出一种基于代理模型进化的参数优化方法，旨在确保优化精度的前提下大幅减少仿真模型调用次数，提高优化效率。首先，进行坦克机械系统拓扑关系及约束分析，建立坦克行进间多体动力学仿真模型;其次，以垂向加权加速度均方根与俯仰角加速度均方根组合构建目标函数，并选出对目标函数较敏感的设计变量;随后，提出基于代理模型进化的参数优化方法，在重点区域持续更新代理模型;最后，使用该方法进行模型参数优化，得到高精度代理模型和最佳参数组合。

1 坦克行进间多体动力学建模

1.1 坦克机械系统拓扑结构及约束建模

现代履带坦克部件众多，组成结构复杂，性能指标多。根据经验，在此选择影响性能的技术指标:车辆行驶的平顺性为主要成分［19-20］。忽略动力和传动系统，某型号坦克主要由上装系统和底盘行动系统两部分组成。上装系统通过上、下座圈与底盘系统连接。所构建的被动悬挂坦克行进间多体动力学模型共包含619 个部件、660 个约束。部件和约束明细见表1 和表2。根据部件之间的连接关系以及部件之间的约束状况，简化后的坦克机械系统拓扑结构图如图1 所示。这些零部间的约束共包含普通接触约束24 个，间隙碰撞接触约束12 个，接触摩擦184 个，刚度阻尼力矩18 个。其多体动力学模型的构建可通过理论方法描述约束力与状态变量间的关系。具体可用多体动力学仿真软件RecurDyn 进行建模仿真，通过添加直线弹簧阻尼器和扭转弹簧阻尼器实现各约束，其中直线弹簧阻尼器和扭转弹簧阻尼器的非线性刚度和阻尼特性数据设置为样条曲线。

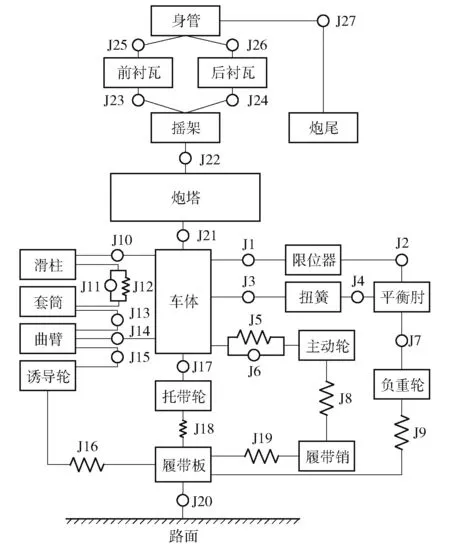
图1 坦克多体动力学模型拓扑结构图Fig.1 Topological structure of the multi-body dynamics model

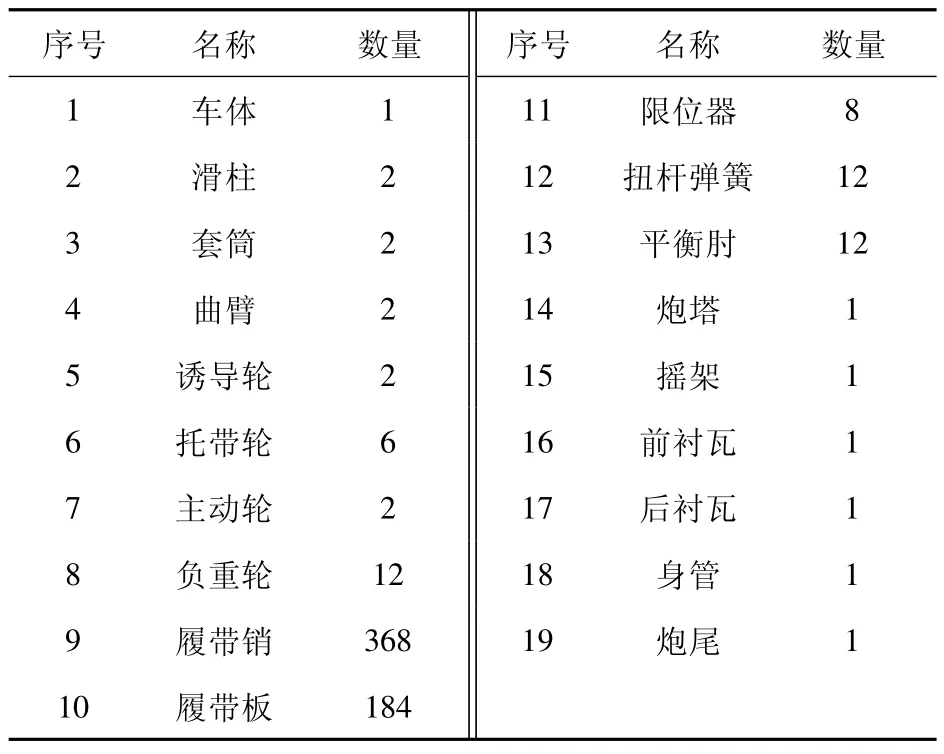
表1 坦克多体动力学模型部件明细Table 1 Details of tank multi-body dynamics model cemponents

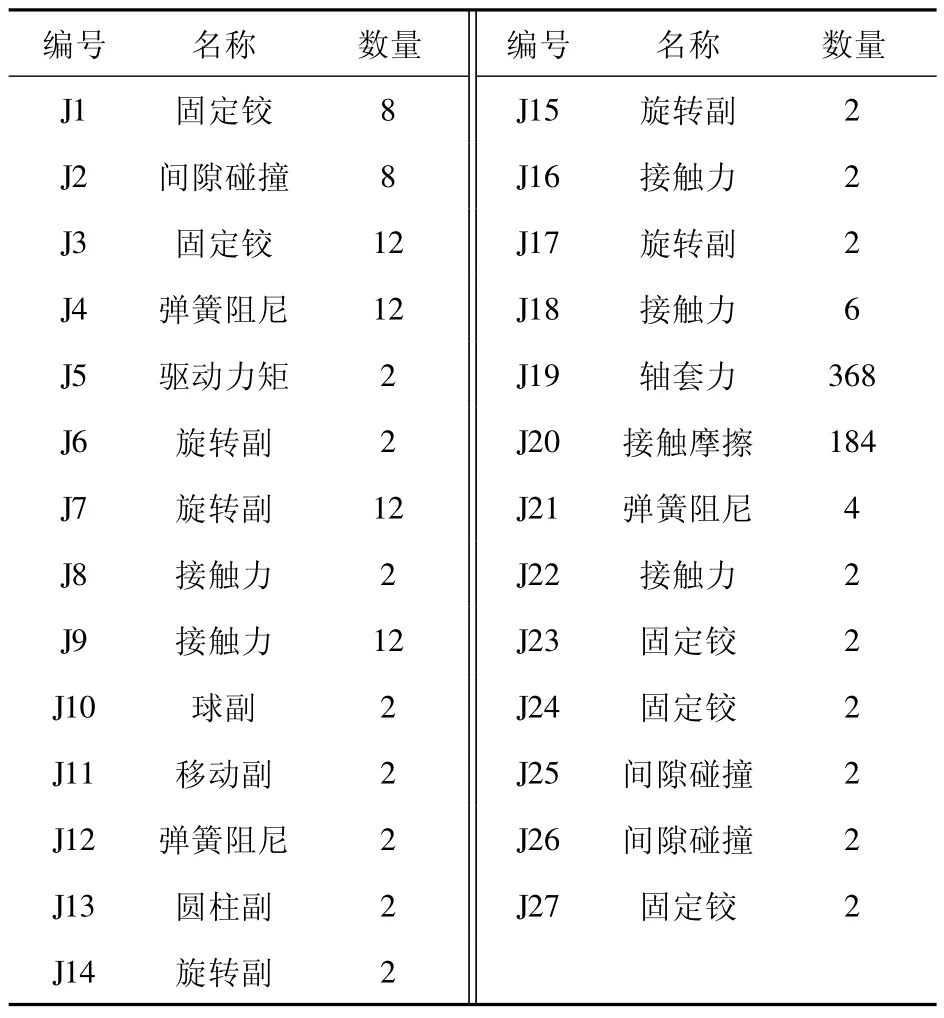
表2 坦克多体动力学模型约束明细Table 2 Constraint details of tank multi-body dynamics model

1.2 路面谱的三维不平度建模及包络效应处理

1.2.1 路面谱的三维不平度建模

坦克等履带车辆行驶过程中路面激励影响车辆的性能。根据国家标准GB7031—1986 车辆振动输入路面平度表示方法规定的路面不平度公式量化如下:

式中:Gq(n) 和Gq(n0) 分别为路面不平度功率谱密度和标准功率谱密度;n 为路面不平度空间频率;n0为其对应的标准空间频率;w 为路面功率谱密度的频率指数。一般采用谐波叠加法［10］建立如下三级路谱。左右相干路面不平度表达式如下:

式中:ql(x) 和qr(x) 分别为左、右路面不平度表达式;ni为将空间频率nmin＜n ＜nmax平均划分为N 个区间中第i 个区间的中心频率;αl为［0，1］区间内的随机数，表示左侧相位系数;αr为右侧相位系数，决定了左右两侧的相干性，其计算由相位角拟合，见文献［21］;d 为负重轮轮距;αn为［0，1］区间内的随机数;Ai表示谐波振动幅值，

Gq(ni) 为功率谱密度，可以由国家标准GB7031 进行计算得到，Δn 为空间频率间隔。

GB7031 根据功率谱密度将路面划分为A～H 8 个等级，H 级的平度系数的几何平均值最大，为262 144，代表等级中最严苛的路面。因此，本文建立D、F、H 三个等级路谱，分别代表不同路面不平度的等级进行仿真，如图2 所示。

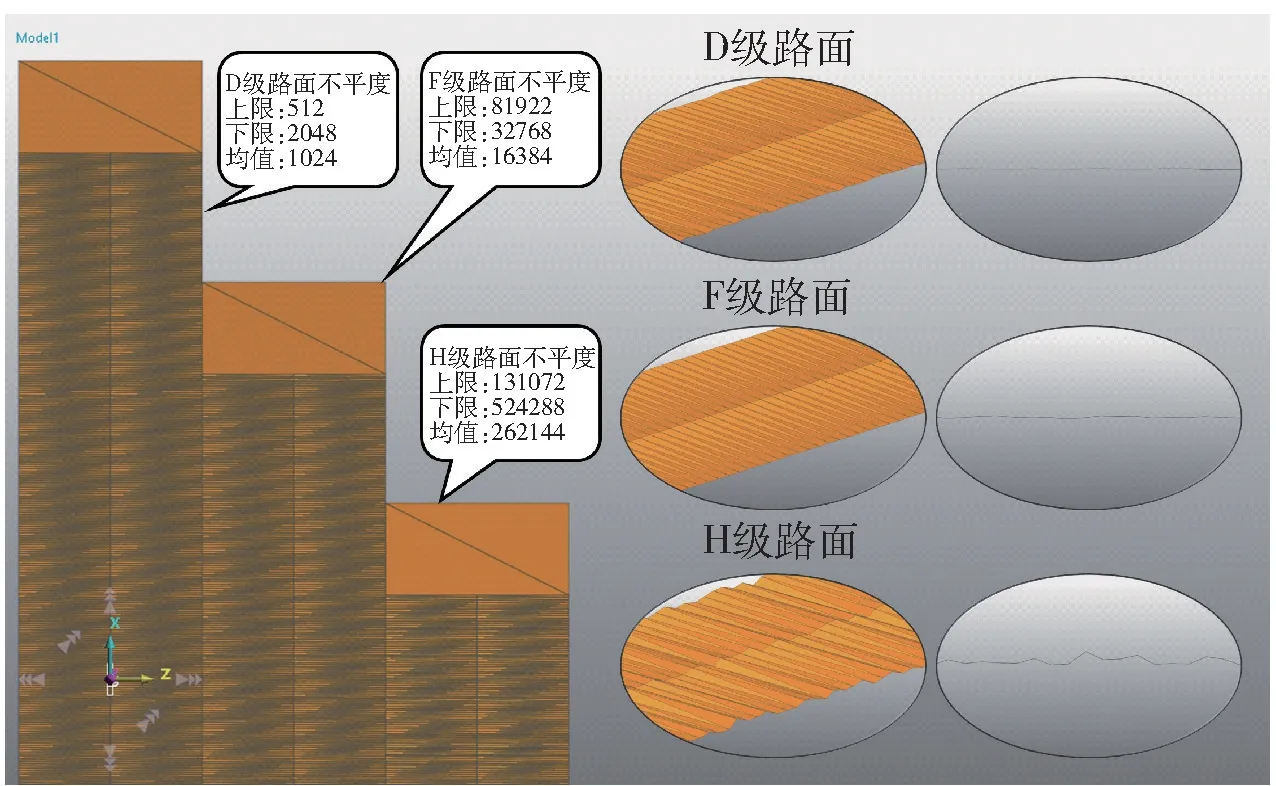
图2 D、F、H 级路面左右相干三维不平度模型Fig.2 Left-right coherent three-dimensional roughness model of class D，F and H pavements

1.2.2 履带板包络效应的路面谱滤波建模

履带装甲车辆在路面行驶时，因履带板对地面具有包络效应，作用在负重轮上的高程激励发生变化。可以将履带对地面的滤波作用等效成1 阶低通滤波器对路面谱的作用，标准形式为

式中:G(ω) 为滤波器幅频特性，ω 为路面激励频率;G0为零频增益;ωc为滤波器截止角频率;G(n) 为履带滤波函数;S0为静态灵敏度;nc为空间截止频率。履带对地面的滤波函数与自身结构和车速有关。通过相应等级的路面不平度和对应车速下滤波函数对位移谱进行滤波，得到时域信号作为去履带后的路面激励输入，对履带车辆悬挂系统做动态特性分析。

1.3 坦克整车多体动力学仿真模型

基于机械系统部件拓扑关系及约束模型，采用多体动力学仿真软件RecurDyn 建立坦克行进间多体动力学模型。所构建的整车RecurDyn 模型如图3 所示。

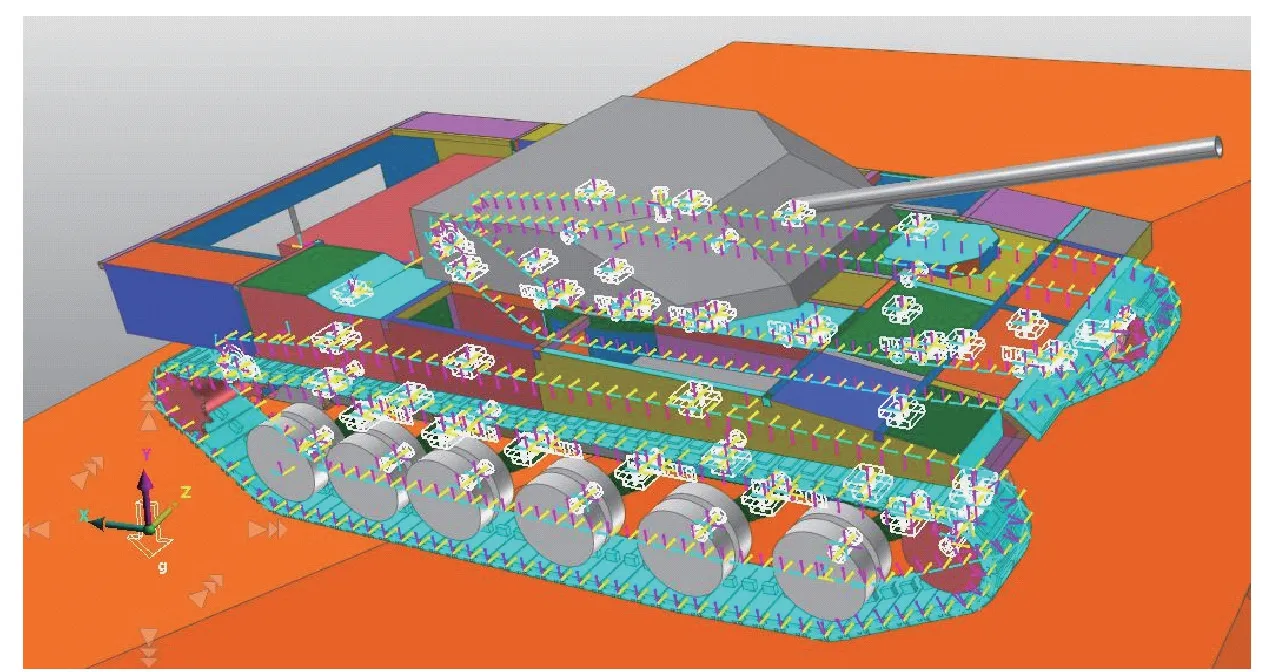
图3 坦克整车多体动力学RecurDyn 模型Fig.3 Tank multi-body dynamics RecurDyn model

2 悬挂系统参数优化目标函数及变量确定

2.1 悬挂系统参数优化目标函数

坦克等履带车辆行驶过程中，驾驶舱地板位置的垂向加速度和坦克车体的俯仰角加速度是重要的评价指标［20，22-23］，因此将坦克在不同路面上行驶过程中车体驾驶舱位置的垂向加速度均方根aya和俯仰角加速度均方根值azw加权，作为车辆性能综合指标，共同组成如下优化目标函数:

式中:wya和wzw分别为两者的权重，用来平衡两目标项的数量级。该目标函数没有具体物理意义，只是保证两者之和的最小化。目标函数的取值越小，车辆行进间的综合性能越好。

垂向加速度均方根aya和俯仰角加速度均方根值azw的计算根据国际标准ISO 2631-1:1997 人体承受全身振动评价进行，此标准认为人体对0.5～80 Hz区间的不同频率振动的敏感程度不同。因此采用加权加速度均方根值对舒适性进行量化，通过快速傅里叶变换(FFT) 将仿真得到的驾驶舱位置垂向加速度时域谱变换为功率谱

式中:Ga(f) 为垂向加速度频率谱;aya(t) 为垂向加速度时域谱。在此基础上，通过ISO2631-1 规定的0.5～80 Hz 区间频率加权函数对频谱加权，计算均方根值如下:

式中:F 为总频率尺度;ω(f) 为频率分段加权函数:

联合式(7)～式(8)，可以得到垂向加权加速度功率谱密度。

坦克车体的俯仰角加速度时域均方根值量化计算方法如下:

式中:azw(t) 为车体俯仰角加速度时域谱;T 为总时间历程。

工程上这些参数均通过坦克车辆主动悬挂系统的设计参数或控制参数来控制，因此选择悬挂系统参数作为优化变量来进行优化。

2.2 悬挂系统参数优化设计变量

坦克等履带车辆的参数优化效率受设计变量的维度和设计空间的影响，高维度的设计变量和大尺寸的设计空间常常导致计算成本骤升。因此为了提高优化效率，根据车辆动力学相关理论，选择6 个对目标函数敏感的悬挂系统参数作为设计变量来控制设计变量维度，分别为:左右两侧1、6 号扭杆弹簧刚度系数，左右两侧2、5 号扭杆弹簧刚度系数，左右两侧3、4 号扭杆弹簧刚度系数，左右两侧1、6 号扭杆弹簧阻尼系数，左右两侧2、5 号扭杆弹簧阻尼系数;左右两侧3、4 号扭杆弹簧阻尼系数。另一方面，通过基于代理模型进化的参数优化方法在参数优化过程种持续缩小设计空间尺寸，节约计算资源，提高优化效率。6 个设计变量的位置示意图如图4 所示。图4 中，a1～a6分别为相应车轮间的水平距离，mb为车体质量，zb为车体的垂向位移，zw1～zw6分别为相应车轮相的垂向位移，zt1～zt6分别为相应车轮位置处路面的激励位移。

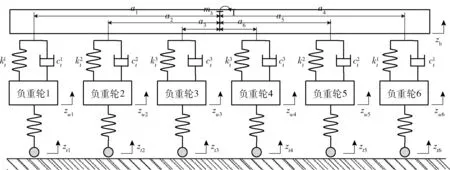
图4 优化变量位置示意图Fig.4 Schematic diagram of optimized variable location

王钦龙等［8］在履带车辆模型修正工作中通过极差法确定了对目标函数较敏感的设计变量分别是车体俯仰转动惯量Izz、悬挂系统刚度k 和悬挂系统阻尼c。车体转动惯量Izz受整车各部件质量、质心等多因素影响，不具备优化价值。

2.3 悬挂系统参数优化联合仿真过程

基于代理模型进化优化算法的履带车辆参数优化过程由算法程序、控制程序和坦克行进间多体动力学模型联合仿真环节所组成。其中，算法程序为采用MATLAB 软件自研的代理模型进化优化算法，控制程序依托Simulink 由RecurDyn 联合仿真模块和其他基础组件构成，实现坦克行进间多体动力学模型的参数传入和响应采集功能，以动力学仿真软件RecurDyn 为基础平台，根据第1 节提供的机械系统拓扑及约束信息实现坦克行进间多体动力学模型建模，以及3 种三维路面谱建模和行进动力学仿真。具体结构如图5 所示。

3 初始代理模型构建

坦克行进间多体动力学仿真模型部件及约束众多，单次仿真求解效率极低(本文仿真配置计算机下一次仿真约20 min) 。为解决该问题，本节将构建初始代理模型表征设计参数和目标函数之间的响应关系，为基于代理模型进化的参数优化方法确定优化搜索方向。

初始训练样本集的空间均布性决定了初始代理模型能否有效地表征设计变量和目标值在整个设计空间的响应面关系。针对2.2 节给出的坦克优化设计变量及对应的可行空间，使用基于随机进化算法的最优拉丁立方(ESEA-OLHD) 法进行试验设计，获得6D(D 为设计变量维度) 个样本，通过2.3 节联合仿真计算得到响应，生成初始训练集。使用扩展径向基函数(RBF) 代理模型［24］构建6 维设计变量与目标之间的初始响应面。扩展RBF 代理模型详细过程见文献［11］。

在D、F、H 三个等级路面条件下，ESEA-OLHD试验设计法采样获得训练样本集，据此构建三级路面6 维设计变量和目标函数间的初始代理模型，如图6 所示为以图形方式表示的初始代理模型，因篇幅原因只列出D 级路面。图6 中，K1为设计变量中的刚度，C1为设计变量中的阻尼。初始代理模型将在优化过程中持续更新，不断提高拟合精度。

4 基于代理模型进化的参数优化方法

为了解决传统工程设计优化问题大量调用仿真模型导致的优化效率低问题，本文提出设计空间的三层分解方案、基于代理模型进化的参数优化方法，以及在可能最优解的重点区域的代理模型动态更新，从而提高优化精度，降低样本使用量。

4.1 多层设计空间缩减策略

在工程设计优化初始阶段，设计变量范围设定往往较大，以便能覆盖所有可能的设计结果，但带来的后果是大设计范围导致空间搜索成本过高。本节将设计变量所构成的空间划分为三层空间，分别为初始设计空间(OA)、局部过渡子空间(MA) 和重要子空间(IA) 。各子空间关系示意图如图7 所示。

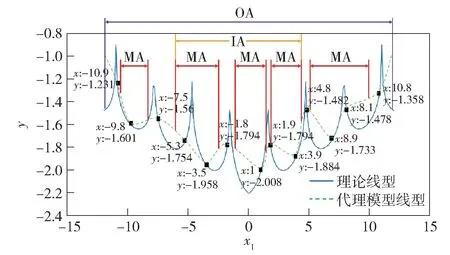
图7 某次迭代过程中三层子空间示意图Fig.7 Schematic diagram of three-layer subspaces in an iterative process

4.1.1 初始设计空间(OA)

OA 是优化变量的初始范围，也是首次迭代的基准空间，覆盖变量所有可能取值。在OA 空间中通过极值法和高斯误差法的动态采样策略，可以改善代理模型在整个初始设计空间的精度，通过基于ADAM 梯度下降的局部寻优法和松弛判别式寻找可能被遗漏的极小值，为算法提供跳出局部最优解的能力。

4.1.2 局部过渡子空间(MA)

MA 是过渡子空间，可由图8 所示的二次聚类法把OA 划分为多个子MA 空间。每一个MA 空间包含优化问题的一个或多个局部极小值。在各MA空间中，采用ADAM 梯度下降法寻找MA 空间中的局部极小值并更新代理模型，确定本次迭代的预测最优解。

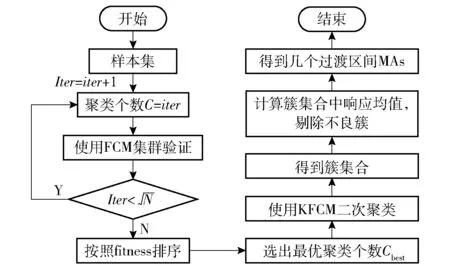
图8 基于二次聚类确定过渡区间流程图Fig.8 Flow chart of determining transition intervals based on quadratic clustering

使用确定MA 子空间的步骤如下:

1) 首次聚类种群验证。通过基准空间样本点数量确定聚类数量区间，以区间中的每一个取值为先验值，执行模糊C 均值(FCM) 聚类，计算每一次聚类结果的评价指标，衡量聚类种群的有效性。将评价指标最优的聚类数量值作为最佳聚类数量，并保存最佳聚类中心坐标。

2) 二次聚类划分种群。以最佳聚类数量和最佳聚类中心坐标为先验条件，对样本集进行基于核函数的模糊C 均值(KFCM) 聚类，得到cbest个簇，每个簇都包含局部极小值。选择平均响应较低的前50%(根据经验取值) 簇作为各MA 子空间，根据各簇包含样本各维坐标的最大、最小值确定子空间范围。文献［25 -26］提供了FCM 和KFCM 的详细执行过程。

4.1.3 重要子空间(IA)

IA 是最可能包含全局最优解的区域，是设计空间的进一步收缩。通过ADAM 梯度下降法在IA 子空间中开展优化搜索工作，使用基于极值法和高斯误差联合采样策略在IA 子空间中重点采样，在可能存在全局最优解的邻域深入探索并持续精化代理模型。确定IA 的具体操作步骤如下:

1) 通过二次聚类法确定若干过渡空间MA;

2) 对所有MA 空间中的局部最小值排序，得到最佳预测值作为IA 子空间的中心;

3) 以IA 空间隶属的MA 子空间边界和最佳预测值的各维度坐标为依据，计算IA 子空间各维度边界。MA 数量大于1 或等于1 两种情况下IA 区间边界IA_range 的计算方法如下:

式中:prebest为当前最优预测值所在点的各维度坐标向量;MAurapnge和MAlroawnge分别为MA 空间各维度上界和下界;size(MA) 为MA 空间的数量。通过在IA 子空间中进行多种形式，更多数量的采样，提高代理模型在该区域的精度，进而促进全局最优解的捕获，且IA 区间的范围相对于MA 区间得到了进一步缩减。多层空间缩减的算法伪代码见附录1。

4) 根据搜索效率和精度的综合考虑，每3 次迭代后进行IA 空间确定，防止过早收敛。

4.2 多起点局部寻优及代理模型动态更新

4.2.1 基于ADAM 梯度下降法的局部寻优

优化迭代过程中，需要在MA 和IA 子空间进行局部寻优，获得局部极小值、确定新增样本点，更新代理模型。使用用于深度学习的ADAM 梯度下降法［27］，从多个起点进行搜索来捕获空间中的多个局部极小值。

在MA 空间和IA 空间执行基于ADAM 的局部寻优算法，流程见附录2。需将寻优搜索限制在MA或IA 空间范围中，在搜索过程中接近上下边界的变量维度将停留在边界，其他维度依然保持向负梯度方向搜索，直至到达预设最大迭代次数stepnum或满足收敛条件‖deltaX‖2＜ε，ε 为一个足够小的值，一般取ε×10-8。

4.2.2 基于动态采样策略的代理模型更新

新增样本点是优化迭代进程中代理模型更新的重要来源，本节提出基于极值法和高斯误差法联合的动态采样策略。

4.2.2.1 基于极值法的新增样本点

该方法将获得子空间中可能是全局最优点的候选点，执行步骤如下:

步骤1确定各空间(如MA) 包含的观测样本点集以及边界。

步骤2在空间边界内从多起点进行ADAM 梯度下降搜索，得到各子空间内所有局部极小值，将其按预测响应从小到大排序后取各子空间前p 个局部极小值，p 的取值如下:

式中:s 为本次迭代生成的子空间数量。需要说明的是，p 和s 的取值是考虑到效率精度的平衡。

步骤3剔除新增样本点集中的两类冗余:1) 从多起始点搜索得到的局部极小值可能收敛到同一位置;2) 得到的新增样本点可能与原有样本集中的点重合。对此，计算新增样本点集中各点欧式距离，剔除距离相近的新增样本点;逐一计算新增样本集和原始观测样本集的欧氏距离，剔除冗余点。欧式距离评价公式如下:

式中:x1、x2为两个样本点;‖＊‖2为向量L2 范数;LHSrange(1，:) 和LHSrange(2，:) 分别为初始设计空间各维度的上界和下界。

4.2.2.2 基于高斯误差法加点

该方法将获得该次迭代关注区域内代理模型误差较大位置的样本点。高斯误差的计算包含三部分:1) 利用空间(如IA) 样本集训练该区域的高斯过程回归模型(GRF)，得出IA 空间各处高斯过程预测值IA_GRF_pre 和方差σ;2) 计算IA 子空间各处GRF 和RBF 预测响应偏差Δpre=|IA_GRF_pre-IA_RBF_pre|;3) 分别将高斯过程方差和预测响应偏差进行标准化:

式中:σnor为标准化方差;Δprenor为预测响应偏差。以上两个参数加权，得到总误差值SE=0.2Δprenor+0.8σnor，选择总误差值最小的3 个点作为新增样本集。

高斯过程方差和高斯过程回归模型的理论内容见文献［28］。优化迭代中动态采样策略在MA 和IA 子空间采样流程见附录1 的多层空间缩减策略算法和附录2 的基于ADAM 梯度下降的局部寻优法算法。

4.3 基于动态采样的局部最优解跳出

在满足判别标准下在OA 空间中使用动态采样法更新代理模型避免算法陷入局部最优解，伪代码如附录3，分为以下4 个步骤:

步骤1执行判断:若某次迭代新增样本点为0或观测最优值连续3 次迭代中没有发生变化，则判定当前迭代过程是否陷入局部最优。

步骤2执行动态采样:在OA 中执行高斯误差采样和极值采样，得到预测响应误差较大和局部最优位置的新增样本点。

步骤3更新基准空间:若OA 中最小的局部极小值OAbest与当前全局最优解prebest(iter) (iter 为迭代次数) 满足松弛判别式(11)，则更新全局最优解，合并基准空间OAbest的坐标作为下次迭代基准空间边界。

4.4 优化流程

基于代理模型进化的参数优化方法流程如图9所示。流程包含4 个部分:1) 循环迭代前，初始化参数并训练初始代理模型;2) 进入迭代后，使用多层空间缩减策略确定三类子空间，并从三类子空间中交替局部寻优并获取新增样本点;3) 执行跳出局部最优解的措施，确定新增样本集;4) 更新基准空间和代理模型，计算目标值并判断是否终止。

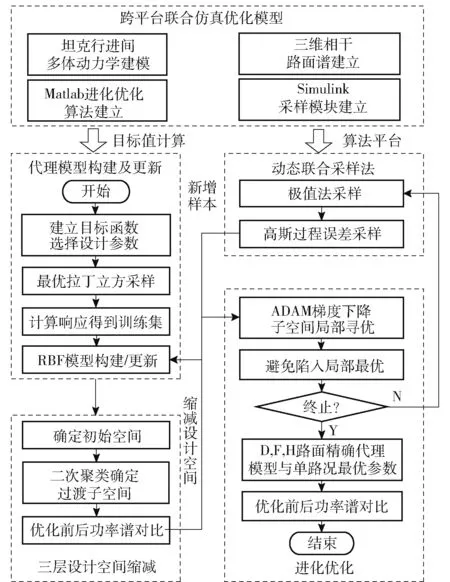
图9 坦克参数优化总体技术流程Fig.9 Overall technical process of tank parameter optimization

5 基于进化优化算法的悬挂系统参数优化

5.1 坦克悬挂系统设计参数优化过程

分别针对D 级、F 级和H 级3 种道路环境进行基于代理模型进化的参数优化，以尽可能少的样本得到单路面情况下的最佳设计变量组合以及单路面情况下设计变量和目标值的高精度响应面。其中，D 级路面优化问题的数学表达式如下:

在本文优化问题中，多层设计空间缩减策略、基于代理模型进化的参数优化方法各子方法参数以及RecurDyn 行进间多体模型仿真参数设置如表1 所示。

表1 优化过程中算法及仿真模型参数设置Table 1 Algorithm and simulation model parameter setting

5.2 3 种路面条件的优化结果分析

图10 为D 级路面10 次优化中最小全局最优解的收敛曲线。由图10 可知，每3 次迭代目标值有较大幅度下降，第8～13 次迭代中陷入局部最优，算法采取相应策略跳出局部最优，于14 次迭代中得到更小的目标值。表2 所示为10 次优化中坦克在D 级、F 级和H 级路面下优化前后悬挂系统参数优化的目标值，变化率分别为［27.2%，34.8%］、［23.3%，26.6%］、［19.6%，21.3%］，样本使用量分别为［91，108］、［91，110］、［93，109］。表3 为优化前后的参数值。表2 表明，该方法的优化参数可使得3 种路面下行进间车辆性能综合指标平均提升分别为32.4%、24.5%和20.4%，且可综合将传统方法平均样本使用量的约500～1 000 次降低到80～150 次，在同等算力下节省时间100 h 以上(以本文所用计算机配置单次仿真周期20 min 计算) 。

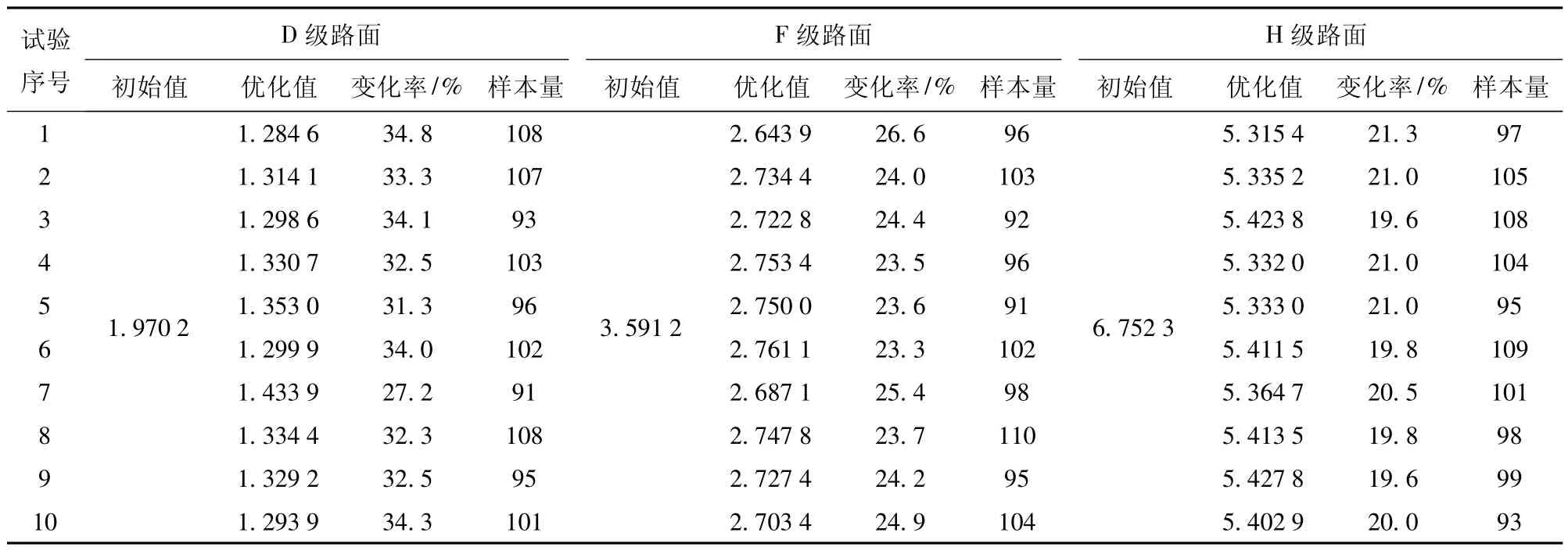
表2 基于代理模型进化优化算法的10 次单路面优化(悬挂系统参数优化目标函数值)Table 2 10 times single road optimization based on agent model evolutionary optimization algorithm(objective function value of suspension parameter optimization)

表3 3 种路面下的最优参数组合Table 3 Optimal parameter combination for each grade of pavement

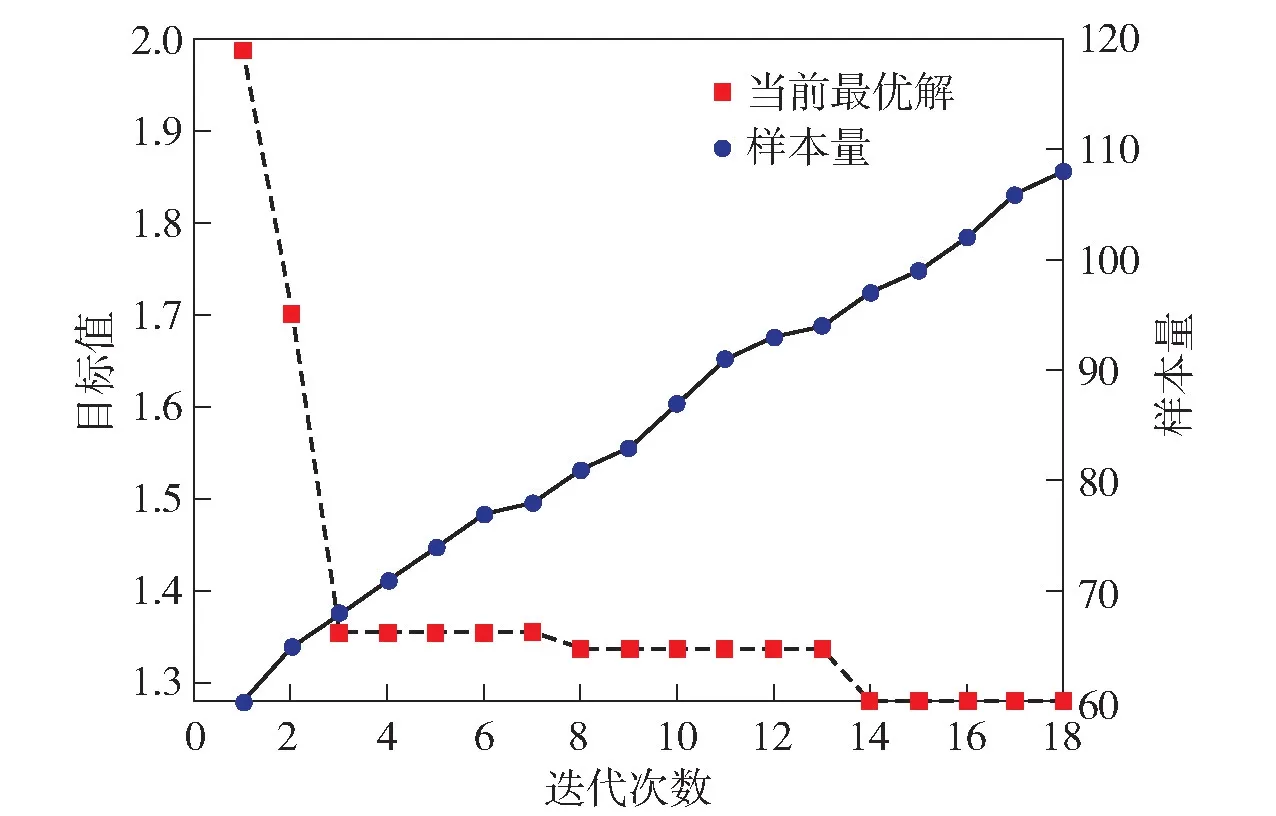
图10 D 级路面谱优化收敛曲线Fig.10 Convergence curve of spectrum optimization of grade D pavement

使用H 级路面下的最优参数组合和初始参数组合进行仿真，得到坦克行进间加速度功率谱对比曲线如图11 所示，从中可以看出优化后0～50 Hz振动频率区间内功率谱密度均值和极值都有了显著降低。

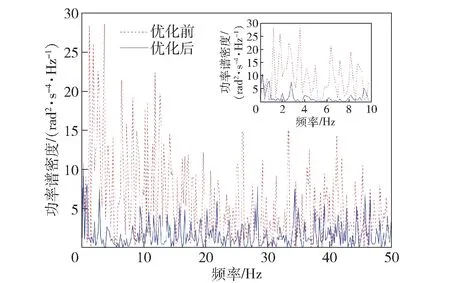
图11 H 级路面下优化前后功率谱密度对比Fig.11 Comparison of power spectral densities before and after optimization for H grades of pavement

6 结论

本文以履带车辆多体动力学模型参数优化为研究对象，提出了基于代理模型进化算法的参数优化方法，以提高复杂多体动力学系统优化的效率，并用悬挂系统的参数优化进行了验证。得出主要结论如下:

1) 提出了复杂结构履带车辆动力学参数优化的代理模型进化优化方法，可实现异构模型间信息无缝传递，以及代理模型进化和参数优化的有效融合，提高了参数优化的精度和优化过程的效率。

2) 在3 种路面下对坦克动力学数值仿真的结果表明，本文提出的基于代理模型进化的参数优化方法与传统优化方法相比，优化精度提高21.3%，降低样本使用量31.5%。同时，该方法的优化参数可使得3 种路面下行进间车辆性能综合指标平均提升分别为32.4%、24.5%和20.4%。

3) 本文优化方法本质上是一种单目标优化法，在求解多目标优化问题时，需要通过权重分配系数建出单目标代理模型后再求解。下一步研究中将引入多目标概率期望改善等方法，使算法具有本质多目标优化能力，并结合具体的工程实际验证。

附录1

多层空间缩减策略算法

Begin

初始化:初始采样个数m 和维度D，其中样本个数m 推荐的数量为二维问题［20，40］，当维度2 ＜n ＜10 时，推荐采样数量为［6n，8n］;n ＞10 时推荐［50，70］;RBF 代理模型及训练迭代次数为80，初始各个维度可行设计空间为LHSrange;

得到昂贵初始样本集:

Xolh 优化拉丁超立方采样在LHSrange 中得到样本点矩阵mxD

Yexp 通过复杂模型计算初始样本集Xolh 的目标值，即响应值，矩阵大小为m×1

Sexp 将初始样本点坐标和其对应的响应值合并为初始昂贵样本集矩阵，大小为m×(D+1)划分训练集和测试集:

Sexp_train 和Sexp_test 通过留一交叉验证法将初始昂贵样本集划分为训练集和验证集，用来更高精度地训练代理模型

训练代理模型:

RBF(Sexp_train，Sexp_test) 训练RBF 神经网络作为代理模型，并通过交叉验证提高代理模型精度

save NET_RBF_iter1.mat-mat net 保存该次迭代过程中训练好的代理模型

End

空间缩减:

Input: Sexp，NET_RBF_iter1.mat，iter

初始化: FCM 和KFCM 最大迭代次数为100，终止条件为1 ×10-5，KFCM 使用高斯核函数，参数sigma 设置为150;

MA——首先进行二次聚类，划分种群过后进行一定筛选工作，得到s 个MA

Two-stage clustering:

Cbest——最佳聚类个数

Para_miu_best——种群验证后得到的与最佳聚类个数对应的聚类中心

Label_KFCM——得到种群划分矩阵，存储类表标识，数据点坐标以及观测响应

The determination of MA——将二阶段聚类得到的种群通过响应值的大小进行排序，根据最小响应值从小到大的顺序将所有种群排序，取前20%的s 个种群作为s 个过渡区间。如果种群数量小于5，则只选出1 个种群作为MA。

MA_plt——得到每个过渡区间包含的样本点

MA_range——得到每个过渡区间对应的可行空间范围

IA——在确定MA 的基础上，通过分层寻优法判断哪个空间是IA 空间

The determination of MA——确定s 个过渡区间以及响应的样本点和空间范围

分层寻优法——通过分层寻优法寻找局部极小值

Local_min_MA——得到每个过渡区间内的局部极小值

The determination of IA

IA_plt——得到重要空间包含的所有样本点

IA_best——得到重要空间的最佳预测值

ImpAre_range——得到重要空间的区间范围

Output: MA_plt and MA_range/IA_plt，IA_best and ImpAre_range

End

附录2

基于ADAM 梯度下降的局部寻优法算法

初始化:学习率，最大迭代步长，初始参数，衰减速率

Input:

MA_plt and MA_range/ IA_plt and ImpAre_range——MA

空间或IA 空间包含的样本点以及对应的空间范围，假设某一空间中包含样本点S 个

NET_RBF_iter.mat——本次迭代训练的RBF 模型

Whileiter_opt ＜step_num——设置最大循环次数为step_num

grad——计算数值梯度

Square gradient——累积平方梯度

更新参数

deltaX=-grad* 学习率——计算该次迭代的样本点各维坐标增量

Xiter_opt+1=xiter_opt +deltaX() ——更新寻优样本点的坐标

If ‖deltaX‖2＜1 ×10-8——所有维度增量都小于1 -e8，终止循环

Break;

End if

End while

Output: Local_min——得到大小为S×(D+1) 的局部极小值矩阵

End

附录3

优化流程及跳出局部最优策略算法总体迭代流程

While iter ＜itermax——进入循环体，itermax 为最大迭代次数

Iter=Iter++——迭代次数+1

If mod (iter，3)==0——如果当前迭代次数iter 是3 的整数倍

IA_plt，IA_best，BS_range——执行多层空间缩减算法，得到重要空间IA，下次迭代基准空间以及包含的观测样本点

Sample_best——执行基于极值的加点方法，得到包含可能全局最优点的新增样本点

Sample_gua——执行高斯误差加点，得到IA 空间误差较大区域的新增样本点

Sample_new——合并Sample_best 和Sample_gua 后，执行样本点筛选方法，剔除内外部距离过近的样本，得到最终新增样本集

Else

MA_plt，BS_range——执行多层空间缩减算法，得到过渡空间MA

Sample_best——执行基于极值的加点方法

Sample_new——执行样本点筛选方法

判断并执行未知区域探索部分

If iter ＞5——5 次迭代后，计算当前最优预测值和前5 次最优预测值的差CRT

CRT=Pre_best(iter) -Pre_best(iter-5)

Else

CRT=1 ×1010

End if

If size(Sample_new)=0 or CRT ＜1 ×10-6——如果本次迭代过生成新增样本点个数为0 或CRT 小于阈值

执行稀疏采样方法在OA 中采样

Sample_OA——OA 空间中执行高斯误差采样，生成新增样本点

OA_best——OA 空间中部分观测点为起始点使用寻优方法确定OA 最优预测值

Sample_new=［Sample_new;Sample_OA］——合并新增样本点

If OA_best-pre_best(iter) ＜pre_best(iter)/pre_best(1)

Pre_best(iter)=OA_best——更新最优预测值

BS_range——扩大并更新下次迭代基准空间

Sample_new=［Sample_new;Sample_OA;OA_best］——合并新增样本点

End if

End if

Sample_new_rdc——对新增样本点集执行去冗余操作，生成无冗余样本矩阵

Ysample_new——使用复杂模型计算新增样本点的观测值

Sexp——［Sexp;［Sample_new_rdc，Ysample_new］］将新增样本坐标和响应合并到整体样本集中

NET_RBF_iter+1.mat 更新RBF 代理模型

End While

Out put:pre_best，RBF——最终输出最优解以及最终RBF 代理模型