Multiple Nontrivial Solutions for Superlinear Double Phase Problems Via Morse Theory∗

Bin GEBeilei ZHANGWenshuo YUAN

Abstract The aim of this paper is the study of a double phase problems involving superlinear nonlinearities with a growth that need not satisfy the Ambrosetti-Rabinowitz condition.Using variational tools together with suitable truncation and minimax techniques with Morse theory,the authors prove the existence of one and three nontrivial weak solutions, respectively.

Keywords Double phase problems, Musielak-Orlicz space, Variational method,Critical groups, Nonlinear regularity, Multiple solution

1 Introduction and Main Results

The study of differential equations and variational probl ems with double phase operator is a new and interesting topic.Such problems go back to Zhikov [1–3] who introduced such classes of operators to describe models of strongly anisotropic materials and also the monograph of Zhikov-Kozlov-Oleinik[4].The main idea was the introduction of the functional

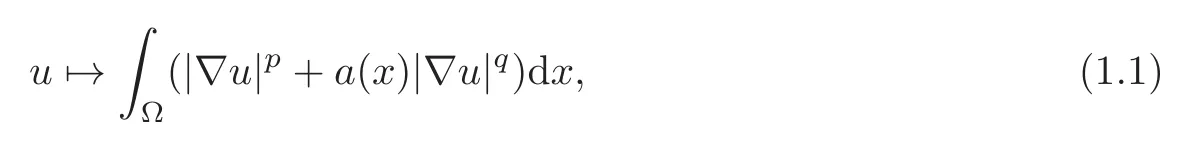
where the integrand switches two different elliptic behaviors.More precisely,energies of the form(1.1)are used in the context of homogenization and elasticity and the modulating coefficienta(·)dictates the geometry of a composite of two different materials with distinct power hardening exponentspandq(see [4]).Significant progresses were recently achieved in the framework of regularity results for quasi-minimizer or minimizers of such functionals, see e.g., [5–12].

The purpose of this paper is to investigate the existence and multiplicity of solutions for the following double phase problem

where Ω ⊂RNis a bounded domain with aC2-boundary∂Ω,N≥2, 1

andf:Ω×RR is a Carathéodory function satisfying the following conditions:

(f1)f(x,t)=o(|t|q−2t) ast→0 uniformly inx∈Ω.

(f2) There existq

(f3)uniformly inx∈Ω, where

(f4) If F(x,t)=f(x,t)t−qF(x,t), then there existsg∈L1(Ω) satisfying

The solution of (P) is understood in the weak sense, that is,u∈(Ω) is a solution of problem (P) if it satisfies

where(Ω) will be defined in Section 2.

Note that energy functional associated to (P) is denoted by

It is a well-known consequence of(f1)and(f2)thatϕ∈C1((Ω),R)and the critical points ofϕare weak solutions of (P).

Existence and multiplicity results for problems of type (P) have been discussed precisely by several authors.Especially Perera et al.[13] considered a double-phase problem with theq-superlinear reaction term, that is,

whereλ∈R is a parameter,q

for somep < σ < ρ < randC >0.In particular, applying the Morse theory, they proved the existence of a solution of problem (P1).Following this, Liu-Dai [14] considered the same problems for more general reaction term,and proved existence and multiplicity results,also signchanging solutions.Furthermore, we refer to a recent work[15] which shows the existence of at least three solutions of problem(P)by using strong maximum principle.A similar treatment has been recently done by Hou-Ge-Zhang-Wang [16] via the Nehari manifold method.Eigenvalue problems for double phase operators with Dirichlet boundary condition are also investigated in[17] , where the authors proved the existence and properties of related variational eigenvalues.For other existence results on elliptic equations with double phase operators we refer to the papers of Ge-Lv-Lu[18],Ge-Chen[19],Ge-Wang-Lu[20],Papageorgiou-Radulescu-Repovs[21–22], Radulescu [23], Cencelj-Radulescu-Repovs [24], Gasinski-Winkert [25–26], Zeng-Gasinski-Winkert-Bai [27] and the references therein.

Motivated by the aforementioned works,in the present paper we focus our attention on the existence and multiplicity of solutions to (P).Our approach uses minimax techniques coming from critical point theory and Morse theory combined with truncation arguments.Precisely,we obtain the following result.

Theorem 1.1Assume that(f1)–(f4)hold.Then problem(P)has at least one nontrivial weak solution u0∈C10().

Furthermore, we establish the existence of at least three nontrivial weak solutions, by using an additional assumption on the reaction termf(x,t).Precisely, we have the following result.

Theorem 1.2Assume that(f1)–(f4)hold.In addition we will assume the following condition:

(f5)f(x,t)t≥0for a.a.x∈Ω, all t∈Rand the set{x∈Ω :f(x,t) = 0 for somet≠ 0}has empty interior.

Then problem(P)has at least three nontrivial weak solutions u0∈N+(N+is defined in Section2), v0∈−N+and w0∈C10().

The outline of this paper is as follows.In Section 2, we introduce the required preliminary knowledge on spaceW1,H0 (Ω) and recall some necessary concepts and results in Morse theory.In Section 3,we obtain several preliminary lemmas which are needed for the proofs of our main results.The proofs of Theorem 1.1 and Theorem 1.2 will also be presented in Section 4.

2 Preliminaries

In this section, we first recall some necessary properties on Musielak-Orlicz-Sobolev space(Ω) which will be used later, see [17, 28–31] for more details.

Denote byN(Ω) the set of all generalizedN-function (see [29, p.82]).For 1< p < qand 0 ≤a(·)∈L1(Ω), we define

It is clear thatH∈N(Ω) is locally integrable and

which is known as the (△2) (see [29, p.52]).

The Musielak-Orlicz spaceLH(Ω) is defined by

equipped with the Luxemburg norm

It is clear that the spaceLH(Ω) is a uniformly convex, and hence reflexive Banach space.The related Sobolev spaceW1,H(Ω) is defined by

with the norm

We denote by(Ω) the completion ofC∞0(Ω) inW1,H(Ω).With these norms, the spaces(Ω) andW1,H(Ω) are uniformly convex and so, reflexive Banach spaces; see [17] for the details.

Proposition 2.1(see [14, Proposition 2.1])Set ρH(u) = ∫Ω(|u|p+a(x)|u|q)dx.Foru∈LH(Ω), we have

(i)For u≠0,|u|H=λ⇔ρH()=1.

(ii) |u|H<1(=1;>1)⇔ρH(u)<1(=1;>1).

(iii)If|u|H≥1, then|u|pH≤ρH(u)≤|u|qH.

(iv)If|u|H≤1, then|u|qH≤ρH(u)≤|u|pH.

Proposition 2.2(see [17, Proposition 2.15, Proposition 2.18]) (1)If1 ≤ϑ≤p∗, thenthe embedding from W1,H0 (Ω)to Lϑ(Ω)is continuous.In particular, if ϑ∈[1,p∗), then theembeddingis compact.

(2)Assume that(1.2)holds.Then the Poincare’s inequality holds, that is, there exists a positive constant C0such that

(3)The embeddingare continuous for allϑ∈[1,p].

By the above Proposition 2.2(1), we know that there existscϑ>0 such that

where |u|ϑdenotes the usual norm inLϑ(Ω) for all 1 ≤ϑ

Remark 2.1The Poincare’s inequality has been proved also in[32]under the more general assumption

Furthermore, we observe that, sincep∗>p（1+）, both (1.2) and (2.2) implyq

In order to discuss the problem (P), we need to define a functional in(Ω):

We know that,J∈C1((Ω),R)and double phase operator −div(|∇u|p−2∇u+a(x)|∇u|q−2∇u)is the derivative operator ofJin the weak sense (see [33]).We denoteL=J′:(Ω) →((Ω))∗, then

for allu,v∈(Ω).Here ((Ω))∗denotes the dual space of(Ω) and 〈·,·〉 denotes the pairing between(Ω) and ((Ω))∗.Then, we have the following result.

Proposition 2.3(see [14, Proposition 3.1])Set E=(Ω), L is as above, then

(1)L is a continuous, bounded and strictly monotone operator.

(2)L is a mapping of type(S)+, i.e., if un⇀u in E andimplies un→u in E.

(3)L is a homeomorphism.

The Banach spaceC10() is an ordered Banach space with positive (order) cone given by

It has nonempty interior given by

Now, we introduce some elements of critical point and Morse theories needed in the sequel.LetXbe a Banach space andX∗be its topological dual.Letϕ∈C1(X,R).We setKϕ={u∈X:ϕ′(u) = 0}, Kcϕ= {u∈Kϕ:ϕ(u) =c} and, for everyc∈R, denoteϕc= {u∈X:ϕ(u)≤c}.Let (X1,X2) be a topological pair withX2⊂X1⊂X, then for every integerk≥0,we denote byHk(X1,X2) thekth-relative singular homology group with integer coefficients.Letu0∈Kcϕbe isolated.Then the critical groups ofϕatu0withϕ(u0)=care defined by

whereUis a neighborhood ofu0such thatKϕ∩ϕc∩U={u0}(see[34]).The excision property of singular homology implies that above definition is independent of the particular neighborhoodU.Assume that theϕ∈C1(X,R) satisfies the (Cc)-condition and infϕ(Kϕ)>−∞.Choosingc

see [35] for details.

Let us recall the definition of Cerami condition [36].

Definition 2.1Let X be a Banach space.ϕ∈C1(X,R)is said to satisfy condition(C)cat the level c∈R, if the following fact is true:For any sequence{uk}⊂X such that

{uk}possesses a convergent subsequence.

The following mountain pass theorem obtained by Motreanu-Motreanu-Papageorgiou [37]will be used to seek the existence of solutions.

Theorem 2.1Let X be a Banach space, ϕ∈C1(X,R), and assume that ϕ satisfies the(C)c-condition.Let u0,u1∈X, u0≠u1, satisfy‖u1−u0‖>ρ>0, and assume that

whereΓ={γ∈C([0,1],X):γ(0)=u0,γ(1)=u1}.

Then c≥mρand c is a critical value of ϕ, that is, there exists∈X such that ϕ′(u)= 0and ϕ(u)=c.

3 Some Preliminary Lemmas

In this section, we give some preliminary lemmas which are crucial for proving our results.Firstly, we show that Cerami condition holds.

Lemma 3.1If assumption(f2)−(f4)hold,then the functional ϕ satisfies the(C)c-condition for each c>0.

ProofLet {un}⊂(Ω) be a (C)csequence, that is,

wherecn→0 asn→+∞.

First of all, we claim that the sequence {un} is bounded in(Ω).Indeed, arguing by contradiction, we suppose that ‖un‖→+∞asn→+∞.Define, for anyn∈N.It is clear that {vn}⊂Eand ‖vn‖=1 for anyn∈N.Thus, going if necessary to a subsequence,we may assume that

Set Ω≠:={x∈Ω:v(x)≠0}.Ifx∈Ω≠, then it follows from (3.2) that

which yields

By the hypothesis (f3), it follows that for eachx∈Ω≠we have

Also by virtue of hypothesis (f3), we can findt0>0 such that

Moreover from hypothesis (f2), we have that there exists a positive constantC1such that

Then, by (3.4)–(3.5), there is a constantC2∈R such that

which implies that

that is,

Recalling ‖un‖>1 fornlarge, using (3.1) we have

which shows that

Similarly, from (3.1), we deduce that that

This combined with (3.8) yields

fornlarge enough.

Next, we claim that |Ω≠| = 0.In fact, if |Ω≠| ≠ 0, then from (3.3), (3.7), (3.9) and the Fatou’s lemma, we obtain that

Therefore, by (3.8) and (3.10), we conclude

which is a contradiction.Therefore, |Ω≠|=0 andv(x)=0 a.e.in Ω.

Sinceϕ(tun) is continuous int∈[0,1], for eachnthere existstn∈[0,1],n=1,2,···, such that

It is clear thattn>0 andϕ(tnun) ≥c >0 =ϕ(0) =ϕ(0·un).Iftn<1, then by usingwe deduce that

Iftn=1, then it follows from (3.1) that

Hence, from (3.12)–(3.13), we obtain

On one hand, by (f4), (3.1) and (3.11), for anyt∈[0,1], we achieve that

Let {Rk}k∈Nbe a positive sequence of real numbers such thatRk>1 for anykandRk→+∞ask→+∞.Then

Moreover,due to the fact thatvn→0 inLr(Ω) andvn(x)→0 a.e.x∈Ω asn→+∞, by (f1)and the Lebesgue dominated convergence theorem, we have that for fixedk∈Nthat

Recall that ‖un‖→+∞asn→+∞.So, we have either ‖un‖>Rkorfornlarge enough.Consequently, by (3.11) and (3.16), we deduce for fixk∈Nthat

for anynlarge enough.From (3.17), lettingn,k→+∞we have

From (3.15) and (3.18) we obtain a contradiction.Therefore we infer that the sequence {un}is bounded in(Ω).

Finally, we turn to proving that any (C)csequence has a convergent subsequence.Indeed,by the boundedness of {un}, passing to a subsequence if necessary, still denoted by {un}, we may assume that

Using Proposition 2.2(1), we have

It is easy to compute directly that

Note that

Moreover,by (3.1), it is easy to see that

Therefore, the combination of (3.19)–(3.21) implies

Therefore, it follows thatun→u0inW1,H0(Ω) becauseLis a mapping of type (S)+(see Proposition 2.3).This ends the proof of lemma.

Our second result is the following lemma.

Lemma 3.2Assume that(f1)–(f3)hold.Then the following assertions hold:

(a)there exist ρ>0and δ >0such that ϕ(u)≥δ for each u∈(Ω)with‖u‖=ρ;

(b)there exists v∈(Ω)such that ϕ(v)<0and‖v‖>ρ.

ProofVerification of (a).Since 10 such that

Using assumptions (f1) and (f2), we deduce that for anyε>0, there is aCε>0 such that

for all (x,t)∈Ω×R, wherer∈[1,p∗) was given in (f2).

Thus, foru∈(Ω) with ‖u‖<1 sufficiently small.By (3.24) and Proposition 2.2(2),

and so there existρ>0 andδ >0 such thatϕ(u)≥δfor anyu∈(Ω) with ‖u‖=ρ.

Verification of (b).By the assumption (f3), for anyM >0, there exists a constantδM>0 such that

for |t|>δMand for almost allx∈Ω.Also, by (f2), for allx∈Ω and |t|≤δM, we have

The above two inequalities imply that there exists a constantCM>0 such that

Takeφ∈W1,H0 (Ω) withφ>0 on Ω andt>1.Then, the relation (3.26) implies that

IfMis large enough that

This means that

Hence, there existsv=t0φ∈(Ω) such thatϕ(v)<0 and ‖u‖>ρ.

Next we compute the critical groups of the energy functionalϕat infinity.

Lemma 3.3Assume that(f1)−(f4)hold.Then Ck(ϕ,∞)=0for all k≥0.

ProofLet∂B1= {u∈(Ω) : ‖u‖ = 1}.From (f1) and (f2), for anyM >0, there existsCM>0, such that

Thus, for anyu∈∂B1andt>1, we get

By the arbitrariness ofM, we have

Moreover,foru∈∂B1andt>1, by (f4), one yields

We extendt(·) on(Ω){0} by

for allu∈(Ω){0}.It is clear thatt0∈(Ω){0}andϕ(t0(u)u)=ρ0.Therefore, we have

Denoting by

for allλ∈[0,1] and allu∈(Ω).

The above facts imply that

Next, we consider the radial retractionr:(Ω){0}→∂B1defined by

On one hand, using this deformation we deduce that

On the other hand, using radial retractionr(·), we see that

Hence, by (3.30)–(3.31)and [38, Theorem 6.5], we conclude that

Again from(3.29)and (3.32), we conclude thatϕρ0and∂B1are homotopy equivalent.In view of [37, Proposition 6.11]

Invoking Problems (4.154), (4.159) of Gasinski-Papageorgiou [39], we infer that∂B1is contractible.Again from [37, P.147], we haveHk((Ω),∂B1) = 0 for allk≥0.This,together with (3.33), showsHk((Ω),ϕρ0)=0 for allk≥0.As usual we assume thatKϕis finite (or otherwise we already have an infinity of nontrivial solutions).Hence, if we chooseρ0such thatqρ0−∫Ω F(x,u)dx+|g|1<0, then we haveCk(ϕ,∞) =Hk((Ω),ϕρ0) = 0 for allk≥0.

4 The Proof of Main Theorems

Proof of Theorem 1.1LetX=(Ω) andu0= 0.We know thatϕsatisfies the(C)c-condition from Lemma 3.1 andϕ(0) = 0.In view of Lemma 3.2(b), we get trivially thatu= 0 is a local minimizer ofϕ.Thus, it follows from Lemmas 3.1–3.2 that all conditions of Theorem 2.1 are satisfied.Hence, problem (P) has at least one nontrivial weak solutionu0.Again using [40, Lemma 4.1], the solutionu0is inC10().Then the proof is completed.

Now, we are ready to prove Theorem 1.2.

Proof of Theorem 1.2Firstly, we consider the functionsF±:Ω×R →R given as

and the functionalsϕ±:(Ω)→R given as

Due to hypotheses (f1)−(f4), we deduce thatϕ±∈C1((Ω),R) and

for allv∈(Ω).

Claim 1The functionalϕ+satisfies the (Cc)-condition if and only if it satisfies the (Cc)-condition with respect to all the sequences {un}⊂(Ω) such thatun(x)≥0 for allx∈Ωand alln∈N.

In fact, if {un} ⊂(Ω) and (1+‖un‖)ϕ+(un) →0 asn→+∞.Then, there exists a sequence {εn} of nonnegative real numbers such thatεn→0 asn→+∞and

Moreover,by (f5), one yields

Takevn=min{0,un}.Then, the relation (4.1) and Proposition 2.1 imply that

This shows ‖vn‖→0 asn→+∞.The proof of Claim is complete.

Now, for allu∈(Ω)such thatu(x)≥0for allx∈Ω, one easily deduces

Therefore, by Lemma 3.1, we deduce that the functionalϕ+satisfies the (Cc)-condition for all the sequences {un} ⊂(Ω) such thatun(x) ≥0 for allx∈Ω, alln∈N.Clearly,Lemma 3.2 also holds for the functionalϕ+.The above facts (by Theorem 2.1) imply that there exists a functionu0∈(Ω) such that

for allv∈(Ω).

Choosingv=min{0,u0}, we get thatv=0, becausef(x,u+0(x))v(x) =0 for a.a.x∈Ω.It is obviously thatu0(x)≥0 for allx∈Ω.Thus,f(x,u+0(x))=f(x,u0(x)) for allx∈Ω.Hence,

for allv∈(Ω).This shows thatu0is a nonnegative nontrivial weak solution of problem(P).By again using [40, Lemma 3.5], we deduce thatu0∈N+.

Claim 2Ck(ϕ+,u0)=δk,1Z for allk≥0, whereδk,m=1 ifk=mandδk,m=0 ifk≠m.

Without loss of generality, we may assume thatKϕ+={0,u0}.Recall thatu=0 is a local minimizer ofϕ+andu0is a critical point ofϕ+of mountain pass type.So,by the similar proof of Lemma 3.2(1), we can show that there existsδ >0 such that

Letν−<0< ν+< δand consider the inclusionsConsider the following corresponding long exact sequence of singular homology groups (see [38, p.143]):

wherei♯,j♯are induced by inclusions.It follows thati♯andi♯are isomorphisms.Thus, due to the fact thatKϕ+={0,u0} andν−<0=ϕ+(0), by using Lemma 3.3, we deduce that

Moreover,it follows from 0=ϕ+(0)<ν+that

Similarly, we also deduce that

As a consequence of (4.4)–(4.6) and taking into account (4.3), we infer that only the tail of that chain (i.e.,k=1) is nontrivial.Consequently, by using the rank theorem, (4.3)–(4.4) and(4.6), we obtain that

Using the fact thatu0is a critical point ofϕ+of mountain pass type, we get that

Finally, due to the fact that only fork=1 the chain (4.3) is nontrivial and using again (4.5)–(4.8), we observe that

Claim 3Ck(ϕ,u0)=Ck(ϕ+,u0) for allk≥0.

First of all, we introduce the homotopy functionh:[0,1]×(Ω)→R defined as

Assume that there exist {λn}⊂[0,1] and {un}⊂(Ω) such that

which yields that

for allv∈(Ω).Thenunis a weak solution to

where we have setfn(x,t)=f(x,t+)+(1 −λn)f(x,−t−).

By the assumption (f1), for anyε>0, there exists a constantδε∈(0,1) such that

for |t|≤δεand for almost allx∈Ω.Also, by (f2), for allx∈Ω and |t|≥δε, we have

The above two inequalities imply that there exists a constantCε>0 such that

Thenun∈L∞(Ω) (see [17, Sec.3.2]) withL∞-bounded independent ofn.This implies that there exists a constantd>0, such that

Lethn(x) :=f(x,u+n(x))+(1 −λn)f(x,−u−n(x)), n∈N,x∈Ω.Then from (4.10)–(4.11), we get

Again from Lemma 3.3 of Fukagai-Narukawa[40,p.545],we conclude that there existα∈(0,1)andM >0 such that

Using the compactness of the embeddingtogether with (4.9), it follows thatun→u0inC1().

Recall thatu0∈N+(see Claim 1).Therefore,un∈N+forn≥1 large, which implies that there exists an0∈Nsuch thatun∈N+for alln≥n0.Then {un:n≥n0} are distinct positive solutions of (P), which leads to contradiction asKϕ+must be finite.Consequently,(4.9) can not happen and hence we obtain thatCk(ϕ,u0) =Ck(ϕ+,u0) for allk≥0 (it is a direct consequence of the homotopy invariance of critical groups, see [41, Theorem 5.2]).This proves Claim 3.

By reasoning in a similar way as above, Lemma 3.2 also holds for the functionalϕ−.Thus,there is another functionv0∈(Ω)that is a nonpositive nontrivial weak solution of problem(P).Similar to the proof of Claims 1–3, we can obtain that

Hence, we retrieve the two constant sign solutionsu0∈N+andv0∈−N+.If we assumeKϕ= {0,u0,v0} which means thatu0andv0are the only nontrivial solutions of (P), then by Claim 2 we have

Moreover,we recall thatu=0 is local minimizer ofϕ.So that

Then from (4.12)–(4.13), Lemma 3.3 and the Morse relation, we may write

whereβk∈N.Assume that 0,u0andv0are the only critical points ofϕ.Then the Morse inequality becomes 2(−1)1+(−1)0+(−1)k=(−1)k.This is impossible.Thusϕmust have at least one more critical pointw0.So (P) has at least third nontrivial solution.This completes the proof of Theorem 1.1.

AcknowledgementThe authors would like to thank the anonymous reviewers for their careful reading and valuable comments.