Digital Cofibration and Digital Lusternik-Schnirelmann Category in the Sense of Subdivision∗

Hongjie ZHANGLinan ZHONGHao ZHAO

Abstract In this paper, using the notion of subdivision, the authors generalize the definition of cofibration in digital topology and show that this kind of cofibration is injective in the sense of subdivision.Meanwhile, they give the necessary condition under which a digital map is a cofibration.Furthermore, they consider the Lusternik-Schnirelmann category of digital maps in the sense of subdivision and give several fundamental homotopy properties about it.

Keywords Digital topology, Digital cofibration, Lusternik-Schnirelmann category

1 Introduction

In digital topology, the basic object is a digital image.A digital image is a finite set of integer lattice points in an ambient Euclidean space with an adjacency relation between points.In our daily life, the sets which can be handled on computers are discrete sets or finite sets.Studying digital topology is helpful to develop artificial intelligence,image recognition and some others technology.Many topologists have made some progress along this direction.In [3, 5],some basic concepts of digital topology were introduced and some results of digital topology via techniques from classical topology were obtained.In [3], Boxer constructed the digital fundamental group of a digital image based on the notions of digitally continuous functions and digital homotopy.In [5], it was shown that a digital imageX⊆Zn(n≥3) admits a continuous analogC(X) ⊆Rnsuch that the digital fundamental group ofXis isomorphic to that ofC(X).However, the definition of digital fundamental group in [3, 5] can not greatly resemble the classical construction of the fundamental group of a topological space.

In [4], Ege-Karaca gave the definition of fibration in digital topology with analogy of the definition of fibration in classical algebraic topology and showed that the composition or the product of fibrations is still fibration.However, the defined digital fibrations in [4] do not coincide with classical fibrations in topology in aspect of some basic properties.In[1–2],Borat-Vergili defined the notion of Lusternik-Schnirelmann category(LS category for short)of a digital space and a digital map, respectively.In [1], it was shown that the digital LS category of a digital space is a digital homotopy invariant.In [2], Borat-Vergili showed how the digital LS category of a digital map behaves after changing the adjacency relation.

According to the above statements, we see that the former literatures just simply directly translate the topological notions into the digital topology.This leads to no more results can be obtained as the classical topology.Considering this shortcoming, in [7], Lupton-Oprea-Scoville introduced the idea of subdivision and redefined some concepts of digital topology such as cofibrations and LS category.By using this new notion of digital cofibrations, they established some basic examples such as the inclusion of one or both endpoints into an interval being a cofibration.In [6], Lupton-Oprea-Scoville redefined the fundamental group for digital images and showed that this kind of fundamental group can be preserved in the sense of subdivision.In [8] Lupton-Oprea-Scoville mainly discussed the subdivision of digital maps and established some related results about the subdivision of digital maps with one or two dimensional domains.

We note that Lupton-Oprea-Scoville [7] only gave the definition of digital cofibrations as inclusion maps without considering the injective map.Hence by virtue of the notion of subdivision, we define a generalized digital cofibration and show that the generalized cofibration is injective in the sense of subdivision.Meanwhile, we define LS category of a digital map in the sense of subdivision and give some basic properties of this notion under some restricted conditions.Our main results are stated as follows.

Theorem 1.1If a digital map f:A→X is a digital cofibration, then f is injective in the sense of subdivision.

Theorem 1.2For a given digital map f:X→Y, suppose that the subdivision S(f,k)exists for any k≥0.Then

(1)for any digital map g:Y→Z, there isDcat(g◦f)≤min{Dcat(f),Dcat(g)},

(2)for any digital map f′:X′→Y′, there isDcat(f×f′)≤Dcat(f)·Dcat(f′),whereDcat(f)denotes the digital LS category of the digital map f.

This paper is organized as follows.In Section 2, we introduce some notions in the sense of subdivision defined in [7] and recall some basic properties about these notions.In Section 3,we give the proof of Theorem 1.1 and give a condition under which a digital map is a digital cofibration.In Section 4, we define the notion of digital LS category of a digital map and then give the proof of Theorem 1.2.

2 Some Preliminaries on Digital Topology

In this section, we introduce some basic notions in digital topology.

Definition 2.1(see [7])A digital image X is a finite subset X⊆Znwith a particular adjacency relation inherited from that ofZn.Two points x= (x1,···,xn) ∈X⊆Znand y= (y1,···,yn) ∈X⊆Znare adjacent if their coordinates satisfy|xi−yi| ≤1for each i=1,···,n, denoted by x∼Xy.

Definition 2.2(see [7])For digital images X⊆Znand Y⊆Zm, a function f:X→Y is called continuous if f(x)∼Yf(y)whenever x∼Xy.By a map of digital images, we mean a continuous function.

Definition 2.3(see[7])An isomorphism between two digital images is a continuous bijection f:X→Y which admits a continuous inverse g:Y→X.

Iff:X→Yis an isomorphism, thenXis isomorphic toY, being denoted byXY.

Definition 2.4(see [7])A digital interval of length N is the set{0,1,···,N}, denoted by IN.

Definition 2.5(see [7])The product of digital images X with Y is the Cartesian product of sets X×Y with the adjacency relation(x,y)∼X×Y(x′,y′)when x∼Xx′and y∼Yy′.

Definition 2.6(see [7])Given maps of digital images fi:Xi→Yi(i= 1,2), we define their product in the usual way as

by(f1×f2)(x1,x2)=(f1(x1),f2(x2)).

The product of maps is obviously a continuous map.

Definition 2.7(see [7])For a given digital image X∈Znand each k≥2, a k-fold subdivision of X, denoted by S(X,k), is defined by

where

for any x=(x1,···,xn)∈X.A projection ρk:S(X,k)→X is defined byfor any y=(y1,···,yn)∈S(X,k).

Proposition 2.1(see [7])For any digital images X,Y⊆Zmand any k≥2, there is

and the standard projection ρk:S(X×Y,k)→X×Y can be indentified with

Proposition 2.2(see[7])For any k,l∈Zand digital image X⊆Zn,there is S(S(X,k),l)S(X,kl).

Definition 2.8(see [7])Let f,g:X→Y be two digital maps.We say that f and g are homotopic, denoted by f≃g, if for some N≥1, there is a map

such that H(x,0)=f(x),H(x,N)=g(x)for any x∈Y.In this case, H is called a homotopy from f to g.

Proposition 2.3(see [7])Homotopy relation is an equivalence relation on the set of all maps from X to Y.

Proposition 2.4(see [7])For digital maps g,h:X→Y and f:Y→Z, if g≃h, then f◦g≃f◦h.

Definition 2.9(see [7])A digital image X is called contractible if there are some x0∈X and some N such that we have a homotopy H:X×IN→X satisfying H(x,0) =x and H(x,N)=x0.

Definition 2.10A digital map f:X→Y is called null homotopic if there are some y0∈Y and some N such that we have a homotopy H:X×IN→Y satisfying H(x,0) =f(x)with H(x,N)=y0.

Definition 2.11(see [6])A digital image X is called subdivision-contractible if for some subdivision S(X,k)of X,some x0∈X and some N,there is a homotopy H:S(X,k)×IN→X such that H(x,0)=ρk(x)and H(x,N)=x0for any x∈X.

Definition 2.12For two digital images X,Y⊆Zn.Two digital maps f:S(X,k) →Y and f:S(X,l)→Y are called subdivision-homotopic if for some k′,l′with kk′=ll′=m, such that we have a homotopy f◦ρk′≃g◦ρl′.In particular, if g is a constant map, then f is called subdivision-null-homotopic.

Definition 2.13(see [7])By an inclusion of digital images i:A→X⊆Znwe mean that A is a subset of X.

It is obvious that given an inclusion of digital images of the same dimensioni:A→X⊆Zn, we have an obvious corresponding continuous inclusion of subdivisionsS(i,k):S(A,k) →S(X,k) such that the following commutative diagram holds:

In this case, We say that the mapS(i,k) covers the mapi.For anya=(a1,···,an)∈Aandt=(t1,···,tn) (0 ≤t1,···,tn≤k−1)∈(Ik−1)n, the pointsS(a,k)⊆S(A,k) can be written as

withρk(ka+t)=afor allt∈(Ik−1)n.ThusS(i,k):S(A,k)→S(X,k) can be written as

wherei(a)=(a1,···,an)∈X.

Remark 2.1For two inclusion of digital imagesi:A→Xandj:B→A, we obviously haveS(i◦j,k)=S(i,k)◦S(j,k).

Remark 2.2It is known from [7] that a general mapf:X→Ymay not induce a subdivision mapS(f,k):S(X,k)→S(Y,k) which makes the following diagram

commute.In [8], Lupton-Oprea-Scoville gave a full discussion onS(f,k).

3 Digital Cofibrations

In classical topology, a cofibrationi:A→Xis a map satisfying the homotopy extension property.A mapi:A→Xis a cofibration if for any maps

and

satisfyingH(a,0)=f◦i(a), there is a map

such that the diagram

commutes.The inclusioni: {0}→Iis a classical cofibration in classical toplogy.

As we know, cofibration as well as fibration are two fundamental notions in homotopy theory of various categories.They are the starting point of research on homotopy theory.The cofibraiton may help us to understand the notion of homology via the cofibre sequence.Thus in order to construct the system of digital homotopy theory, it is meaningful for us to understand the digital cofibration in digital topology.In [7], it was shown that it is difficult to repeat this definition in the digital setting due to the fact that the inclusioni: {0} →IMfails to be a cofibration.In order to make the inclusioni: {0} →IMbe a digital cofibration,Lupton-Oprea-Scoville[7] redefined the digital cofibration in mapping space in a less rigid way.In what follows, we give another definition of digital cofibration which is equivalent to that in[7] in a dual way.In the category of topological spaces, Spanier [9] gave a general definition of cofibration which needs not to be an inclusion.Inspired by the above definition of the digital cofibration, we also give a general definition of digital cofibration as follows.

Definition 3.1A digital map f:A→X⊆Znis a cofibration if for a given commutative diagram

there are subdivisions S(X,k)and S(IN,l)as well as maps S(f,k):S(A,k) →S(X,k)and:S(X,k)×S(IN,l)→Y such the following commutative diagram holds:

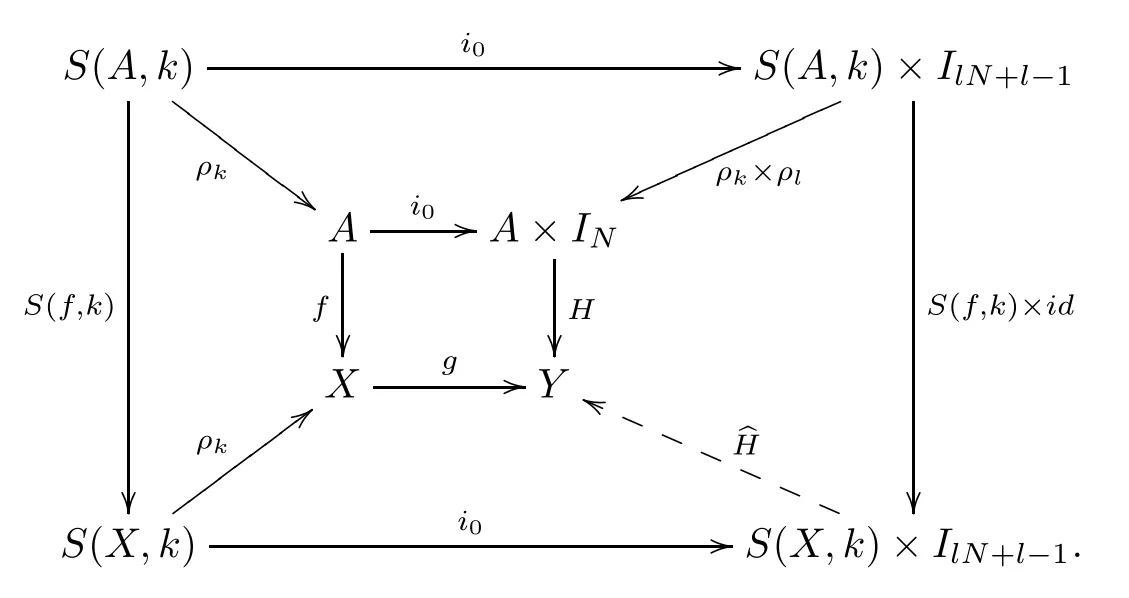
Remark 3.1Definition 3.1 is equivalent to the one in [7] in the special case of inclusion of digital images.

It is known that a cofibration is injective in the category of topological spaces[9].In digital topology, we also have an analogous result in the digital category as follows.

Theorem 3.1(see Theorem 1.1)If a digital map f:A→X is a digital cofibration, then f is injective in the sense of subdivision.

ProofLetCNA=A×IN/A×{0}.We have a commutative diagram

whereH(a,0) = ∗,H(a,t) = [(a,t)].Sincefis a digital cofibration, there are subdivisionsS(X,k),S(IN,l), and mapsS(f,k):S(A,k) →S(X,k) and:S(X,k)×S(IN,l) →CNAsuch that the following commutative diagram holds:

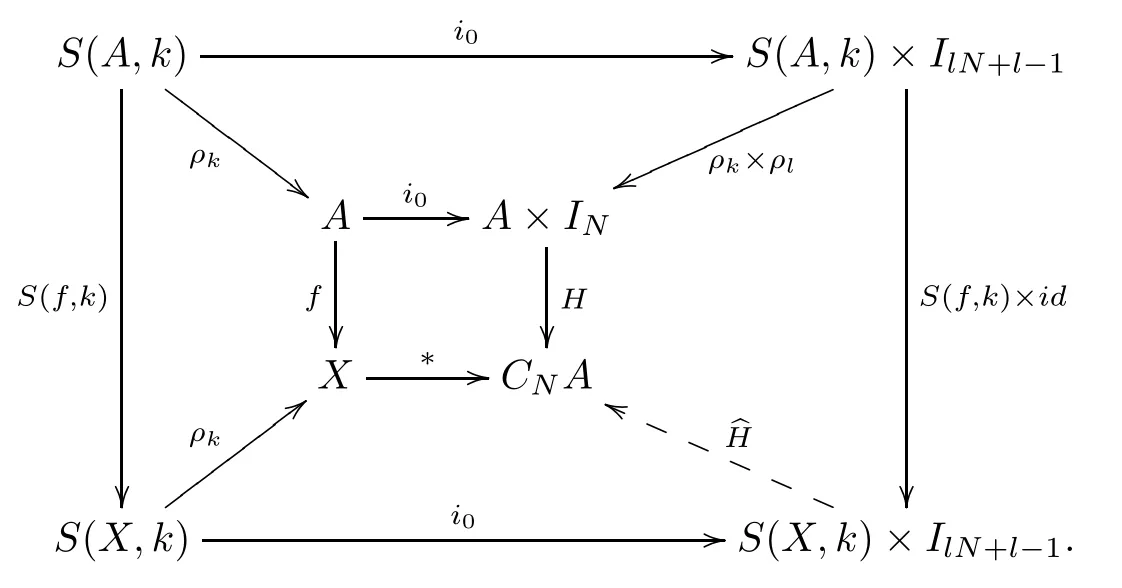
For anya∈S(A,k), we have

which impliesS(f,k)(a1)≠S(f,k)(a2) wheneverρk(a1)≠ρk(a2).

Moreover, ifρk(a1) ≠ρk(a2) andρk(S(f,k)(a1)) ≠ρk(S(f,k)(a2)), then it means thatS(f,k)(a1) andS(f,k)(a2) do not belong to the sameS(x,k) (x∈X).Thus we have

which follows thatfis injective.

In [8], it is shown that ifA⊆Znandkis odd, a digital mapf:A→Xcan always induce a mapS(f,k):S(A,k) →S(X,k) satisfyingρk(S(f,k)(a1)) ≠ρk(S(f,k)(a2)) whenρk(a1)≠ρk(a2).

Lemma 3.1For any digital map f:A→X, if we have a diagram

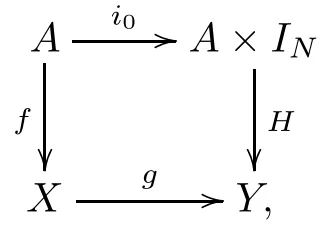
then for any subdivision S(IN,l) (l≥2), there is a digital map φ:A×S(IN,l)∪X×{0}→Y such that the following commutative diagram holds:

=A×S(IN,l)∪X×{0}/with the relation(a,0)(x,0)if and only if f(a)=x.

ProofFor anyx∈S(X,k),a∈S(A,k) andt∈S(IN,l), define

In order to show thatφis continuous, we just need to show that [(a,1)]∼[x,0](a∈A,x∈X)impliesφ([a,1])∼φ([x,0]).This directly follows from

In[7],Lupton-Oprea-Scoville gave a digital version of the necessary condition for an inclusion of digital images being a cofibration.Similarly, under the condition that the subdivision mapS(f,k) exists, we give a digital version of the necessary condition for a general digital map being a cofibration.

Theorem 3.2(1)If a digital map f:A→X is a digital cofibration, then for any IN, there are subdivisions S(X,k), S(IN,l), and a map

for some m∈Nsuch that

for any a∈S(A,k).

(2)A digital map f:A→X is a digital cofibration if for any k∈Nand IN, there are a map S(f,k):S(A,k)→S(X,k)satisfying

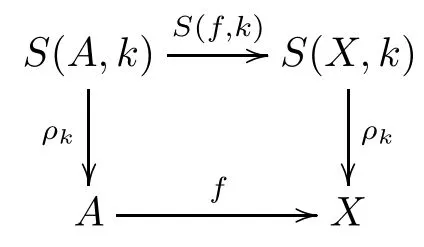
and a map R:S(X,k)×S(IN,lm)→X such that

for any a∈S(A,k).

Proof(1)We define the digital mapsg:X→byg(x)=[x,0]andH:A×S(IN,l)→byH(a,t)=[a,t], respectively.It follows the commutative diagram

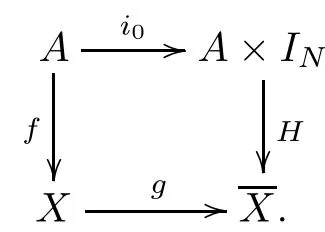
Sincef:A→Xis a digital cofibration, there are subdivisionsS(X,k) andS(IN,lm), with mapsS(f,k):S(A,k) →S(X,k) and:S(X,k)×S(IN,lm) →Ysuch that the following diagram holds:

LetR=.Thus we have

R(x,0)=g◦ρk(x)=[ρk(x),0], R(S(f,k)(a),t)=H(ρk(a),ρm(t))=[ρk(a),ρm(t)].

(2) Suppose that there are two digital mapsg:X→YandH:A×IN→Ysuch that the following commutative diagram holds:

We define a mapR:S(X,k)×S(IN,lm)→Xby

According to Lemma 3.1, there is a digital mapφ:A×S(IN,l)∪X×{0}→Ysuch that the following commutative diagram holds:

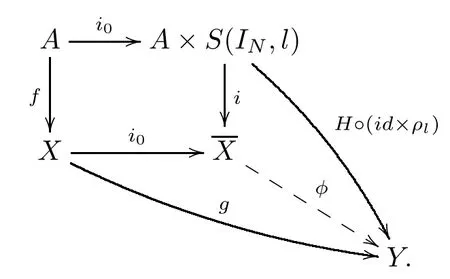
Hence,for two digital mapsg:X→YandH:A×IN→Ysatisfying the commutative diagram

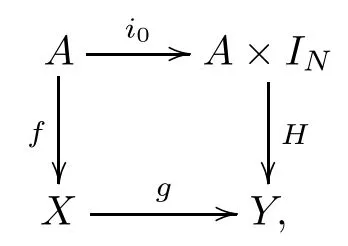
we have the following commutative diagram

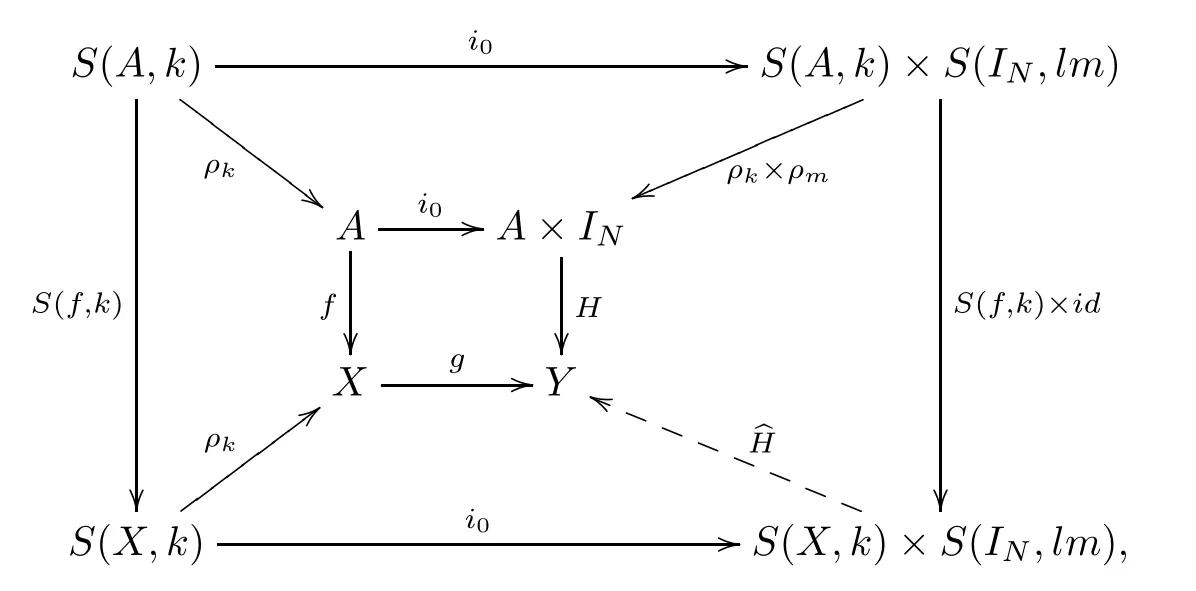
which shows thatf:A→Xis a digital cofibration.

By applying the above results, we can give an example of injective map which is a digital cofibration but not an inclusion.

Example 3.1For the digital imagesX= {(0,2,1),(0,1,0),(1,1,0),(2,1,0),(2,0,1)}andY=I2×I2, we define a digital mapf:X→Ybyf(0,2,1) = (0,2),f(0,1,0) = (0,1),f(1,1,0) = (1,1),f(2,1,0) = (2,1),f(2,0,1) = (2,0).It is easy to check thatfis injective.We define a digital functionD:S(Y,2)→S(f(X),2) by

and a digital functionD′:S(Y,2)×S(I1,2)→S(f(X),2)×S(I1,2)∪S(Y,2)×{0} by

It is routine to check thatDandD′are not continuous but (ρ2×ρ2)◦D′is continuous.Also we have a digital mapS(f,2):S(X,2)→S(Y,2) defined by

which makes the following diagram commutes:

Furthermore, we have an obvious isomorphic digital map

LetR=g◦((ρ2×ρ2)◦D′):S(Y,2)×S(I1,2)→X×I1∪Y×{0}/.Thus we have

It follows thatf:X→Yis a digital cofibration according to Theorem 3.2(2).

4 Lusternik-Schnirelmann Category of Digital Map

In [7], Lupton-Oprea-Scoville redefined the LS category in digital topology via the notion of subdivision.Inspired by the new definition in [7], in this section we give a definition of LS category for the digital map via the notion of subdivision and give some fundamental properties about this notion.

Definition 4.1(see [7])Let i:A→X be an inclusion and we say A is categorical in X if there are x0∈X, INand a map H:A×IN→X such that H(a,0)=i(a), H(a,N)=x0for any a∈A.

Definition 4.2(see [7])Let i:A→X be an inclusion.We say that A is subdivisioncategorical in X if there are subdivision S(X,k), x0∈X, INand a map H:S(A,k)×IN→X such that H(a′,0)=i◦ρk(a′), H(a′,N)=x0for any a′∈S(A,k).

Definition 4.3(see [7])The digital category of X, denoted byDcat(X), is the smallest number n≥0for which there is a covering of X by n+1subsets that are subdivision-categorical in X.

Definition 4.4The digital category of a digital map f:X→Y, denoted byDcat(f), is the smallest number n≥0for which there is a covering of X by n+1subsets{A1,···,An+1}that each f(Aj) (j= 1,···,n)is subdivision-contractible in Y, i.e., there are kjand N, with the map Hj:S(Aj,kj)×IN→Y such that Hj(a′,0) =f|Aj◦ρkj(a′)and Hj(a′,N) =yjfor any a′∈S(Aj,kj).

Remark 4.1When we takef=idX:X→X, then there is Dcat(X)=Dcat(idX).

In what follows, we assume that for any digital map and anyk≥0, there is a subdivision mapS(f,k):S(X,k)→S(Y,k) such that the following commutative diagram holds:

Proposition 4.1If f:X→Y is a digital map, thenDcat(f)≤min{Dcat(X),Dcat(Y)}.

ProofAssume that Dcat(X) =nand {A1,···,An+1} is a subdivision-contractible covering onX.For every inclusionij:Aj→X, there is a subdivisionS(Aj,kj), and a mapHj:S(Aj,kj)×IN→Xsuch that

LetFj=f◦Hj:S(Aj,kj)×IN→Y.It is routine to check thatf(Aj) (j= 1,···,n) are subdivision-contractible inYand thus we have Dcat(f)≤Dcat(X).

Assume that Dcat(Y)=mand {V1,···,Vm+1} is a subdivision-contractible covering onYwhich implies that {f−1(V1),···,f−1(Vm+1)} is a covering onX.For every inclusioni′l:Vl→Y, there is a subdivisionS(Vl,k′l) and a mapGl:S(Vl,k′l)×IM→Ysuch that

For the mapf:X→Y, there is a subdivisionS(f,k′l):S(X,k′l) →S(Y,k′l) such that the following commutative diagram holds:

DefineG′l:S(f−1(Vl),k′l)×IN→YbyG′l(x,t)=Gl(S(f,k′l)|S(f−1(Vl),k′l)(x),t).Then we have

which implies Dcat(f)≤Dcat(Y).Thus we have Dcat(f)≤min{Dcat(X),Dcat(Y)}.

Proposition 4.2If f≃g:X→Y, then there isDcat(f)=Dcat(g).

ProofWe just need to show that Dcat(f) ≤Dcat(g).Assume that Dcat(f) =nand{A1,···,An+1} is a covering ofXwithf(Aj) (1 ≤j≤n+1) being subdivision-contractible inY.Then there is a subdivisionS(Aj,kj) and a mapHj:S(Aj,kj)×IN→Ysuch thatHj(a′,N)=yjfor someyj∈YandHj(a′,0)=f|Aj◦ρkj(a′) for anya′∈S(Aj,kj).

We defineej:S(Aj,kj) →Ybyej(a′) =yjfor anya′∈S(Aj,kj).It followsf|Aj◦ρkj≃ej.Sincef≃g, we havef|Aj≃g|Ajandf|Aj◦ρkj≃g|Aj◦ρkj.Thusg|Aj◦ρkj≃ejandg(Aj) (1 ≤j≤n) is subdivision-contractible inY.It follows Dcat(f)≤Dcat(g).

In what follows we give the proof of Theorem 1.2.

Proof of Theorem 1.2(1) Assume that Dcat(f) =n, {A1,···,An+1} is a covering onXwithf(Aj) (1 ≤j≤n+1) being subdivision-contractible inY.Then there is a subdivisionS(Aj,kj) and a mapHj:S(Aj,kj)×IN→Ysuch that

Hj(a′,0)=yjfor someyj∈YandHj(a′,N)=f|Aj◦ρkj(a′) for alla′∈S(Aj,kj).

LetH′j=g◦Hj:S(Aj,kj)×IN→Z.Then we have

It follows Dcat(g◦f)≤n=Dcat(f).

Assume Dcat(g)=m, {V1,···,Vm+1} is a covering ofYwithg(Vl) (1 ≤j≤m+1) being subdivision-contractible inZ.Then there is a subdivisionS(Vl,k′l) and a mapGl:S(Vl,k′l)×IM→Zsuch that

Gl(v′,0)=zlfor somezl∈ZandGl(v′,N)=g|Vl◦ρk′l(v′) for allv′∈S(Vj,k′l).Forf:X→Y, there is a subdivisionS(f,k′l):S(X,k′l) →S(Y,k′l) such that the following commutative diagram holds:

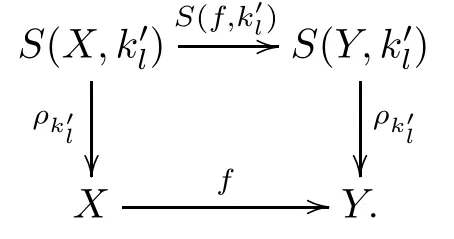
We defineG′l:S(f−1(Vl),kl)×IM→Zby

for anyx∈S(f−1(Vl),k′l) andt∈IM.Then we haveG′l(x,0)=zland

It follows Dcat(g◦f)≤m=Dcat(g) and thus Dcat(g◦f)≤min{Dcat(f),Dcat(g)}.

(2) Assume that Dcat(f) =nand {A1,···,An+1} is a covering ofXwithf(Aj) (1 ≤j≤n+1) being subdivision-contractible inY.Then there is a subdivisionS(Aj,kj) and a mapHj:S(Aj,kj)×IN→Ysuch that

for anya′∈S(Aj,kj).Assume that Dcat(f′) =mand {B1,···,Bm+1} is a covering ofX′withg(Bi) (1 ≤i≤m+1) being subdivision-contractible inY′.Then there are a subdivisionS(Bi,li) and a mapGi:S(Bi,li)×IM→Y2such that

for anyb′∈S(Bi,li).For eachAj×Bi, we letK=max{N,M} and define

Thus we can define a mapFji :S(Aj×Bi,kjli)×IK→Y×Y′by

It follow sFij((a′,b′),0)=(ykj,yli) and

which implies that (f×f′)(Aj×Bi) is subdivision-contractible inY×Y′.Since the set{Aj×Bi} (1 ≤j≤n+1,1 ≤i≤m+1) is a covering ofX×X′, then we have

AcknowledgementThe authors would like to give their thanks to the referee for his/her many helpful suggestions on the original version of this paper.