尺度无关高阶WCNS 格式1)
2023-02-25张子轩董义道黄梓全孔令发刘伟
张子轩 董义道 黄梓全 孔令发 刘伟
(国防科技大学空天科学学院,长沙 410073)
引言
计算流体力学在航空航天等诸多领域逐渐发挥越来越重要的作用[1-2],为更加真实准确地刻画复杂的流动细节,实现流动的高保真模拟,高精度数值方法应运而生.相比于高精度有限体积格式,在结构网格上,满足自由流保持特性的高精度有限差分格式的优势更加明显[3].光滑流场的数值模拟,通常使用线性格式,如紧致格式[4]等.然而,当计算包含激波时,需采用激波装配法或激波捕捉法.由于激波装配法目前还仅适用于简单构型,难以推广到包含复杂激波结构的流场的计算[5],故目前主流的求解激波的方法仍然是激波捕捉法.
Harten[6]提出的总变差不增(total variation diminishing,TVD)格式是高分辨率的激波捕捉格式之一.随后Van Leer 基于TVD 格式构造了二阶MUSCL(monotonic upstream schemes for conservation laws)格式,以减少数值耗散色散误差[7-8].然而,TVD 格式在计算复杂流动问题,如湍流时,极值点附近存在降阶现象.为在不降阶的前提下提高精度,高阶格式得以发展.高阶格式可以在一定程度上减少耗散和色散误差[9],并且在相同精度的条件下较低阶格式更为高效[4].此外,相较于低阶格式,高阶格式具有更好的并行可扩展性[10].
作为对高阶基本无振荡ENO(essentially nonoscillatory)格式[11-12]的改进,Liu 等[13]提出的加权基本无震荡WENO 格式是目前较为理想的高阶激波捕捉格式之一.WENO 格式较好地兼顾了间断区域的数值震荡和光滑区域的计算精度,被广泛应用于各类流动的数值模拟[14–16].随后,Jiang 等[17]引入了新的光滑度量因子,使WENO 格式达到最优精度,该格式被命名为WENO-JS.针对经典的WENO 格式所存在的极值点附近降阶并且耗散过大等问题,典型的改进方法主要包括: Henrick 等[18]提出映射权函数以扩大线性权的范围,使得较大梯度下也能恢复线性权,克服了极值点附近降阶的问题但计算花费较大;Borges 等[19]通过引入高阶全局光滑度量因子构造的形式更为简单的Z 型权.Z 型权可以以较小的计算量获得与原始JS 权基本一致的精度且不存在降阶问题.此外,一些其他常见的WENO 改进格式也被陆续提出,如CWENO[20],WENO-Z+[21]以及HWENO[22]等.
另一种典型的高阶激波捕捉格式是由Deng等[23-24]结合紧致格式[4]和非线性加权技术,在紧致非线性格式CNS (compact nonlinear scheme)[25]基础上构造的加权紧致非线性格式WCNS.WCNS 格式已经成功应用于各种类型的数值模拟,包括边界层转捩及湍流[26]、气动声学[27]、多组分流[28]以及激波-边界层干扰[29]等.总的来说,基于变量插值的WCNS 格式相较于与Jiang 等[17]提出的基于通量函数重构的WENO 格式相比有如下优点[30-33]: (1)相同精度下分辨率更高;(2)数值通量选择更加灵活[34];(3)自由流和涡流保持特性上表现更好[35].
然而,经典的WCNS/WENO 格式仍存在一些明显不足,如灵敏度参数和尺度因子的取值对格式的数值性能有很大影响.例如,由Deng 等[23-24,36]的研究可知,使用WCNS 格式离散Navier-Stokes 方程时,非线性加权函数中灵敏度参数被假定为 ε=1.0×10−6.但使用该格式离散雷诺应力方程时[37],由于雷诺应力的量级很小约为 1.0×10−6,ε=1.0×10−18才能保证计算稳定进行,而 ε=1.0×10−6或 ε=1.0×10−12将会导致计算发散.此外,当使用灵敏度参数ε=1.0×10−12的W E N O 格式重 构小尺 度因子λ=1.0×10−7下的Lax 问题时(Lax 问题的初始条件为Q(x,t=0)=λQ0(x)且Q0(x)=(ρ,ρu,E)),密 度ρ将会在间断附近出现明显的数值振荡[38].因为使用5 阶WENO 格式对小尺度下的不连续函数进行重构的过程中,相对较大的灵敏度参数对相对较小的光滑度量因子占主导地位,使得子模板丧失了自适应性.
为解决上述问题,Don 等[38]引入去尺度函数构建了尺度无关的WENO 格式.受Don 等[38]工作启发,基于WCNS/WENO 格式存在的问题,本文采用函数的平均值构造去尺度函数.通过在WCNS 格式插值过程中引入去尺度函数修正非线性权重中的灵敏度参数,衍生出一种更有效的非线性权重,从而提出了一种不受灵敏度参数和尺度因子控制的尺度无关的WCNS 格式.研究内容主要包括两方面: 首先,探讨WCNS 格式与灵敏度参数和尺度因子的关系;此外,将去尺度函数引入经典的WCNS7-JS/Z/D 格式的非线性权重中以消除尺度的依赖性,构造尺度无关的WCNS 格式(WCNS7-JSm/Zm/Dm).文章的结构如下: 第1 节主要介绍了WCNS 格式离散方法,推导了7 阶D 权函数的形式并且给出了WCNS7-JSm/Zm/Dm 格式插值算法的步骤;第2 节在双精度算法下验证了格式的基本无振荡性质,并在4 精度算法下验证了格式的尺度无关(scale-invariant,Si)性质和极值点(critical point,Cp)性质;在文章的第3 节进行了精度测试,并通过几个一维和二维算例测试了新格式在激波捕捉以及分辨小尺度涡结构等方面的性能;第4 节给出了本文结论.
1 控制方程及其离散
1.1 WCNS 差分格式
考虑如下一维双曲守恒律
其中u(x,t) 是守恒变量,f(u)是通量.考虑在均匀网格上离散,空间坐标xj=jh(j=0,1,2,···,N),网格间距h=(b−a)/N,式(1)的半离散形式为
早期的WCNS 格式[39]常采用Lele[4]提出的单元中心型紧致格式计算一阶导数
式中 κ,a,b,c,d表示系数.如果 κ ≠0,式(3)将需要进行三对角矩阵求逆,此时被称为隐式格式.已有研究[24,40]发现,差分格式的形式,即显式或隐式,对计算结果影响不大,故这里选择更加简单高效的8 阶显式中心差分格式(κ=0),形式如下
1.2 WCNS 插值格式
WCNS 采用非线性加权技术,对上述4 个子模板 (r=4)插值进行加权组合
其中,ωk为非线性权.当 ωk=dk时,上述非线性插值恢复成线性插值格式.dk称为线性权或最优权
1.3 非线性权函数
非线性加权技术是在流场光滑区令非线性权逼近线性权,以保证设计精度,即 ωk=dk;在流场间断区减小不光滑子模板的权重,以避免跨间断插值引起数值震荡和计算不收敛甚至发散等情况,此时 ωk为非线性权,可以通过不同的非线性权函数求解得到.本文使用到的非线性权函数包括经典的JS 权函数[17]
耗散更低的Z 权函数[19]
以及广义上与灵敏度参数无关的D 权函数[44]
权函数中指数p和q通过改变子模板光滑度量因子的偏离程度来影响数值耗散特性,本文默认取p=2q=2. ε 称为灵敏度参数,是避免分母为零的小量,JS,Z 和D 权函数中 ε 通常取1.0×10−6,1.0×10−40和1.0×10−40.βk为子模板的光滑度量,具体形式为各子模板在xj点处1~3 阶导数的平方和
式(11)包含一个线性项L和一个非线性项 Γk
τ
为全模板的高阶全局光滑度量,7 阶WCNS 格式对应的 τ7=|β0+3β1−3β2−β3|[45]在xj点处的泰勒展开式为
式(12)中 Φ 为修正函数,相当于激波探测器: 在流场光滑区,ϕ很小且 Φ=ϕ;在间断区,ϕ很大且 Φ=1,此时,非线性权函数恢复成Z 权函数.根据文献[44]和式(15)可推导修正函数 Φ 的表达式为
1.4 WCNS7-JSm/Zm/Dm 格式
在JS/Z/D 权函数基础上引入去尺度函数,探索了一种更加简单稳定的非线性权函数的构造方法,并将其应用于7 阶WCNS 格式,构造尺度无关的WCNS7-JSm/Zm/Dm 格式,具体步骤如下.
(1)引入去尺度函数 ξ和 µ.
去尺度函数 ξ定义为每个网格点上函数值{fj,,j=0,1,2,···,N}的绝对值和的平均,即
去尺度函数 µ定义为
式中,µ0是避免f(x)=0 且 ξ=0时导致分母为零的情况,在双精 度和四 精度中 µ0分别取1.0×10−40和1.0×10−100.
(2)使用去尺度函数 µ进行修正.
修正Z/D 权函数非线性项中的灵敏度参数
修正D 权函数中的修正函数 Φ
(3)得到修正后的格式.
基于修正后的JS 权构造的WCNS7-JSm 格式为
基于修正后的Z/D 权函数构造的WCNS7-Zm/Dm格式为
WCNS7-JSm/Zm/Dm 格式的非线性权为
(4)根据上述步骤求得非线性权 ωk,插值后可得本文采用特征变量插值,半节点上对流通量的计算使用Rusanov 格式[43],时间格式采用3 阶Runge-Kutta,库朗数为CFL=0.4.
2 性质验证
本节验证了不同灵敏度参数 ε和尺度因子 λ下WCNS 格式的3 种(ENO-,Si-和Cp-)性质.采用双精度算法验证格式的ENO 性质;采用四精度算法分析验证Si 性质和Cp 性质.
2.1 ENO 性质
参照文献[44],这里使用WCNS7-JS/Z/D 格式在 ε=1.0×10−6和ε=1.0×10−40时分别模拟小尺度λ=1.0×10−7和正常尺度λ=1下的Lax 问题,以验证WCNS7-JS/Z/D格式在不同灵敏度参数和尺度因子下的ENO 性质.
Lax 问题的初始条件为Q(x,t=0)=λQ0(x),Q0(x)=(ρ,ρu,E)且E=p/γ −1 +ρu2/2,即[46]
计算终止时间为t=1.3,网格数为N=200.
图1和图2 给出了 在 ε=1.0×10−6和ε=1.0×10−40时分别使用WCNS 格式求解Lax 问题的计算结果,其中红色实线和蓝色实线分别为 λ=1,λ=1.0×10−7时的计算结果,黑色虚线代表精确解.ε=1.0×10−6时,3 种格式的密度分布曲线基本相同,因此图1 仅给出WCNS7-JS 格式的密度分布曲线;ε=1.0×10−40时,WCNS7-JS 与WCNS7-Z 格式密度分布曲线基本相同但与WCNS7-D 格式不同,故图2 给出WCNS7-JS 和WCNS7-D 格式的计算结果.

图1 ε=1.0×10−6 时Lax 问题的密度分布曲线Fig.1 Density distribution curves of the Lax problem with ε=1.0×10−6
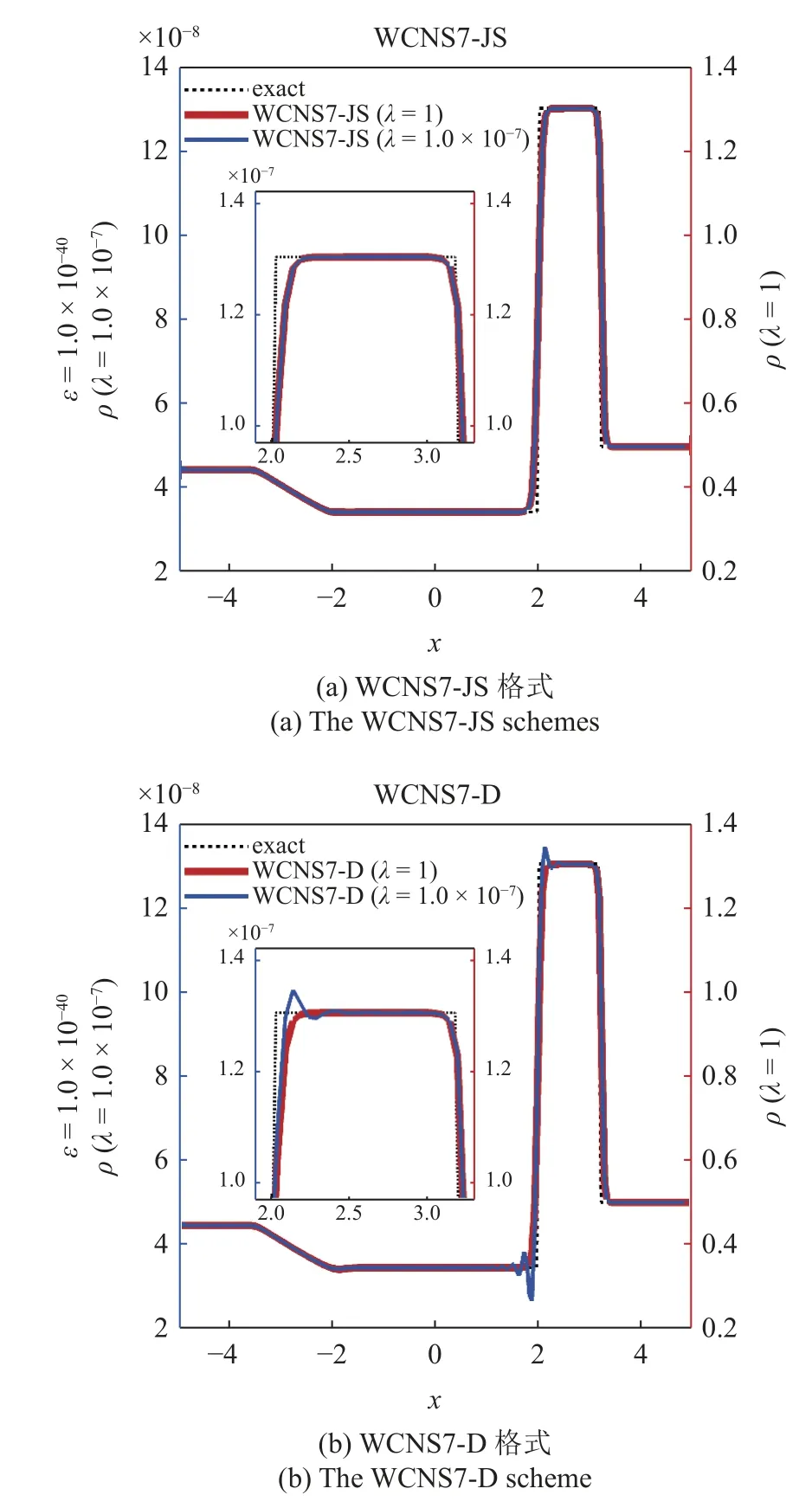
图2 ε=1.0×10−40 时Lax 问题的密度分布曲线Fig.2 Density distribution curves of the Lax problem with ε=1.0×10−40
从图1 和图2 中可以看出,当 λ=1时,无论灵敏度参数 ε如何变化,密度ρ都满足ENO 性 质.当λ=1.0×10−7时,ε=1.0×10−6下的WCNS7-JS/Z 格式在不连续区域附近会出现明显的数值振荡;WCNS7-D格式则是不管灵敏度参数如何取值,在不连续区域附近都会出现数值振荡.因此,WCNS7-D 格式在小尺度下对任意灵敏度参数都不满足ENO 性质,而WCNS7-JS/Z 格式仅在小尺度和较大的灵敏度参数下不满足ENO 性质.综上,灵敏度参数和尺度因子的取值对WCNS 格式的ENO 性质有显著的影响.
图3 展示的是 ε=1.0×10−6和ε=1.0×10−40时的WCNS7-Dm 格式(WCNS7-JSm/Zm/Dm 格式的密度分布曲线基本相同) 求解 λ=1 和λ=1.0×10−7下Lax 问题的密度分布图.从图3 反映的结果可以看出,不管灵敏度参数和尺度因子如何变化,WCNS7-JSm/Zm/Dm 格式都满足ENO 性质,即某种程度上可以认为修正后的格式与灵敏度参数和尺度因子的取值无关.

图3 ε=1.0×10−6和 ε=1.0×10−40 时使用WCNS7-Dm 格式求解Lax 问题的密度分布曲线Fig.3 Density distribution curves of the Lax problem computed by the WCNS7-Dm scheme with ε=1.0×10−6 and ε=1.0×10−40
2.2 Si 性质
接下来验证WCNS 格式的Si 性质.在继续进行数值模拟之前,需要给出Si 性质和弱Si 性质的定义.
定义1:如果WCNS 格式的非线性插值算子W[·] 对任意尺度因子 λ ∈R和任何给定函数f都满足W[λf]=λW[f],称此WCNS 格式是尺度无关的,即满足Si 性质.
然而,Si 性质要求的条件非常严格,故引入临界尺度因子 λ∗和弱Si 性质.
定义2:如果存在临界尺度因子 λ∗≥0 且 λ∗∈R使得WCNS 算子W[·] 对任何给定函数f和任意两个尺度因子 λ1,λ2且λ1,λ2∈S∞={λ|λ ∈R,|λ|≥λ∗}都满足 λ2W[λ1f]=λ1W[λ2f],则称此WCNS 格式是弱尺度无关的,即满足弱Si 性质.
计算L∞范数下Si 的误差ESi(λ)来验证WCNS格式的(弱)Si 性质,ESi(λ)的形式如下
式中,ϵ0称为机器舍入误差,λ∞是参考尺度因子,λ ∈[1.0×10−19,1.0×1019].因为参考尺度因子 λ∞=1.0×1020足够大,故参考WCNS 算子W[λ∞f]/λ∞可以假设其计算是与尺度无关的.
为验证WCNS 格式的Si 性质,本节计算了求解双曲守恒律中经常遇到的一些典型函数[38]: (1)C∞正弦函数;(2)C0分段光滑ReLU;(3) Heaviside 函数,函数的定义如下
如图4~图6 给出了6 种WCNS 格式分别求解正弦函数、ReLU 函数和Heaviside 函数在尺度因子λ ∈[1.0×10−19,1.0×1019] 范围内的Si 误差ESi(λ),其中 ε=1.0×10−6(上行)、ε=1.0×10−40(下行),并且有3 套不同的网格数.从图中可以看出,对于任意 λ误差ESi(λ)通常很小,在双精度算法中,计算误差与机器舍入误差 ϵ0≈1.0×10−16将无法区分,故需要在四精度算法中进行,机器的舍入误差为 ϵ0≈1.0×10−34.
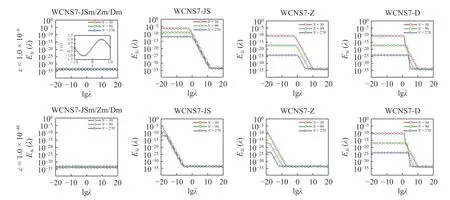
图4 3 套网格单元数 N 下使用WCNS 格式计算Sine 函数 f1(x) 的Si 误差 E Si(λ),λ ∈[1.0×10−19,1.0×1019],ε=1.0×10−6 (上行)和ε=1.0×10−40 (下行)Fig.4 The Si-error E Si(λ) of the Sine function f1(x) calculated by the WCNS schemes with ε=1.0×10−6 (top row),ε=1.0×10−40 (bottom row),and different scale factors λ ∈[1.0×10−19,1.0×1019] for three number of cells N

图5 3 套网格单元数 N 下使用WCNS 格式计算 R eLU 函数 f2(x) 的Si 误差 E Si(λ),λ ∈[1.0×10−19,1.0×1019],ε=1.0×10−6 (上行)和ε=1.0×10−40 (下行)Fig.5 The Si-error E Si(λ) of the R eLU function f2(x) calculated by the WCNS schemes with ε=1.0×10−6 (top row),ε=1.0×10−40 (bottom row),and different scale factors λ ∈[1.0×10−19,1.0×1019] for three number of cells N

图6 3 套网格单元数 N 下使用WCNS 格式计算Heaviside 函数 f3(x) 的Si 误差 E Si(λ),λ ∈[1.0×10−19,1.0×1019],ε=1.0×10−6 (上行)和ε=1.0×10−40 (下行)Fig.6 The Si-error E Si(λ) of the Heaviside function f3(x) calculated by the WCNS schemes with ε=1.0×10−6 (top row),ε=1.0×10−40 (bottom row),and different scale factors λ ∈[1.0×10−19,1.0×1019] for three number of cells N
首先观察尺度无关的WCNS 格式,如图4~图6(左),对于任意的尺度因子 λ和灵敏度参数 ε,测试函数 {fl(x),l=1,2,3}的 误差ESi(λ)基 本上为 1.0×10−34,这说明WCNS7-JSm/Zm/Dm 格式满足Si 性质.其次,观察经典的WCNS 格式,如图4~图6(中和右),误差ESi(λ)明 显取决于 λ 并 且在较小程度上也取决于 ε,例如,对于分段光滑ReLU 函数f2(x)和Heaviside 函数f3(x),临界尺度因子 λ∗随着灵敏度参数 ε的减小而减小.具体而言,对于Heaviside 函数f3(x),当灵敏度参数从 1.0×10−6减小到1.0×10−40时,WCNS7-JS 和WCNS7-Z格式的临界尺度因子 λ∗从O(1014)减少 到O(10−3);同理,ε从1.0×10−6减 小到1.0×10−40时,WCNS7-D 格式的临界尺度因子 λ∗从O(1014)减少到O(100),这说明经典的WCNS 格式只满足弱Si 性质.最后,结合文献[38]可以得出如下结论:
(1) 对于任意给定的灵敏度参数 ε,WCNS7-JS 和WCNS7-Z 格式在临界尺度因子时满足弱Si 性质;
(2) 对于任意给定的灵敏度参数 ε,WCNS7-D格式在临界尺度因子时满足弱Si 性质;
(3)WCNS7-JSm/Zm/Dm 格式满足Si 性质且与 ε和 λ无关,故被称为尺度无关的WCNS 格式.
2.3 Cp 性质
为讨论WCNS 格式的Cp 性质,结合文献[21,44]给出极值点、Cp 性质的定义.
定义3:若f′(xc)=...=且ncp>0,称f(x)在xc处有一 个ncp阶的极值点.若ncp=0,则xc不是极值点.
定义4:对于给定指数p和灵敏度参数 ε,如果一个 (2r−1) 阶的WCNS 格式直到第r阶的极值点处逼近光滑函数的一阶导数时都保持其最优精度,称此WCNS 格式满足Cp 性质.
为研究新格式在不同尺度因子 λ下对存在高阶极值点的光滑函数所能达到的收敛精度,使用如下测试函数
式中 λ >0,函数在x=0且ncp=n处有一个n阶极值点.图7 给出了当 λ=1,ncp=1,2,3,4时WCNS 格式在 ε=1.0×10−6和 ε=1.0×10−40时的L∞误差和收敛阶,线条颜色(蓝/粉/橙/红/绿/黑)分别代表WCNS7-(JS/Z/D/JSm/Zm/Dm)格式.表1 给出了 λ=1.0×10−7和 λ=100 时,ε=1.0×10−40且ncp=3 下的L∞误差和WCNS 格式的收敛阶,由于WCNS7-JS 和WCNS7-JSm 格式的误差值和收敛阶大致相同,WCNS7-Z和WCNS7-Zm 格式的误差值和收敛阶也基本相同,因此,表1 仅给出了WCNS-JSm/Zm/D/Dm 格式的结果.根据图7、表1 以及参考文献[38,44]可以得到如下结论.
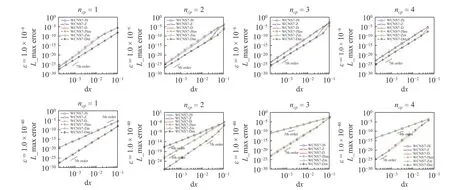
图7 在极值点 n cp=n=1,2,3,4 下WCNS 格式的收敛精度和 L∞ 误差,且 λ=1,ε=1.0×10−6 (上行),ε=1.0×10−40 (下行)Fig.7 L∞ error of the WCNS schemes with ε=1.0×10−6 (top row),ε=1.0×10−40 (bottom row),and the scale factor λ=1 for ncp=n=1,2,3,4
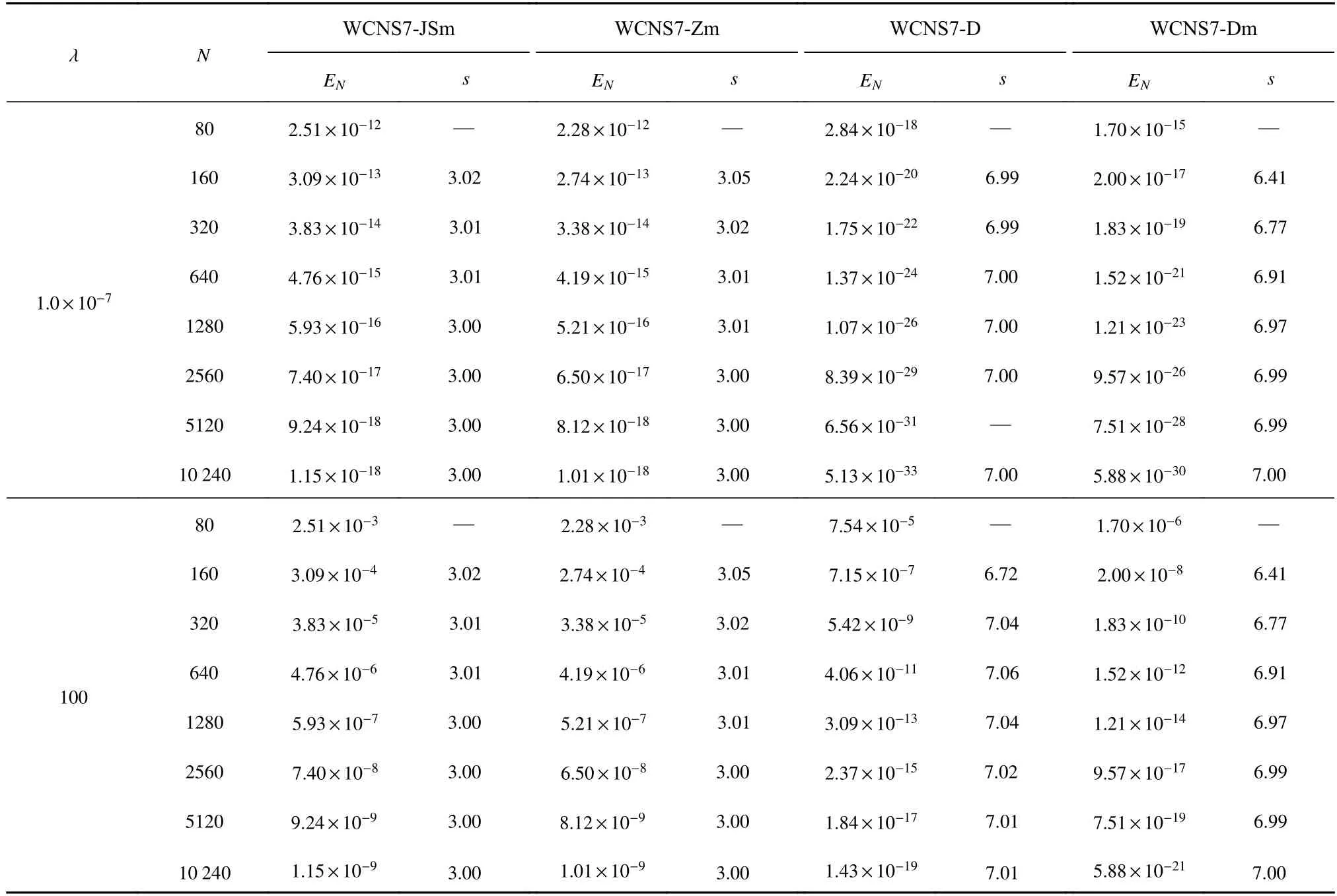
表1 WCNS 格式在 ε=1.0×10−40,n cp=3 时的 L∞ 误差 E N 和收敛阶 O(∆xs)Table 1 L∞ error E N,and order of accuracy O (∆xs) of WCNS schemes with ε=1.0×10−40 and ncp=3
(1)当灵敏度参数较大时 ε=1.0×10−6,6 种WCNS格式都能达到设计精度O(∆x7).
(2) 当灵敏度参数较小时 ε=1.0×10−40,仅有WCNS7-D/Dm 格式能够达到设计精度O(∆x7),WCNS7-JS/JSm 和WCNS7-Z/Zm 格式只有在ncp≥3时精度才能达到O(∆xncp).
(3)对于小灵敏度参数 ε=1.0×10−40,WCNS7-Z/Zm 格式只有在ncp=1时能够达到设计精度;WCNS7-JS/JSm 格式在ncp=1,2,3,4时都无法达到设计精度.
(4)对于任意灵敏度参数 ε,WCNS7-D/Dm 格式都能满足Cp 性质并且能保持最优精度而WCNS7-JS/JSm 和WCNS7-Z/Zm 格式则不能.
综上,WCNS7-D/Dm 格式比WCNS7-JS/JSm和WCNS7-Z/Zm 格式表现出更好的精度特性.这些结论与Don 等[38]的观察是一致的,尽管基于通量重构的WENO 格式与基于变量插值的WCNS 格式的离散化过程存在明显差异,但这两种格式在Cp 性质方面没有明显的差异.
3 数值实验
接下来的数值实验将进一步研究新格式的性质以及新格式在典型算例中的表现.数值实验包括一维线性对流方程的精度测试,一维Euler 方程,包括Lax 问题[46]、Sod 问题[47]、激波密度波相互作用问题[19]以及爆炸波相互作用问题[48],以及二维Euler方程,如二维Riemann 问题[49]、双马赫反射[48]以及Richtmyer-Meshko 不稳定性问题[50].所有算例均在双精度算法下进行并采用特征变量插值和比热比γ=1.4的量热完全气体模型.
3.1 精度测试
求解3 种尺度因子(λ=1.0×10−7,1,100) 下的线性对流方程以测试 ε=1.0×10−6和ε=1.0×10−40时WCNS 格式的收敛精度,由于两种灵敏度参数下的结果相似,故省略了 ε=1.0×10−6时的结果.测试用到高斯波函数
计算一个周期t=2,计算域x∈[−1,1],左右边界设为周期性边界且库朗数为CFL=0.1.简便起见,这里仅给出WCNS7-D 和WCNS7-Dm 格式的计算结果,如表2 所示.数据结果表明,WCNS7-Dm 格式的收敛精度与经典的WCNS7-D 格式的收敛精度基本一致,并且随着网格加密都可以达到设计(7 阶)精度.WCNS7-JSm 和WCNS7-Zm 格式有相同的结论.

表2 WCNS7-D/Dm 格式的误差值和收敛阶 (ε=1.0 × 10−40)Table 2 Error and accuracy statistics for WCNS7-D/Dm schemes (ε=1.0 × 10−40)
3.2 一维Euler 方程
3.2.1 Lax 和Sod 问题
Lax 问题的初始条件如式(25).Sod 问题的初始条件[47]为
计算终止时间为t=0.2,网格数为N=200.
图8 给出了使用灵敏度参数为 1.0×10−6和1.0×10−40的WCNS 格式求解3 种尺度(λ=1.0×10−7,1,100)下Lax 问题的计算结果.由于Lax 和Sod 问题的结论相同,为简便起见,图9 仅给出了 ε=1.0×10−40时使用WCNS格式计算 λ=1.0×10−7下的Sod 问题的结果.观察图8 和图9,对于 λ=1和λ=102,6 种WCNS 格式的表现基本相同,均没有出现数值振荡并满足ENO 性质;当 λ=1.0×10−7时,WCNS7-J Sm/Zm/Dm 格式没有出现数值振荡,依旧保持ENO性质,而WCNS7-JS/Z/D 格式在不连续区域附近出现了明显的数值振荡,失去了ENO 性质,这就验证2.1 节的分析结果.
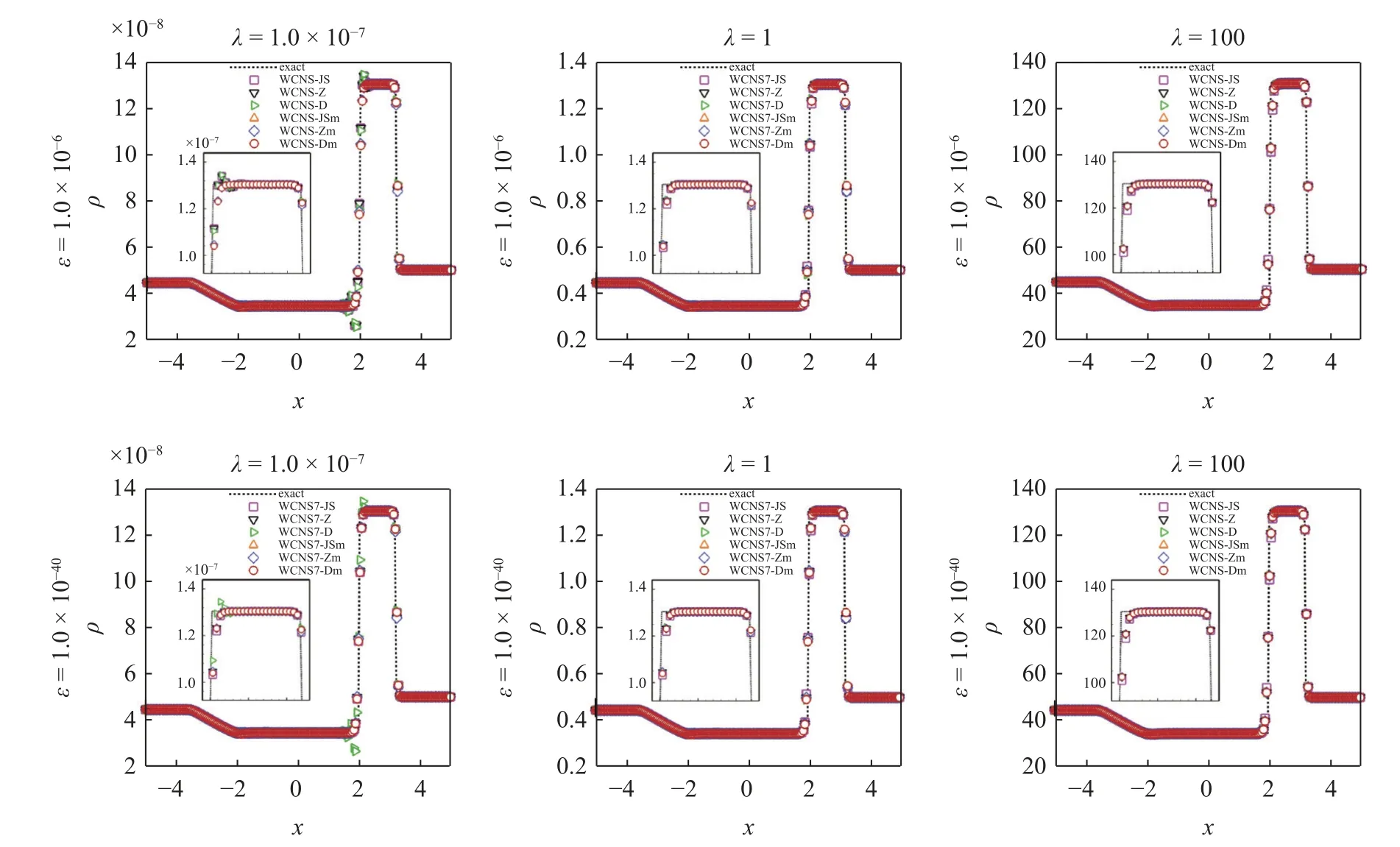
图8 ε=1.0×10−6和 ε=1.0×10−40 时分别使用WCNS 格式计算 λ=1.0×10−7,1,100 下的Lax 问题Fig.8 Density of the Lax problem computed by the WCNS schemes with ε=1.0×10−6 and ε=1.0×10−40 for λ=1.0×10−7,1,100
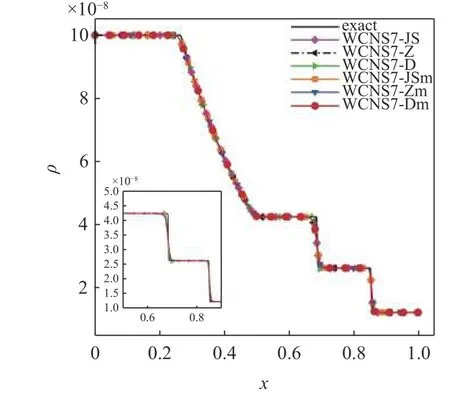
图9 ε=1.0×10−40 时使用WCNS 格式计算 λ=1.0×10−7 的Sod 问题Fig.9 Density of the Sod problem computed by the WCNS schemes with ε=1.0×10−40 for λ=1.0×10−7
3.2.2 激波密度波相互作用问题
该问题描述一道马赫数为3 的右行激波与一系列密度波相互作用,可用来测试格式的激波捕捉能力、耗散性、数值稳定性和高频波分辨率,初始条件为[19]
其中,a=0.2,x0=−4 且k=5.计算终 止时间t=5,网格数N=600.
简便起见,图10 仅给出了 λ=1.0×10−7且 ε=1.0×10−40时6 种WCNS 的计算结果.观察图10(b),注意到WCNS7-D 格式(绿色)曲线在区间[0.73,0.8]上存在严重的过冲,这可能与WCNS7-D 格式低耗散性质有关.其他5 种格式没有明显的过冲或下冲现象,这说明WCNS7-Dm 格式相较于WCNS7-D 格式实现了对过冲较好的抑制作用.曲线过冲或下冲可能会增大误差,影响计算的稳定性,故除存在过冲现象的WCNS7-D 格式(绿色),WCNS7-Dm 格式(红色)相较于其他格式表现略好且分辨率略高.

图10 ε=1.0×10−40 时使用WCNS 格式计算 λ=1.0×10−7 激波密度波问题Fig.10 Density of the shock-density wave interaction problem computed by the WCNS schemes with ε=1.0×10−40 for λ=1.0×10−7
3.2.3 爆炸波相互作用问题
接下来计算爆炸波相互作用问题[48],初始条件为
计算终止时间为t=0.038,网格数N=400.
图11 给出 λ=1.0×10−7和 ε=1.0×10−40下的计算结果.观察图11(b),注意到WCNS7-D 格式(绿色)曲线在区间 [ 0.73,0.8]上存在微弱的下冲和过冲,其他5 种格式表现良好均不存在过冲或下冲.同样可以看出,WCNS-Dm 格式相较于WCNS-D 格式实现了对过冲和下冲行为较好的抑制作用.除存在过冲和下冲现象的WCNS7-D 格式(绿色),WCNS7-Dm 格式(红色)相较于其他格式表现略好且分辨率略高.此外,在相同条件下使用网格数N=800重新计算该问题,如图12 所示.观察图11 和图12,可以看出两种网格分辨率下的现象基本相同.总的来说,WCNS7-Dm 格式性能表现最优.
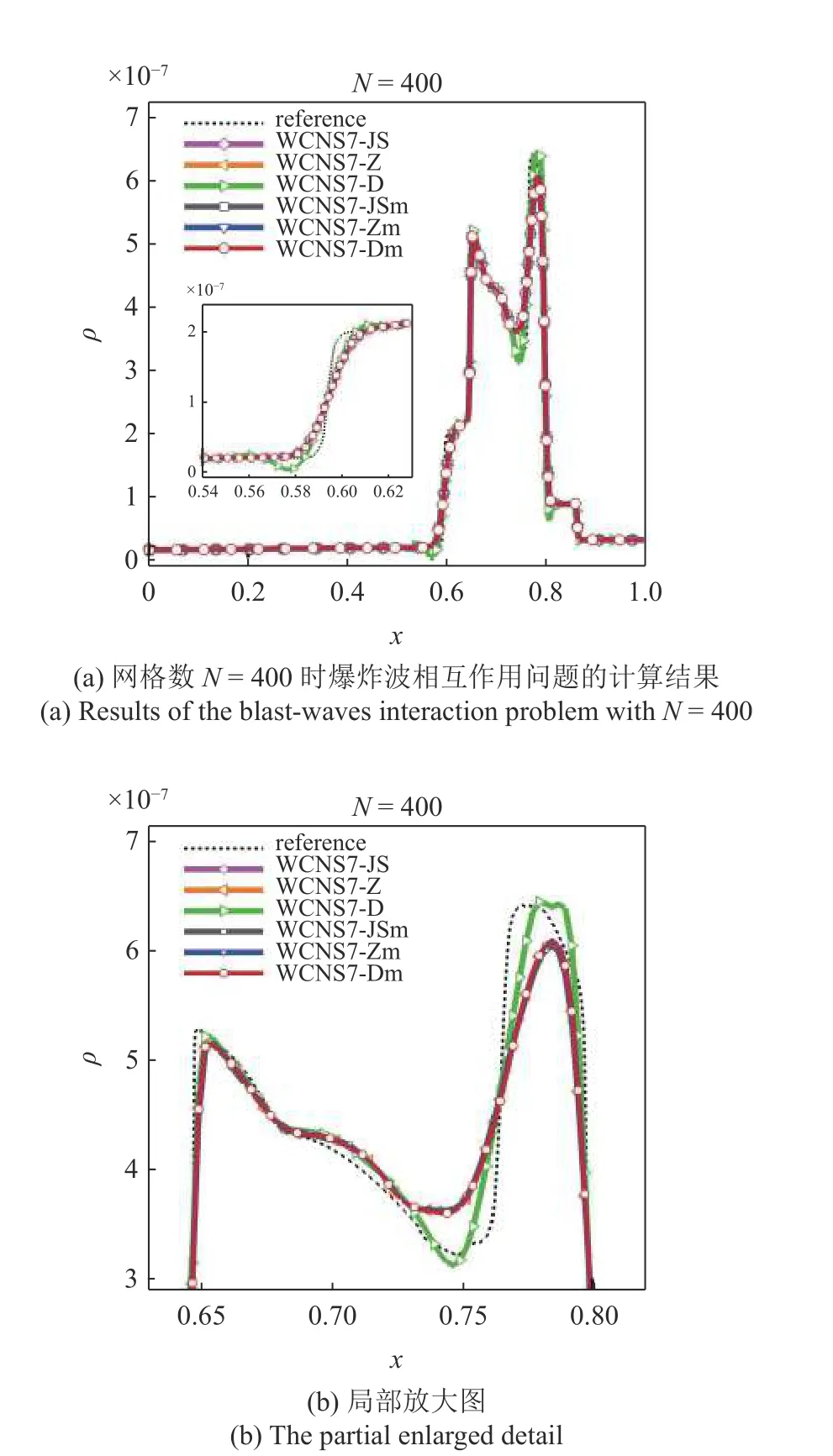
图11 N=400 时使用WCNS 格式计算爆炸波相互作用问题Fig.11 Density of the blast-waves interaction problem computed by the WCNS schemes with N=400
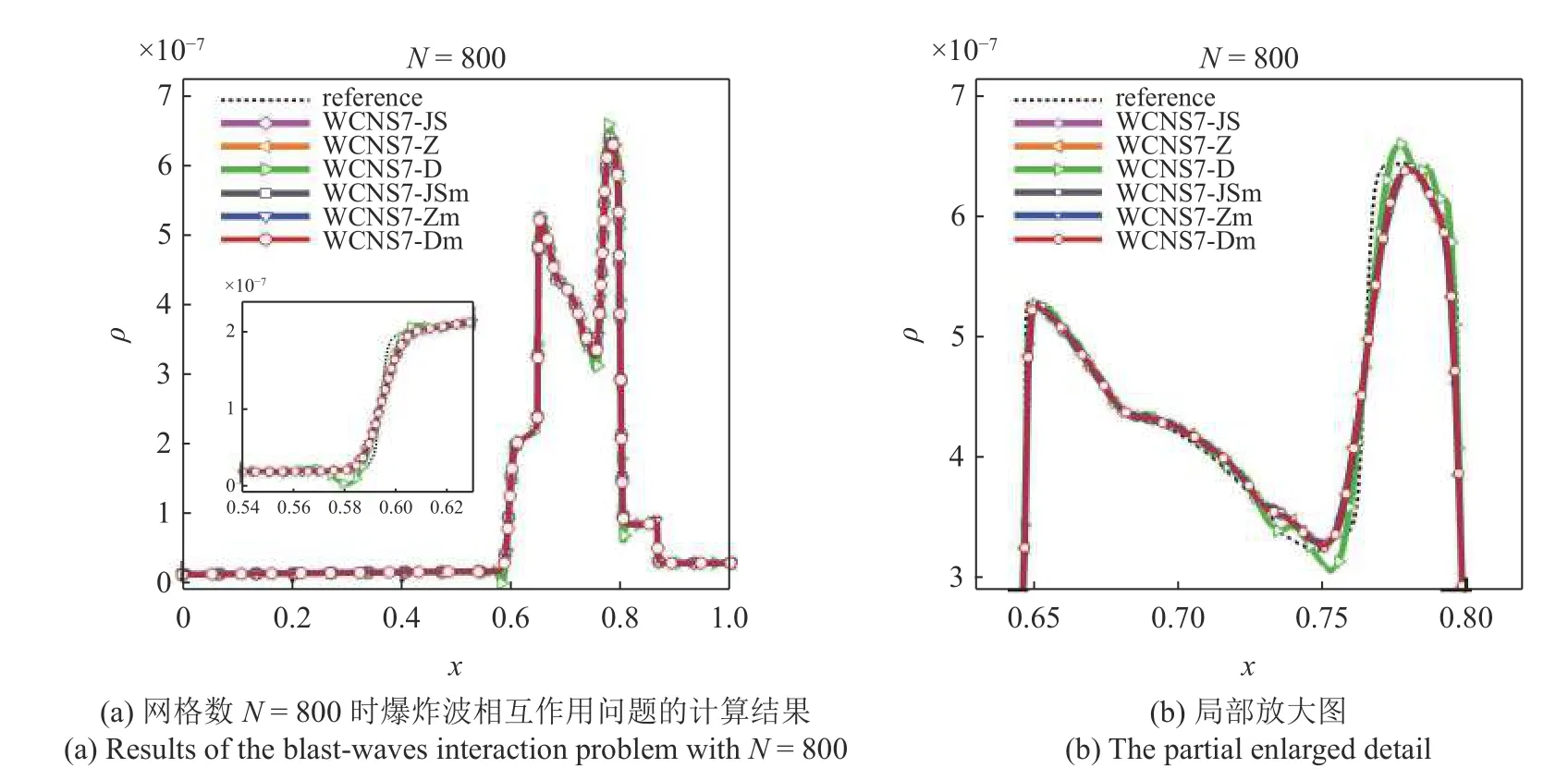
图12 N=800 时使用WCNS 格式计算爆炸波相互作用问题Fig.12 Density of the blast-waves interaction problem computed by the WCNS schemes with N=800
3.3 二维Euler 方程
3.3.1 二维Riemann 问题
该问题包含多尺度的流场结构,可测试数值格式的多尺度分辨率.使用Riemann 问题[49]中的构型3 和构型6,这两种构型的流场中包含丰富的小尺度结构,可以更好地测试数值格式分辨小尺度结构的能力.计算域为 [ 0,1]×[0,1],构型3 的初始条件为
计算终止时间为t=0.8,网格数量为 4 00×400.
图13 给出了 ε=1.0×10−40时WCNS7-JSm/Zm/Dm格式的计算结果,密度等值线是 [ 0.1,1.8]×λ等间距的30 条.观察图13,WCNS7-JSm/Zm/Dm 格式都可以基本无振荡地捕捉不连续,并且在两种不同的尺度因子下,λ=1 (左) 和λ=1.0×10−7(右),密度等值线分布基本相同.ε=1.0×10−6时的WCNS7-JSm/Zm/Dm 格式也有类似的结果,简便起见,在此省略.结果表明,WCNS7-JSm/Zm/Dm 格式同时满足Si 性质和ENO 性质.构型6 的初始条件为
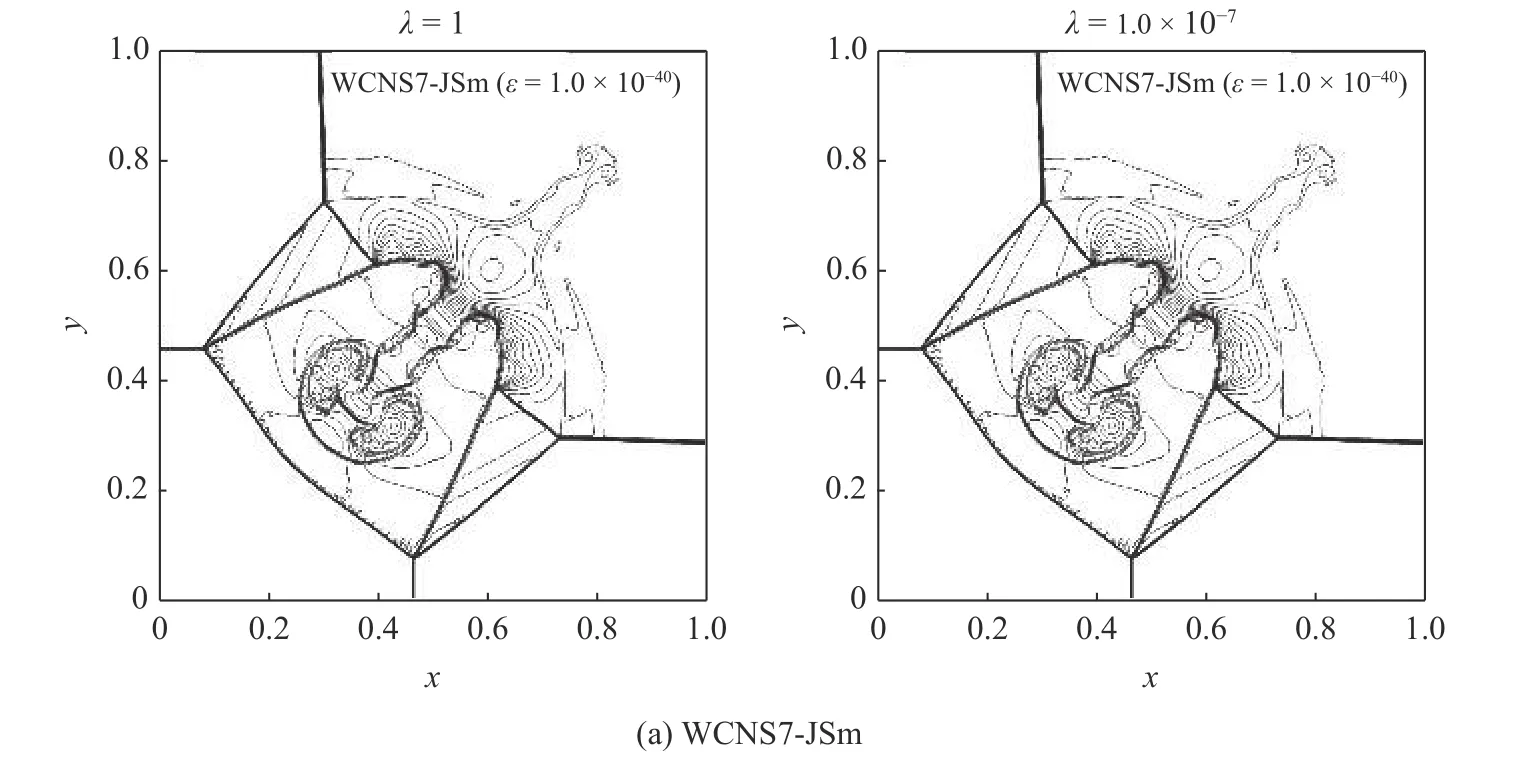
图13 ε=1.0×10−40 时使用WCNS 格式计算Riemann 问题中的构型3Fig.13 Density of the configuration 3 of 2-D Riemann problems computed by the WCNS7-JSm/Zm/Dm schemes with ε=1.0×10−40
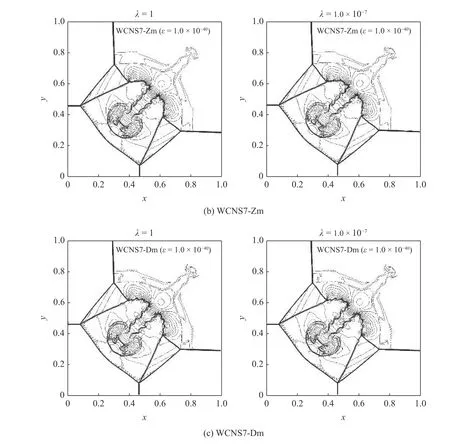
图13 ε=1.0×10−40 时使用WCNS 格式计算Riemann 问题中的构型3 (续)Fig.13 Density of the configuration 3 of 2-D Riemann problems computed by the WCNS7-JSm/Zm/Dm schemes with ε=1.0×10−40 (continued)
计算终止时间为t=0.3,网格数量为 4 00×400.
图14 比较了小尺度因子 λ=1.0×10−7下灵敏度参数分别为 1.0×10−6和 1.0×10−40时的WCNS7-D和WCNS-Dm 格式的计算结果,密度等值线是[0.1,2.9]×λ等间距的40 条.观察图14,WCNS7-D格式图14(a) 沿滑移线附近的振荡更加明显,而WCNS7-Dm 格式图14(b)则依旧能够基本无振荡地捕捉不连续.

图14 ε=1.0×10−40 时使用WCNS7-D/Dm 格式计算 λ=1.0×10−7 下的二维 Riemann 问题中的构型6Fig.14 Density of the configuration 6 of 2-D Riemann problems computed by the WCNS7-D/Dm schemes with λ=1.0×10−7 and ε=1.0×10−40

图14 ε=1.0×10−40 时使用WCNS7-D/Dm 格式计算 λ=1.0×10−7 下的二维 Riemann 问题中的构型6 (续)Fig.14 Density of the configuration 6 of 2-D Riemann problems computed by the WCNS7-D/Dm schemes with λ=1.0×10−7 and ε=1.0×10−40(continued)
3.3.2 双马赫反射
在双马赫反射问题[48]中,马赫数为10 的斜激波以60°角入射到静止平板上并继续传播,所产生的流场中包含丰富的旋涡结构和十分复杂的激波反射,可用来测试数值格式捕捉激波和回流区小尺度结构等能力.计算域为 [ 0,4]×[0,1],初始条件为
计算终止时间为t=0.2,网格数量为 9 61×241.
图15 给出了 ε=1.0×10−40时的WCNS7-Dm 格式的计算结果,密度等值线是[2,23]× λ等间距的39 条.观察图15,WCNS7-Dm 格式在 λ=1.0×10−7和 λ=1的情况下都可以基本无振荡地捕捉不连续,并且两种尺度因子下的密度等值线分布基本相同.WCNS7-JSm 和WCNS7-Zm 格式均有类似结果,简便起见,在此省略.这说明尺度无关的WCNS7-JSm/Zm/Dm 格式同时满足Si 性质和ENO 性质.
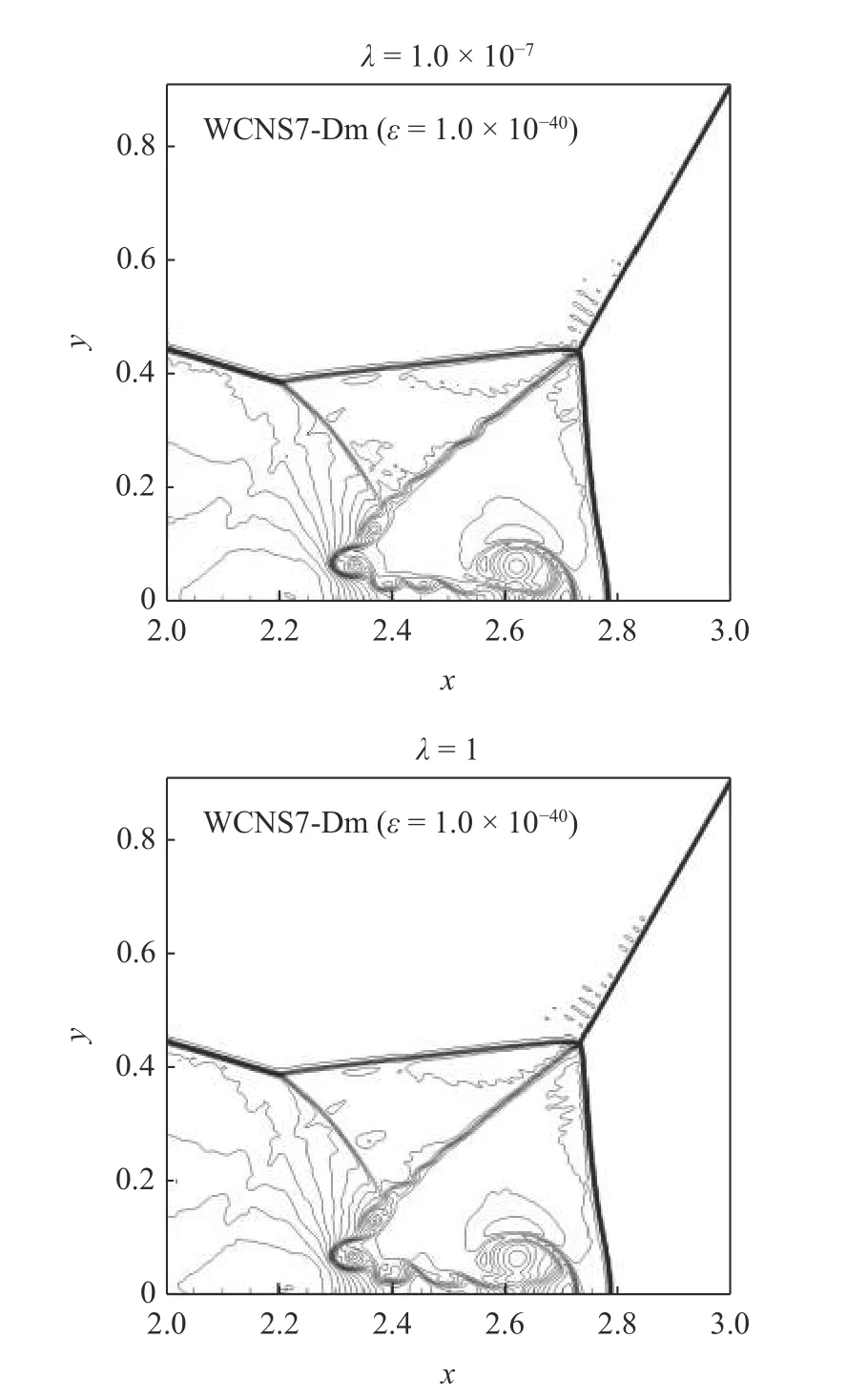
图15 ε=1.0×10−40 时使用WCNS7-Dm 格式计算双马赫反射问题Fig.15 Density of the double Mach reflection problem computed by the WCNS7-Dm scheme with ε=1.0×10−40
3.3.3 Richtmyer-Meshko 不稳定性问题
Richtmyer-Meshko 不稳定性问题[50]实际上是激波加速两种密度不同的流体所导致的界面不稳定现象.计算域为 [ 0,4]×[0,1],初始条件为
计算终止时间为t=9,网格数量为 3 21×81.
图16 仅给出了 ε=1.0×10−40时WCNS7-Dm 格式在 λ=1.0×10−7和 λ=1下的计算结果,密度等值线是 [ 2,7.5]×λ等间距的24 条.结论与3.3.2 节相同.
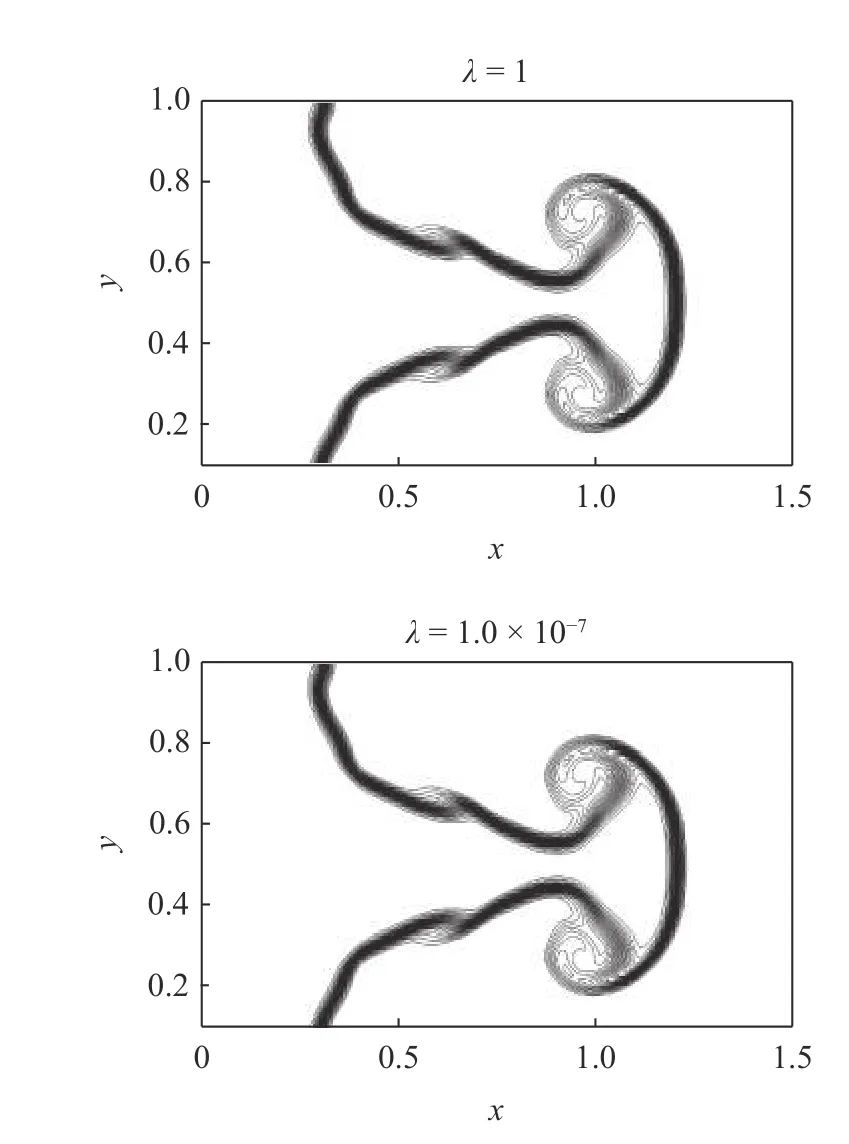
图16 ε=1.0×10−40 时使用WCNS7-Dm 格式计算Richtmyer-Meshko 不稳定性问题Fig.16 Density of the Richtmyer-Meshkov instability problem computed by the WCNS7-Dm scheme with ε=1.0×10−40
4 结论
本文通过一系列的数值实验验证了尺度无关的WCNS7-JSm/Zm/Dm 格式的ENO 性质、Si 性质和Cp 性质,对比了新格式与经典的WCNS 格式在激波捕捉能力和对复杂流场结构的分辨率上的表现.首先,从操作层面而言,新格式只需要在WCNS格式基础上,使用函数的平均值构建去尺函数,再引入去尺度函数来修正非线性权重中的灵敏度参数,这个过程并未引入任何复杂性.
其次,从设计思路来看,经典的WCNS 格式不满足Si 性质,因为小尺度下函数的插值更容易在不连续区域附近产生数值振荡,而尺度无关的WCNS 格式则是使格式性能与尺度因子和灵敏度参数无关,首先将去尺度函数引入WCNS7-JS 和WCNS7-Z 格式的权重中以消除尺度的依赖性,衍生出尺度无关的WCNS7-JSm 和WCNS7-Zm 格式,但WCNS7-JSm 和WCNS7-Zm 格式仅满足ENO 性质和Si 性质,不满足Cp 性质,为解决极值点附近出现降阶现象,基于WCNS7-Z/Zm 格式,又提出了WCNS7-D/Dm 格式.
此外,从计算结果来看,新格式随着网格加密能够达到最优精度;WCNS7-Dm 格式满足所有3 种(ENO-,Si-和Cp-)性质而不受灵敏度参数和尺度因子的影响;WCNS7-JSm/Zm 格式满足ENO 性质、Si 性质和弱Cp 性质;经典的WCNS7-JS/Z/D 格式只满足上述3 种性质中的某些性质或较弱的情况.
综上,尺度无关的WCNS 格式性能与灵敏度参数和尺度因子无关,解决了经典的WCNS 格式在小尺度下易产生数值振荡的问题并且在激波捕捉能力和对复杂流场结构的分辨率上表现良好,以期为WCNS 格式的改进和应用提供新的思路.接下来的工作将从两个方面开展,首先从应用层面,将进一步测试尺度无关的WCNS 格式在具体算例中的数值表现.其次从数值分析层面,去尺度函数的优化工作也是下一步研究的重点.
