基于深度神经网络的横流转捩预测1)
2023-02-25胡震宇王子路陈坚强袁先旭向星皓
胡震宇 王子路 陈坚强 袁先旭 向星皓
(空气动力学国家重点实验室,四川绵阳 621000)
引言
转捩是一个连续演化的流动过程,是一种从简单分层稳定状态向复杂多变湍流状态的过渡[1].转捩研究不仅具有重要的理论意义,还具有重要的工程应用价值.转捩过程受多种模态影响[2],由于其复杂性,将长期作为现代流体力学重点关注的前沿领域而存在[3].
关于流体力学的研究,飞行试验、地面实验具有直观、真实的特点,能够为稳定性理论、数值计算提供较为准确的验证数据[4-6].直接数值模拟(direct numerical simulation,DNS)方法[7-10]直接求解N-S 方程,能够准确捕捉流场结构,但对计算资源要求较高;大涡模拟(large eddy simulation,LES)方法[11]对大尺度涡进行解析、对小尺度涡进行模化,计算结果较为准确,但依然要求较高的网格分辨率;雷诺平均N-S (Reynolds averaged Navier-Stokes,RANS)方法[12-14]中,利用湍流模型封闭雷诺应力项,降低了对网格分辨率的要求,应用较为广泛.
基于RANS 方法的k-ε,k-ω,SSTk-ω等传统湍流模型,能够一定程度上满足工程需要,但无法捕捉边界层内转捩的过程.对于转捩过程的描述,通常用到间歇因子γ[15]
式中,I(x,y,z,t)表征某一空间点在某一时刻的流动状态,处于湍流状态时I(x,y,z,t)=1,处于层流状态时I(x,y,z,t)=0.
间歇因子γ表征某一空间点处于湍流状态的时间占总时间T的比例.通过求解间歇因子γ的输运方程,可以获得间歇因子γ在流场中的分布情况.转捩模型通过对间歇因子γ或其他参数进行建模,并与湍流模型耦合求解,实现对转捩过程的预测.
Steelant 等[15]针对bypass 转捩,构建了间歇因子γ的输运方程,计算结果能够与实验数据较好地吻合.目前应用较广的转捩模型,也是通过构建间歇因子γ的输运方程来实现转捩预测的.例如Langtry等[16]建立的γ-Reθ转捩模型,王亮等[17]建立的k-ω-γ转捩模型.
神经网络通过模仿生物的大脑神经元结构和功能,使计算机对数据信息能够进行智能处理,构建复杂、非线性映射关系[18].相比于求解输运方程,深度神经网络(deep neural networks,DNN)所需的计算资源更少,显著提高计算效率,在湍流模型化工作中具有良好的前景[19-20].
Templeton 等[21]提出了张量基神经网络 (tensor based neural network,TBNN) 架构,并用于预测低速的管流、周期山流动.任海杰等[22]基于文献[21]搭建的 TBNN 内核构建了神经网络模型,并针对Boussinesq 假设难以准确捕捉雷诺应力各向异性张量的问题,利用Pope[23]给出的各向异性张量b与基张量T(n)之间的本构关系,构建了张量不变量λ1~λ5与标量函数g(n)间的映射关系,对高超声速平板进行预测,得到的各向异性张量分布与DNS 计算结果吻合较好.Wei 等[24]提出了基于深度强化学习的流体力学微分方程统一求解框架,求解了流体力学Burgers 方程、稳态N-S 方程.Sekar 等[25]基于深度学习方法,针对具有不同外形的机翼,构建了绕流流场预测模型.Zhu 等[26]通过径向基函数神经网络以及深度神经网络,对涡黏系数进行了预测,并用于封闭湍流模型.张珍等[27]提出了一种基于组合神经网络预测涡黏系数和雷诺应力各向异性张量的修正方法,对雷诺应力的线性部分进行了求解.Beetham等[28]运用传统 RANS 方法求解RANS 模型线性部分,运用神经网络预测RANS 模型非线性部分,但缺乏足够精度.
目前人工智能在计算流体力学领域的研究,主要集中在重构或修正湍流涡黏性和雷诺应力[29].随着学科间的交叉与发展,将神经网络应用于边界层转捩问题求解,成为一个新的热门研究方向.郑天韵等[29]基于深度残差网络(deep residual network,ResNet),构建了间歇因子γ与流场平均量间的映射关系,并与spallart allmaras (SA)湍流模型耦合,发展了一种类代数转捩模型,性能接近SST-γ-Reθ模型,但收敛到同一精度节省了超过30% 的计算成本.Foroozan 等[30]运用Johns Hopkins 湍流数据库(Johns Hopkins turbulence databases,JHTDB)构建了训练数据集,采用无监督机器学习的方法,实现了对边界层bypass 转捩的识别.
本文DNN 基于Pytorch 平台.数值计算基于Chant 2.0 平台[31-32],该平台部署了横流拓展γ-Reθ转捩模型[33].横流拓展γ-Reθ转捩模型在原始γ-Reθ转捩模型[16]上进行改进,在NLF(2)-0415 后掠翼、6 : 1 标准椭球体、镰刀翼和DLR-F4 翼身组合体等典型横流转捩算例上均有着良好的计算效果,能做到与实验数据极大程度吻合[34-35].后文直接使用γ-Reθ转捩模型,代指部署于Chant 2.0 平台的横流拓展γ-Reθ转捩模型.
本文运用γ-Reθ转捩模型对横流转捩模态下间歇因子γ的数值与分布进行计算,并对DNN 进行监督学习,构建从层流流场物理量到转捩流场间歇因子γ间的映射关系,从而得到一种新的数据驱动转捩模型.仅需将数据驱动转捩模型与SSTk-ω湍流模型耦合,即可对横流不稳定性主导的边界层转捩进行预测,简化计算过程.
本文采用数据驱动转捩模型与湍流模型耦合求解的手段,研究了人工智能转捩计算方法对横流转捩的预测能力,以期为今后的人工智能算法与CFD耦合工作提供方法参考.
1 模型构建
1.1 DNN 监督学习框架
本文参照γ-Reθ转捩模型求解间歇因子γ,修正SSTk-ω模型湍动能k输运方程的生成项与耗散项,进而实现转捩预测的思路,利用DNN 构建来流条件、壁面信息和流场结构等物理信息与间歇因子γ间的映射关系,用新的数据驱动转捩模型替代γ-Reθ转捩模型,实现人工智能建模框架下的三维边界层横流转捩的高效准确预测.
目前已有许多基于层流解的边界层转捩研究工作[36-39].以本文所用的γ-Reθ转捩模型构造为例,在发生转捩前流场处于全层流状态,通过迭代层流流场的物理量从而开启横流源项DSCF实现转捩预测,即层流流场中存在能够用于判断横流转捩起始位置的点.因此本文选择使用层流流场物理量映射转捩流场间歇因子,训练数据的具体获取方式如下.首先对层流状态进行计算,快速得到收敛稳定的层流流场,并提取训练所需的物理量.再通过SSTk-ω湍流模型与γ-Reθ转捩模型计算转捩流场,提取各个流场点对应的γ值.将γ与上一步提取的层流流场物理量进行匹配,用于监督学习.DNN 通过梯度下降法,计算γ预测值与监督学习的γ真实值(即γ-Reθ转捩模型计算得到的γ值)之间的损失函数,并对DNN各节点的超参数进行修正,使损失函数降低至设定值以下,从而获得能够满足转捩计算精度要求的映射关系,该映射关系即为本研究的数据驱动转捩模型.DNN 监督学习功能实现的具体过程见图1.
1.2 湍流与转捩模型
本文以RANS 方程对变雷诺数、变后掠角的NFL(2)-0415 后掠翼以及6 : 1 标准椭球体进行求解,采用两方程的剪切应力输运SSTk-ω湍流模型,并与γ-Reθ转捩模型耦合.γ-Reθ转捩模型由间歇因子γ输运方程、转捩动量厚度雷诺数输运方程构成,具体构造如下
横流转捩源项的常系数CCF参照文献[35]的研究结果取0.2,其余常系数、参数与文献[34]保持一致.
γ-Reθ模型与SSTk-ω湍流模型的耦合,通过有效间歇因子γeff对湍动能k方程生成项和耗散项修正实现.SSTk-ω湍流模型的湍动能k方程被修改为
SSTk-ω湍流模型中的融合函数F1也需要修改
式中,Pk,Dk和Florig均为SSTk-ω湍流模型的原始形式[40].
1.3 模型计算能力验证
本文利用γ-Reθ转捩模型对间歇因子γ进行计算,并将计算结果作为γ真实值进行监督学习,参与DNN 训练与测试.得到的数据驱动转捩模型与SSTk-ω湍流模型耦合,用于预测变后掠角的NFL(2)-0415 后掠翼、6 : 1 标准椭球体的三维边界层横流转捩.首先需要对γ-Reθ模型性能进行校验,以证明其计算结果的可靠性.
NFL(2)-0415 后掠翼在−4°攻角(attract of angle,AoA)、45°后掠角(sweep angle,Λ)下[41],上翼面的转捩由横流不稳定性主导,是低速横流转捩典型算例[42].选取该算例,运用γ-Reθ转捩模型对变雷诺数的NFL(2)-0415 后掠翼上翼面转捩位置进行预测,并将计算所得的γ分布与层流流场物理量进行匹配,参与DNN 的训练、测试.具体计算工况见表1.

表1 NFL(2)-0415 后掠翼计算条件Table 1 Conditions of NFL(2)-0415 airfoil
如图2 所示,C 型结构化网格流向i共有400 网格点,其中上、下翼面、上、下尾迹各分布100 网格点,网格法向j共有151 网格点,第1 层网格法向间距y+<1,网格展向k为二层网格,网格数量为120 800.计算采用周期边界条件,以实现无线展长后掠翼的数值模拟.网格在边界层内及边界层附近保证了良好的正交性,粗黑曲线与壁面间的网格点数据用于神经网络的训练.

图2 NLF(2)-0415 后掠翼计算网格Fig.2 Computing mesh for NLF(2)-0415 airfoil
本文采用层流区域与转捩区域Cf曲线延长线交点的无量纲化坐标x/c作为转捩位置xtr,如图3所示.图4 给出了本研究γ-Reθ转捩模型的计算结果与实验结果[41]、langtry-menter-CFH 模型[42]计算结果对比.
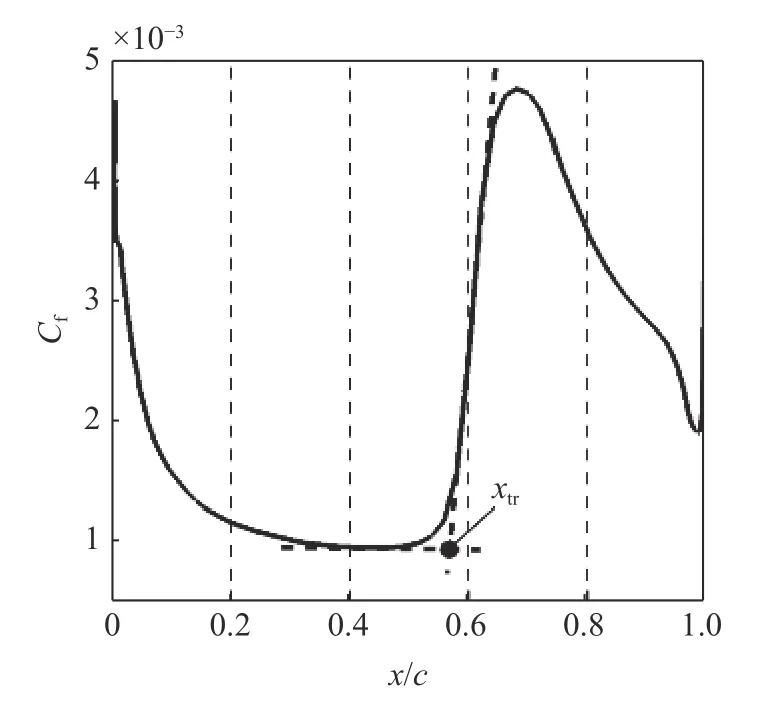
图3 转捩位置判定Fig.3 Determination of transition location

图4 转捩位置对比Fig.4 Comparison of transition location
由图4 可知,γ-Reθ转捩模型计算转捩位置xtr在各工况下均小幅度先于Langtry-Menter-CFH 模型.γ-Reθ转捩模型在低雷诺数下,计算转捩位置xtr相较于实验结果略微提前,随着雷诺数增大,计算转捩位置xtr逐渐与实验结果贴近,最后几乎重合.Langtry-Menter-CFH 模型在低雷诺数下计算转捩位置xtr同样存在略微提前的问题,随着雷诺数增大,计算转捩位置xtr出现滞后,雷诺数继续增大,计算转捩位置xtr逐渐与实验结果贴近并重合.
转捩模型计算结果与实验结果间的差异,与模型本身构建、模型中部分参数的标定等诸多因素有关,且不同研究中转捩点坐标xtr的判定方式同样存在区别.尽管存在以上影响,γ-Reθ转捩模型计算结果依然能与实验数据吻合较好,与Langtry-Menter-CFH 模型具有相仿的计算性能,能够满足预测精度和DNN 训练的需求.
2 深度神经网络
2.1 深度神经网络超参数
DNN 的输入层为选定的层流流场物理量,并用γ-Reθ模型计算得到的间歇因子γ进行监督学习.输入层单个样本的特征量为V[0]=(v1,v2,v3,···,vn),经过隐藏层时,在神经元节点经历线性变换与激活函数的非线性变化,并将输出值作为下一隐藏层的输入,直至输出最终结果,如图5 所示.其中上角标[j]表示第j个隐藏层,下角标i表示该隐藏层的第i个神经节点.

图5 深度神经网络正向传播Fig.5 Positive propagation of DNN
训练样本集中的单个样本首先经过如下线性变换与非线性变换
经测试,在本研究中选取sigmoid 函数作为激活函数学习效果比ReLU 函数、tanh 函数更佳.非线性变换过程中的激活函数σ选取sigmoid 函数,函数曲线如图6 所示,定义如下
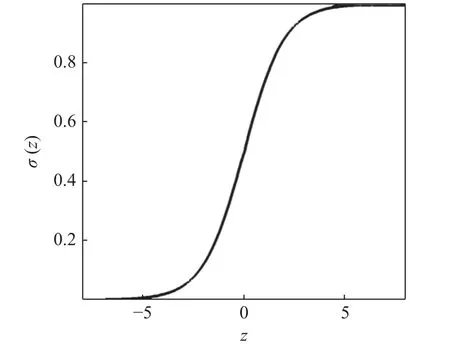
图6 Sigmoid 函数Fig.6 Activation function of sigmoid
对于共有m个样本的数据集,损失函数定义如下
通过梯度下降法,对神经网络的超参数进行修正,使得损失函数L降低至设定值以下,从而实现神经网络的自主学习过程.
权重W修正如下
阈值b修正如下
其中函数f与Adam 优化器有关,在数据梯度较小的场景以较大的学习率进行更新,在数据梯度较大的场景以较小的学习率进行更新,比标准的SGD算法更有效地收敛.设置默认学习率α=0.001,ε=1 × 10−10.
根据多次训练结果分析,当隐藏层层数等于输入层变量个数,每层神经元节点数等于输入层变量个数3 倍时,能获得较好的训练效果.本文共选取7 个输入变量,故DNN 隐藏层取7 层,每层均设置21 个神经元节点,输出层为单一变量γpredict.
2.2 深度神经网络训练
本文DNN 训练基于Pytorch 平台,构建了层流流场物理量与间歇因子γ间的映射关系,目的在于实现数据驱动转捩模型对三维流场横流转捩的精确预测.输入层7 个变量V=R,Ωstreamwise),各变量定义如下.
用于寻找间歇因子在流向上增长位置的流向雷诺数
如图7 所示,以NLF(2)-0415 后掠翼为例,特征距离s是翼型前缘点A到指定点B,壁面曲线的长度积分,点B处壁面法线L上所有点特征距离s与点B相同.将壁面曲线AB按照网格划分进行离散,点A作为第1 个离散点,点B作为第n个离散点,特征距离s如下

图7 特征距离s 计算Fig.7 Calculation method of characteristic length s
用于寻找间歇因子在壁面法向上增长位置的无量纲壁面法向距离y+[34](通过程序Y+wall distance est imation 计算)
用于寻找间歇因子在壁面法向上增长位置的无量纲化的合速度
用于在流场结构层面确定间歇因子增长位置、无量纲速度对应的应变率张量、旋转率张量的模S,R[34]
在γ-Reθ转捩模型中用于构造无量纲横流强度Hcrossflow、无量纲速度对应的流向涡强度Ωstreamwise[34]
本文D N N 所用的训练数据为4 5°后掠角NLF(2)-0415 后掠翼层流状态的计算数据,以γ-Reθ转捩模型计算得到的间歇因子γ进行监督学习.前文已经给出45°后掠角下5 种不同雷诺数工况,并对γ-Reθ转捩模型计算的准确性进行了校验.对于CFD 计算结果而言,影响占比较大的是边界层内以及边界层附近的间歇因子γ分布情况,因此每种雷诺数下,取上翼面近壁面处i·j=101 × 81=8181 个网格点的数据用作训练以及测试,如图8 所示,即图中白色边线范围内网格点的计算数据,由速度分布可知,该区域包含了上翼面全部边界层.

图8 训练数据所处区域Fig.8 The zone of data for DNN
2.3 深度神经网络拟合校验
随着隐藏层层数以及隐藏层节点数的增加,神经网络的学习能力增强,容易过度挖掘训练样本中特有的映射关系,并将其视为普适性规律,亦或是在已经挖掘出恰当映射关系后,进一步学习并拟合噪音样本,从而导致训练得到的DNN 泛化能力差,出现过拟合现象.现采用5 折交叉验证的方法,以确保本研究训练的DNN 没有发生过拟合,5 折交叉验证方法如图9 所示.
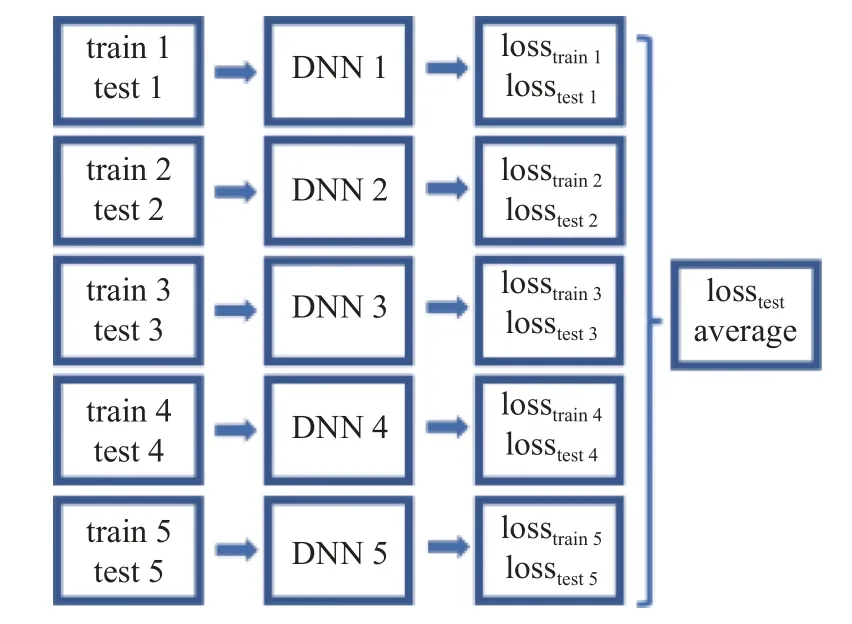
图9 5 折交叉验证Fig.9 5-fold cross validation
5 种工况下共提取了40905 个数据样本,随机均匀划分为5 组,每组包含8181 个数据样本.依次将每组数据样本作为测试集,余下的4 组数据样本作为训练集,训练得到DNN1~ DNN5,并计算训练集、测试集的损失函数以及测试集损失函数的均值.5 折交叉验证的结果见表2.

表2 交叉验证结果Table 2 Result of cross validation
由于测试集中的数据样本没有参与DNN 训练,且DNN 必然存在对特有映射关系的构建以及对训练集噪音样本的学习,交叉验证中测试集损失函数高于训练集是完全合理的.测试集损失函数、损失函数均值均维持在较低的水平,且与训练集损失函数间的差异远未到跨越一个或多个量级的程度,说明DNN 并没有发生过拟合,能够较为精准地预测间歇因子γ的分布.
3 算例分析
3.1 变雷诺数NLF(2)-0415 后掠翼测试
将NLF(2)-0415 后掠翼Re=2.37 × 106以外的其他4 种工况共32724 个数据样本作为训练集,对DNN 进行训练.损失函数设置为7.50 × 10−3,完成30000步训练后,深度神经网络模型实际损失函数为2.0 ×10−4,将其作为本研究算例分析所用的数据驱动转捩模型.以数据样本是否参与DNN 训练作为内插与外推的判别标准,分别用Re=2.73 × 106,Re=2.37 ×106工况下的上翼面近壁区域数据样本对数据驱动转捩模型进行内插与外推测试.图10 给出了两种工况下数据驱动转捩模型对间歇因子预测值与γ-Reθ转捩模型计算值的对比.

图10 间歇因子预测值与计算值对比Fig.10 Comparison between predicted value and calculated value of intermittency
间歇因子预测值与计算值间误差越低,散点分布越接近线性函数y=x.以此为评判标准,两种工况下数据驱动转捩模型对间歇因子的预测均取得了较好的效果.由于没有参与DNN 训练,用作外推测试的工况Re=2.37 × 106间歇因子预测结果在线性函数y=x附近离散程度较高,这与第2.3 节中测试集损失函数高于训练集损失函数的原因一致.由图10 可知,两种工况下近壁区域间歇因子散点,均较为均匀地分布在线性函数y=x两侧,说明两种工况下间歇因子预测值虽然存在不同程度的离散,但与计算值变化规律基本一致,具有良好的预测效果.
运用数据驱动转捩模型对Re=2.73 × 106,Re=2.37 × 106工况下全流场的间歇因子γ进行预测,并与SSTk-ω湍流模型耦合,计算NLF(2)-0415 后掠翼上翼面横流转捩.定义Δγ为数据驱动转捩模型间歇因子预测值减去γ-Reθ转捩模型间歇因子计算值,用于表征数据驱动转捩模型计算结果在空间分布上相较于γ-Reθ转捩模型的偏差.图11给出了上翼面近壁区域Δγ的空间分布.
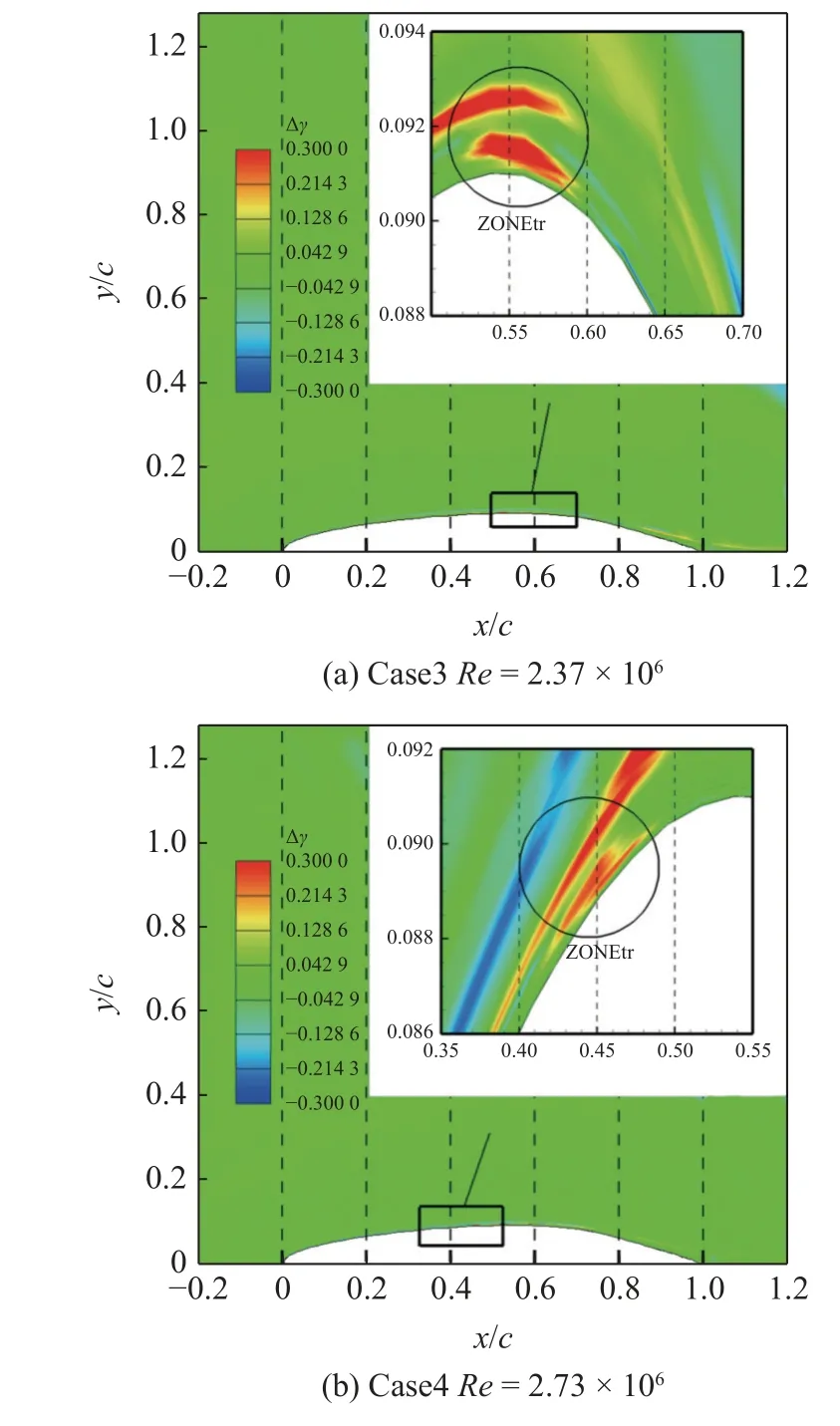
图11 近壁区域Δγ 分布Fig.11 Distribution of Δγ near the wall
观察图11,在转捩区域(即图11 中ZONEtr)贴近壁面处,少部分网格点Δγ大于0,说明数据驱动转捩模型存在将近壁区域间歇因子低值点预测出高值的问题.其中工况Re=2.37 × 106的数据未参与DNN 训练,数据驱动转捩模型预测出现误差的网格点数量多于工况Re=2.73 × 106.
以上翼面的Cf曲线作为数据驱动转捩模型预测精度的判断标准,两种工况下耦合测试的结果如图12 所示.
由图12 可以看出,两种工况下数据驱动转捩模型计算得到的Cf上翼面分布曲线与γ-Reθ转捩模型计算结果吻合较好,其中数据驱动转捩模型计算的转捩位置略微提前.

图12 数据驱动转捩模型与γ-Reθ 转捩模型Cf 计算结果Fig.12 Cf of data driven transition model and γ-Reθ transition model
对数据驱动转捩模型预测转捩位置出现提前的问题进行分析.由图12 可知,工况Re=2.37 ×106下,外插测试的转捩位置提前幅度偏大.前文已经对间歇因子预测值的误差进行了分析,将近壁区域内少量间歇因子低值点预测出较高的值,会导致涡黏性系数μt的高值区域范围增大,使得μt在网格流向与壁面法向上的增长提前,从而导致预测的转捩位置更为靠前.
以工况Re=2.37 × 106下的NLF(2)-0415 后掠翼转捩预测过程为例,采用CPU 时间作为参照标准,使用本研究的预测方法,层流流场计算2 万步至收敛需要3467 s,数据驱动转捩模型输出间歇因子的时间忽略不计(不足10 s),耦合SST 模型计算5 万步至收敛需要14796 s,共需要计算7 万步,耗时约18000 s;使用γ-Reθ转捩模型与SST 模型耦合计算5 万步至收敛,耗时22660 s.对比可知,本研究提出的转捩预测方法可以节约近20%的CPU 时间,一定程度提高了计算效率.
3.2 变后掠角NLF(2)-0415 后掠翼预测
NLF(2)-0415 后掠翼在后掠角足够小时,边界转捩主要为流向转捩,转捩位置靠近机翼后缘;随着后掠角的增大,边界层横流转捩位置逐渐前移,并在后掠角为55°左右时横流转捩位置最靠近机翼前缘,随后逐渐后移[43].延用图2 的计算网格,保持其他工况不变,运用数据驱动转捩模型预测后掠角为45°~65°,Re=2.73 × 106工况下NLF(2)-0415 后掠翼上翼面的横流转捩过程,上翼面流线如图13 所示.
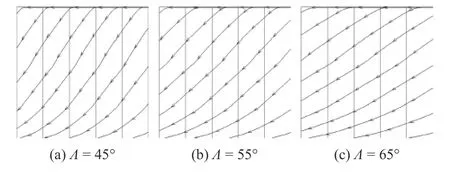
图13 上翼面流线Fig.13 Streamline of upper wing
表3 给出了数据驱动转捩模型与Zlow 平台γ-Reθt-CF-模型对转捩位置的计算结果[43]的对比.

表3 数据驱动转捩模型与γ-Reθt-CF 转捩模型对转捩位置的计算结果对比Table 3 Comparison of xtr between data driven transition model and γ-Reθt-CF transition model
由表3 可知,数据驱动转捩模型在不同后掠角工况下计算得到的转捩位置与γ-Reθt-CF 转捩模型基本一致,证明本研究的数据驱动转捩模型对改变来流条件的横流转捩预测具有一定的泛化能力.
后掠角从45°向65°增大,数据驱动转捩模型计算的转捩位置出现了先向机翼前缘移动,再向机翼后缘移动的现象,其中后掠角55°时转捩位置最为靠前,与文献[43]给出的转捩位置变化规律完全一致.相较于后掠角45°,后掠角65°下转捩位置略微靠前,尽管区别很小,但数据驱动转捩模型依然准确识别了这个细微的差异.
以上分析表明,仅用NLF(2)-0415 后掠翼45°后掠角计算数据训练得到的数据驱动转捩模型能够用于不同后掠角下的横流转捩预测,具备一定的泛化能力,下一步将针对不同外形的横流转捩进行模型测试.
3.3 6 : 1 标准椭球体预测
6 : 1 标准椭球体是典型低速三维转捩标模.在迎角为15°,单位雷诺数为6.5 × 106/m,马赫数为0.136 的工况下,椭球体表面边界层转捩由横流转捩主导[42],具体计算工况见表4.现将数据驱动转捩模型用于预测6 : 1 标准椭球体表面的转捩过程,以进一步校验其泛化能力.

表4 椭球体计算工况Table 4 Conditions of ellipsoid
本文共对椭球体划分3 套计算网格,如图14所示,网格量分别为43 万、180 万和330 万,在保证网格法向j上第1 层网格y+≈3 的前提下,通过改变流向i、法向j、周向k的网格数量、增长率来改变网格总量,分别命名为Mesh A,Mesh B,Mesh C.
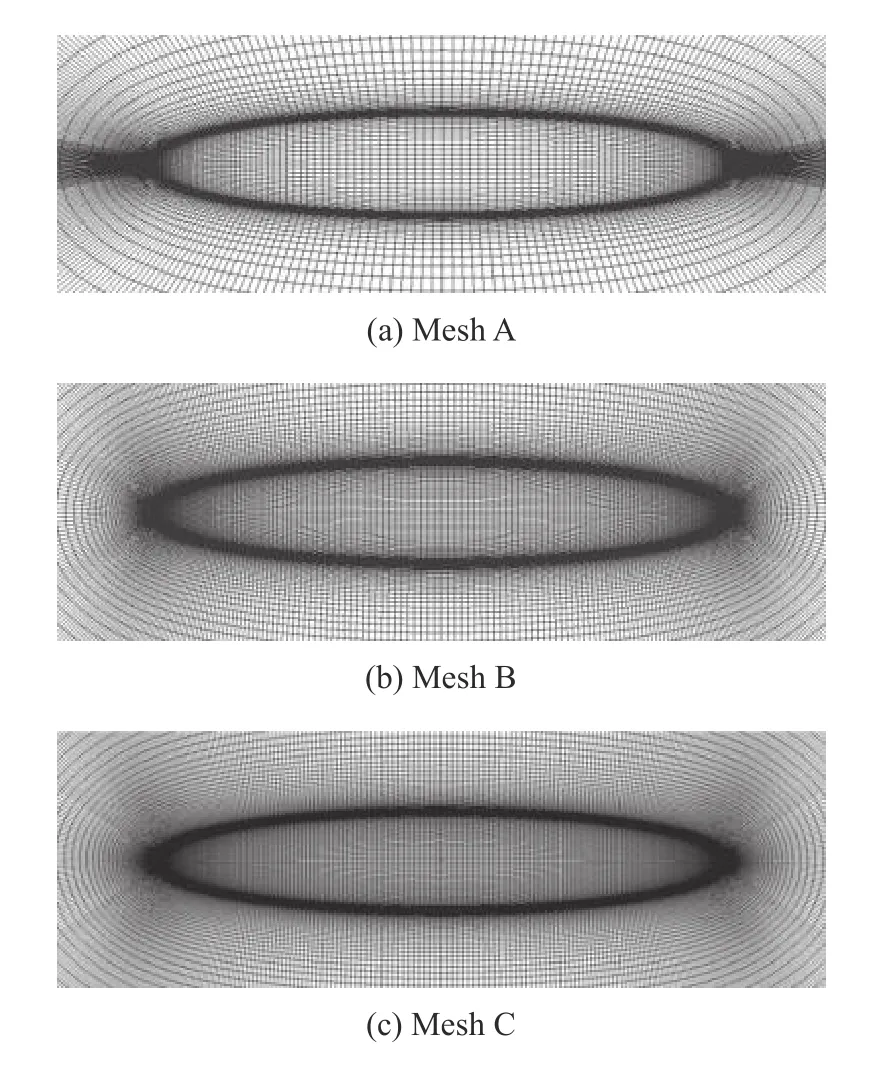
图14 椭球体计算网格Fig.14 Computing mesh for ellipsoid
图15 给出了本文3 套网格下,椭球体上下表面交界线上,层流流场、湍流流场和转捩流场的Cf分布.
由图15 可知,对于层流状态和湍流状态,3 套网格计算得到的Cf分布并无明显差异,但求解γ-Reθ转捩模型后,高分辨率Mesh B,Mesh C 计算得到的Cf分布基本重合,与低分辨率Mesh A 存在较大差异.以上分析表明,对于层流与湍流流场的计算,低分辨率的Mesh A 已经满足网格无关性,但运用γ-Reθ转捩模型求解转捩流场,要求网格分辨率达到Mesh B 以上.由于数据驱动转捩模型输入数据为层流流场物理量,输出量γ直接与湍流模型耦合,因此层流流场与湍流流场计算结果准确与否,对数据驱动转捩模型预测结果影响较大.
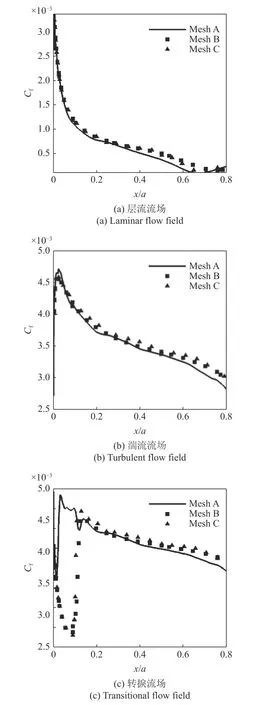
图15 不同流动状态的Cf 分布Fig.15 Cf distribution in different flow states
现采用低分辨率Mesh A 计算层流流场,并提取层流流场物理量输入数据驱动转捩模型,用于预测间歇因子γ.图16 给出了y+≈30 处数据驱动转捩模型预测的间歇因子分布,并与中等分辨率Mesh B 计算的转捩流场间歇因子分布进行对比.
观察图16,数据驱动转捩模型对椭球体迎风面横流转捩的起始位置预测略微提前,但仍具有较高预测精度.在2 次预测出横流转捩后,均发生了不同程度的再层流化.造成这个问题的可能原因如下.
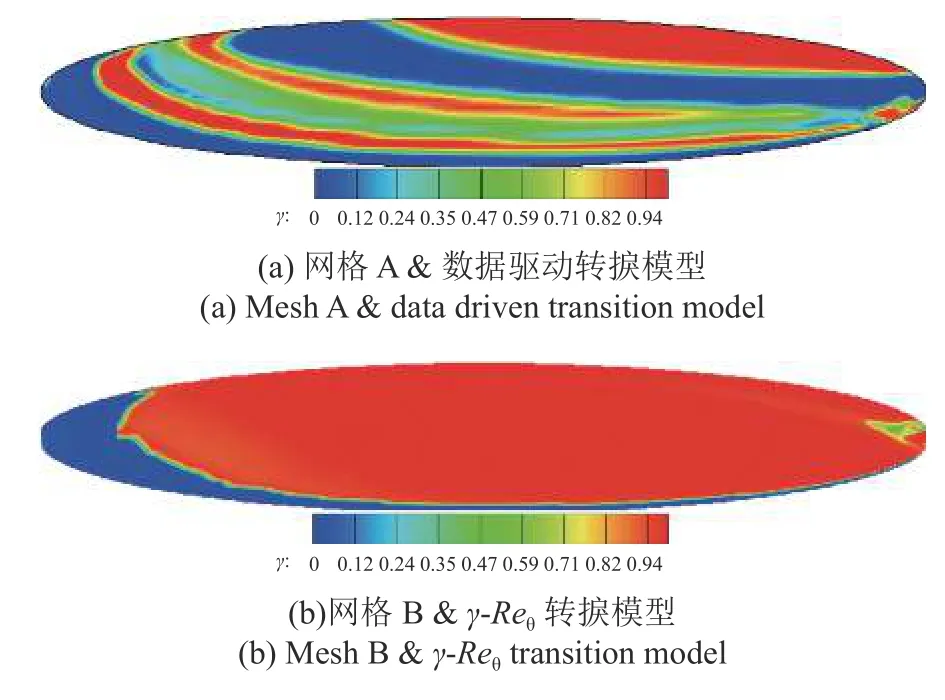
图16 y+≈30 处间歇因子分布Fig.16 Distribution of γ in y+≈30
DNN 仅依靠单一网格点的输入物理量对该点间歇因子进行孤立预测,在预测出大范围转捩后,无法进一步考虑扰动在流向上的传递、叠加,进而修正转捩区域后侧流场间歇因子的预测值.
基于上述推论,本研究对数据驱动转捩模型补充了考虑扰动传递、叠加的算法限制,使其输出的间歇因子预测值在自由来流方向上不会错误地产生衰减,如图17 所示.
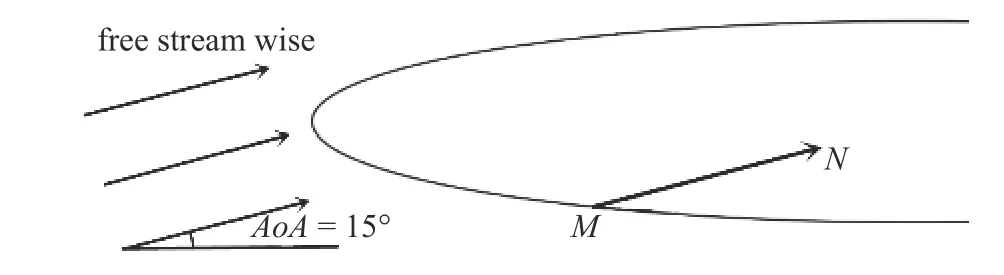
图17 算法限制原理Fig.17 The theory of algorithm
首先利用数据驱动转捩模型对流场中所有网格点的间歇因子γ进行预测.在自由来流方向,即图17中MN指向上,若某网格点的间歇因子γ预测值低于前侧距离最近的网格点,则使用前侧网格点的γ预测值对其重新赋值,从而保证自由来流方向上间歇因子γ预测值始终递增.考虑到椭球体最前端存在少量γ接近1 的高值点,直接启用此算法会导致大量网格点间歇因子被错误地赋为高值,因此算法仅对x/a>0.05 (椭球体长轴a=2.4 m,即x>0.12 m)的网格点预测值进行限制.图18 给出了补充算法限制后y+≈30 处间歇因子预测值.

图18 补充算法限制后间歇因子分布Fig.18 Distribution of γcorrect
补充算法限制后的间歇因子分布与图16(b)基本一致,具有较高的预测精度.继续采用低分辨率Mesh A,将数据驱动转捩模型预测的间歇因子γ以及补充算法限制后的间歇因子γcorrect分别与SSTk-ω湍流模型耦合,计算椭球体表面转捩过程,并与本研究使用的γ-Reθ转捩模型、Chant 平台横流模型[35]、BCDF-CF 代码[34]、OVERFLOW-CF 代码[34]计算结果、实验结果[44]对比,如图19 所示.
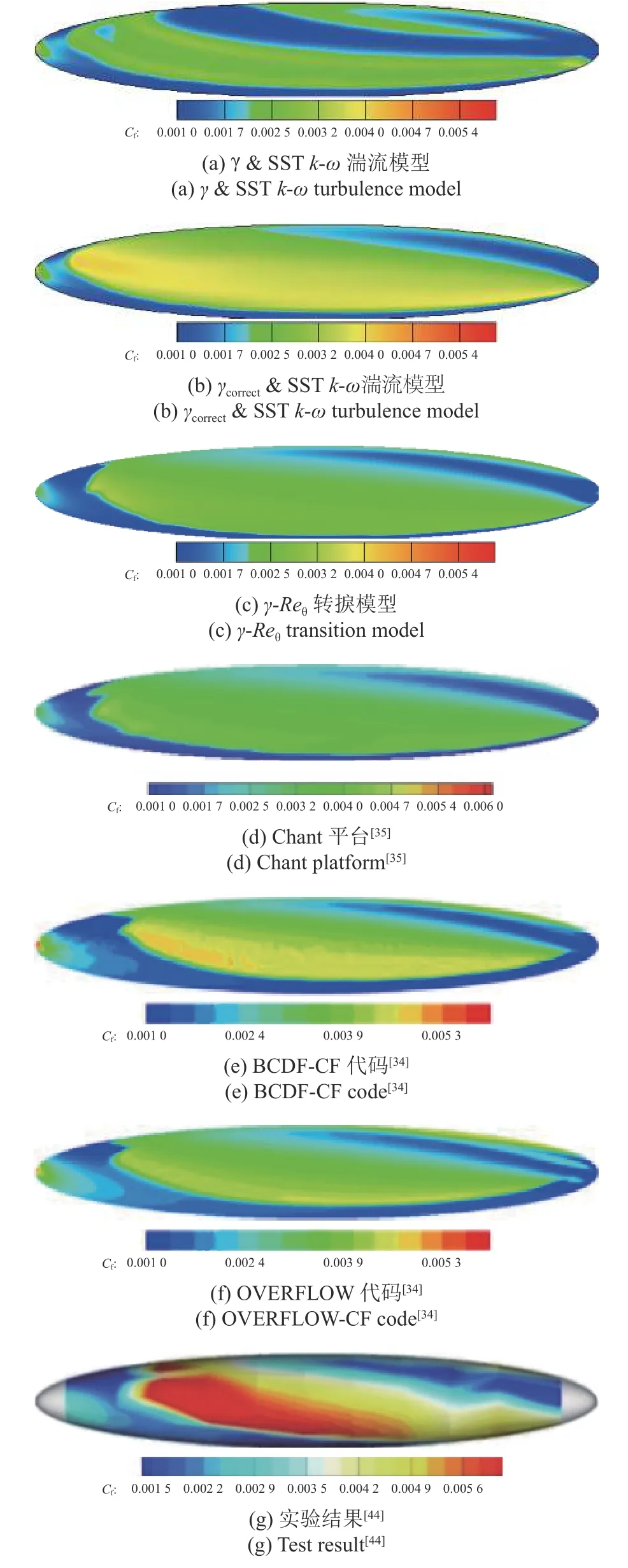
图19 不同算法对Cf 的预测结果以及实验结果Fig.19 Cf of different methods and test
观察图19(a),对数据驱动转捩模型补充限制修正前,椭球体表面Cf分布依然能够反映出转捩阵面的形状,但转捩与湍流区域Cf峰值较低,且第2 次预测出横流转捩后发生的再层流化较为明显.观察图19(b),对数据驱动转捩模型补充算法限制后,对转捩阵面形状的预测能力与本研究使用的γ-Reθ转捩模型、Chant 平台横流转捩模型[35]、Langtry 等[34]给出的两套代码相仿,但在转捩位置预测上依然存在一定程度的提前;层流区域Cf谷值约为0.001,转捩与湍流区域Cf峰值大于0.003,与本研究使用的γ-Reθ转捩模型、Chant 平台横流转捩模型[35]、Langtry等[34]使用的两套代码计算结果基本一致,Cf值均略低于实验结果[44].
以上结果表明,数据驱动转捩模型在显著降低计算成本的同时,具有良好的横流转捩预测能力,实现了对椭球体表面横流转捩的预测.
4 结论
本文运用数据驱动对三维横流转捩进行了预测,结论如下.
(1) 选取层流流场转捩相关物理量对DNN 进行训练,获得的数据驱动转捩模型能够预测变雷诺数的NLF(2)-0415 后掠翼上翼面横流转捩过程,预测转捩位置有小幅度提前,具有较高预测精度.
(2) 由变雷诺数的NLF(2)-0415 后掠翼计算数据训练得到的数据驱动转捩模型具有较好的泛化能力,可以预测变后掠角NLF(2)-0415 后掠翼上翼面的转捩位置,以及椭球体的三维边界层横流转捩.
(3) 数据驱动转捩模型与湍流模型耦合的转捩预测方法,需保证层流、湍流流场的计算精度,在减少整个计算过程所需求解输运方程数量的同时,进一步降低了对网格分辨率的要求,实现高效转捩预测.使用同一套计算网格,相比于γ-Reθ转捩模型,数据驱动转捩模型能够节省近20%的计算时间.
各种因素与边界层转捩间具有复杂的影响机理,如提高粗糙度会导致横流转捩起始位置前移,如流动分离也会引发边界层转捩.针对某个表面粗糙度设计,仅具备较强横流转捩模态识别能力的数据驱动转捩模型,难以完全满足工程应用或科研工作的需求.在下一步工作中,将针对变粗糙度、多转捩模态下间歇因子的预测展开研究工作,尝试在保证数据驱动转捩模型横流转捩预测精度的前提下,实现对包括横流转捩在内的多转捩模态识别,并适用于不同加工精度的表面,提高数据驱动转捩模型的应用范围.
