TA4纯钛带材各向异性屈服行为表征与研究
2023-02-24周兵营豆远航吴向东朱宝辉万敏
周兵营,豆远航,吴向东,朱宝辉,2,万敏
TA4纯钛带材各向异性屈服行为表征与研究
周兵营1,豆远航1,吴向东1,朱宝辉1,2,万敏1
(1.北京航空航天大学 机械工程及自动化学院,北京 100191;2.宁夏中色金航钛业有限公司,宁夏 石嘴山,753000)
基于复杂加载状态试验和先进屈服准则,实现考虑塑性演化的TA4纯钛在复杂加载状态下塑性各向异性行为的精确表征。通过0°、45°、90°方向的单拉试验和复杂加载比例的十字形试件双向拉伸试验,获得TA4纯钛的基本力学性能参数和拉伸屈服轨迹,采用不同的屈服准则对试验屈服轨迹进行预测,并通过变值的屈服准则预测其屈服轨迹的塑性演变规律。在小变形范围内,Yld2000‒2d屈服准则对TA4屈服轨迹的预测精度最高;塑性变形过程中,呈线性增大趋势的值与TA4纯钛的屈服轨迹演变现象直接相关。试验与理论屈服轨迹的对比表明,Yld2000‒2d屈服准则可以实现TA4纯钛初始屈服行为的精确表征。TA4纯钛带材的值随塑性变形呈线性增大趋势,考虑塑性演化的Barlat89屈服准则预测的TA4屈服轨迹外凸性更显著。在TA4纯钛带材冲压成形过程的有限元分析、模具设计和工艺优化中,仅考虑初始屈服轨迹时,可采用Yld2000‒2d屈服准则;当各向异性特征存在较强的塑性演化相关性时,可采用形式相对简单的Barlat89屈服准则。
TA4纯钛;双向拉伸试验;十字形试件;各向异性;屈服准则
钛及钛合金材料凭借优良的力学性能、良好的生物相容性和耐腐蚀性等基本性能,广泛应用于宇航、超导和生物医学等领域[1-2]。随着国内外手机产品的蓬勃发展,钛材料作为一种代表档次升级的新兴材料逐渐被广泛应用于高端手机产品当中,而且其应用潜力巨大,主要体现在高档材质、创新设计、精致工艺等方面。同时,高端手机也朝着功能优化、超薄减重的方向发展,高强TA4纯钛精密薄壁带材正好可以满足这种发展需求,被国内知名企业作为高端新型手机关键部位的首选材料,主要用于替代原高端不锈钢精密带材,实现功能优化、减重和增强舒适感的作用。
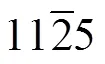
针对材料的各向异性问题,国内外众多学者提出了各种各向异性屈服准则,主要可分为Hill系列、Hosford系列和Drucker系列[8-9]。1948年,Hill等[10]第一次将各向异性的概念引入到von Mises屈服准则中,提出了正交各向异性Hill48屈服准则。Barlat等[11-12]在Hosford各向同性屈服准则的基础上,针对金属材料各向异性行为进行了修改,提出了Barlat89和Yld2000-2d等屈服准则。此外,Cazacu等[13]将各向异性引入偏应力张量不变量中,提出了CPB06等屈服准则,可以更好地描述密排六方金属的屈服行为。为了能更加准确地预测金属板材的屈服行为,越来越多的材料参数被引入到屈服准则当中,综合考虑试验成本、计算开销等各方面因素,目前实际使用较多的屈服准则依然是Mises、Hill48、Barlat89及Yld2000-2d等屈服准则[8]。
有关钛合金屈服行为的研究,国内方面,郭威等[14]采用Barlat89屈服准则研究了钛板试验屈服应力与值之间的定量关系。宋飞等[15]将Hill48和Barlat89屈服准则嵌入Abaqus中,模拟了TA32钛合金马鞍形零件的成型过程,发现Barlat89比Hill48屈服准则具有更高的预测精度。屈聪等[16]基于Mises和Yld2000-2d屈服准则,对Ti-6Al-4V钛合金板材的五点弯曲过程进行了数值模拟,结果表明,Yld2000- 2d模型对钛合金弯曲回弹的预测精度更高。张彦杰等[17]通过试验分析了TA1纯钛极薄带沿不同方向的值对成形性能和壁厚的影响。国外方面,Revil- Baudard等[18]在考虑塑性演化的基础上,对比了Hill48和CPB06屈服准则的预测精度,发现CPB06具有更高的精度,但同时需要更多的试验进行参数标定。Liu等[19]采用Yld2000-2d屈服准则和变弹性模量的方法研究了Ti6Al4V的V形弯曲回弹问题。Ayllon等[20]将Barlat89和CPB06屈服准则扩展到考虑不同温度下拉伸和压缩应力状态下的屈服点,研究了不同温度下Ti6Al4V板的各向异性屈服行为。随着屈服准则的发展,不同系列屈服准则对材料类型的适用性界限越来越不明显,许多准则可以通过优化其中的参数来反映具有不同晶体结构金属板材的屈服行为。与此同时,为了精确表征钛合金的变形历程乃至损伤断裂行为,考虑塑性演化的各向异性屈服准则研究越来越占据重要地位[21-22]。
文中针对0.15 mm厚度的高强TA4精密薄壁带材的各向异性屈服行为进行研究,通过单向拉伸和十字形试件双向拉伸试验,获得TA4纯钛薄壁带材的基本力学性能和初始屈服轨迹。通过对比常见的几种屈服准则对试验屈服轨迹的预测精度,获得最适用于TA4薄壁带材的屈服准则及参数,最后分析值变化趋势与TA4薄壁带材屈服轨迹的演化规律。
1 力学性能试验
1.1 单向拉伸试验
试验材料为宁夏中色金航钛业有限公司提供的厚度为0.15 mm的TA4精密薄壁带卷,化学成分见表1。根据标准GB/T 228.1—2010设计试件形状及尺寸,并采用激光切割加工试件。采用MTS试验机分别对0°、45°、90° 3个方向进行单拉试验,为保证试验为准静态过程,设定单向拉伸速率为2 mm/min,并采用数字图像相关(Digital Image Correlation,DIC)方法获得单拉试件在试验过程中的全场应变,图1a—c分别为MTS多功能试验机、试件加工方向和拉伸断裂后试件的外观和示意图。
表1 TA4的化学成分

Tab.1 Chemical composition of TA4 wt.%
1.2 十字形试件双向拉伸试验
由于TA4精密薄壁带材厚度仅为0.15 mm,为保证试验精度,TA4十字形试件的双向拉伸试验在北航自主建立的多轴同步微尺度双向加载试验系统上进行,如图2所示。双向加载试验系统基于四轴独立驱动的硬件组成和上、下位机分布式控制策略,最大拉力为20 kN,搭配DIC方法测算平面应变,满足位移精度≤0.001 mm、力值精度≤±1%、加载缸同步精度≤±0.01的要求,可用于超薄板带材屈服行为的试验研究[23]。
TA4超薄带材十字形试件尺寸如图3a所示,采用激光切割的加工方式制作。十字形试件双向拉伸试验通常采用载荷控制和应变控制两种方式,由于屈服行为是在应力空间中进行的,因此一般采用载荷控制方式。试验所用十字形试件的2个方向与轧制板材的RD和TD相一致,RD与TD方向的载荷比例分别设为0∶4、1∶4、2∶4、3∶4、4∶4、4∶3、4∶2、4∶1、4∶0。试验速率与单向拉伸试验速率保持一致,为2 mm/min,对应的应变速率约为10‒4s‒1。试验过程中,当试件臂上开缝区发生破裂,载荷曲线下降1 kN(控制载荷),即自动停止试验,图3b所示即为拉伸断裂后的试件。
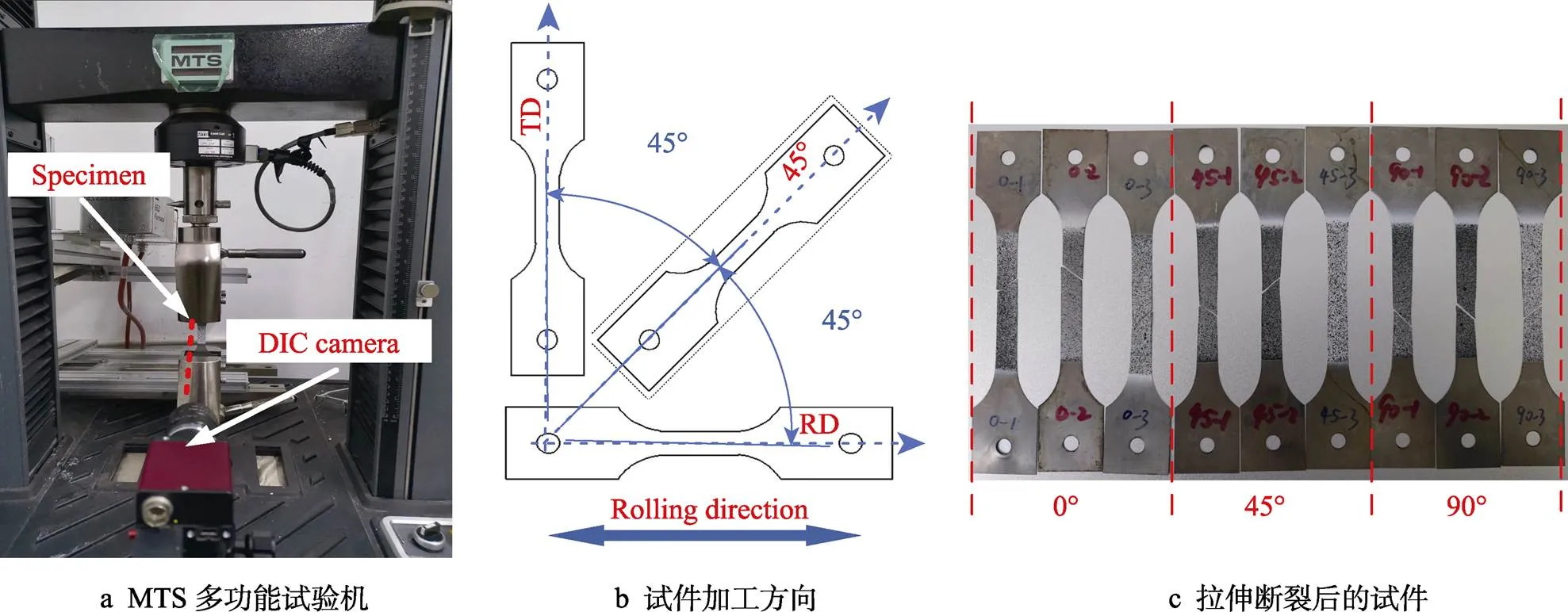
图1 单向拉伸试验

图2 双向加载试验

图3 十字形试件
2 结果与分析
2.1 单向拉伸试验结果
TA4精密薄壁带材的单向拉伸试验结果如图4和表2所示。由图4可知,TA4钛带在3个方向上的各向异性特征非常明显,其中,45°方向的屈服强度最高,90°次之,0°最低;而0°伸长率最大,90°次之,45°相对最小,这与文献[5-7]报道的钛合金薄板在轧制过程中产生的棱锥织构导致钛板材各向异性的情况一致。棱锥织构属于非对称织构,微观层面表现为晶粒在轧制过程中整体上从ND向TD的偏转,宏观层面表现为钛板材在RD的屈服强度低于TD,而伸长率高于TD。

图4 单向拉伸试验应力‒应变曲线
2.2 试验与理论屈服轨迹的对比



Barlat89屈服准则仅适用于平面应力状态,其表达式见式(2)。
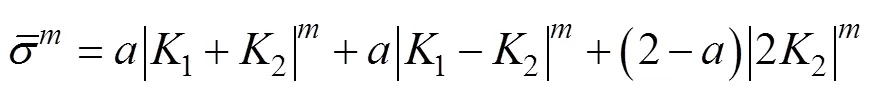
表2 TA4薄壁带材基本力学性能

Tab.2 Basic mechanical properties of TA4 thin-walled strip
Yld2000-2d屈服准则也仅适用于平面应力状态,其表达式见式(3)。
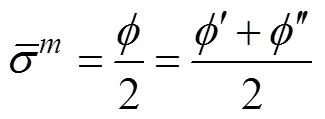
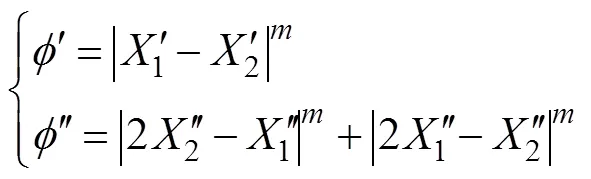

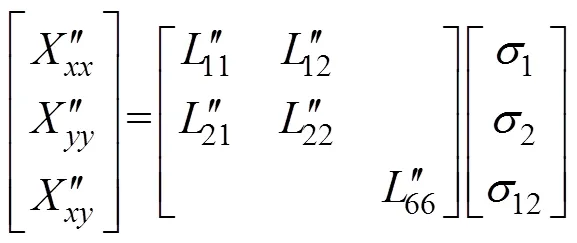
且有如下变换关系,见式(7)。
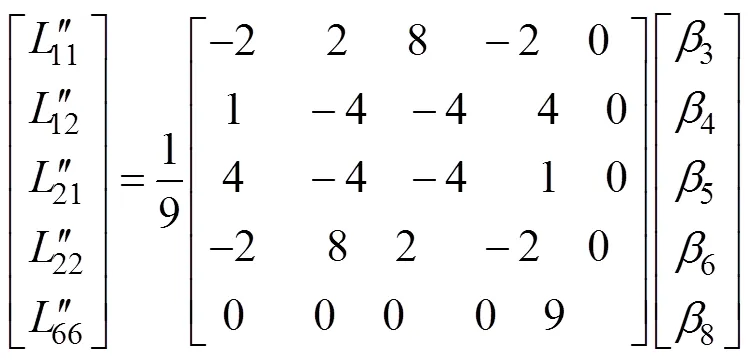
式中:1~8为材料的各向异性参数。
根据单拉试验和不同加载比例的十字形试件双向加载试验得到的应力应变曲线,基于等效塑性功相等原理,计算得到TA4超薄带材在等效塑性应变为0.2%时的试验屈服轨迹,具体计算方法见文献[26]。基于上述试验数据,获得了不同屈服准则的参数,进而获得TA4的理论屈服轨迹。由于Hosford、Barlat89和Yld2000-2d屈服准则均含有非二次各向异性系数,分别取=4、6、8,获得此3种情况下的屈服轨迹并与试验作比较,如图5a—c所示。同时,将Mises、Hill48以及Hosford、Barlat89和Yld2000-2d 3种屈服准则在=8时的情况进行综合比较,如图5d所示。

图5 试验与理论屈服轨迹的对比
为了评估不同屈服准则的精度,引入误差函数,见式(8)。

式中:和分别为试验屈服应力在RD和TD上的应力分量;为试验屈服点与相同加载比例下理论预测屈服点的间距;j为试验屈服点的数量。由式(8)计算不同屈服准则预测试验屈服轨迹的误差柱形图如图6所示。由图6可知,对于Hosford、Barlat89和Yld2000-2d 3个屈服准则,m=8时均表现出相对较高的预测精度,其中,Yld2000-2d屈服准则在m=8时的预测误差为1.32%,表现出最高的预测精度。对于非二次各向异性屈服准则,m的取值与材料的晶体结构有关。由此可得,对于密排六方结构(HCP)材料的屈服轨迹,Yld2000-2d屈服准则在m=8时的预测精度相对最好。Barlat89屈服准则在m=6和8时的预测精度稍差;Mises屈服准则处于中等水平,在预测平面应变和等双拉屈服点时表现出较差的预测精度;Hill48屈服准则的预测精度最差,误差约为4.52%。
2.3 屈服轨迹与r值的关系
采用DIC方法可以获得单向拉伸试验过程中RD和TD方向的真实应变,根据体积不变原理,沿不同方向进行拉伸试验,即可获得TA4超薄带材在0°、45°、90°方向上的值。图7所示为TA4超薄带材3个方向上的值随应变的变化趋势。由图7可知,值在塑性演化过程中变化很大,说明为了更精确地描述TA4超薄带材的塑性行为,建立精确的塑性本构模型,需要在模型中考虑塑性演化现象的影响。在TA4超薄钛带强化阶段,3个方向值的变化趋势近似线性变化,因此可以采用线性拟合的方式进行表征,如式(9)所示。
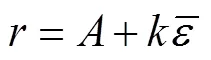
式中:和为拟合参数,如表3所示。
表3 TA4超薄带材值拟合参数
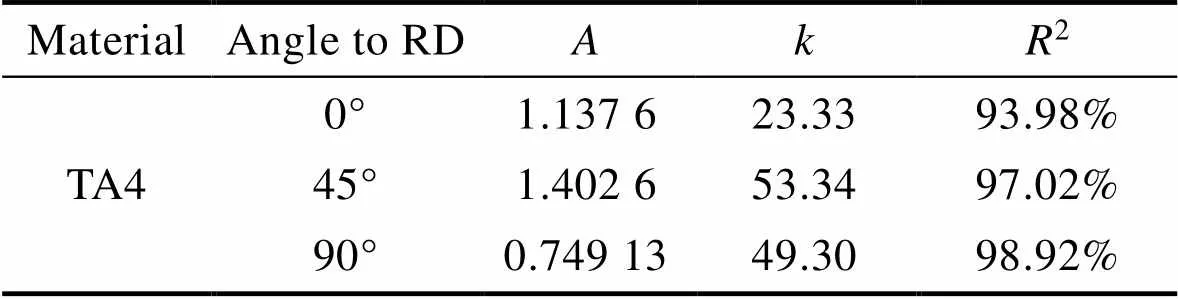
Tab.3 Fitting parameters of r value in TA4 ultra-thin strip
由于本研究所用TA4钛带较薄,双臂开缝的十字形试件中心区获得的塑性应变范围有限,因此无法选择需要等双拉试验条件下大应变数据的Yld2000- 2d屈服准则,而前文表明,Barlat89屈服准则在=8时的预测精度相对较高。由此,在研究TA4超薄钛带的值演化对屈服轨迹的影响时主要采用Barlat89屈服准则,并采用Mises、Hosford进行对照分析。根据获得的值随单向拉伸应变的变化函数,选取塑性应变为0.002、0.02、0.10这3个阶段的值,求解得到的屈服轨迹如图8所示。由图8可知,TA4超薄钛带的值随塑性演化线性增大,各个屈服准则预测的屈服轨迹在值较小时的重合度较好,值较大时其差值相对变大。相比Mises各向同性屈服准则,Hosford主要是在比例加载区加强了预测能力,在单向拉伸的情况下与Mises屈服准则相等,而Barlat89则可以更好地预测强各向异性。通过分析Barlat89屈服轨迹的演化情况可知,由于值增大,TA4超薄钛带在等双拉及平面应变等应力状态下表现出更高的屈服强度,尤其是在主应力偏向TD方向的情况下。

图8 理论屈服轨迹的塑性演化
3 结论
根据复杂加载状态下的单向和双向加载试验和不同的屈服准则,实现考虑塑性演化的TA4超薄钛带在复杂加载状态下塑性变形的精确表征,得出以下主要结论。
1)TA4超薄钛带的各向异性特征非常明显,其45°方向屈服强度最高,90°次之,0°最低;0°伸长率最大,90°次之,45°相对最小,与钛合金薄板在轧制过程中产生棱锥织构的影响规律完全一致。
2)采用不同的屈服准则对TA4超薄钛带的试验初始屈服轨迹进行了预测,发现Yld2000-2d屈服准则对TA4屈服轨迹的预测精度最高,可以实现对TA4钛合金屈服行为的精确表征
3)TA4超薄钛带的值随塑性演化呈线性增长的规律,基于此现象,主要采用Mises、Hosford和Barlat89屈服准则分析其屈服轨迹随塑性演化的变化趋势,结果表明,由于值增大,TA4超薄钛带在等双拉及平面应变等应力状态下表现出更高的强度,尤其是在主应力偏向TD方向的情况下。
[1] GEETHA M, SINGH A K, ASOKAMANI R, et al. Ti Based Biomaterials, the Ultimate Choice for Orthopaedic Implants - A Review[J]. Progress in Materials Science, 2009, 54(3): 397-425.
[2] 王松, 廖振华, 刘伟强. 医用钛合金热氧化处理工艺及其耐磨损、耐腐蚀性能和生物活性的研究进展[J]. 中国有色金属学报, 2014, 24(6): 1466-1473.
WANG Song, LIAO Zhen-hua, LIU Wei-qiang. Research Progress on Thermal Oxidation Process and Wear, Corrosion Resistance and Bioactivity of Biomedical Grade Titanium Alloy[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(6): 1466-1473.
[3] KIM W J, YOO S J, LEE J B. Microstructure and Mechanical Properties of Pure Ti Processed by High-Ratio Differential Speed Rolling at Room Temperature[J]. Scripta Materialia, 2010, 62(7): 451-454.
[4] ROTH A, LEBYODKIN M A, LEBEDKINA T A, et al. Mechanisms of Anisotropy of Mechanical Properties of α-Titanium in Tension Conditions[J]. Materials Science and Engineering: A, 2014, 596: 236-243.
[5] ZHU Z S, LIU R Y, YAN M G, et al. Texture Control and the Anisotropy of Mechanical Properties in Titanium Sheet[J]. Journal of Materials Science, 1997, 32(19): 5163-5167.
[6] 余世伦, 张孝军, 孔玢, 等. 退火工艺对冷轧工业纯钛带卷各向异性的影响[J]. 金属热处理, 2022, 47(3): 82-87.
YU Shi-lun, ZHANG Xiao-jun, Kong Bin, et al. Effect of Annealing Process on Mechanical Anisotropy of Cold Rolled Commercial Pure Titanium Coil[J]. Heat Treatment of Metals, 2022, 47(3): 82-87.
[7] 詹从堃, 陈志永, 唐林. 退火纯钛板压缩力学性能的各向异性[J]. 中南大学学报(自然科学版), 2012, 43(11): 4253-4258.
ZHAN Cong-kun, CHEN Zhi-yong, TANG Lin. Anisotropy of Compressive Mechanical Properties of Annealed Pure Titanium Sheet[J]. Journal of Central South University (Science and Technology), 2012, 43(11): 4253-4258.
[8] 万敏, 程诚, 孟宝, 等. 金属板材屈服行为与塑性失稳力学模型在微尺度下的应用[J]. 精密成形工程, 2019, 11(3): 1-13.
WAN Min, CHENG Cheng, MENG Bao, et al. Mechanical Model for Yielding Behaviour and Plastic Instability of Sheet Metals and Its Application at Microscale[J]. Journal of Netshape Forming Engineering, 2019, 11(3): 1-13.
[9] 赵辉, 彭艳, 石宝东. 金属材料各向异性本构模型研究进展[J]. 塑性工程学报, 2022, 29(10): 32-42.
ZHAO Hui, PENG Yan, SHI Bao-dong. Research Progress on Anisotropic Constitutive Model of Metal Materials[J]. Journal of Plasticity Engineering, 2022, 29(10): 32-42.
[10] HILL R, OROWAN E. A Theory of the Yielding and Plastic Flow of Anisotropic Metals[J]. Proceedings of the Royal Society of London Series A Mathematical and Physical Sciences, 1948, 193(1033): 281-297.
[11] BARLAT F, LIAN K. Plastic Behavior and Stretchability of Sheet Metals. Part I: A Yield Function for Orthotropic Sheets under Plane Stress Conditions[J]. International Journal of Plasticity, 1989, 5(1): 51-66.
[12] BARLAT F, BREM J C, YOON J W, et al. Plane Stress Yield Function for Aluminum Alloy Sheets—Part 1: Theory[J]. International Journal of Plasticity, 2003, 19(9): 1297-1319.
[13] CAZACU O, PLUNKETT B, BARLAT F. Orthotropic Yield Criterion for Hexagonal Closed Packed Metals[J]. International Journal of Plasticity, 2006, 22(7): 1171-1194.
[14] 郭威, 周飞, 陈积伟, 等. 用Barlat-Lian屈服准则对钛板实验的研究[J]. 吉林工业大学学报, 1993, 23(1): 36-39.
GUO Wei, ZHOU Fei, CHEN Ji-wei, et al. The Experimental Study of Ti Sheet by Using the F. Barlat-Lian Yield Criterion[J]. Journal of Jilin University of Technology, 1993, 23(1): 36-39.
[15] 宋飞, 王宁, 苏楠, 等. TA32钛合金马鞍形零件热冲压工艺数值模拟[J]. 稀有金属材料与工程, 2022, 51(9): 3252-3262.
SONG Fei, WANG Ning, SU Nan, et al. Numerical Simulation of Hot Stamping Process for Saddle Shape Part of TA32 Titanium Alloy[J]. Rare Metal Materials and Engineering, 2022, 51(9): 3252-3262.
[16] 屈聪, 孟智娟, 赵亮, 等. 基于变弹性模量的Ti-6Al-4V板材五点弯曲回弹预测[J]. 中国机械工程, 2022, 33(16): 1991-1999.
QU Cong, MENG Zhi-juan, ZHAO Liang, et al. Prediction of Five-Point Bending Springback of Ti-6Al-4V Plates Based on Variable Elastic Modulus[J]. China Mechanical Engineering, 2022, 33(16): 1991-1999.
[17] 张彦杰, 李渤渤, 陶会发, 等. 纯钛燃料电池双极板软模成形工艺研究[J]. 精密成形工程, 2022, 14(4): 109-114.
ZHANG Yan-jie, LI Bo-bo, TAO Hui-fa, et al. Soft Mold Forming Process of Pure Titanium Bipolar Plate for Fuel Cell[J]. Journal of Netshape Forming Engineering, 2022, 14(4): 109-114.
[18] REVIL-BAUDARD B, MASSONI E. Simulation of the Anisotropic Behavior of Titanium Alloys during Sheet Metal Forming[J]. International Journal of Material Forming, 2009, 2(1): 73.
[19] LIU Zi-jian, MA Li-dong, MENG Zhi-juan, et al. Effect of Yield Criterion and Variable Elastic Modulus on Springback Prediction of Ti-6Al-4V Sheet V-Shaped Bending[J]. The International Journal of Advanced Manufacturing Technology, 2021, 116(5): 1925-1936.
[20] AYLLÓN J, MIGUEL V, MARTÍNEZ-MARTÍNEZ A. Extended Anisotropy Yield Criteria Applied to Ti6Al4V at a High Range of Temperatures and Considerations on Asymmetric Behavior[J]. Materials & Design, 2021, 208: 109933.
[21] YANG H, LI H, SUN H, et al. Anisotropic Plasticity and Fracture of Alpha Titanium Sheets from Cryogenic to Warm Temperatures[J]. International Journal of Plasticity, 2022, 156: 103348.
[22] KUMAR M A, N’SOUGLO K E, HOSSEINI N, et al. Theoretical Predictions of Dynamic Necking Formability of Ductile Metallic Sheets with Evolving Plastic Anisotropy and Tension-Compression Asymmetry[J]. International Journal of Material Forming, 2022, 15(4): 51.
[23] 熊晶洲, 万敏, 孟宝, 等. 基于多轴同步控制的微尺度双向加载实验系统[J]. 北京航空航天大学学报, 2019, 45(1): 174-182.
XIONG Jing-zhou, WAN Min, MENG Bao, et al. Micro-Scaled Biaxial Loading Test System Based on Multi-Axis Synchronous Control[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(1): 174-182.
[24] 王海波, 万敏, 阎昱, 等. 参数求解方法对屈服准则的各向异性行为描述能力的影响[J]. 机械工程学报, 2013, 49(24): 45-53.
WANG Hai-bo, WAN Min, YAN Yu, et al. Effect of the Solving Method of Parameters on the Description Ability of the Yield Criterion about the Anisotropic Behavior[J]. Journal of Mechanical Engineering, 2013, 49(24): 45-53.
[25] 王海波, 陈正阳, 阎昱. 屈服准则对DP600钢板各向异性行为的预测能力[J]. 塑性工程学报, 2015, 22(2): 45-50.
WANG Hai-bo, CHEN Zheng-yang, YAN Yu. Capabilities of Yield Criteria on Predicting the Anisotropic Behaviors of DP600 Steel Sheet[J]. Journal of Plasticity Engineering, 2015, 22(2): 45-50.
[26] 吴向东. 不同加载路径下各向异性板料塑性变形行为的研究[D]. 北京: 北京航空航天大学, 2004.
WU Xiang-dong. Study on Plastic Deformation Behavior of Anisotropic Sheet Metal under Different Loading Paths[D]. Beijing: Beihang University, 2004.
Characterization and Study on Anisotropic Yield Behavior of TA4 Pure Titanium Strip
ZHOU Bing-ying1, DOU Yuan-hang1, WU Xiang-dong1, ZHU Bao-hui1,2, WAN Min1
(1. School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China; 2. Ningxia Horizontal Titanium Industry Co., Ltd., Ningxia Shizuishan 753000, China)
The work aims to accurately characterize the plastic anisotropic behavior of TA4 pure titanium considering plastic evolution under complex loading state based on complex loading state test and advanced yield criteria. The basic mechanical properties and yield loci of TA4 pure titanium were obtained through uniaxial tension at 0°, 45° and 90° directions and biaxial tension of cruciform specimen with complex loading ratios, and different yield criteria were used to predict the yield loci, and the evolution of yield loci was predicted by the yield criterion with variablevalue. In the small deformation range, Yld2000-2d yield criterion had the highest prediction accuracy for TA4 yield loci. In the plastic deformation process, the linear increasing trend ofvalue was directly related to the evolution of the yield loci of TA4 pure titanium.The comparison between experimental and theoretical yield loci shows that Yld2000-2d yield criterion can accurately characterize the initial yield behavior of TA4 pure titanium. Thevalue of TA4 pure titanium strip increases linearly with plastic deformation, and the outer convexity of TA4 yield loci predicted by Barlat89 yield criterion considering plastic evolution is more significant. In the finite element analysis, die design and process optimization of TA4 pure titanium strip stamping process, Yld2000-2d yield criterion can be used when only the initial yield loci is considered. Barlat89 yield criterion with relatively simple form can be used when anisotropic characteristics have strong plastic evolutionary correlation.
TA4pure titanium; biaxial tension test; cruciform specimen; anisotropy; yield criterion
10.3969/j.issn.1674-6457.2023.02.002
TG389
A
1674-6457(2023)02-0011-08
2022‒10‒27
2022-10-27
宁夏回族自治区重点研发计划(2021BFH02003);中国有色集团科技计划(2021KJJH04)
Key R&D Program of Ningxia Hui Autonomous Region (2021BFH02003); Science and Technology Program of China Nonferrous Metal Group (2021KJJH04)
周兵营(1994—),男,博士生,主要研究方向为塑性成形理论与有限元分析。
ZHOU Bing-ying (1994-), Male, Doctoral candidate, Research focus: plastic forming theory and finite element analysis.
吴向东(1970—),男,博士,副教授,主要研究方向为先进板材塑性成形理论与工艺。
WU Xiang-dong (1970-), Male, Doctor, Associate professor, Research focus: advanced plastic forming theory and technology.
周兵营,豆远航,吴向东, 等. TA4纯钛带材各向异性屈服行为表征与研究[J]. 精密成形工程, 2023, 15(2): 11-18.
ZHOU Bing-ying, DOU Yuan-hang, WU Xiang-dong, et al. Characterization and Study on Anisotropic Yield Behavior of TA4 Pure Titanium Strip[J]. Journal of Netshape Forming Engineering, 2023, 15(2): 11-18.
