基于BCU-Tree与字典的高效用挖掘快速脱敏算法

尹春勇，李 荧

（南京信息工程大学 计算机与软件学院，南京 210044）

0 引言

数据挖掘［1］旨在从结构化或非结构化的数据中提取有用信息，并将其结构化以供人们使用。近年来，频繁模式挖掘（Frequent Pattern Mining，FPM）［2］、关联规则挖掘（Association Rule Mining，ARM）［3］、频繁事件挖掘（Frequent Episode Mining，FEM）［4］和序列模式挖掘（Sequential Pattern Mining，SPM）［5］受到研究者们的广泛关注。虽然这些技术被广泛使用，但都忽略了项的效用［6-7］，例如：重要性、兴趣、满意度或风险等。一般来说，效用的隐含信息在生活中很常见。传统的数据挖掘算法往往可能无法挖掘出对用户真正重要的信息。因此，面向高效用模式挖掘（High-Utility Pattern Mining，HUPM）［8］的算法便由此出现。在HUPM 中，每个项的效用可以根据用户的背景知识或者偏好进行预定义。

根据维基百科的介绍，在经济学中，效用就是对某些商品（包括服务，即满足人们需求的东西）偏好的度量，它代表消费者对商品的满意程度。因此，效用是一种主观衡量标准。在实践中，效用的价值是由用户根据他对特定领域知识的理解来分配的，这些知识由特定价值衡量，例如成本、利润或审美价值。兴趣度量可以分为客观度量、主观度量和语义度量［9-11］：客观度量［11-12］仅基于数据本身，例如：模式挖掘中支持度或置信度；而主观度量［13-14］考虑了用户对该领域的认知，例如不了解、新颖；对于语义度量［8］考虑数据本身和用户的期望，例如效用。因此，效用是对用户偏好的定量表示，项集的有用性是根据其效用值来量化的。效用可以定义为衡量一个项集的有用（即有利可图）程度［8，15］。

隐私保护效用挖掘（Privacy Preserving Utility Mining，PPUM）通过结合隐私保护数据挖掘（Privacy Preserving Data Mining，PPDM）和HUPM 来进行隐私保护。可以说PPUM 是PPDM 的一个子领域。隐私和效用是PPUM 中两个相互对立的指标。隐私保护［16］通常使用的两种方法是输入隐私和输出隐私。在效用挖掘前，输入隐私会更改数据库的内容（例如扰动［17-18］、k-匿名性［19］等）。在输出隐私的情况下，数据库的内容不会改变，而是让数据仅供预期的人访问（即安全多方计算［20］）。PPUM 使用了一些效用挖掘和隐私保护的技术，以最大限度地保留效用。

在已发表的绝大多数PPUM［21-26］研究中，隐藏敏感高效用项集（Sensitive High-Utility Itemset，SHUI）的主要思想是通过删除某些事务或减少某些项的内部效用来扰乱原始数据库。Yeh 等［21］首先提出了隐私保护效用挖掘策略，即优先隐藏高效用项（Hiding High Utility Item First，HHUIF）和最大敏感项集冲突优先（Maximum Sensitive Itemsets Conflict First，MSICF）算法。这两种算法在每次迭代中都根据自己的标准修改包含敏感项集的数据库事务，以将SHUI 的效用值降低到阈值以下。然而，这两种算法在大数据集中，运行时间较长。因此，为了加快运行速度，Lin 等［22］提出了最大敏感效用-最大项效用（Maximum Sensitive Utility-MAximum item Utility，MSU-MAU）和最大敏感效用-最小项效用（Maximum Sensitive Utility-Minimum Item Utility，MSU-MIU）算法。该算法采用了投影机制来加速原始数据库脱敏过程，旨在使用最大和最小效用的概念有效删除SHUI 或减少其项的内部效用。Yun 等［23］提出了一种基于树结构的快速扰动算法，即使用树与表结构的快速扰动（Fast Perturbation Using Tree and

Table structures，FPUTT）算法，使用两个表的遍历来减小PPUM 的搜索空间。然而，尽管这些算法可以隐藏SHUI，但它们的运行时间都很长。因此本文提出了基于BCU-Tree 与字典（BCU-Tree and Dictionary，BCUTD）的高效用挖掘快速脱敏算法来解决在隐私保护效用挖掘中运行时间长、搜索空间大和副作用大等问题。

本文的主要贡献有4 点：1）设计了一种新的树结构BCUTree，这种树结构采用了一种新颖的编码模型。该编码模型采用按位运算符来提取新的节点，与传统的FPUTT-tree［23］相比，该树的构建与空间搜索速度更快。2）BCU-Tree 采用了“集合枚举树”来生成敏感频繁项，并储存了每个项的效用值来减少效用计算次数，每个项的效用值只需一次更新，无需重复计算。3）该算法采用类似于字典的方式来保存敏感项集所在的所有事务TID，与FPUTT-tree 相比，能够尽可能快地在BCU-Tree 中找到某个敏感项所在的所有事务TID，而无需对整个BCU-Tree 进行遍历。4）将本文算法与HHUIF、MSICF、MSU-MIU、MSU-MAU、FPUTT 算法进行了广泛、全面的实验分析与对比，其中包括隐私保护性能、各种真实数据集的可扩展性和时间复杂度理论分析。

1 相关工作

1.1 高效用挖掘

近年来，高效用挖掘一直是数据挖掘领域中的一个研究重点。在过去的几十年中，研究者提出了大量针对各种类型数据的高效用挖掘算法，包括交易数据、顺序数据、情节数据和流数据。根据效用挖掘的原理和数据结构的不同，挖掘算法大致可以分为基于Apriori 方法、基于树的方法、基于垂直或水平数据的方法和基于投影的方法。

在基于Apriori 方法中，Shen 等［27］提出了面向目标的基于效用关联（Objective-Oriented utility-based Association，OOA）挖掘算法，该算法提出了一种基于效用约束的新剪枝策略，提高了OOA 挖掘效率；Yao 等［15］在算法中根据效用约束的几个数学特性来寻找高效用项集（High-Utility Itemset，HUI）。总之，早期的所有效用挖掘算法都改进了Apriori 方法。它们的一个共同缺点是都需要生产大量候选项，因此这些改进方法面临计算成本高和内存消耗大等问题。

为了避免基于Apriori 的逐级搜索的缺点，学者们提出了基于树的方法。基于树的效用挖掘算法灵感来自传统的基于树的频繁模式挖掘算法［2］。Hu 等［28］提出了一种用于识别高效用项组合的频繁项集挖掘算法。首先，该算法识别高效用组合，然后通过高收益分区树找到HUI，其目标是找到满足特定条件并最大化预定义目标函数的数据段和项目/规则组合。Ahmed 等［29］提出了三种新的树结构来有效执行增量和交互式高效用模式挖掘。树中的每个节点代表一个项集，并由项集的名称、事务加权利用率（Transaction-Weighted Utilization，TWU）值和支持计数组成。Wu 等［30］提出了两种新的剪枝策略，能避免访问搜索空间中非必要节点；此外，通过多线程来处理大数据集，从而减少算法运行时间。

为了获得比基于树的效用挖掘方法更高的效率，研究者提出了一些使用具有单阶段的垂直或水平数据结构挖掘高效用项集的算法，例如高效用模式挖掘（High-Utility Pattern Miner，HUP-Miner）算法［31］和高效的高效用项集挖掘（EFficient High-utility Itemset Mining，EFIM）算法［32］。除此以外，Gan 等［33］为评估模式在事务数据库中的效用，扩展了占用度量，该算法通过效用、占用率和频率来考虑用户偏好，能够挖掘出高质量项集，并无候选集生成。Wu 等［34］基于Hadoop 框架开发了一种高模糊效用模式挖掘算法，该算法无论是在单机还是大规模环境中都有着杰出的表现。

1.2 隐私保护效用挖掘

效用挖掘的目的主要是挖掘不低于最小效用阈值的高效用项集，并发现用户所感兴趣的信息，但效用挖掘可能会泄露敏感数据。因此，在HUPM 中也存在隐私问题。在一些实际应用中，敏感的高效用模式（项集、序列、情节等）通常需要隐藏。因此，近年来PPUM 成为学者们研究的重点。

数据库中某个项的效用定义为内部效用之和乘以其外部效用。一般来说，降低一个项的效用值有两种方法：1）直接减少项的内部效用值；2）改变外部效用值来降低这个模式的价值。在真实的世界中，外部效用一般是固定的，不会发生变化，因此，减少项的内部效用更为合理。Yeh 等［21］提出了两种新的算法HHUIF 和MSICF，除了隐藏敏感信息外，最大限度地减少了隐藏敏感项带来的副作用。Yun 等［23］引入了一种新的树结构来加快扰动过程，减小PPUM 的搜索空间。Lin 等［22］提出了MSU-MAU 和MSU-MIU 两种算法来最小化在隐藏高效用敏感项集中带来的副作用。Li 等［35］提出了一种基于整数线性规划（Integer Linear Programming，ILP）的新算法来减少隐藏过程中产生的副作用，将隐藏高效用敏感项集过程描述为满足约束条件的问题。Liu 等［24］在脱敏过程中，动态计算每个敏感项的冲突计数，从而选择冲突计数最大的项进行脱敏。Liu 等［25］提出了三种启发式隐私保护算法，即先选择最大效用项、先选择最小效用项和先选择最小副作用项，该算法避免多次扫描数据库，加快了脱敏过程。Jangra 等［26］提出了两种敏感项的选择方法，并通过最小化未命中成本来提高数据效用。

除了隐藏高效用项集，扩展这些算法以处理序列数据也是一项非常重要的任务。受基于项集的HHUIF 和MSICF 算法的启发，Dinh 等［36］首先提出了隐藏高效用顺序模式（Hiding High Utility Sequential Pattern，HHUSP）和最大顺序模式冲突优先（Maximum Sequential Patterns Conflict First，MSPCF）算法来隐藏所有高效序列模式。为了克服HHUSP和MSPCF 的缺点，Quang 等［37］通过效用升序或者降序来减少执行时间和丢失成本，从而提高HHUSP 的性能。Le 等［38］提出了一种新颖结构隐藏效用链（Utility-Chain for Hiding，UCH）来加快脱敏过程，在运行时间、内存消耗和副作用方面有着杰出表现。

2 预备知识

为了更好地理解PPUM，本章介绍一些相关的预备知识，并简要说明PPUM 问题。

2.1 定义

给定一个数据库，表示为D=｛T1，T2，…，Tn｝，其中Tm(1 ≤m≤n) 表示一个事务。每个事务都是由有限个项集I={i1，i2，…，im}组成。例如表1 所示，I={A，B，C，D，E}，由项组成的集合叫作项集。r-项集表示包含r个项，如I={C，E}，叫作2-项集。

表1 一个事务数据库Tab.1 One transaction database

定义1项的内部效用im(1 ≤m≤M)在事务Tn中，用q(im，Tn)表示，含义为Tn中im的数量，例如在表1 中，项C 的内部效用在T2中为2，即q（C，T2）=2。

定义2项的外部效用im用p（im）表示，例如项的重要性、利润、网页链接点击次数。表2 给出了一个外部效用的例子，其中项C 的外部效用为1，即p（C）=1。

表2 项外部效用表Tab.2 External utility table of items

定义3在事务Tn中，项im的效用表示为u（im，Tn），计算公式如下：

其中X⊆Tn，否则u(X，Tn)=0。例如T2中项集AC 的效用根据式（2）计算为u(AC，T2)=u(A，T2)+u(C，T2)=1×5+2 ×1=7。由于事务T3中不含项集AC，则u（AC，T3）=0。

定义5在数据库D中，u（X）表示项集X的效用，计算公式为：

例如，项集AC 的效用在表1 中的效用为u(AC)=u(AC，T2)+u(AC，T5)+u(AC，T7)+u(AC，T8)=1×5+2 ×1+3×5+10×1+6×5+9×1+1×5+2×1=78。

定义6事务Tj在数据库D的效用是事务Tj中所有项im的效用之和，计算公式为：

例如T2在数据库D的效用为tu（T2）=1×5+2×1+2×2=11。

定义7TU表示D中所有事务效用tu（Ti）之和，即数据库总效用，计算公式为：

定义8效用是用来评估项集的重要性或者价值，它是一种直观的度量单位。最小效用阈值是用户用来确定项目集是否有利用价值的标准。用δ来表示最小效用阈值，该阈值为常数，一般由用户自己设置，即δ=c(0 ≤c≤TU)。

定义9高效用项集是指项集X的效用不小于最小效用阈值δ，即IH=｛X⊆I，u（X）≥δ｝，例如假定δ=44 时，u（AC）=78≥44，则AC 为高效用项集。

2.2 问题陈述

一个事务数据库D，有一组集合H满足最小效用阈值的HUI。定 义S=｛S1，S2，…，Sn｝是SHUI 的集合，则集合NS（=H-S）是一组非敏感HUI。PPUM 的目的是隐藏敏感项集S，使S中的每个Sm效用值都小于最小效用阈值δ。主要方法就是修改敏感项集Sm中项的数量值（内部效用）来降低Si的效用，但尽可能地保留NS，从而使隐私保护带来的副作用降到最低。脱敏后的数据库为D'，从D'中挖掘HUI，用H'表示。通常，PPUM 算法的流程为：1）对数据库D应用效用挖掘算法，获取所有的HUI；2）在数据发布前，确定所有的敏感项；3）使用隐私保护算法，来隐藏所有SHUI，并使算法的副作用最小化。PPUM 算法的性能指标用以下方式来衡量。

定义10隐藏失败（Hiding Failure，HF）为脱敏后的数据库中未能隐藏的SHUI，即脱敏过后仍出现在数据库中的SHUI。定义为：

定义11丢失成本（Missing Cost，MC）为缺失的HUI，即不敏感但在脱敏后会隐藏的HUI。定义为：

定义12人工成本（Artificial Cost，AC）为在脱敏过程之前不是HUI，但在脱敏数据库后成为HUI 的项集，这就是H'和H之间的区别。定义为：

3 数据脱敏算法

本文提出的BCUTD 算法的基本思想是保留数据表每行中的SHUI，并通过这些SHUI 建立SI-table，该表存储了高效用敏感项集及该项集所在的所有事务TID。根据所有敏感项集中项出现的次数建立BCU-Tree，并存储该项所在数据表中信息，包括TID、内部效用和外部效用。遍历SI-table，选择最大效用的项，通过字典表查找并更改该项对应BCU-Tree节点的相关信息，使该敏感项集效用低于用户自定义阈值。只需一次遍历BCU-Tree，修改原始数据库中的数据表信息来达到数据库脱敏效果。BCUTD 算法的整个流程如图1所示。

图1 BCUTD算法的整体流程Fig.1 Overall flow of BCUTD algorithm

3.1 构建SI-table和BCU-Tree

作为BCUTD 算法的初始步骤，构建高效用敏感项集表SI-table 和BCU-Tree 查找树结构。数据持有者在共享数据时，第三方可以通过数据挖掘来发现有用信息，然而这些信息可能是敏感的，如果被不信任的第三方获取，则可能造成一定的损失。因此SI-table 用来存储由数据持有者指定的SHUI。为了减少在数据扰动过程中大量扫描数据库，计算项的效用值，建立BCU-Tree 查找树，并生成字典表指向该查找树，来减少扰动的时间和CPU 计算次数。

SI-table 用来保存高效用敏感项集和所在的事务TID，相关定义如下：

定义13设原始数据库D，SHUI 是用户指定的高效用敏感项集。只需扫描数据库D一次，便可创建SI-table，其中每个敏感项集si∈I，SI-table 定义如下：

SI-table 包括两个字段：SI 和TIDs。例如，通过效用挖掘算法，得到表3 所示的高效用项集，指定其中的｛ACD｝、｛BD｝、｛CD｝为高效用敏感项集。

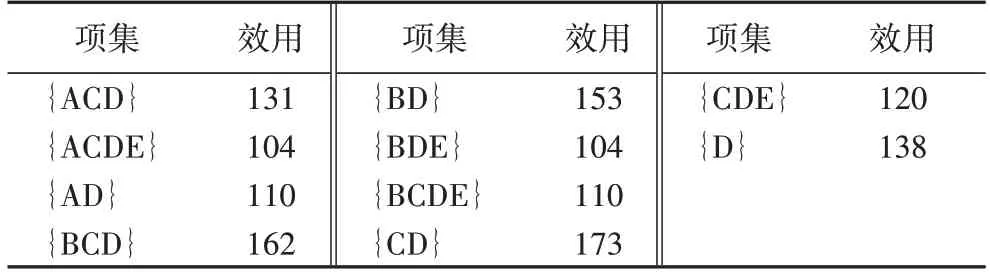
表3 高效用项集Tab.3 High-utility itemsets

通过一次遍历表1 中的事务，建立如表4 所示的SItable。SI-table 用来构建BCU-Tree 及树的扰动。通过SItable，可以减少扫描数据库次数，无需像HHUIF 和MSICF［21］那样，分别处理每个敏感高效用项集。创建SI-table 的算法如算法1 所示。

表4 敏感项集表Tab.4 SI-table

除了构建SI-table 以外，在扫描数据库的同时，构建了BCU-Tree，该树的建立是基于位图编码，其相关定义如下。

定义14设≻关系为∀i1，i2∈F1（敏感项集合），当且仅当num（i2）≥num（i1）时，i2≻i1。其中num表示该项出现的次数。为了简要说明，本文以表1 为例，去除其中的非敏感项，得到了表5 中数据。对表5 中每个敏感项出现的次数进行统计，得到了表6，因此敏感项｛A，B，C，D｝的≻关系为D≻C≻A≻B。

表5 敏感事务表Tab.5 Sensitive transaction table

表6 敏感项计数表Tab.6 Counting table of sensitive items

定义15设L1是有序敏感项零向量，其中项集按对应项的计数num（a）以非降序排序，其中a是一个项。在本研究中，L1表示为L1=[i0，i1，…，inf -1]，其中nf=| |F1（敏感项集合）且inf -1≻… ≻i1≻i0。因此，一个k-项集P表示为Pk=ik…i2i1或Pk=ikPk -1，其中ik≻…≻i2≻i1并且Pk -1=ik -1…i2i1。例如表6 中，F1=｛A，B，C，D｝，L1=｛D，C，A，B｝，一个项集P=｛A，B，C｝可表示为P3=CAB，如图2 所示。

图2 L1向量Fig.2 L1 vector

定义16设Pk=ikPk-1(2 ≤k)，则Pk'表 示Pk'=¬ikPk-1，其中¬ik表示不存在项ik。

定义17∀i∈L1，index表示为i在L1中的索引，图2 展示了表6 中每个项的索引。

定义18BCU-Tree 是一种树，它的结构类似于BMCtree［39］，树结构定义如下：1）它的根节点可以为∅（表示没有项），项前缀子树作为根的子树；2）项前缀子树中的每个节点都持有一个项i(i∈L1)。如果这个节点的父节点代表一个项j，那么j≻i（假设∀i，i∈L1）。到达该节点的路径部分由nodepath 表示；3）每个节点有5 个域：item-name、count、bitmap、children 和UI-list。item-name 表示一个项i(i∈L1)。count 表示包含项i的事务数。bitmap 保存L1（node-path）（定义15）。children 表示该节点的所有孩子节点。UI-list 由Tk、q（i，Tk）和u（i，Tk）组成。每个UI-list 按Tk升序排列，用符号表示为：｛（T1，q（i1，T1），u（i1，T1）），（T2，q（i2，T2），u（i2，T2）），…，（Tk，q(ik，Tk)，u（ik，Tk））｝，如图2 所示。

性质1 BCU-tree 根节点的所有二进制位都是0。

性质2 假设节点N有一个项i1，N.father是N的父节点。则节点N的二进制编码计算如下：

根据定义18 及性质1、性质2，本文构建了BCU-Tree，详细描述见算法2。以表1 为例，其BUC-Tree 的构建结果如图3。除此以外，在文献［23］中，作者构建了FPUTT-tree 树，BCU-Tree 与之相比，构建速度更快，作者使用Header Table来指向FPUTT-tree 节点，在扰动树的过程中，需要多次遍历树，来寻找最大效用敏感项。而本文基于字典的思想，提出了字典表，在扰动的过程中，无需遍历树，只需要查找字典表，找到对应的敏感项，该敏感项指向BUC-Tree 中包含该项的所有节点。以图3 为例，创建的字典表见图4。

图3 BCU-TreeFig.3 BCU-Tree

图4 字典表Fig.4 Dictionary table

字典表由两个域组成，即index（定义17）和bitmap 节点。每个bitmap 节点指向对应BCU-Tree 中的节点编码。例如｛B｝在图3 中的所有节点为1011 和1111。具体算法描述见算法2。

算法2 创建BCU-Tree。

输入 数据库DB；

输出 BCU-Tree（定义18）。

3.2 扰动BCU-Tree

本节详细描述扰动BCU-Tree 的过程。扰动的目的是通过减小SHUI 的内部效用，使它们的效用值低于δ。其中敏感项集按效用值进行降序排列，因为敏感项集的效用越高，它对其他项集的影响就越大。如果优先处理与其他敏感项集重叠的项目较多的某个敏感项集，则后续步骤可以更有效地执行，因为具有更大影响的敏感项集提前降低了稍后处理的敏感项集的效用。

在扰动过程中，无需遍历BCU-Tree，只需要访问字典表，查找到该树中对应的所有节点。在之前的算法中，对数据库采取多次扫描。除此以外，为了解决这个问题，文献［23］中提出了FPUTT-tree 结构，来减少脱敏过程中对数据库的多次扫描。然而，FPUTT-tree 存在一个缺陷，在扰动过程中，需要多次遍历FPUTT-tree，来查找最大效用敏感项，这浪费了很多时间。除此以外，先前的工作需要多次重复计算节点效用值，为了解决这个缺陷，本文提出了新的算法，建立字典表，在扰动的过程中，无需再遍历BCU-Tree，只需查找对应项，便可快速定位到所有节点。每个树节点保存了u（i，Tk）效用值，所有敏感项效用只需计算一次，只有在脱敏的过程中，才需要修改一次效用值。

在算法3 中，首先，将SI-table 中的SI 按照效用进行降序排列（1）行）。遍历每个敏感项集，计算需要减少的总效用（2）～4）行）。遍历敏感项集的每个项，根据图4 字典表选择具有最大效用的项（5）～13）行）。如果最大项效用不大于要减小的效用，将该项的内部效用修改为0；否则根据公式（18）～19）行）计算需要修改的值。

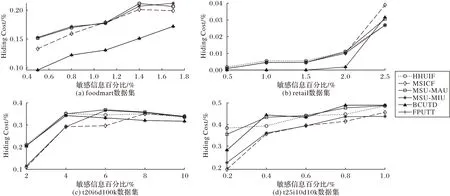
例1 在表3 中，假设专家指定｛ACD｝、｛BD｝、｛CD｝为高效用敏感项集，其中u（ACD）=131，u（BD）=153，u（CD）=173。将这些敏感项集按效用进行降序排列。遍历SI-table 的SI，使每个SI 效用值都小于阈值δ。本文设δ=102，则需要修改的总效用targetUtil=u(CD)-δ=173-102=71。根据字典表（图4）选择｛CD｝最大效用项，按顺序遍历｛CD｝，找到最大效用值，并保存在target中。首先访问C，根据字典表，index=2，定位到0011 节点，根据节点UI-list 中的效用值，可以直接找到C 项的最大效用为（T5，10，10），并保存在target中。接着访问｛CD｝中的D 项，根据字典表，index=3，定位到0001 节点，根据其UI⁃list中的效用值，更新target=D（T4，9，54）。根据算法3（14）～19）行）公式，因为54

图6 扰动后的BCU-TreeFig.6 BCU-Tree after disturbance

算法3 扰动BCU-tree。

输入 SI-table 和δ（定义8）；

输出 扰动后的BCU-Tree。

3.3 BCUTD算法

本节首先介绍修改原始数据库算法（算法4），然后介绍BCUTD 算法的整个流程。与之前相关工作相比，在扰动原始数据库时，无需多次访扫描数据库，只需递归遍历扰动后的BUC-Tree 一次，修改对应节点数据库D 的内部效用值，如算法4 中的描述。在BCUTD 算法中，首先访问原始数据库，建立SI-table 及L1。然后根据3.1 节构建BCU-Tree 和字典表。接着遍历SI-table 的敏感项，根据3.2 节的介绍，扰动BUC-Tree。最后根据算法4，递归遍历扰动后的BUC-Tree，修改原始数据库对应项的效用值。具体算法描述见算法5。

算法4 更新原始数据库DB。

输入 原始数据库DB和BCU-Tree。

输出 脱敏后DB。

4 实验

为了评估BCUTD 算法的性能，本文在多个数据集上进行大量实验。本实验包含4 个数据集，数据集的特征如表7 所示，数据集可从一个开源数据挖掘框架库（http：//www.philippe-fournier-viger.com/spmf/）获得。密度（Density）表示数据集稀密程度，计算公式如下：

表7 实验数据集Tab.7 Experimental datasets

其中：平均长度（AvgLen）表示事务平均长度；Itemcount表示项数量。

除了在不同数据集上进行实验外，本文还与先前算法进行比较，例如：HHUIF 和MSICF［21］、MSU-MAU 和MSU-MIU［40］、FPUTT［23］。在接下来的实验中，本文采用不同的阈值δ和敏感信息在高效用项集中的百分比来进行上述的对比实验。本实验中的敏感项集从HUI 中随机选择，挖掘HUI 算法使用的是ULB-Miner（Utility-List Buffer Miner）［41］。因为实验用的数据集不包含内部效用和外部效用，因此，本实验采用Ge 等［42］提出的均匀分布为事务中每个项分配内部效用值，并采用Tassa［43］提出的高斯分布生成与每个唯一项对应的外部效用。实验在Intel core i7 CPU和16 GB内存的Windows 10环境下运行，所有算法采用Python 3.0编程语言实现。

4.1 运行

本节介绍了六种算法在不同的数据集、不同最小效用阈值和不同敏感信息百分比下的运行效果比较，如图7、8所示。

图7 不同最小效用阈值下的算法运行时间比较Fig.7 Comparison of algorithm running time under different minimum utility thresholds

在图7 中可以看出，随着最小效用阈值的增加，算法的运行时间基本呈下降趋势。因为随着最小效用阈值的增加，则挖掘出来的HUI数量将减少，隐藏相应百分比的SHUI数量将会减少，从而导致算法的运行时间下降。然而，在同一数据集中，当敏感信息百分比相同时，在不同的最小效用阈值下，数据集的SHUI 随机选择。由于不同阈值下的SHUI 随机，每个敏感高效用项集中需要脱敏的项数越多，则算法耗费的时间越长。除此以外，不同的敏感高效用项集所在的事务也有区别。包含该敏感项集的事务数量越多，则算法需要脱敏的时间越长。相反地，如果随机选择的敏感项集项数越少，包含该敏感项集的事务数越少，则算法所耗费的时间越短。正是因为在同一数据集中，随着阈值的改变，SHUI 的随机选择才导致了同一算法的运行时间会随着阈值改变产生波动，但仍然不影响算法的整体趋势。在接下来的实验中，造成算法运行时间及隐藏成本趋势波动的原理基本与此类似。例如图7 中的t20i6d100k 数据集，算法HHUIF、MSICF、MSU-MAU 和MSU-MIU 在阈值分别为0.32、0.33、0.34 时，总体呈上升趋势。产生该现象是因为随机选择的敏感项集中，需要脱敏项集的项数较多，包含该敏感项集的事务数较多，才导致了这些波动。但仍然不影响算法运行时间随着效用阈值的增加而整体下降的趋势。在数据集和最小效用阈值相同的情况下，本文提出的BCUTD 算法要明显优于其他五种算法。与HHUIF、MSICF、MSU-MAU 和MSU-MIU 算法相比，本文算法运行速度提升了2～5 倍。与FPUTT 算法相比，本文算法运行速度提升了0.5～2 倍。在保护效用挖掘的隐私下，不仅要减少隐私保护算法带来的副作用，更要考虑算法的运行时间。在数据集较大的情况下，算法的运行时间与较小的数据集相比，运行时间是它几十倍甚至上百倍。如果因为减少副作用而消耗大量的时间，也是不可取的，由此可见，本文提出的BCUTD 算法的重要性。在图8 中，随着敏感信息百分比的增加，不同算法的运行时间总体呈上升趋势。因为当数据集和最小效用阈值相同时，随着敏感信息百分比的增加，SHUI 数量变多。则算法需要扰动的时间也就越长。在数据集和敏感百分比相同的情况下，BCUTD算法的表现要更为显著。

图8 不同敏感信息百分比下的算法运行时间比较Fig.8 Comparison of algorithm running time under different sensitive information percentages

无论是图7 还是图8，数据集的事务数越少，则算法的运行时间就越少，例如foodmart 和t25i10d10k 数据集。相较于其他两个数据集而言，它们事务数只有几千条，因此运行的时间也相对短一点。从表7 中的数据集密度可以看出，无论数据集密集或稀疏，BCUTD 算法都有良好的可扩展性，运行效果要明显优于其他五种算法。

4.2 副作用

本节介绍了所有算法在副作用方面的实验结果，讨论的副作用包括隐藏失败、丢失成本和人工成本（见3.2 节）。

受进化算法［44］的启发，本文定义了一个具有多个阈值的函数Hiding Cost，来衡量隐私保护中产生副作用的程度。

定义19隐藏成本（Hiding Cost）定义如下：

其中：HF为隐藏失败，MC为丢失成本，AC为人工成本（见3.2 节）；w1、w2、w3是由用户定义的每个副作用的相对权重且w1+w2+w3=1。

本文将六种算法的Hiding Cost 在不同条件下进行对比，实验结果如图9 和图10 所示。

图9 不同最小效用阈值下的算法Hiding Cost比较Fig.9 Comparison of algorithm Hiding Cost under different minimum utility thresholds

图10 不同敏感信息百分比下的算法Hiding Cost比较Fig.10 Comparison of algorithm Hiding Cost under different sensitive information percentages

从图9 可以看出，在不同的最小效用阈值下，相较于其他算法，BCUTD 的副作用相对较小。随着最小效用阈值的上升，所有算法的副作用都随之下降，原因是当数据集和敏感信息百分比相同时，随着最小效用阈值的上升，需要隐藏的SHUI 数量变少，算法的计算复杂度降低，则隐藏成本也会减小。在图10 中，与其他算法相比，BCUTD 在副作用方面仍然有更好的表现。当数据集和最小效用阈值相同时，随着敏感信息百分比的增加，所有算法的Hiding Cost 呈上升趋势，这是因为需要隐藏的敏感信息越多，则算法产生的副作用也会增多。总而言之，本文提出的BCUTD 不仅运行时间更短，产生副作用也更小。

5 结语

近年来，高效用挖掘一直受到商业和工业的追捧。但随着人们隐私意识的提高，高效用挖掘带来潜在的隐私泄露问题引起了研究者们的关注。简要来说，PPUM 就是隐藏敏感高效用项集，当商家共享数据时，其隐藏的敏感信息能不被第三方所挖掘。本文提出了隐私保护效用挖掘算法BCUTD，试图在保护隐私的同时，提高算法的运行效率。本文采用了BCU-Tree 和字典表，来提高脱敏效率。通过大量实验分析和对比，该算法在运行时间和隐私保护副作用上，都有着杰出的表现。在未来的研究中，减少隐私保护效用挖掘的执行时间和内存计算成本，依然是研究者们值得关注的问题。例如：设计新颖的修剪策略，减少搜索空间；开发保证最小副作用的快速近似算法，与启发式算法相结合，求得近似解。